ed36d130ebbc4f95ac205cbfdc508805.ppt
- Количество слайдов: 97

Linear and Non Linear Dimensionality Reduction for Distributed Knowledge Discovery Panagis Magdalinos Supervising Committee: Michalis Vazirgiannis, Emmanuel Yannakoudakis, Yannis Kotidis Athens University of Economics and Business Athens, 31 st of May 2010

Outline o o o Introduction – Motivation Contributions FEDRA: A Fast and Efficient Dimensionality Reduction Algorithm n n o o A Framework for Linear Distributed Dimensionality Reduction Distributed Non Linear Dimensionality Reduction n n o o A new dimensionality reduction algorithm Large scale data mining with FEDRA Distributed Isomap (D-Isomap) Distributed Knowledge Discovery with the use of D-Isomap An Extensible Suite for Dimensionality Reduction Conclusions and Future Research Directions Athens University of Economics and Business Athens, 31 st of May 2010 2/70

Motivation o Top 10 Challenges in Data Mining 1 n n o Typical examples n n n o Banks all around the world Wide Web Network Management More challenges are envisaged in the future n o Scaling Up for High Dimensional Data and High Speed Data Streams Distributed Data Mining Novel distributed applications and trends o Peer-to-peer networks o Sensor networks o Ad-hoc mobile networks o Autonomic Networking Commonality : High dimensional data in massive volumes. 1. Q. Yang and X. Wu: “ 10 Challenging Problems in Data Mining Research”, International Journal of Information Technology & Decision Making, Vol. 5, No. 4, 2006, 597 -604 3/70 Athens University of Economics and Business Athens, 31 st of May 2010

The curses of dimensionality o Curse of dimensionality R 1 2 1 o R 2 22 R 3 23 R 4 24 Empty space phenomenon n Maximum and minimum distance of a dataset tend to be equal as dimensions grow (i. e. , Dmax – Dmin ≈ 0) o Data mining becomes resource intensive n K-means and k-nn are typical examples Athens University of Economics and Business Athens, 31 st of May 2010 4/70

Solutions o Dimensionality reduction n n o The curse of dimensionality n n o MDS, PCA, SVD, Fast. Map, Random Projections… Lower dimensional embeddings while enabling the subsequent addition of new points. Significant reduction in the number of dimensions. We can project from 500 dimensions to 10 while retaining cluster structure. The empty space phenomenon n Meaningful results from distance functions n k-NN classification quality almost doubles when projecting from more than 20000 dimensions to 30. o Computational requirements n Distance based algorithms are significantly accelerated. n k-Means converges to less than 40 seconds while initially required almost 7 minutes. Athens University of Economics and Business Athens, 31 st of May 2010 5/70
Classification q. Problems q. Hard Problems Significant reduction q. Soft Problems Milder requirements q. Visualization Problems q. Methods q. Linear and Non Linear q. Exact and Approximate q. Global and Local q. Data Aware and Data Oblivious Athens University of Economics and Business Athens, 31 st of May 2010 6/70

Quality Assessment q. Distortion: n n Provision of an upper and lower bound to the new pairwise distance. The new distance is provided as a function of the initial distance: n (1/c 1)D(a, b)≤ D’(a, b) ≤ c 2 D(a, b) , c 1, c 2 > 1 n Good method min(c 1 c 2) q. Stress n n n Distortion might be misleading Stress quantifies the distance distortion on a particular example. Stress = √∑(d(Xi, Xj)-d(X’i, X’j))2/∑d(Xi, Xj)2 q. Task Related Metric n n n Clustering/Classification Quality Pruning Power Computational Cost q. Visualization Athens University of Economics and Business Athens, 31 st of May 2010 7/70

Contributions o Definition of a new, global, linear, approximate dimensionality reduction algorithm n n o Definition of a framework for the decentralization of any landmark based dimensionality reduction method n n o Motivated by low memory requirements of landmark based algorithms Applicable in various network topologies Definition of the first distributed, non linear, global approximate dimensionality reduction algorithm n n o Fast and Efficient Dimensionality Reduction Algorithm (FEDRA) Combination of low time and space requirements together with high quality results Decentralized version of Isomap (D-Isomap) Application on knowledge discovery from text collections A prototype enabling the experimentation with dimensionality reduction methods (x-SDR) n Ideal for teaching and research in academia Athens University of Economics and Business Athens, 31 st of May 2010 8/70

FEDRA: A Fast and Efficient Dimensionality Reduction Algorithm Based on : • P. Magdalinos, C. Doulkeridis, M. Vazirgiannis, "FEDRA: A Fast and Efficient Dimensionality Reduction Algorithm", In Proceedings of the SIAM International Conference on Data Mining (SDM'09), Sparks Nevada, USA, May 2009. • P. Magdalinos, C. Doulkeridis, M. Vazirgiannis, "Enhancing Clustering Quality through Landmark Based Dimensionality Reduction ", Accepted with revisions in the Transactions on Knowledge Discovery from Data, Special Issue on Large Scale Data Mining – Theory and Applications. Athens University of Economics and Business Athens, 31 st of May 2010

The general idea o Instead of trying to map the whole dataset in the new space n n n Extract a small fraction of data and embed it in the new space o Create the “kernel” around which the whole dataset is going to be placed Minimize the loss of the information during the first part of the process. Project each remaining point independently by taking into account only the initial set of sampled data. Z Y P 4 P 2 P 1 P 2 Y o o P 3 X X P 3 P 4 The formulation of this idea into a coherent algorithm resulted in the definition of FEDRA (Fast and Efficient Dimensionality Reduction Algorithm) A global, linear, approximate, landmark based method Athens University of Economics and Business Athens, 31 st of May 2010 10/70

Our goal o Formulate a method which combines: n n o Application n o Results of high quality Minimum space requirements Minimum time requirements Scalability in terms of cardinality and dimensionality Hard dimensionality reduction problems o Projecting from 500 dimensions to 10 while retaining interobjects relations o Enabling faster convergence of k-Means Top 10 Challenge: Scaling up for high dimensional data Athens University of Economics and Business Athens, 31 st of May 2010 11/70

The FEDRA Algorithm Input: Output: Projection Dimensionality (k), Original Distances in R n (D), Distance Metric (p) New Dataset in R k (P’) 1. L Select k points and populate set of landmarks 2. L’ Project all landmarks in the target space by requiring that ||L’i – L’j||p = ||Li – Lj||p for 1≤i, j≤k 3. P’ L’ 4. For each of the non landmark points X How do we select landmarks? 4. 1 X’ Obtain the projection of X by requiring that ||L’i – X’||p = ||Li – X||p for 1≤i≤k 4. 2 P’ P’UX’ 5 return P’ Does this system of equations has a solution? Does this simplification come at a cost? Does the algorithm converge? Isn’t it time consuming? These are the questions that we will answer in the next couple of slides Athens University of Economics and Business Athens, 31 st of May 2010 12/70

The theory underlying FEDRA o Theorem 1: A set of k+1 points, pi i=1…k+1, described only by their pairwise distances which have been defined with the use of a Minkowski distance metric p, can be embedded in Rk without distortion. Their coordinates can be derived in polynomial time through the following set of equations: n if j<i-1 then p’i, j is given by the single root of |p’i, j|p - |p’i, j–p’j+1, j|p + ∑f=1 j-1|p’i, f|p-∑f=1 j-1|p’i, f-p’j, f|p + dp(pj+1, pi)p – dp(pi, p 1)p = 0 n if j=i-1 p’i, j =(dp(pi, p 1)p - ∑f=1 i-2|p’i, f|p)1/p n 0 otherwise o Theorem 2: Any equation of the form f(x)=|x|p–|x-a|p–d where aЄR{0}, dЄR, pЄN{0} has a single root in R. o if -1< v=d/|a|p <1 the root lays in (0, a) o otherwise the root lays in (a, |v|a) o The cost of embedding the k landmarks is ck 2/2 where c is the cost of the Newton -Raphson method (for p=2 c=1) Athens University of Economics and Business Athens, 31 st of May 2010 13/70

Theorem 1 in practice (1/2) Z Z Z P 3 P 1 P 2 X o o Y P 1 X Y ||Pi’ Pj’||(p)= P 2 X Y No distortion requires that ||Pi - Pj||(p), i, j=1. . 4 First point is mapped as P’ 1 = O = {0, 0, 0} Second point is mapped at P’ 2 = {||P 2 – P 1||(p), 0, 0} Third points should satisfy simultaneously ||P’ 3 – P’ 1||(p)= ||P 3– P 1||(p) ||P’ 3 – P’ 2||(p)= ||P 3– P 2||(p) The solution is the intersection of the circles Athens University of Economics and Business Athens, 31 st of May 2010 14/70
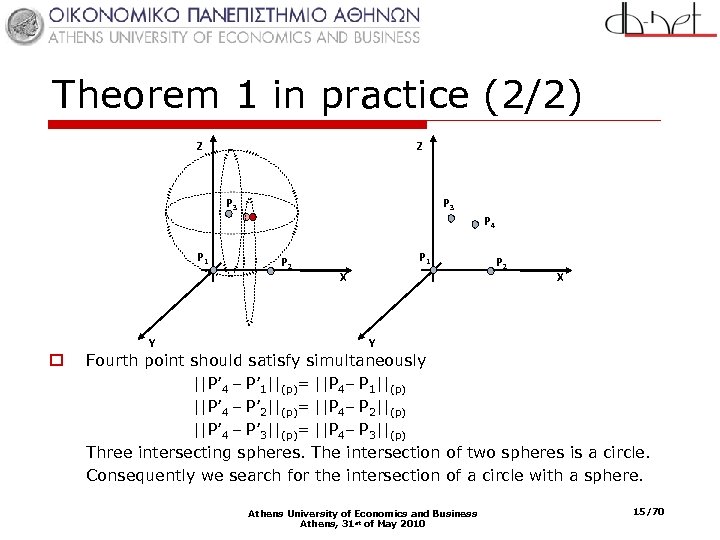
Theorem 1 in practice (2/2) Z Z P 3 P 4 P 1 Y o P 2 P 1 X P 2 X Y Fourth point should satisfy simultaneously ||P’ 4 – P’ 1||(p)= ||P 4– P 1||(p) ||P’ 4 – P’ 2||(p)= ||P 4– P 2||(p) ||P’ 4 – P’ 3||(p)= ||P 4– P 3||(p) Three intersecting spheres. The intersection of two spheres is a circle. Consequently we search for the intersection of a circle with a sphere. Athens University of Economics and Business Athens, 31 st of May 2010 15/70

Reducing Time Complexity (1/2) o Simplified through the following iterative scheme n The embedding of Xi in Rk given the embeddings of Pj , j = 1. . i-1 |x’i, 1|p + |x’i, 2|p + |x’i, 3|p +…. + |x’i, i-1|p = ||P 1 - Xi||p |x’i, 1 -p’ 2, 1|p + |x’i, 2|p + |x’i, 3|p +…. + |x’i, i-1|p = ||P 2 - Xi||p |x’i, 1 -p’ 3, 1|p + |x’i, 2 -p’ 3, 2|p + |x’i, 3|p +…. + |x’i, i-1|p = ||P 3 - Xi||p ……………………………………………. |x’i, 1 -pi-1, 1|p + |x’i, 2 -pi-1, 2|p + |x’i, 3 -pi-1, 3|p +…. + |x’i, i-1|p = ||Pi-1 - Xi||p n Note that by subtracting the second equation from the first we derive |x’i, 1|p - |x’i, 1 -p’ 2, 1|p - ||P 1 - Xi||p + ||P 2 - Xi||p=0 The equation has a single unknown and a single root x’i, 1 n In general, the value of the i-th coordinate is derived by subtracting the (i+1)-th equation from the first. Athens University of Economics and Business Athens, 31 st of May 2010 16/70

Reducing Time Complexity (2/2) q. By subtracting the i-th equation from the first we essentially calculate the corresponding coordinate (i. e. a plane in R 3). q. The intersection of the k-1 planes corresponds to a line. q. The first equation is satisfied by points P 1, P 2 that correspond to the intersection of the line with the norm-sphere of R 3. Z Z Z Y=b X=a O O O X P 1 X X P 2 X=a & Y=b Y Y O(ck 2) Y X=a & Y=b q. We lower time complexity from to O(ck) or even O(k) when p=2 q. What if the intersection of the line with the sphere does not exist? Athens University of Economics and Business Athens, 31 st of May 2010 17/70
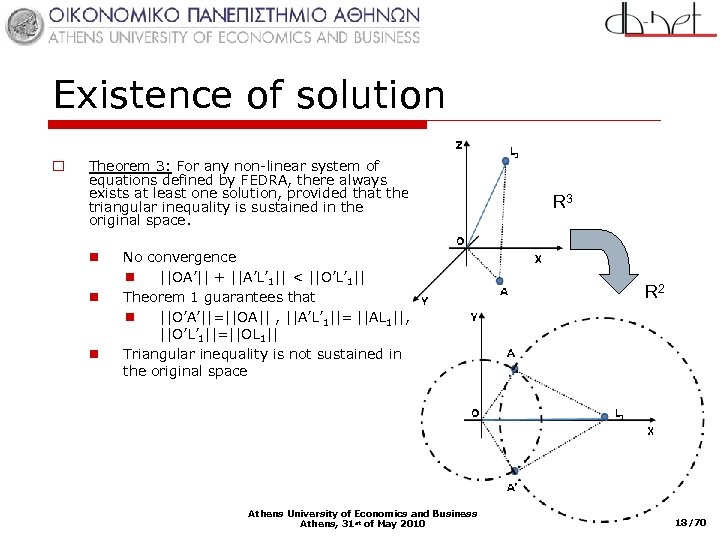
Existence of solution o Theorem 3: For any non-linear system of equations defined by FEDRA, there always exists at least one solution, provided that the triangular inequality is sustained in the original space. n n n No convergence n ||OA’|| + ||A’L’ 1|| < ||O’L’ 1|| Theorem 1 guarantees that n ||O’A’||=||OA|| , ||A’L’ 1||= ||AL 1||, ||O’L’ 1||=||OL 1|| Triangular inequality is not sustained in the original space Athens University of Economics and Business Athens, 31 st of May 2010 R 3 X R 2 18/70

The FEDRA Algorithm Input: Output: Projection Dimensionality (k), Original Distances in R n (D), Distance Metric (p) New Dataset in R k (P’) 1. L Select k points and populate set of landmarks 2. L’ Project all landmarks in the target space by applying Theorem 1 and its accompanying methodology 3. P’ L’ 4. For each of the non landmark points X How do we select landmarks? 4. 1 X’ Obtain the projection of X by applying Theorem 1 and its accompanying methodology 4. 2 P’ P’UX’ 5 return P’ Does this system of equations has a solution? Yes, always! Does this simplification come at a cost? Does the algorithm converge? Yes, always! Isn’t it time consuming? No! In fact it is only O(k) per point! Still some questions remain… Athens University of Economics and Business Athens, 31 st of May 2010 19/70

FEDRA requirements q. FEDRA requirements in terms of time and space q q Exhibits low memory requirements combined with low computational complexity q Memory: O(k 2), k: lower dimensionality q Time: O(cdk), d: number of objects, c: constant q Addition of new point : O(ck) Achieved by relaxing the original requirements and requesting that every projected point retains unaltered k distances to other data points q. Advantageous features q q Operates on similarity/dissimilarity matrix Applicable with any Minkowski distance metric q FEDRA can provide a mapping from Lnp to Lkp where p≥ 1 Athens University of Economics and Business Athens, 31 st of May 2010 20/70
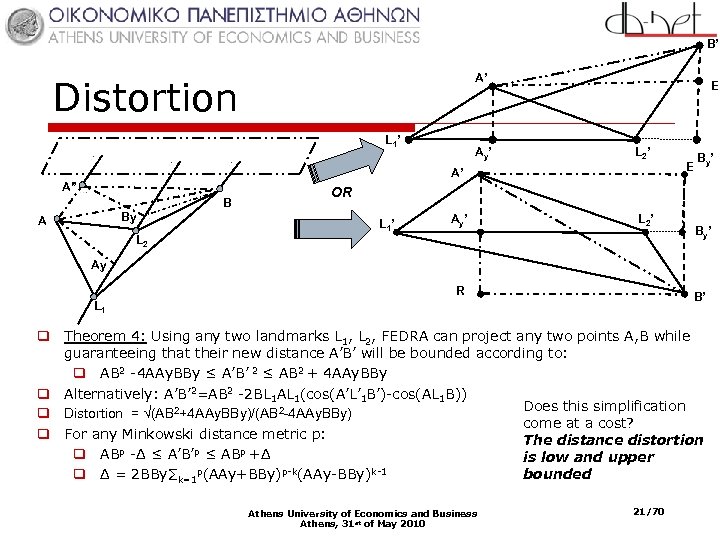
B’ A’ Distortion L 1’ Ay’ E L 2’ E A’ A” B By A By’ OR L 1’ Ay’ L 2 By’ Ay R B’ L 1 q Theorem 4: Using any two landmarks L 1, L 2, FEDRA can project any two points A, B while guaranteeing that their new distance A’B’ will be bounded according to: q AB 2 -4 AAy. BBy ≤ A’B’ 2 ≤ AB 2 + 4 AAy. BBy q Alternatively: A’B’ 2=AB 2 -2 BL 1 AL 1(cos(A’L’ 1 B’)-cos(AL 1 B)) Does this simplification q Distortion = √(AB 2+4 AAy. BBy)/(AB 2 -4 AAy. BBy) come at a cost? q For any Minkowski distance metric p: The distance distortion q ABp -Δ ≤ A’B’p ≤ ABp +Δ is low and upper p(AAy+BBy)p-k(AAy-BBy)k-1 bounded q Δ = 2 BBy∑k=1 Athens University of Economics and Business Athens, 31 st of May 2010 21/70

Landmarks selection o Based on the former analysis it can be proved that the ideal landmark set should satisfy for any two landmarks Li, Lj and any point A, one of the following relations: n Li. A ≈ Lj. A – Li. Lj (or simply that Li. Lj ≈ 0 ) n Lj. A ≈ Li. Lj – Li. A o Li. A ≈ Lj. A – Li. Lj requires the creation of a compact “kernel” where landmarks exhibit minimum distances from each other L 1 C A o L 2 Lj. A ≈ Li. Lj – Li. A requires that cluster centroids are chosen as the landmarks L 1 L 2 So if random selection is not acceptable we use a set of k landmarks that exhibit minimum distance from each other. How do we select landmarks? : Either randomly or heuristically according to theory. o o A Athens University of Economics and Business Athens, 31 st of May 2010 22/70

Ameliorating projection quality (I) q. Depending on the properties of the selected landmarks set, a -single- case of failure may rise 1 Y Z L 2 Y Cluster A Clusters A and B Cluster A Cluster B O O X Y 1. L 1 O L 1 L 2 X Cluster B V. Athitsos, J. Alon, S. Sclaroff, G. Kollios, “Boost. Map: An Embedding Method for Efficient Nearest Neighbor Retrieval”, IEEE Transactions on PAMI, Vol 30, No. 1 January 2008 Athens University of Economics and Business Athens, 31 st of May 2010 23/70
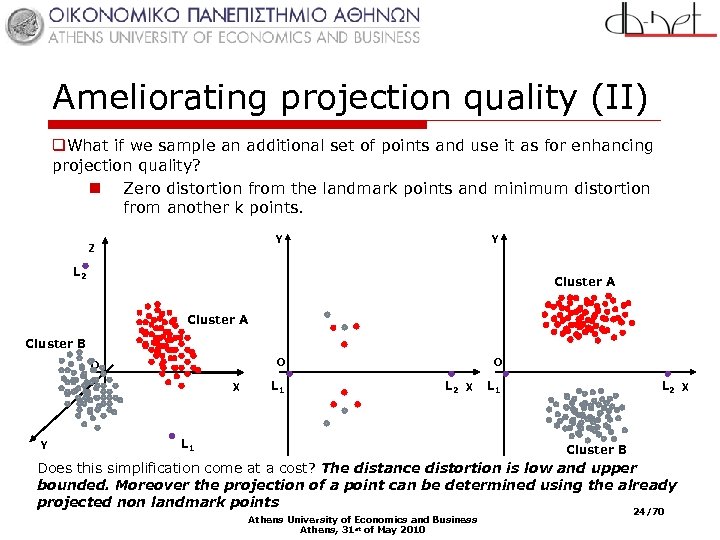
Ameliorating projection quality (II) q. What if we sample an additional set of points and use it as for enhancing projection quality? n Zero distortion from the landmark points and minimum distortion from another k points. Y Z Y L 2 Cluster A Cluster B X Y O O O L 1 L 2 X Cluster B Does this simplification come at a cost? The distance distortion is low and upper bounded. Moreover the projection of a point can be determined using the already projected non landmark points Athens University of Economics and Business Athens, 31 st of May 2010 24/70
FEDRA Applications q. The purpose of the conducted experimental evaluation process is: q Highlight the efficiency and effectiveness of FEDRA on hard dimensionality reduction problems q Highlight FEDRA’s scaling ability and applicability in large scale data mining q Showcase the enhancement of a typical data mining task like clustering due to the application of FEDRA Dataset Cardinality n Classes k Description Ionosphere 351 34 2 3: 1: 7 Radar Observations Segmentation 2100 19 7 3: 1: 7 Image Segmentation Data Musk 476 166 2 3: 3: 15 Molecules Data Synthetic Control 600 60 6 3: 1: 7 Synthetic Dataset Alpha 500000 500 2 10: 50 Pascal Large Scale Challenge ‘ 08 Beta 500000 500 2 10: 50 Pascal Large Scale Challenge ‘ 08 Gamma 500000 500 2 10: 50 Pascal Large Scale Challenge ‘ 08 Delta 500000 500 2 10: 50 Pascal Large Scale Challenge ‘ 08 Athens University of Economics and Business Athens, 31 st of May 2010 25/70

Metrics q. We assess the quality of FEDRA through the following metrics q Stress q √∑(d(Xi, Xj)-d(X’i, X’j))2/∑d(Xi, Xj)2 q Clustering quality maintenance defined as Quality in Rk/ Quality in Rn q Clustering quality: Purity = (1/N) ∑i, j=1 amax(|Ci∩Sj|) q Time requirements for each algorithm to produce the embedding q Time requirements for k-Means to converge q We q q q compare FEDRA with Landmark-based Methods Landmark MDS Metric Map Vantage Objects q As well as prominent methods such as q PCA q Fast. Map q Random Projection Athens University of Economics and Business Athens, 31 st of May 2010 26/70
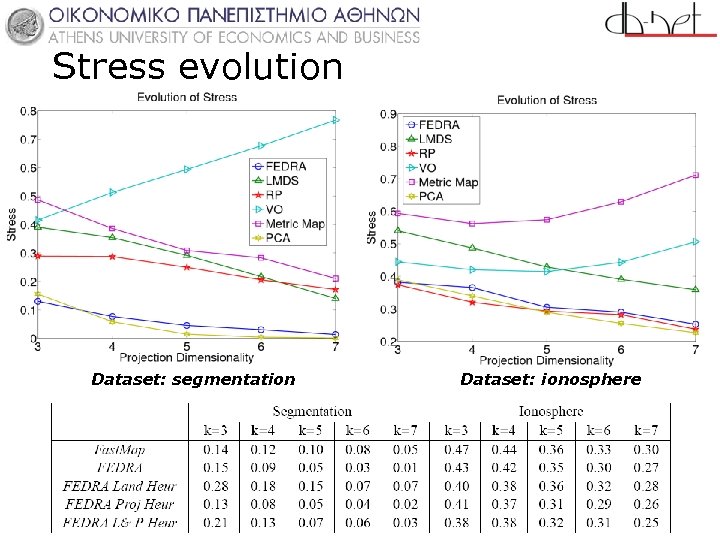
Stress evolution Dataset: segmentation Dataset: ionosphere 27 /81
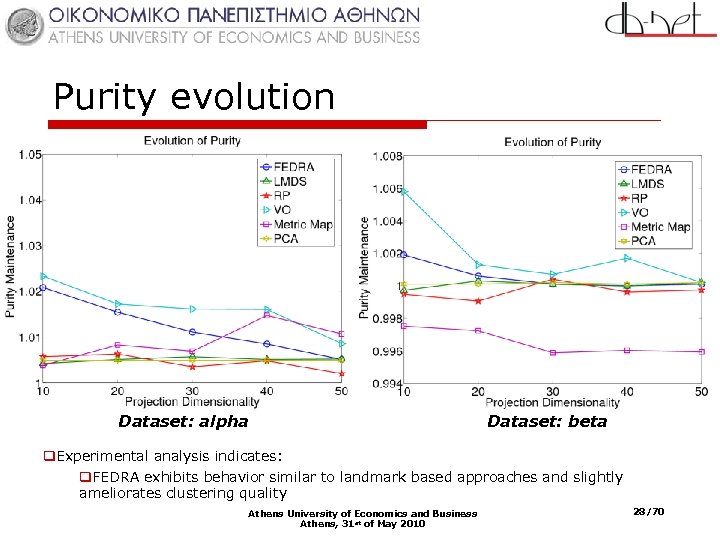
Purity evolution Dataset: alpha Dataset: beta q. Experimental analysis indicates: q. FEDRA exhibits behavior similar to landmark based approaches and slightly ameliorates clustering quality Athens University of Economics and Business Athens, 31 st of May 2010 28/70
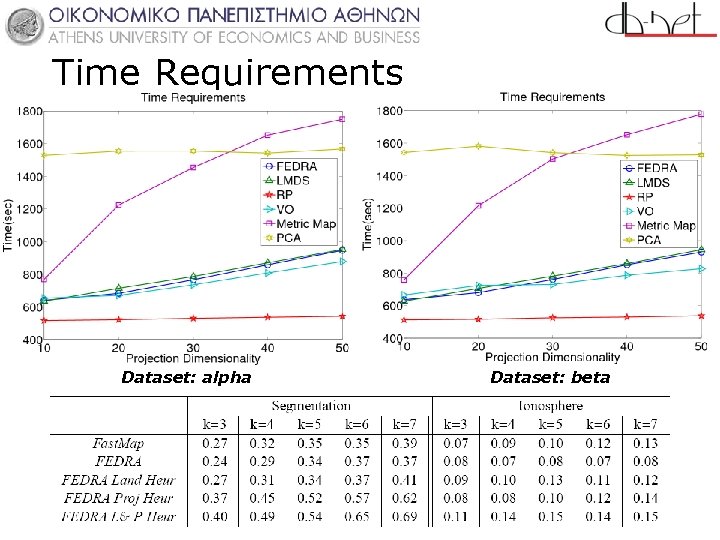
Time Requirements Dataset: alpha Dataset: beta 29 /81
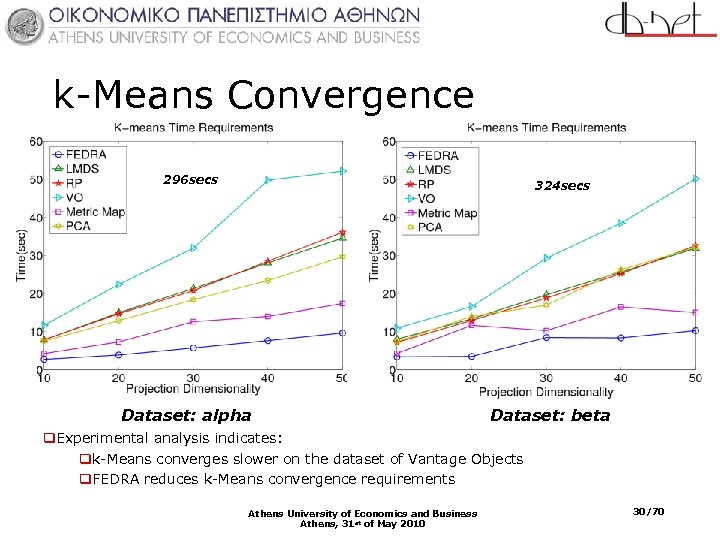
k-Means Convergence 296 secs 324 secs Dataset: alpha Dataset: beta q. Experimental analysis indicates: qk-Means converges slower on the dataset of Vantage Objects q. FEDRA reduces k-Means convergence requirements Athens University of Economics and Business Athens, 31 st of May 2010 30/70

Summary q. FEDRA is a viable solution for hard dimensionality reduction problems. q. Quality of results comparable to PCA q. Low time requirements, outperformed by Random Projection q. Low stress values, sometimes lower than Fast. Map q. Maintain or ameliorate original clustering quality, similar behavior to other methods q. Enables faster convergence of k-Means Athens University of Economics and Business Athens, 31 st of May 2010 31/70

Linear Distributed Dimensionality Reduction Based on : • P. Magdalinos, C. Doulkeridis, M. Vazirgiannis "K-Landmarks: Distributed Dimensionality Reduction for Clustering Quality Maintenance" In Proceedings of 10 th European Conference on Principles and Practice of Knowledge Discovery in Databases (PKDD'06), Berlin, Germany, September 2006. (Acceptance Rate (full papers) 8, 8%) • P. Magdalinos, C. Doulkeridis, M. Vazirgiannis, "Enhancing Clustering Quality through Landmark Based Dimensionality Reduction ", Accepted with revisions in the Transactions on Knowledge Discovery from Data, Special Issue on Large Scale Data Mining – Theory and Applications. Athens University of Economics and Business Athens, 31 st of May 2010
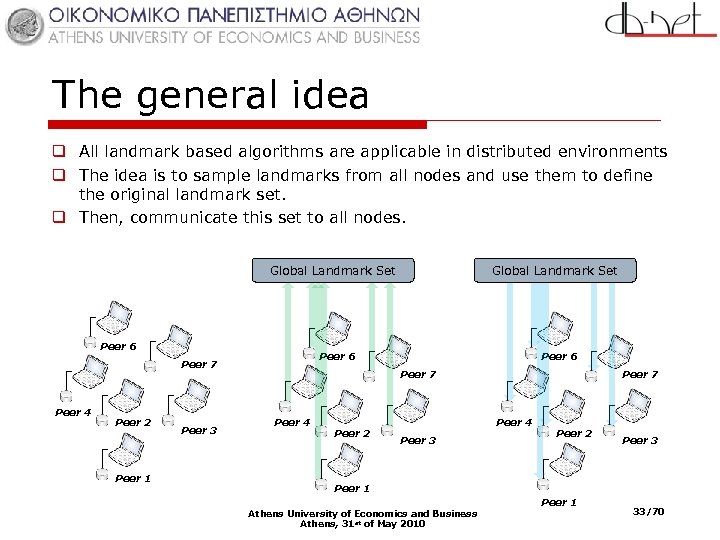
The general idea q All landmark based algorithms are applicable in distributed environments q The idea is to sample landmarks from all nodes and use them to define the original landmark set. q Then, communicate this set to all nodes. Global Landmark Set Peer 6 Peer 2 Peer 1 Peer 3 Peer 6 Peer 7 Peer 4 Global Landmark Set Peer 7 Peer 4 Peer 2 Peer 4 Peer 3 Peer 2 Peer 3 Peer 1 Athens University of Economics and Business Athens, 31 st of May 2010 Peer 1 33/70

Our goal o Formulate a method which combines: n n n Minimum requirements in terms of network resources Immunity to subsequent alterations of the dataset Adaptability to network changes o Top 10 Challenge: Distributed Data Mining o Application n o Hard dimensionality reduction problems o Projecting from 500 dimensions to 10 while retaining interobjects relations o Reduction of network resources consumption State of the art: n n Distributed PCA Distributed Fast. Map Athens University of Economics and Business Athens, 31 st of May 2010 34/70

Requirements and Candidates q Requirements: q There exists some kind of network organization scheme q Physical topology q Self-Organization q Each algorithm is composed of two parts q A centrally executed q A decentralized part q Ideal Candidate: Any landmark based dimensionality reduction algorithm q Landmark selection process q Aggregation of landmarks in a central location q Derivation of the projection operator q Communication of the operator to all nodes q Projection of each point independently Athens University of Economics and Business Athens, 31 st of May 2010 35/70

Distributed FEDRA q Applying the landmark based paradigm in a network environment q Select landmarks at peer level q Communicate all landmarks to aggregator q O(nk) network load q Project landmarks and communicate the results q O(nk. M +Mk 2) network load q Each peer projects each point independently q Assuming a fixed number of |L| landmarks then network requirements are upper bounded for each algorithm q O(n|L|M+M|L|k) q Landmark based algorithms are less demanding than distributed PCA q Distributed PCA: O(Mn 2 + nk. M) q As long as |L| < n Athens University of Economics and Business Athens, 31 st of May 2010 36/70

Selecting the landmark points q Each peer may select: q k points from the local dataset q Select k local points (randomly or heuristically) q Transmit them to the aggregator q The aggregator receives Mk points from all peers and selects the landmark set. q Network load is O(Mkn + Mk 2) q k/M points from the local dataset q This implies that the aggregator will inform the peers about the size of the network q The landmarks selection happens only once in the lifetime of the network, arrivals and departures will have no affect. q Network load is O(kn + Mk 2) q Zero points from the local set q The aggregator selects from the local dataset k landmarks q Network load is O(Mk 2) Athens University of Economics and Business Athens, 31 st of May 2010 37/70

Application q. Datasets from the Pascal Large Scale Challenge 2008 q 500 -node network with random connections between elements q. Nodes are connected with 5% probability q. Distributed K-Means (P 2 P-Kmeans 1) approach in order to assess the quality of the produced embedding Dataset Cardinality n Classes k Description Alpha 500000 500 2 10: 50 Pascal Large Scale Challenge ‘ 08 Beta 500000 500 2 10: 50 Pascal Large Scale Challenge ‘ 08 Gamma 500000 500 2 10: 50 Pascal Large Scale Challenge ‘ 08 Delta 500000 500 2 10: 50 Pascal Large Scale Challenge ‘ 08 1. S. Datta, C. Giannella, H. Kargupta: Approximate Distributed K-means clustering over a P 2 P network. IEEE TKDE 2009, vol 21, no 10, 10/2009 Athens University of Economics and Business Athens, 31 st of May 2010 38/70
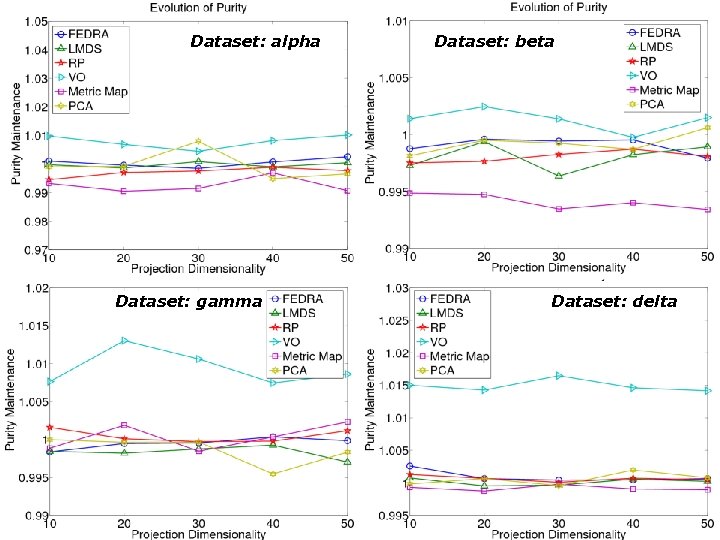
Dataset: alpha Dataset: gamma Dataset: beta Dataset: delta 39 /81
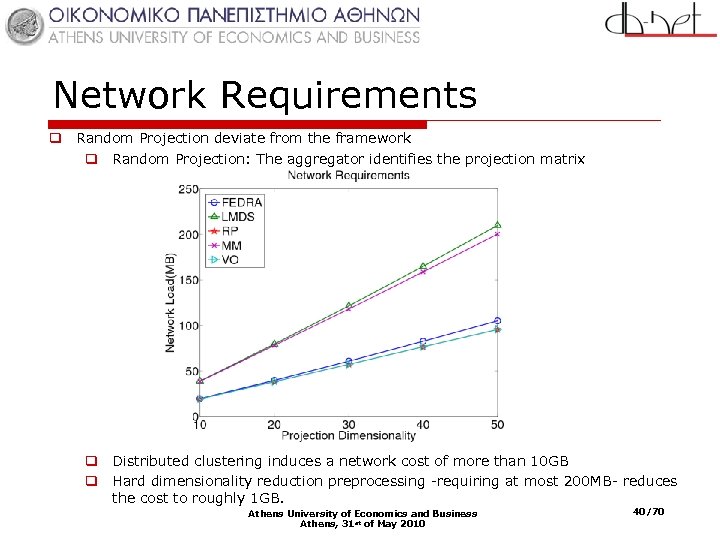
Network Requirements q Random Projection deviate from the framework q Random Projection: The aggregator identifies the projection matrix q Distributed clustering induces a network cost of more than 10 GB q Hard dimensionality reduction preprocessing -requiring at most 200 MB- reduces the cost to roughly 1 GB. Athens University of Economics and Business Athens, 31 st of May 2010 40/70

Summary q. Landmark based dimensionality reduction algorithms provide a viable solution to distributed dimensionality reduction pre-processing q. High quality results q. Low network requirements q. No special requirements in terms of network organization q. Adaptability to potential failures q. Results obtained in a network of 500 peers q. Dimensionality reduction preprocessing and subsequent P 2 P-Kmeans application necessitates only 12% of the original P 2 P-Kmeans load q. Clustering quality remains the same and slightly ameliorated q. Distributed FEDRA q. Low network requirements combined with high quality results Athens University of Economics and Business Athens, 31 st of May 2010 41/70

Distributed Non Linear Dimensionality Reduction Based on : • P. Magdalinos, M. Vazirgiannis, D. Valsamou, "Distributed Knowledge Discovery with Non Linear Dimensionality Reduction", To appear in the Proceedings of the 14 th Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD'10), Hyderabad, India, June 2010. (Acceptance Rate (full paper) 10, 2%) • P. Magdalinos, G. Tsatsaronis, M. Vazirgiannis, “Distributed Text Mining based on Non Linear Dimensionality Reduction", Submitted to European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECML-PKDD 2010), Currently under review. Athens University of Economics and Business Athens, 31 st of May 2010

Our goal o Top 10 Challenges: Distributed data mining of high dimensional data n n o Vector Space Model: n n n o Each word defines an axis each document is a vector residing in a high dimensional plane Numerous methods that try to project data in a low dimensional space while assuming linear dependence between variables. However latest experimental results show that this assumption is incorrect Application n o Scaling Up for High Dimensional Data Distributed Data Mining Hard dimensionality reduction and visualization problems o Unfolding a manifold distributed across a network of peers o Mining information from distributed text collections State of the art: n None! Athens University of Economics and Business Athens, 31 st of May 2010 43/70
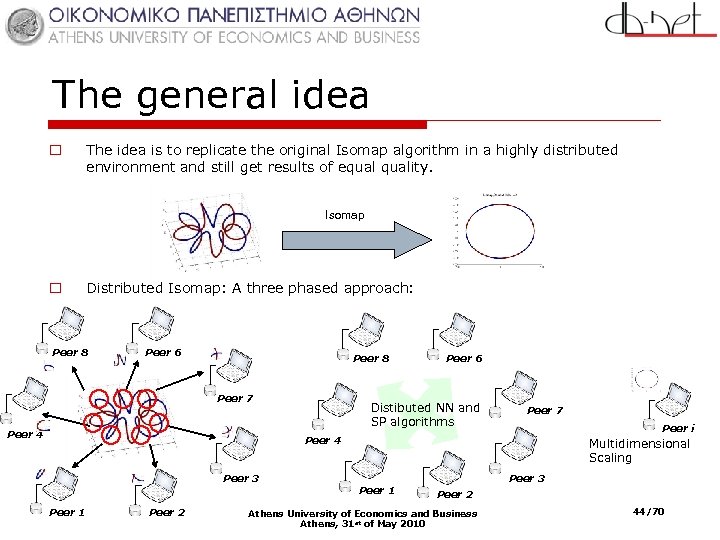
The general idea o The idea is to replicate the original Isomap algorithm in a highly distributed environment and still get results of equality. Isomap o Distributed Isomap: A three phased approach: Peer 8 Peer 6 Peer 8 Peer 7 Peer 4 Peer 6 Distibuted NN and SP algorithms Peer 7 Peer i Peer 4 Peer 3 Peer 1 Peer 2 Multidimensional Scaling Peer 1 Peer 3 Peer 2 Athens University of Economics and Business Athens, 31 st of May 2010 44/70
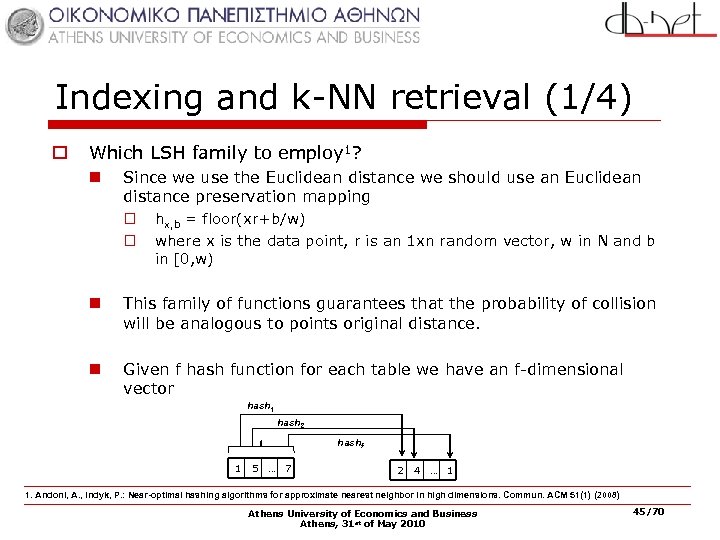
Indexing and k-NN retrieval (1/4) o Which LSH family to employ 1? n Since we use the Euclidean distance we should use an Euclidean distance preservation mapping o hx, b = floor(xr+b/w) o where x is the data point, r is an 1 xn random vector, w in N and b in [0, w) n This family of functions guarantees that the probability of collision will be analogous to points original distance. n Given f hash function for each table we have an f-dimensional vector hash 1 hash 2 hashf 1 5 … 7 2 4 … 1 1. Andoni, A. , Indyk, P. : Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions. Commun. ACM 51(1) (2008) Athens University of Economics and Business Athens, 31 st of May 2010 45/70
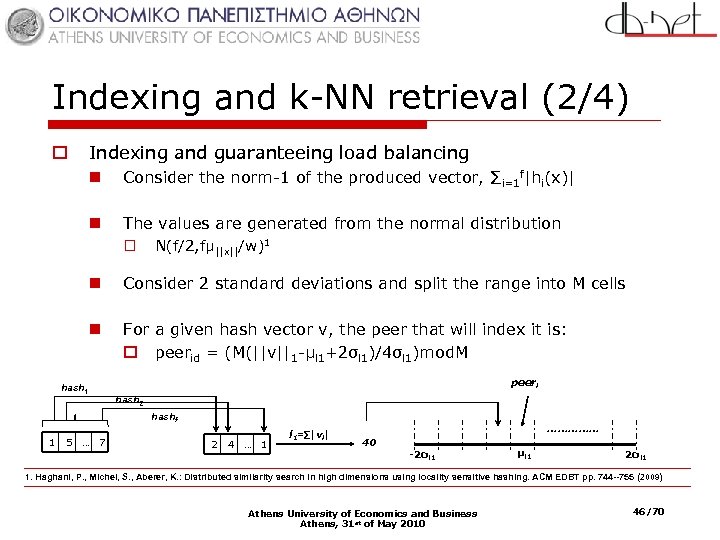
Indexing and k-NN retrieval (2/4) Indexing and guaranteeing load balancing o n Consider the norm-1 of the produced vector, ∑i=1 f|hi(x)| n The values are generated from the normal distribution o N(f/2, fμ||x||/w)1 n Consider 2 standard deviations and split the range into M cells n For a given hash vector v, the peer that will index it is: o peerid = (M(||v||1 -μl 1+2σl 1)/4σl 1)mod. M hash 1 peeri hash 2 hashf 1 5 … 7 2 4 … 1 l 1=∑|vi| …………… 40 -2σl 1 μl 1 2σl 1 1. Haghani, P. , Michel, S. , Aberer, K. : Distributed similarity search in high dimensions using locality sensitive hashing. ACM EDBT pp. 744 --755 (2009) Athens University of Economics and Business Athens, 31 st of May 2010 46/70

Indexing and k-NN retrieval (3/4) o o How to effectively and efficiently search for the k. NN of each point? Baseline: For each local point di n For each table T o Find the peer that indexes it o Retrieve all points from corresponding bucket n Retrieve actual points n Calculate actual distances, rank them and retain k-NNs o What if we could somehow identify a range and upper bound the difference of δ=| ||h(x)||1 - ||h(y)||1 |? o Theorem 5: Given f hash functions hi = floor(rix. T+bi/w) where ri is an 1 xn random vector, w∈N, bi∈[0, w), i = 1. . . f , the difference δ of the l 1 norms of the projections xf , yf of two points x, y∈Rn is upper bounded by (||A|| ||x-y||)/w, where A= || ∑i=1 f|ri| || and ||x − y|| the points’ Euclidean distance. n Although the bound is rather large, it still reduces the required number of messages Athens University of Economics and Business Athens, 31 st of May 2010 47/70
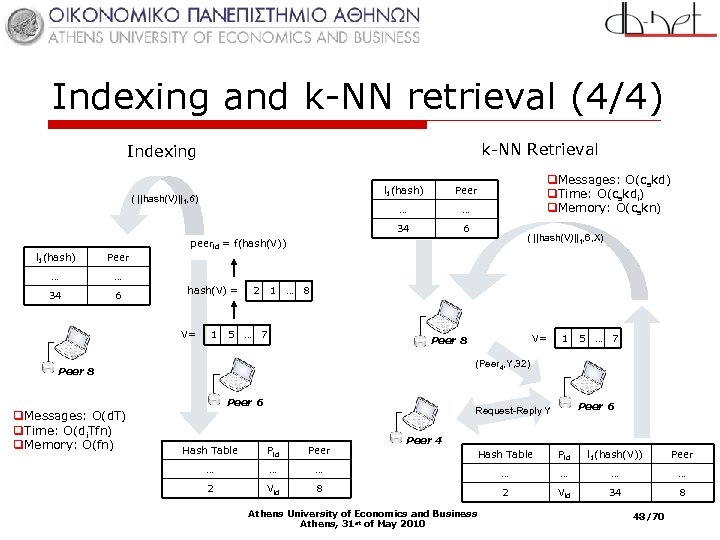
Indexing and k-NN retrieval (4/4) k-NN Retrieval Indexing l 1(hash) … … 34 ( ||hash(V)||1, 6) q. Messages: O(cskd) q. Time: O(cskdi) q. Memory: O(cskn) Peer 6 ( ||hash(V)||1, 6, X) peerid = f(hash(V)) l 1(hash) Peer … … 34 6 hash(V) = 2 1 … 7 V= 5 1 … 8 1 5 … 7 (Peer 4, Y, 32) Peer 8 Peer 6 q. Messages: O(d. T) q. Time: O(di. Tfn) q. Memory: O(fn) V= Peer 8 Peer 6 Request-Reply Y Hash Table Pid Peer … … 2 Vid Peer 4 Hash Table Pid l 1(hash(V)) Peer … … … 8 2 Vid 34 8 Athens University of Economics and Business Athens, 31 st of May 2010 48/70

Geodesic Distances (1/2) o At this step, each peer has identified the NN graphs of its points G (G=Ui=1|Di|Gi ) V 1 V 2 … Vi … V 1 Vn V 1 Vi … Vn V 2 … … V 1 V 2 … o The target is to identify the SPs from each point to the rest of the dataset o Use best practices from computer networking n Distance Vector Routing or Distributed Bellman Ford n Assume that each point is a network node and each calculated distance a link between the corresponding points/nodes o From a node’s perspective, DVR replicates a ranged search, starting with one link and progressively augmenting it by 1 Athens University of Economics and Business Athens, 31 st of May 2010 49/70
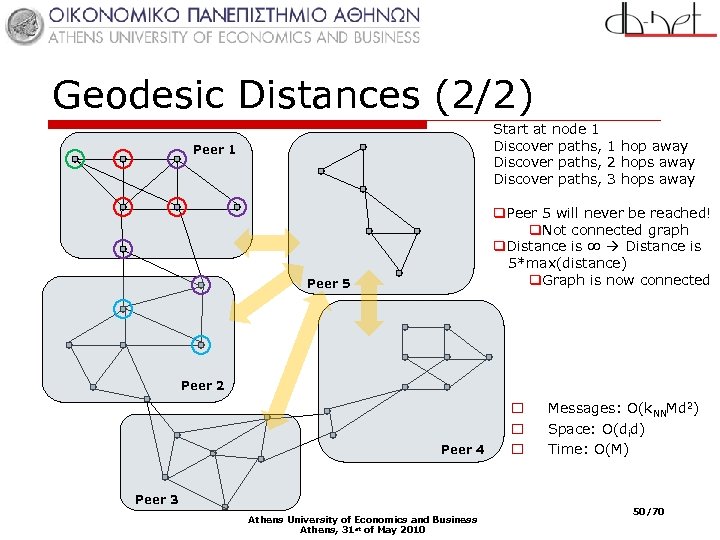
Geodesic Distances (2/2) Start at node 1 Discover paths, 1 hop away Discover paths, 2 hops away Discover paths, 3 hops away Peer 1 q. Peer 5 will never be reached! q. Not connected graph q. Distance is ∞ Distance is 5*max(distance) q. Graph is now connected Peer 5 Peer 2 Peer 4 o o o Messages: O(k. NNMd 2) Space: O(did) Time: O(M) Peer 3 Athens University of Economics and Business Athens, 31 st of May 2010 50/70
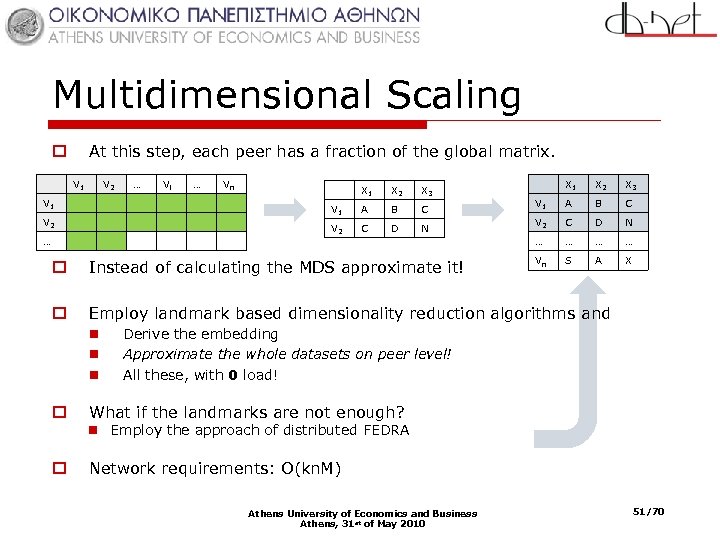
Multidimensional Scaling At this step, each peer has a fraction of the global matrix. o V 1 V 2 … Vi … Vn … X 3 A B C V 2 X 2 V 1 X 1 C D N X 1 X 2 X 3 V 1 A B C V 2 C D N … … Vn S A X o Instead of calculating the MDS approximate it! o Employ landmark based dimensionality reduction algorithms and n n n o o Derive the embedding Approximate the whole datasets on peer level! All these, with 0 load! What if the landmarks are not enough? n Employ the approach of distributed FEDRA Network requirements: O(kn. M) Athens University of Economics and Business Athens, 31 st of May 2010 51/70

Reducing Messages o Since we will work only with a small number of landmarks why not calculate their shortest paths only. o A node is randomly selected and initiates the SP process n n o Network cost n n n o Selects the required number of landmarks (i. e. a) Initiates the SP algorithm O(adk. NNM) messages Communicates results to all nodes O(Ma) messages All nodes execute the landmark based DR algorithm locally Base approach O(k. NNMd 2) Landmark based approach O(adk. NNM+Md) Landmark based approach is always cheaper. D-Isomap in total n n n Messages: O(csdk + d. T + adk. NNM) Time: O(cskdi + M) + CDLDR Space: O(cskdi + did) + CDLDR Athens University of Economics and Business Athens, 31 st of May 2010 52/70
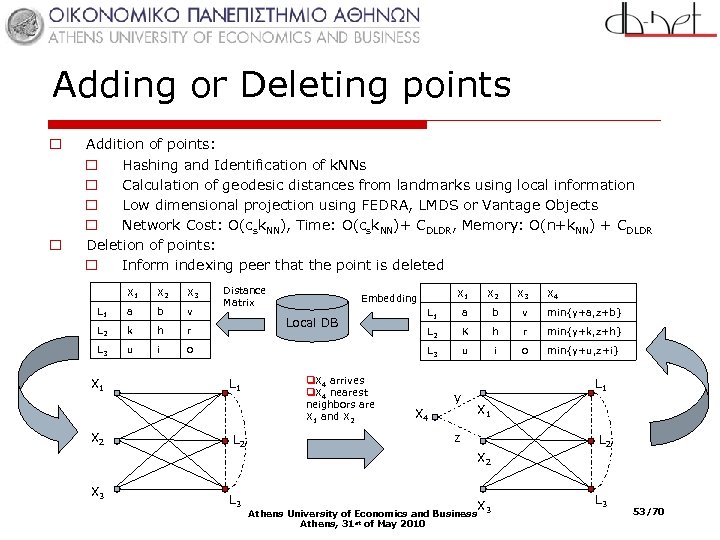
Adding or Deleting points o o Addition of points: o Hashing and Identification of k. NNs o Calculation of geodesic distances from landmarks using local information o Low dimensional projection using FEDRA, LMDS or Vantage Objects o Network Cost: O(csk. NN), Time: O(csk. NN)+ CDLDR, Memory: O(n+k. NN) + CDLDR Deletion of points: o Inform indexing peer that the point is deleted X 1 X 2 X 3 L 1 a b v L 2 k h r L 3 u i Distance Matrix o X 1 X 2 L 2 X 3 L 1 a b v min{y+a, z+b} L 2 K h r min{y+k, z+h} L 3 Local DB L 1 X 1 u i o min{y+u, z+i} Embedding q. X 4 arrives q. X 4 nearest neighbors are X 1 and X 2 y X 4 L 1 X 1 z L 2 X 3 L 3 Athens University of Economics and Business Athens, 31 st of May 2010 X 3 L 3 53/70
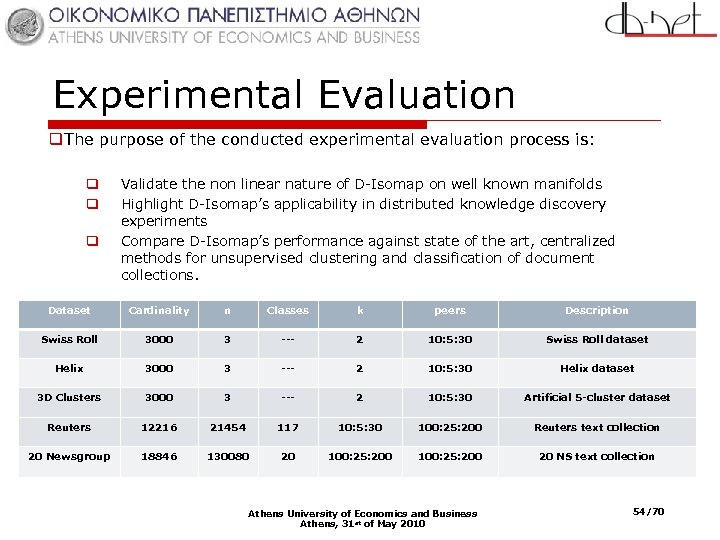
Experimental Evaluation q. The purpose of the conducted experimental evaluation process is: q q q Validate the non linear nature of D-Isomap on well known manifolds Highlight D-Isomap’s applicability in distributed knowledge discovery experiments Compare D-Isomap’s performance against state of the art, centralized methods for unsupervised clustering and classification of document collections. Dataset Cardinality n Classes k peers Description Swiss Roll 3000 3 --- 2 10: 5: 30 Swiss Roll dataset Helix 3000 3 --- 2 10: 5: 30 Helix dataset 3 D Clusters 3000 3 --- 2 10: 5: 30 Artificial 5 -cluster dataset Reuters 12216 21454 117 10: 5: 30 100: 25: 200 Reuters text collection 20 Newsgroup 18846 130080 20 100: 25: 200 20 NS text collection Athens University of Economics and Business Athens, 31 st of May 2010 54/70

Non linear manifolds (1/3) o What we expect to see: o Input: o Output: Athens University of Economics and Business Athens, 31 st of May 2010 55/70
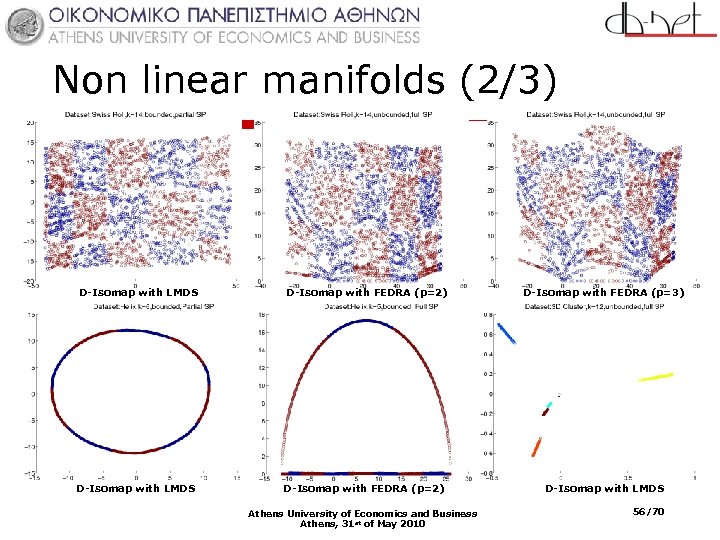
Non linear manifolds (2/3) D-Isomap with LMDS D-Isomap with FEDRA (p=2) D-Isomap with FEDRA (p=3) D-Isomap with LMDS D-Isomap with FEDRA (p=2) D-Isomap with LMDS Athens University of Economics and Business Athens, 31 st of May 2010 56/70
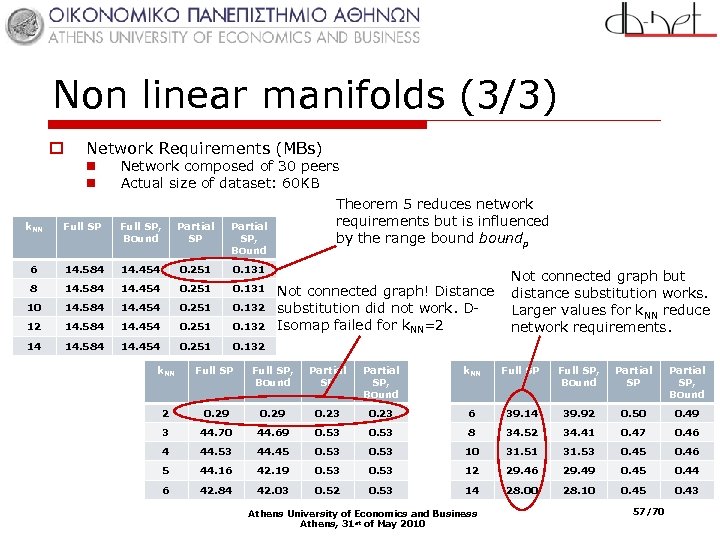
Non linear manifolds (3/3) o Network Requirements (MBs) n n Network composed of 30 peers Actual size of dataset: 60 KB k. NN Full SP, Bound Partial SP, Bound 6 14. 584 14. 454 0. 251 0. 131 8 14. 584 14. 454 0. 251 0. 131 10 14. 584 14. 454 0. 251 0. 132 12 14. 584 14. 454 0. 251 0. 132 14 14. 584 14. 454 0. 251 Theorem 5 reduces network requirements but is influenced by the range boundp 0. 132 Not connected graph! Distance substitution did not work. DIsomap failed for k. NN=2 Not connected graph but distance substitution works. Larger values for k. NN reduce network requirements. k. NN Full SP, Bound Partial SP, Bound 2 0. 29 0. 23 6 39. 14 39. 92 0. 50 0. 49 3 44. 70 44. 69 0. 53 8 34. 52 34. 41 0. 47 0. 46 4 44. 53 44. 45 0. 53 10 31. 51 31. 53 0. 45 0. 46 5 44. 16 42. 19 0. 53 12 29. 46 29. 49 0. 45 0. 44 6 42. 84 42. 03 0. 52 0. 53 14 28. 00 28. 10 0. 45 0. 43 Athens University of Economics and Business Athens, 31 st of May 2010 57/70

Text Mining with D-Isomap o We o o o compare D-Isomap with LSI LSK (kernel LSI) LPI (a hybrid of kernel LSI and Spectral Clustering) o We o o assume: 100: 25: 200 peers connected in Chord-style ring k. NN = 6: 2: 14 for LPI and D-Isomap and cs=5 for k. NN retrieval Documents are represented as vectors using Term-Frequency Norm is not normalized to 1. o Algorithms: o k-Means o k-NN (NN=7) o Metrics: o Quality maintenance defined as F-measure in Rk/ F-measure in Rn o F-measure: = 2*precision*recall/(precision+recall) o Network Load Athens University of Economics and Business Athens, 31 st of May 2010 58/70
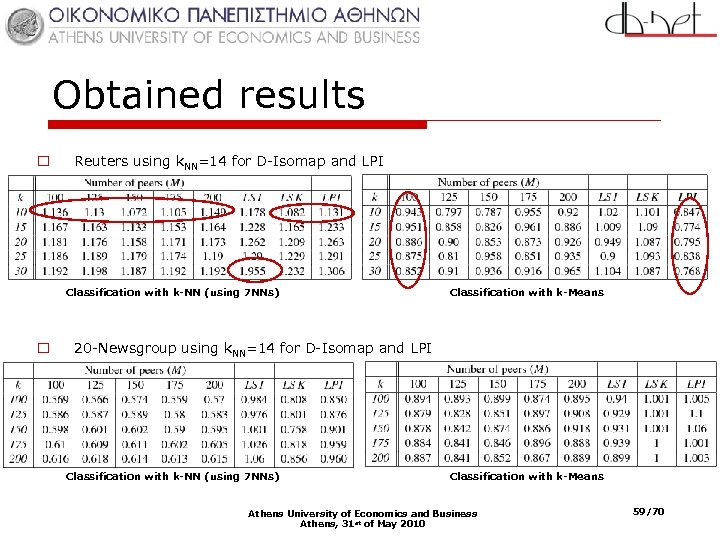
Obtained results o Reuters using k. NN=14 for D-Isomap and LPI Classification with k-NN (using 7 NNs) o Classification with k-Means 20 -Newsgroup using k. NN=14 for D-Isomap and LPI Classification with k-NN (using 7 NNs) Classification with k-Means Athens University of Economics and Business Athens, 31 st of May 2010 59/70

Network Requirements o The main disadvantage: o Network load of 4. 5 -6. 5 GB on Reuters (20 -60 MBs per node) o Network load of 3. 8 -6 GB on 20 -Newsgroup (17 -60 MBs per node) o Once in a lifetime of the network n Network load is minimized as k. NN values grow larger o Graph diameter is reduced Athens University of Economics and Business Athens, 31 st of May 2010 60/70

Summary q. Distributed Isomap: q. The first, distributed, non linear dimensionality reduction algorithm q. Manages to reveal the underlying linear nature of highly non linear manifolds q. Enhances the classification ability of k-NN q. Manages to approximately reconstruct the original dataset on a single peer node q. Results obtained in a network of 200 peers q. Experimental validation of the curse of dimensionality and the empty space phenomenon (projecting to 0. 05% of initial dimensions almost doubled the produced f-measure) q. D-Isomap managed to produce results of quality comparable and sometimes superior to central algorithms q. Disadvantage: High network requirements Athens University of Economics and Business Athens, 31 st of May 2010 61/70

x-SDR: An e. Xtensible Suite for Dimensionality Reduction Based on : • P. Magdalinos, A. Kapernekas, A. Mpiratsis, M. Vazirgiannis, “X-SDR: An Extensible Experimentation Suite for Dimensionality Reduction” Submitted to European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECML-PKDD 2010), Currently under review. • Downloadable from: • www. db-net. aueb. gr/panagis/X-SDR Athens University of Economics and Business Athens, 31 st of May 2010

The X-SDR Prototype o An open source extensible suite n n o Aggregates well known prototypes from n n o Data mining (Weka) Dimensionality reduction (MTDR suite) Key features n n n o C# and Matlab http: //www. db-net. aueb. gr/panagis/X-SDR/installation/downloads/x. SDRSC. 7 z Easily extensible by the user Does not require and special programming skills Evaluation of results through specific metrics, visualization and data mining. Exploitation n Will be used in the context of data mining and machine learning courses Athens University of Economics and Business Athens, 31 st of May 2010 63/70

Conclusions and Future Research Directions Athens University of Economics and Business Athens, 31 st of May 2010

Conclusions o. Introduced novelties o. FEDRA, a new, global, linear, approximate dimensionality reduction algorithm n Combination of low time and space requirements together with high quality results o. Definition of a methodology for the decentralization of any landmark based dimensionality reduction method n Applicable in various network topologies o. Definition of D-Isomap, the first distributed, non linear, global approximate dimensionality reduction algorithm n Application on knowledge discovery from text collections o. A prototype enabling the experimentation with dimensionality reduction methods (x-SDR) Athens University of Economics and Business Athens, 31 st of May 2010 65/70

Future Work o. D-Isomap has great potentials: o. Assume a global landmark selection process o. Given the low dimensional embedding d’ of any document d q d’ Є peeri = d’ Є peerj q hash(d’ Є peeri) = hash(d’ Є peerj) o. After termination apply a second hash function and create a new distributed hash table o o q q q Every peer is capable of answering any query. Pointers to relevant documents can be retrieved with a single message Queried peer searches locally in the approximated dataset Retrieves relevant document dr Applies the hash function and retrieves indexing peers p ind Retrieves from pind the actual host peer (ph) Cost is only a couple of bytes (hash(dr) and IP of ph) o. Focus on applying D-Isomap in a real-life scenario! Athens University of Economics and Business Athens, 31 st of May 2010 66/70

Publications Accepted: o P. Magdalinos, C. Doulkeridis, M. Vazirgiannis, “Enhancing Clustering Quality through Landmark Based Dimensionality Reduction”, Accepted with revisions in the Transactions on Knowledge Discovery from Data, Special Issue on Large Scale Data Mining – Theory and Applications. o D. Mavroeidis, P. Magdalinos, “A Sequential Sampling Framework for Spectral k. Means based on Efficient Bootstrap Accuracy Estimations: Application to Distributed Clustering”, Accepted with revisions in the Transactions on Knowledge Discovery from Data. o P. Magdalinos, M. Vazirgiannis, D. Valsamou, “Distributed Knowledge Discovery with Non Linear Dimensionality Reduction”, To appear in the Proceedings of the 14 th Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD'10), Hyderabad, India, June 2010. (Acceptance Rate (full papers) 10, 2%) o P. Magdalinos, C. Doulkeridis, M. Vazirgiannis, “FEDRA: A Fast and Efficient Dimensionality Reduction Algorithm”, In Proceedings of the SIAM International Conference on Data Mining (SDM'09), Sparks Nevada, USA, May 2009. Athens University of Economics and Business Athens, 31 st of May 2010 67/70

Publications o P. Magdalinos, C. Doulkeridis, M. Vazirgiannis “K-Landmarks: Distributed Dimensionality Reduction for Clustering Quality Maintenance”, In Proceedings of 10 th European Conference on Principles and Practice of Knowledge Discovery in Databases (PKDD'06), Berlin, Germany, September 2006. (Acceptance Rate (full papers) 8, 8%) o P. Magdalinos, C. Doulkeridis, M. Vazirgiannis, “A Novel Effective Distributed Dimensionality Reduction Algorithm”, SIAM Feature Selection for Data Mining Workshop (SIAM-FSDM‘ 06), Maryland Bethesda, April 2006. Under Review: o P. Magdalinos, G. Tsatsaronis, M. Vazirgiannis, “Distributed Text Mining based on Non Linear Dimensionality Reduction”, Submitted to European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECML-PKDD 2010), Currently under review. o P. Magdalinos, A. Kapernekas, A. Mpiratsis, M. Vazirgiannis, “X-SDR: An Extensible Experimentation Suite for Dimensionality Reduction” , Submitted to European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECML-PKDD 2010), Currently under review. Athens University of Economics and Business Athens, 31 st of May 2010 68/70

Technical Reports: o D. Mavroeidis, P. Magdalinos, M. Vazirgiannis, “Distributed PCA for Network Anomaly Detection based on Sparse PCA and Principal Subspace Stability”, AUEB 2008 Athens University of Economics and Business Athens, 31 st of May 2010 69/70

Thank you! Athens University of Economics and Business Athens, 31 st of May 2010

Back Up Slides Athens University of Economics and Business Athens, 31 st of May 2010

Intrinsic Dimensionality with… q. The Eigenvalues approach q. The number of principal components which retain variance above a certain threshold. (PCA) q. Identify a maximum eigengap which also identifies the number of data clusters (Spectral Clustering) q. The number of eigenvalues above a certain threshold q. The Stress approach q. Project the dataset (or a sample) in various target dimensionalities q. Plot the derive stress values q. Clustering and then PCA application q. Works well on non linear data q. Correlation dimensions (objects closer than r are proportional to r D) q. Compute C(r) = 2/n(n-1)Σi=1 nΣj=i+1 n. I{||xi-xj||<r} q. Plot log. C(r) versus logr Athens University of Economics and Business Athens, 31 st of May 2010 72

FEDRA requirements (ext. ) q. Artificially generated dataset: 5000 objects with 1000 dimensions q. Experimental assessment of: q. The dependence of FEDRA on the size of the dataset q. The dependence of FEDRA on the Minkowski metric (parameter c) q. Progressive augmentation of the dataset with a step of 100 objects
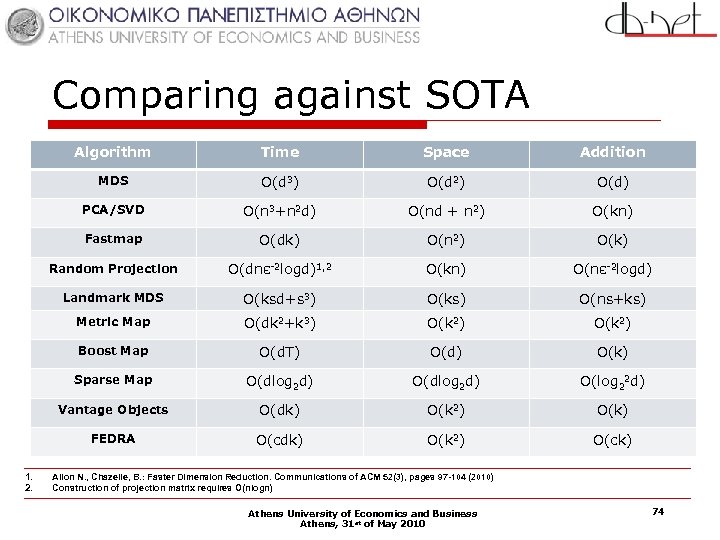
Comparing against SOTA Algorithm Space Addition MDS O(d 3) O(d 2) O(d) PCA/SVD O(n 3+n 2 d) O(nd + n 2) O(kn) Fastmap O(dk) O(n 2) O(k) Random Projection O(dnε-2 logd)1, 2 O(kn) O(nε-2 logd) Landmark MDS O(ksd+s 3) O(ks) O(ns+ks) Metric Map O(dk 2+k 3) O(k 2) Boost Map O(d. T) O(d) O(k) Sparse Map O(dlog 2 d) O(log 22 d) Vantage Objects O(dk) O(k 2) O(k) FEDRA 1. 2. Time O(cdk) O(k 2) O(ck) Ailon N. , Chazelle, B. : Faster Dimension Reduction. Communications of ACM 52(3), pages 97 -104 (2010) Construction of projection matrix requires O(nlogn) Athens University of Economics and Business Athens, 31 st of May 2010 74
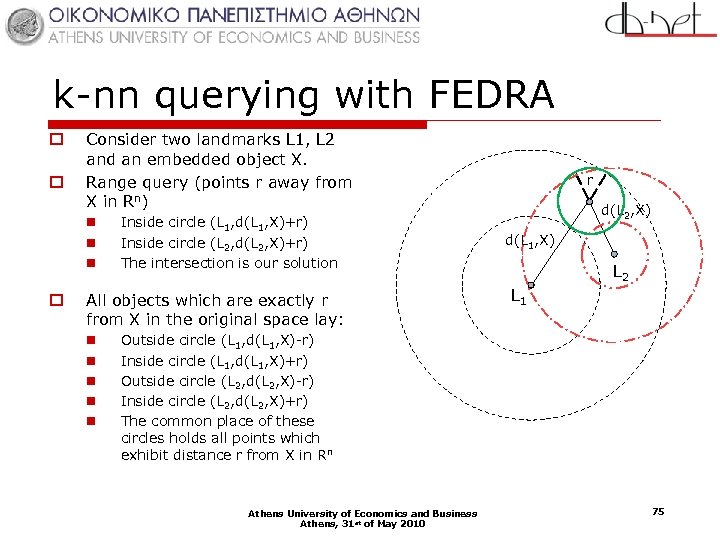
k-nn querying with FEDRA o o Consider two landmarks L 1, L 2 and an embedded object X. Range query (points r away from X in Rn) n n n o Inside circle (L 1, d(L 1, X)+r) Inside circle (L 2, d(L 2, X)+r) The intersection is our solution All objects which are exactly r from X in the original space lay: n n n r d(L 2, X) d(L 1, X) L 2 L 1 Outside circle (L 1, d(L 1, X)-r) Inside circle (L 1, d(L 1, X)+r) Outside circle (L 2, d(L 2, X)-r) Inside circle (L 2, d(L 2, X)+r) The common place of these circles holds all points which exhibit distance r from X in Rn Athens University of Economics and Business Athens, 31 st of May 2010 75
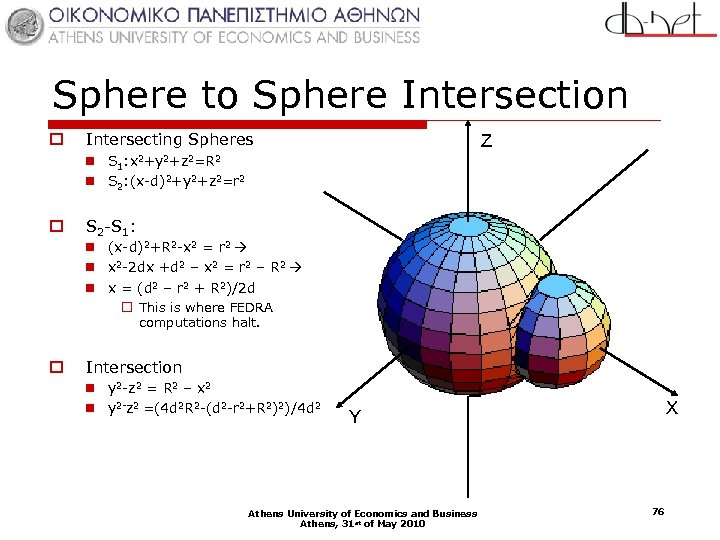
Sphere to Sphere Intersection o Intersecting Spheres Z n S 1: x 2+y 2+z 2=R 2 n S 2: (x-d)2+y 2+z 2=r 2 o S 2 -S 1: n (x-d)2+R 2 -x 2 = r 2 n x 2 -2 dx +d 2 – x 2 = r 2 – R 2 n x = (d 2 – r 2 + R 2)/2 d o This is where FEDRA computations halt. o Intersection n y 2 -z 2 = R 2 – x 2 n y 2 -z 2 =(4 d 2 R 2 -(d 2 -r 2+R 2)2)/4 d 2 X Y Athens University of Economics and Business Athens, 31 st of May 2010 76
![Random Projections (1/2) o Johnson-Lindenstrauss Lemma [1984]: n For any 0<ε<1 and any integer Random Projections (1/2) o Johnson-Lindenstrauss Lemma [1984]: n For any 0<ε<1 and any integer](https://present5.com/presentation/ed36d130ebbc4f95ac205cbfdc508805/image-77.jpg)
Random Projections (1/2) o Johnson-Lindenstrauss Lemma [1984]: n For any 0<ε<1 and any integer d let k be a positive integer such that k≥ 4(ε 2/2 -ε 3/3)-1 lnd. Then for any set V of d points in Rn there is a map of f: Rn Rk such that for all u, vЄV, (1 -ε)||u-v||2≤||f(u)-f(v)||2≤(1+ε) ||u-v||2. Further this mapping can be found in randomized polynomial time. o [Achlioptas, PODS 2001]: Two distributions n +/-1 with probability 1/2 n (√ 3)+/-1 with probability 1/6, otherwise zero o [Ailon, STOC 2006]: Cost n Theoretic: O(dkn) n Actual: Implementation dependent. Even in the most naïve implementation, it is much less, since projection matrix is 1/3 full with +/-1 o [Alon, Discrete Math 2003]: Projection matrix cannot become sparser n Only by a factor of log(1/ε) Athens University of Economics and Business Athens, 31 st of May 2010 77
![Random Projections (2/2) o Fast Johnson-Lindenstrauss Transform [Ailon, Comm ACM 2010]: n Given a Random Projections (2/2) o Fast Johnson-Lindenstrauss Transform [Ailon, Comm ACM 2010]: n Given a](https://present5.com/presentation/ed36d130ebbc4f95ac205cbfdc508805/image-78.jpg)
Random Projections (2/2) o Fast Johnson-Lindenstrauss Transform [Ailon, Comm ACM 2010]: n Given a fixed set X of d points in Rn, ε<1 and pЄ{1, 2} draw a matrix F from FJLT. With probability at least 2/3 the following two events will occur: o For any xЄX (1 -ε)ap||x||2 ≤ ||Fx||p ≤ (1+ε)ap||x||2 where a 1=k√ 2π-1 and a 2 = k o The mapping requires O(nlogn + nε-2 logd) operations o FJLT Trick: n Densification of vectors through a Fast Fourier Transform o FJLT vs Achioptas: Projection matrix is sparser than 2/3! n Advantage: Faster projection n Disadvantage: Bounds are guaranteed only for p=1, 2 o FEDRA vs Achlioptas n Achlioptas bounds are stricter than FEDRA’s n FEDRA provides bounds projecting from Lnp Lkp while Achlioptas from Ln 2 Lkp n FEDRA projects close points closer and distant points further o FEDRA vs FJLT n FJLT provides bounds for projecting from Ln 2 Lk{1, 2} Athens University of Economics and Business Athens, 31 st of May 2010 78
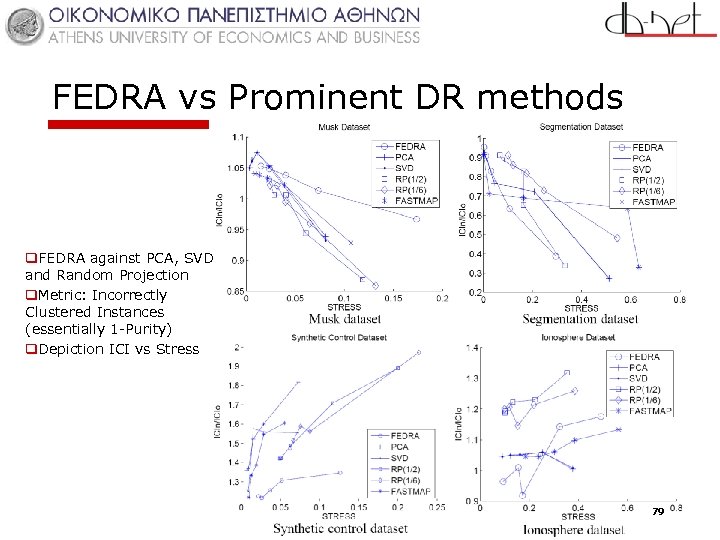
FEDRA vs Prominent DR methods q. FEDRA against PCA, SVD and Random Projection q. Metric: Incorrectly Clustered Instances (essentially 1 -Purity) q. Depiction ICI vs Stress 79
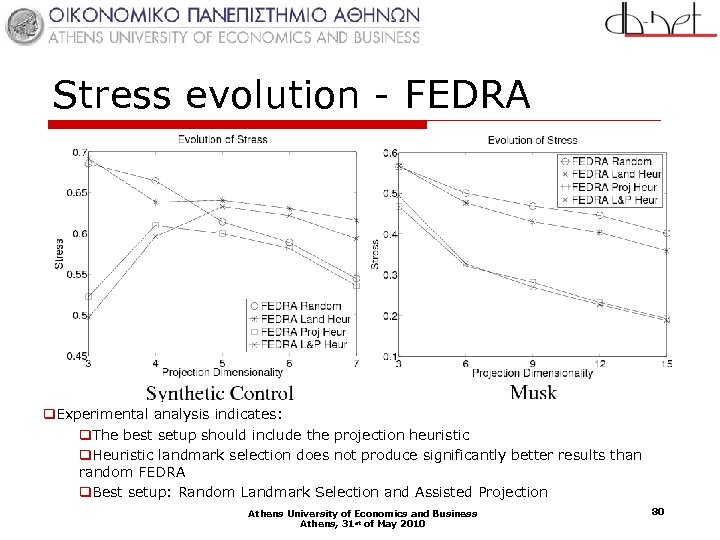
Stress evolution - FEDRA q. Experimental analysis indicates: q. The best setup should include the projection heuristic q. Heuristic landmark selection does not produce significantly better results than random FEDRA q. Best setup: Random Landmark Selection and Assisted Projection Athens University of Economics and Business Athens, 31 st of May 2010 80
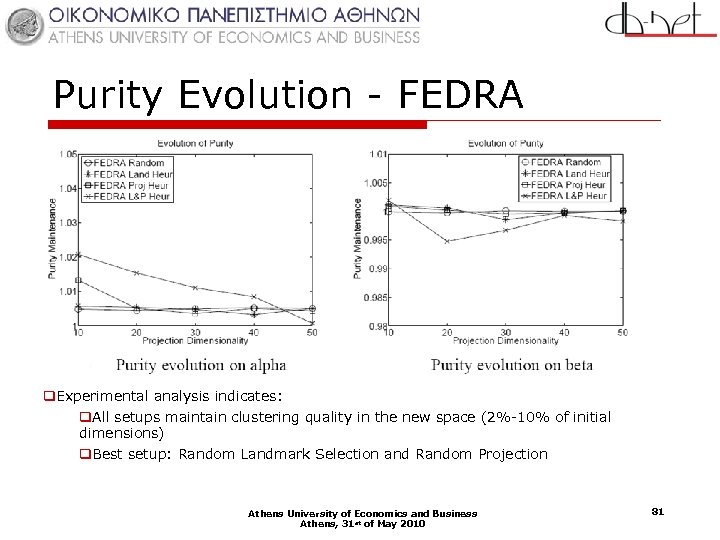
Purity Evolution - FEDRA q. Experimental analysis indicates: q. All setups maintain clustering quality in the new space (2%-10% of initial dimensions) q. Best setup: Random Landmark Selection and Random Projection Athens University of Economics and Business Athens, 31 st of May 2010 81

Time Requirements - FEDRA q. Experimental analysis indicates: q. Random FEDRA is fastest than any other configuration q. Assisted Projection is sometimes cheaper than Landmark Selection! q. Best setup: Random Landmark Selection and Random Projection Athens University of Economics and Business Athens, 31 st of May 2010 82

k-Means Convergence - FEDRA q. Experimental analysis indicates: q. All approaches exhibit approximately the same results q. Landmark Selection and Assisted Projection significantly enhance k-Means’ speed of convergence (only 10 seconds ) q. So which is the best setup? q. Based on results: Landmark Selection and Assisted Projection configuration q. Results vs Cost: Random FEDRA seems a viable compromising solution Athens University of Economics and Business Athens, 31 st of May 2010 83
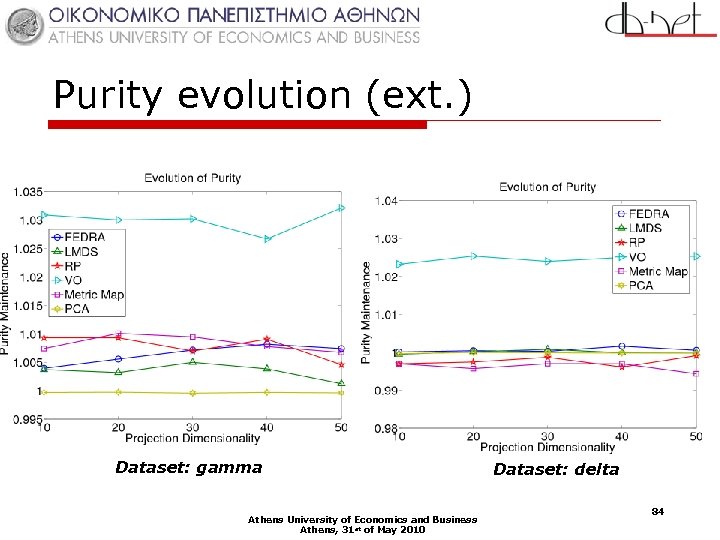
Purity evolution (ext. ) Dataset: gamma Athens University of Economics and Business Athens, 31 st of May 2010 Dataset: delta 84
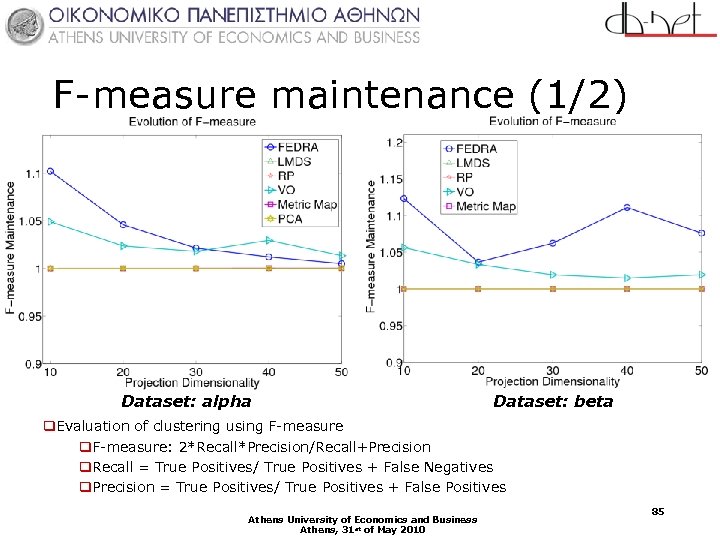
F-measure maintenance (1/2) Dataset: alpha Dataset: beta q. Evaluation of clustering using F-measure q. F-measure: 2*Recall*Precision/Recall+Precision q. Recall = True Positives/ True Positives + False Negatives q. Precision = True Positives/ True Positives + False Positives Athens University of Economics and Business Athens, 31 st of May 2010 85
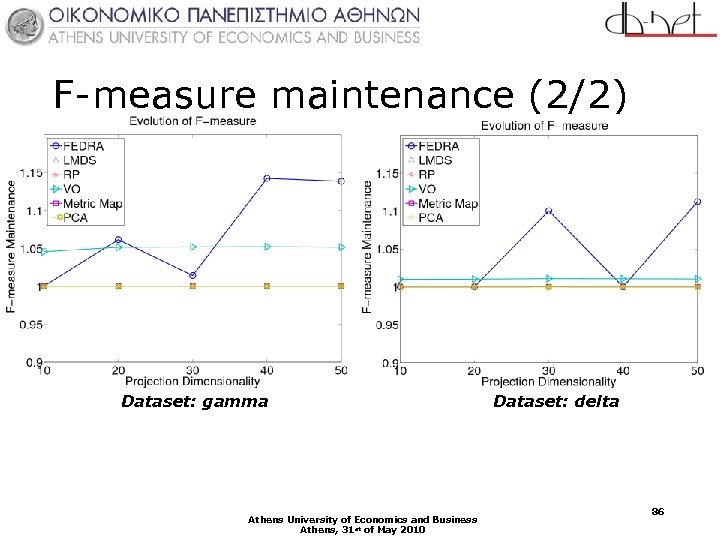
F-measure maintenance (2/2) Dataset: gamma Athens University of Economics and Business Athens, 31 st of May 2010 Dataset: delta 86
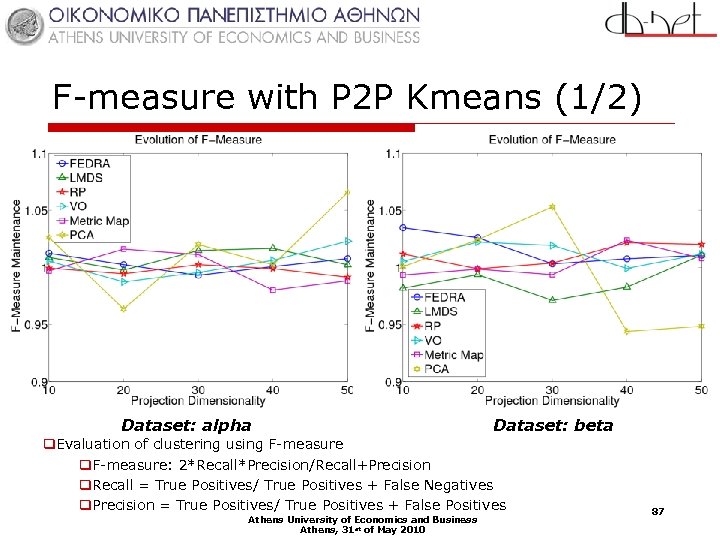
F-measure with P 2 P Kmeans (1/2) Dataset: alpha Dataset: beta q. Evaluation of clustering using F-measure q. F-measure: 2*Recall*Precision/Recall+Precision q. Recall = True Positives/ True Positives + False Negatives q. Precision = True Positives/ True Positives + False Positives Athens University of Economics and Business Athens, 31 st of May 2010 87
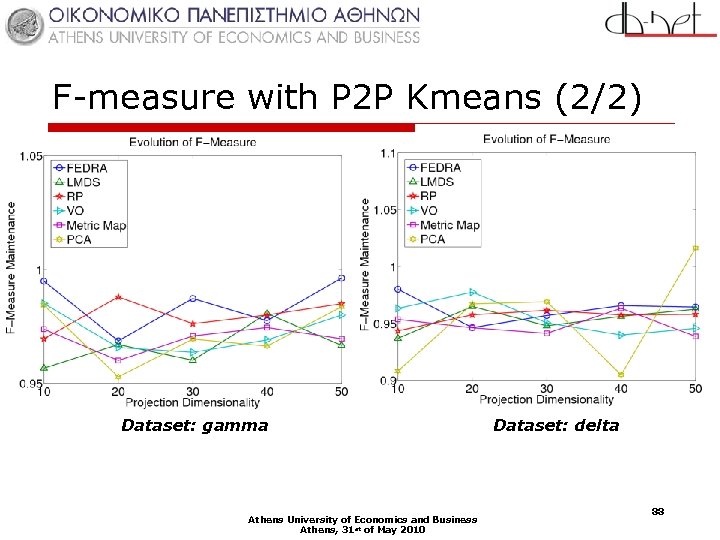
F-measure with P 2 P Kmeans (2/2) Dataset: gamma Athens University of Economics and Business Athens, 31 st of May 2010 Dataset: delta 88

D-Isomap Requirements Assumptions o We want to follow the Isomap paradigm but apply it in a network context. The following requirements rise: n Approximate NN querying results in a network context o Consider an LSH based DHT and therefore a structured P 2 P network like Chord n Calculate shortest paths in distributed environment o Consider distributed shortest path algorithms widely used routing in the internet n Approximate the multidimensional scaling o Consider landmark based dimensionality reduction approaches that operate on small fractions of the whole dataset o Assumptions: M peers organized in a Chord-ring topology. Athens University of Economics and Business Athens, 31 st of May 2010 89

p-stable distributions and LSH o Definition: n o A distribution D over R is called p-stable if there exists p≥ 0 such that for any n real numbers r 1, …, rn and i. i. d variables X 1, …, Xn with distribution D, the random variable Σiri. Xi has the same distribution as ||r||p. X where X is a random variable with distribution D. From p-stable distributions to locality sensitive hashing n n Notice that r. XT = Σiri. Xi Therefore given u 1, u 2 o dp(u 1, u 2) = ||u 1 -u 2||p o u 1 XT-u 2 XT = (u 1 -u 2)XT which is distributed as dp(u 1, u 2)XT Show if a = u 1 XT and b = u 2 XT a small value of |a-b| implies a small dp(u 1, u 2) “Small” compared to what? o Identify an interval w and map each value on this interval. n h(ui) = floor(uia. T+b/w) o Collision (i. e. same hash values) translates to small |a-b| Athens University of Economics and Business Athens, 31 st of May 2010 90

Solving non connected NG problem of Isomap o Instead of calculating the SPs calculate Minimum Spanning Trees: n k-connected sub graph n Minimal spanning tree k-edge connected n NP hard problems o Proposals: n Combination of k-edge connected MSTs [D. Zhao, L. Yang, TPAMI 2009] o Also proposes solution for updating the Shortest Path n Incremental Isomap [M. Law, K. Jain, TPAMI 2006] o Our “trick” for connected graphs n Simple and based on the intuition that if a sub-graph is separated from the rest then probably its points belong to a different cluster and therefore should be attributed a large value. o Inverse of the technique employed in [M. Vlachos et al. SIGKDD 2002] Athens University of Economics and Business Athens, 31 st of May 2010 91
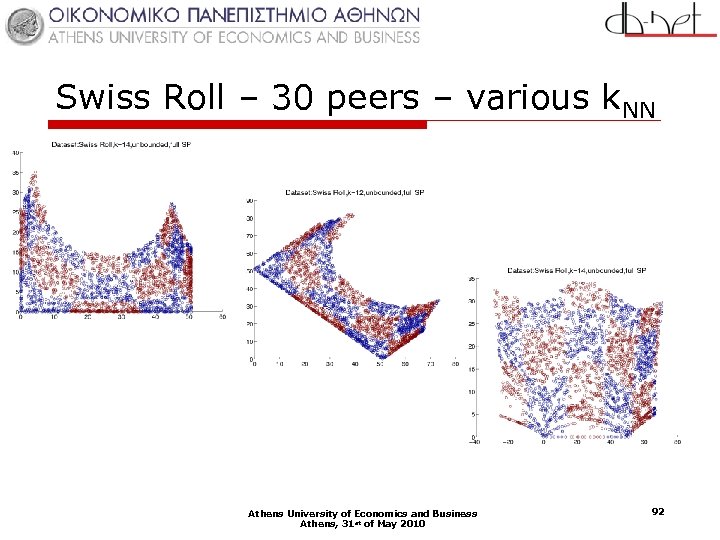
Swiss Roll – 30 peers – various k. NN Athens University of Economics and Business Athens, 31 st of May 2010 92
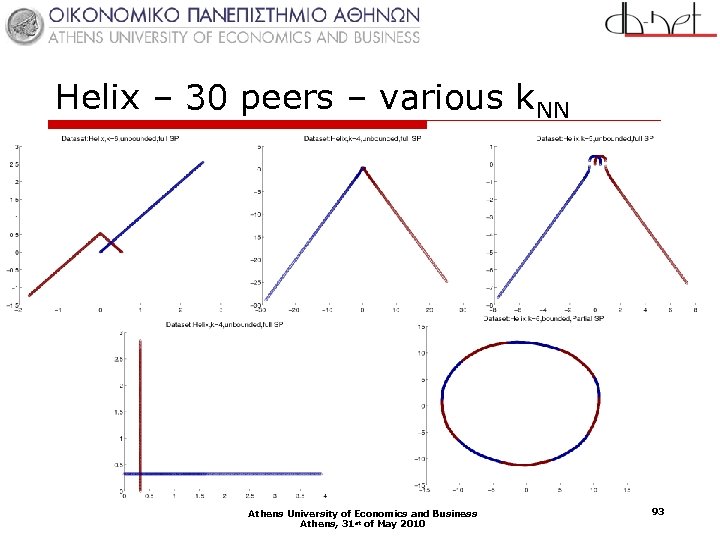
Helix – 30 peers – various k. NN Athens University of Economics and Business Athens, 31 st of May 2010 93
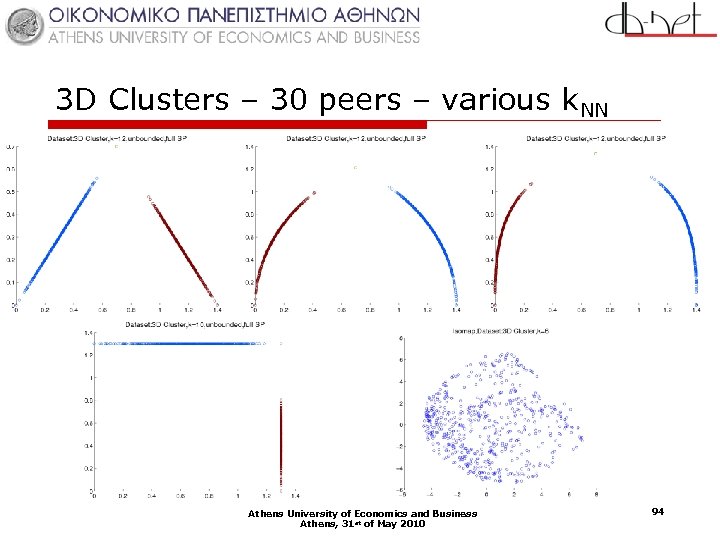
3 D Clusters – 30 peers – various k. NN Athens University of Economics and Business Athens, 31 st of May 2010 94

Original Values of k-Means and k. NN during D-Isomap experiments o k-NN classification results for NN=7 on Reuters n F-measure ~ 0. 45 (micro F-measure) o k-means clustering results for Reuters (top 10 categories) n F-measure ~ 0. 25 o k-NN classification results for NN=7 on 20 Newsgroup n F-measure ~ 0. 55 (micro F-measure) o k-means clustering results for 20 Newsgroup n F-measure ~ 0. 22 Athens University of Economics and Business Athens, 31 st of May 2010 95

Future Work (ext. ) o Extensions will concentrate on the following three axes n Minimize network requirements o Instead of requesting the actual document retrieve its projection using Random Projection (fixed ε) o Definition of a formal method (specific for each dataset) for the definition of Theorem 5 bound n Ameliorate the produced results o Apply edge-covering techniques from graph theory in order to select a good set of landmarks for the shortest path process n Enhance D-Isomap’s viability for large scale retrieval o Create clusters of nodes, all holding the same information (i. e. Crespo & Molina’s concept of SON) o Adapt techniques from routing (i. e. OSPF) so as to enable neighboring clusters to exchange information o Adapt name resolution protocol (i. e. DNS) so as to enable quick and reliable information retrieval from clusters. Athens University of Economics and Business Athens, 31 st of May 2010 96

Source Code and Results o For FEDRA and the Framework for Distributed Dimensionality Reduction: n o For D-Isomap n n o www. db-net. aueb. gr/panagis/TKDD 2009 www. db-net. aueb. gr/panagis/PAKDD 2010/ (manifold unfolding capability) www. db-net. aueb. gr/panagis/PKDD 2010/ (extensions assessment and application on text collections) For x-SDR n www. db-net. aueb. gr/panagis/X-SDR (source code, analysis, deployment instructions) Athens University of Economics and Business Athens, 31 st of May 2010 97
ed36d130ebbc4f95ac205cbfdc508805.ppt