f636eaac9937b22ecbdb6dacc5db42e7.ppt
- Количество слайдов: 46

Linear Algebra and Geometric Approches to Meaning 5 a. Concept Combination ESSLLI Summer School 2011, Ljubljana August 1 – August 7, 2011 Reinhard Blutner Universiteit van Amsterdam Reinhard Blutner 1

nhard Blutner 1 1. Outlook 2. Conditioned probabilities 3. Pitkowsky’s Correlation Polytopes 4. Conjunction and disjunction of natural concepts 5. Borderline contradictions 6. Combining prototypes 2

Vagueness • A concept is vague if it does not have precise, sharp boundaries and does not describe a well-defined set. • Vagueness is the inevitable result of a knowledge system that stores the centers rather than the boundaries of conceptual categories • Vagueness is different from typicality (centrality): - Reinhard Blutner both robins and penguins are clearly birds, but 3

Why a quantum approach? • The geometric approach provides a new theory of vagueness in the spirit of Lipman. “ It is not that people have a precise view of the world but communicate it vaguely; instead, they have a vague view of the world. I know of no model which formalizes this. I think this is the real challenge posed by the question of my title [Why is language vague? ]" [Barton L. Lipman, 2001] • It is able to solve some hard problems such as the disjunction and the conjunction puzzle • It is able to answer the question why boundary contradictions are quite acceptable (x is tall and not tall) • Extensional holism compositionality nhard Blutner coexists with intensional 4
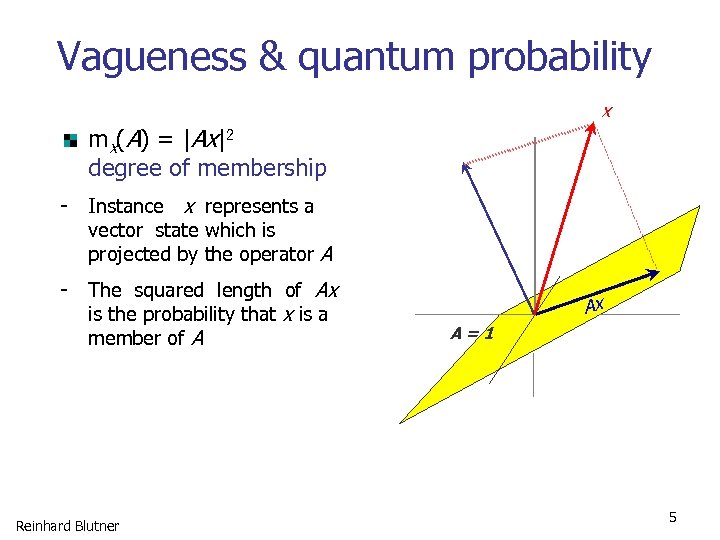
Vagueness & quantum probability x mx(A) = |Ax|2 degree of membership - Instance x represents a vector state which is projected by the operator A - The squared length of Ax is the probability that x is a member of A Reinhard Blutner Ax A=1 5

Typicality & quantum probability c x( A ) = | a x | 2 typicality - x The vector a represents the prototype of A the squared length of the projection of x onto the vector a is the probability that x collapses onto a (or a collapses onto x – symmetry) a A=1 c x( A ) m x( A ) Reinhard Blutner 6

2 1. Outlook 2. Conditioned probabilities 3. Pitkowsky’s Correlation Polytopes 4. Conjunction and disjunction of natural concepts 5. Borderline contradictions 6. Combining prototypes Reinhard Blutner 7

Conditioned Probabilities • P(A|C) = P(CA)/P(A) • (A|C) = (CAC)/ (A) (Gerd Niestegge) • If the operators commute, Niestegge’s definition reduces to classical probabilities: CAC = CCA = CA • Niestegge’s formalism is an adequate way for representing the close connection between interference effects and question order effects (non-commutativity) • Introduce ‘sequence’ (C; A) =def CAC Reinhard Blutner 8

Interference Effects • Classical: P(A) = P(A|C) P(C) + P(A| C) P( C) • Quantum: (A) = (A|C) (C) + (A|C ) (C ) + (C, A) where (C, A) = (CAC + C AC) [Interference Term] Proof Since C+C = 1, C C = CC = 0, we get Reinhard Blutner 9

Calculating the interference term • In the simplest case (when the propositions C and A correspond to projections of pure states) the interference term is easy to calculate: (C, A) = (CAC + C AC) = 2 ½ (C; A) ½ (C ; A) cos • The interference term introduces one free parameter: The phase shift . Reinhard Blutner 10

Solving the Tversky/Shafir puzzle • Tversky and Shafir (1992) show that significantly more students report they would purchase a nonrefundable Hawaiian vacation if they were to know that they have passed or failed an important exam than report they would purchase if they were not to know the outcome of the exam • (A|C) (A|C ) (A) = 0. 54 = 0. 57 = 0. 32 • (C, A) = [ (A|C) (C) + (A|C ) (C )] (A) = 0. 23 cos = -0. 43; = 2. 01 231 Reinhard Blutner 11

Conjunction Puzzle for probabilities Linda is 31 years old, single, outspoken and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations. - Linda is active in the feminist movement. (A) (6, 1) - Linda is a bank teller. (C) (3, 8) - Linda is a bank teller and is active in the feminist movement. (C&A) (5, 1) Reinhard Blutner 12

Conjunction effect • (A) = 0. 38 (Linda is a bank teller) (C) = 0. 61 (Linda is a feminist) (C ; A) = 0. 51 (Linda is a feminist bank teller) • Quantum: (C ; A) (A) = ( (C ; A) + (C, A)) Given example: (C; A) (A) = +0. 13 (sign. ) cos = 0. 7, = 2. 35 270 Reinhard Blutner 13

Approaching vagueness • Graded membership: To what degree is x a member of A ? answer: x(A) = | Ax |2 x A=1 Ax - Instances x represent vector states which are projected by the operator A - The squared length of Ax is the probability that x is a member of A • Conjunctions are represented by sequences: (C ; A) =def CAC • Disjunctions are represented by the Reinhard Blutner 14

3 1. Outlook 2. Conditioned probabilities 3. Pitkowsky’s Correlation Polytopes 4. Conjunction and disjunction of natural concepts 5. Borderline contradictions 6. Combining prototypes Reinhard Blutner 15

Kolmogorov Probabilities Monotonicity X X Y P(X) ≤ P(Y) X Y Additivity P(X)+P(Y) = P(X Y)+P(X Y) Reinhard Blutner Y X X Y Y 16
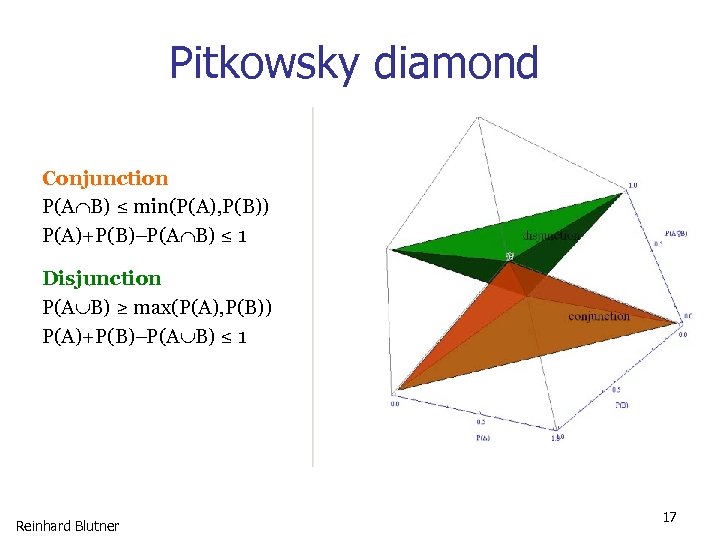
Pitkowsky diamond Conjunction P(A B) ≤ min(P(A), P(B)) P(A)+P(B) P(A B) ≤ 1 Disjunction P(A B) ≥ max(P(A), P(B)) P(A)+P(B) P(A B) ≤ 1 Reinhard Blutner 17

4 1. Outlook 2. Conditioned probabilities 3. Pitkowsky’s Correlation Polytopes 4. Conjunction and disjunction of natural concepts 5. Borderline contradictions 6. Combining prototypes Reinhard Blutner 18

Hampton 1988: judgement of membership A and B A or B overextension underextension, no additivity A Furniture Food Weapon Building Machine Bird Reinhard Blutner B Household appliances Plant Tool Dwelling Vehicle Pet A Home furnishing Hobbies Spices Instruments Pets Sportswear Fruits Household appliances B Furniture Games Herbs Tools Farmyard animals Sports equipment Vegetables Kitchen utensils 19
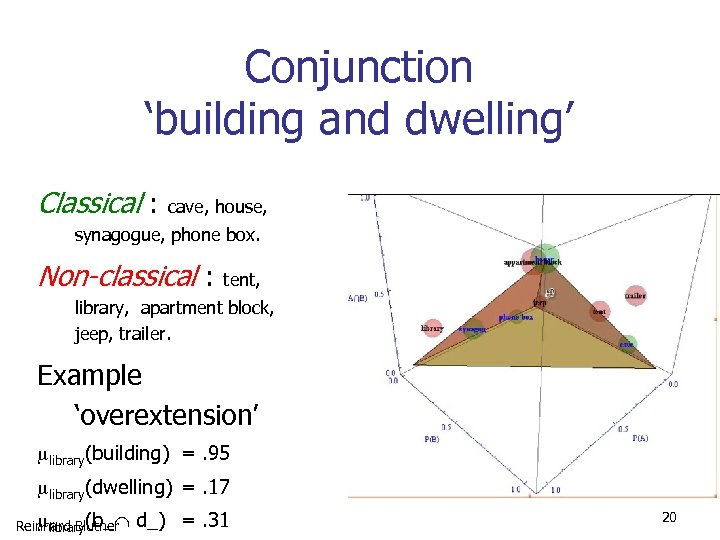
Conjunction ‘building and dwelling’ Classical : cave, house, synagogue, phone box. Non-classical : tent, library, apartment block, jeep, trailer. Example ‘overextension’ library(building) =. 95 library(dwelling) =. 17 library(b_ Reinhard Blutner d_) =. 31 20

Disjunction ‘fruits or vegetables’ Classical: pepper, pumpkin. green pepper, chili peanut, Non-classical: tomato, olive, rice, root ginger, mushroom, broccoli. Example ‘additivity’ olive(fruit) =. 5 olive(vegetable) =. 1 olive(f_ v_) =. 8 cf. Aerts 2009 Reinhard Blutner 21

5 1. Outlook 2. Conditioned probabilities 3. Pitkowsky’s Correlation Polytopes 4. Conjunction and disjunction of natural concepts 5. Borderline contradictions 6. Combining prototypes Reinhard Blutner 22

Alxatib & Pelletier 2011 Pictures with 5 persons of different size are presented. (Order of persons randomized) Subjects have to judge forms with four sentences as True/False/Can’t Tell. (Order of questions randomized) #3 #3 is is tall not tall and not tall neither tall nor not tall Reinhard Blutner True ❏ ❏ False ❏ ❏ Can’t Tell ❏ ❏ 23
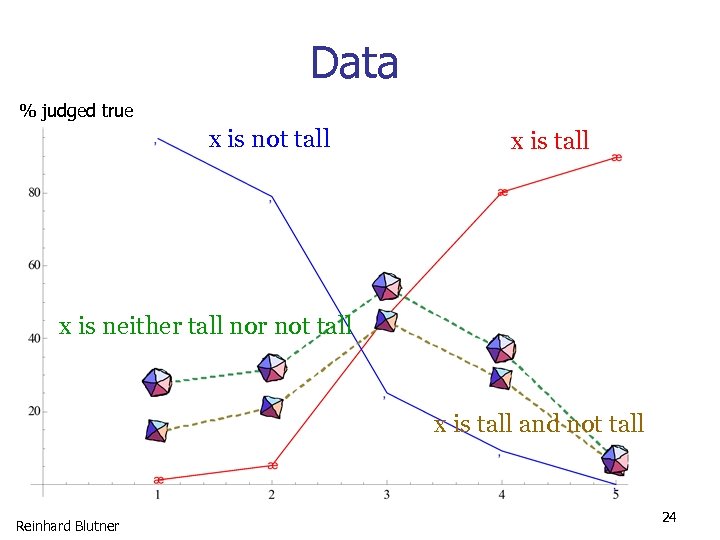
Data % judged true x is not tall x is neither tall nor not tall x is tall and not tall Reinhard Blutner 24

Tensor product as conjunction A and B : A B x x(A B) = x(A) x(B) % judged true x is tall and not tall theoretical prediction (1 parameter fitted) Reinhard Blutner 25

Extension of the formalism • So far, we have two notions for the conjunction – Asymmetric conjunction (A; B) = ABA – Tensor product A B • x( A ; A ) = 0 ; (1 - x(A)) x x ( A A ) = x ( A ) • Aerts (2009) proposes to combine both methods using the Fock space. (allowing states such as (x + x x)) • In the Fock-space, then ‘A and B ’ Reinhard Blutner 26

Two arguments • Aerts 2009: The combination is required for fitting the Hampton data of category membership • Sauerland 2010: Borderline contradictions are not extensional in the sense of fuzzy logic, i. e. x(A) = x(B) x(A and A) x(A and B) Reinhard Blutner 27

6 1. Outlook 2. Conditioned probabilities 3. Pitkowsky’s Correlation Polytopes 4. Conjunction and disjunction of natural concepts 5. Borderline contradictions 6. Combining prototypes Reinhard Blutner 28

Effect of contrast classes • A collie is a dog, but a tall collie is not a tall dog • Red nose red flag red beans • Striped apple stone lion Reinhard Blutner 29

Conjunction Effect of Typicality • x=guppy is a poorish example of a fish, and a poorish example of a pet, but it's quite a good example of a pet fish – c x( A & B ) > c x( B ) • In case of "incompatible conjunctions" such as pet fish or striped apple the conjunction effect is greater than in "compatible conjunctions“ (red apple). – cx(A‘ & B) – cx(B‘ ) > cx(A & B) – cx(B) (if A invites B but A' does not invite B') Reinhard Blutner 30

Compositional Semantics and Global Effects • Fregean Formal Semantics is based on the Principal of Compositionality • Global effects: The meaning of one part can influence the meaning of another part. Context as a global (hidden) parameter • Frege (1884) took this as an argument against compositionality in Natural Language • Quantum Cognition can explain the global contextual effects without giving up compositionality because the different constituents can be entangled. Reinhard Blutner 31

Prototypes as superposed instances • . • |ai|2 is the probability for selecting • if the prototype is not one of the presented instances it is still recognized as such. • Modification rule + recalibrating to unit length Reinhard Blutner 32

Typicality of conjoined concepts For conjoined concepts A B perform the following steps: 1. Build the corresponding vectors and 2. Construct the tensor product 3. Perform the compression operation in order to build an entangled state 4. The typicality of instance is the quantum probability that the entangled state collapses into Reinhard Blutner 33
![The compression operator • Definition • Modification • [ ] = • The resulting The compression operator • Definition • Modification • [ ] = • The resulting](https://present5.com/presentation/f636eaac9937b22ecbdb6dacc5db42e7/image-34.jpg)
The compression operator • Definition • Modification • [ ] = • The resulting state is entangled, i. e. Reinhard Blutner 34
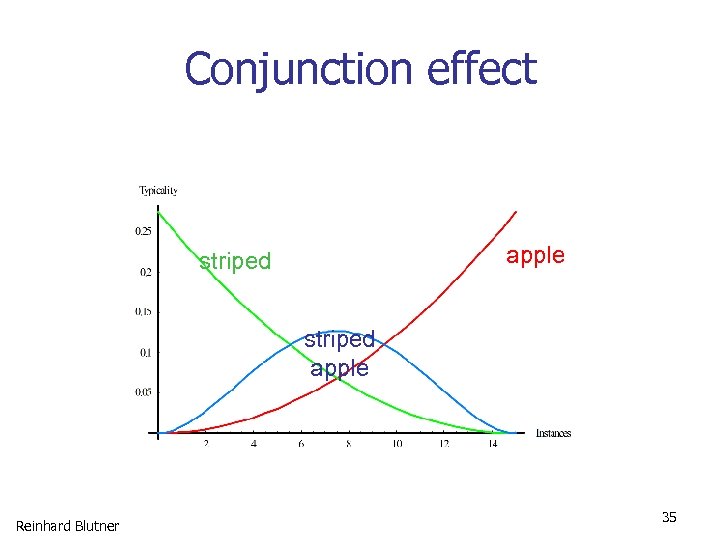
Conjunction effect apple striped apple Reinhard Blutner 35
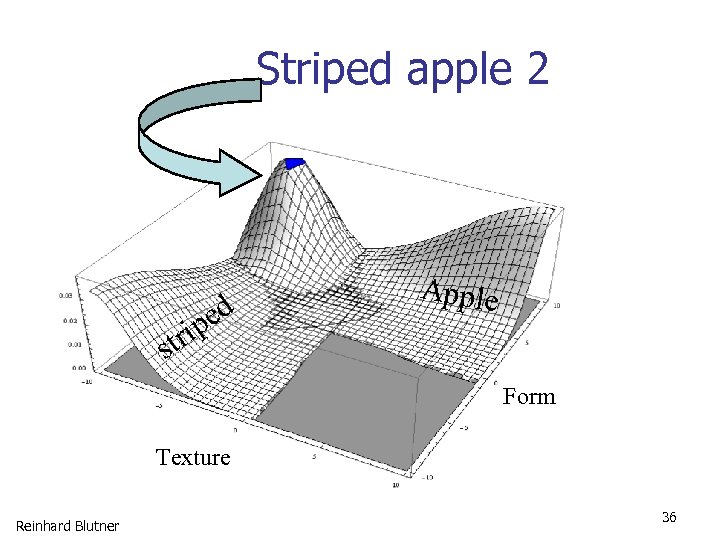
Striped apple 2 str ed ip Apple Form Texture Reinhard Blutner 36
Concept combination: a geometrical model (Peter Gärdenfors) Reinhard Blutner 37
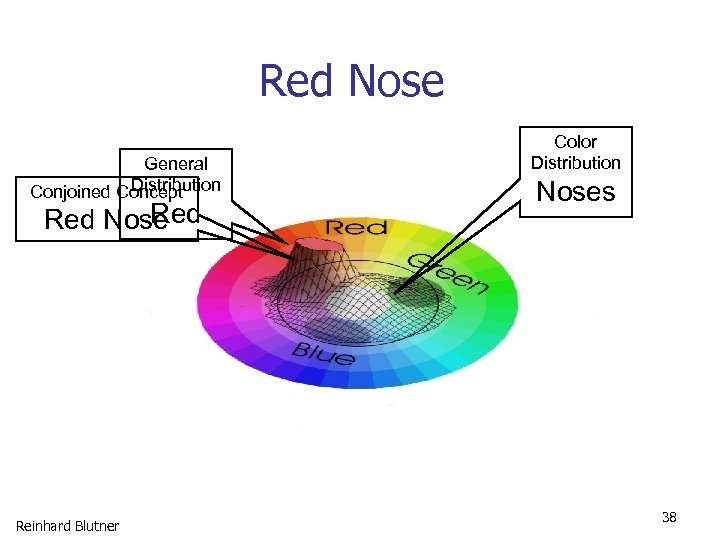
Red Nose General Distribution Conjoined Concept Red Nose Reinhard Blutner Color Distribution Noses 38
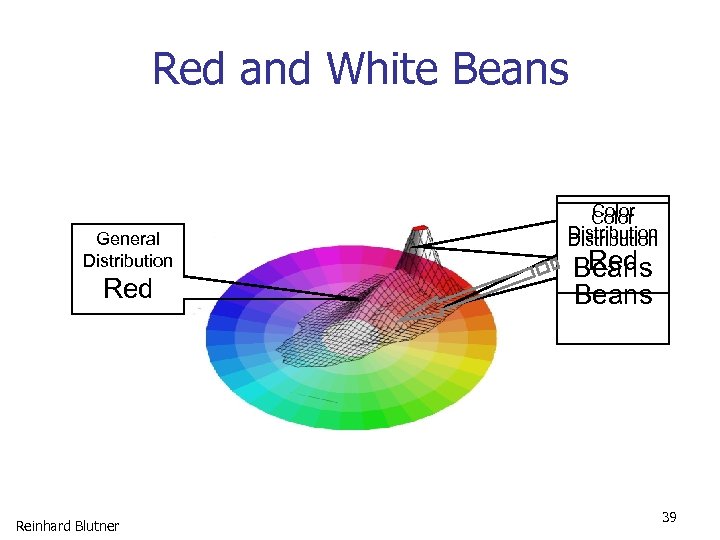
Red and White Beans General Distribution Red Reinhard Blutner Color Distribution Red Beans 39
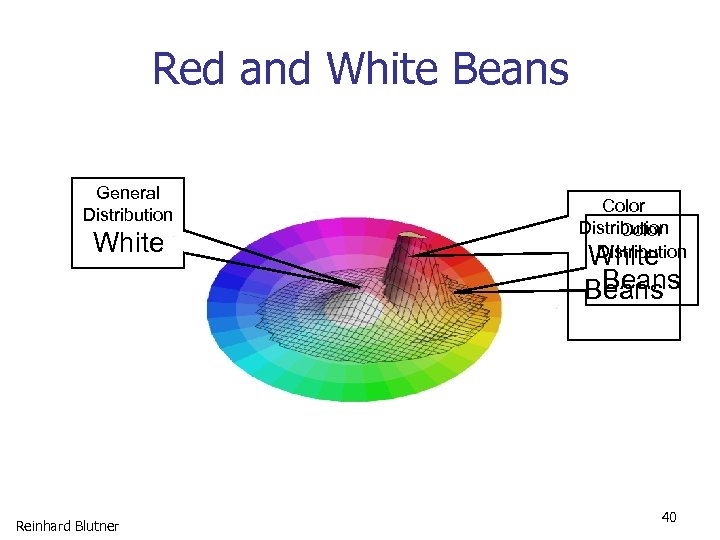
Red and White Beans General Distribution White Color Distribution White Beans Reinhard Blutner 40
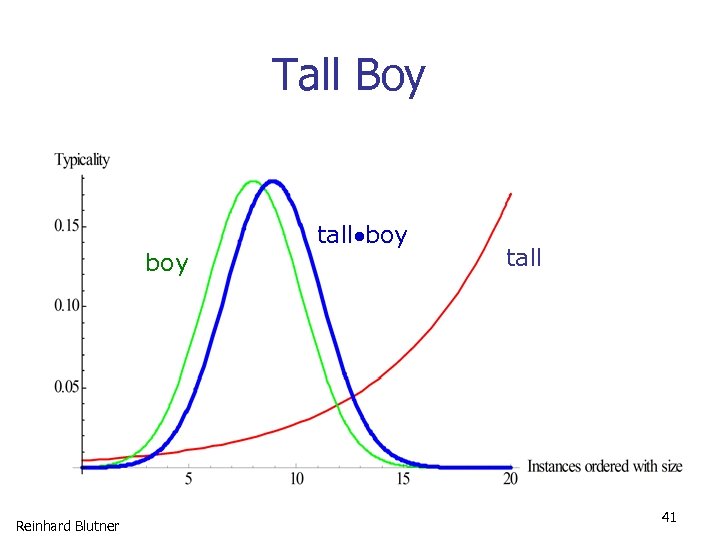
Tall Boy boy Reinhard Blutner tall boy tall 41
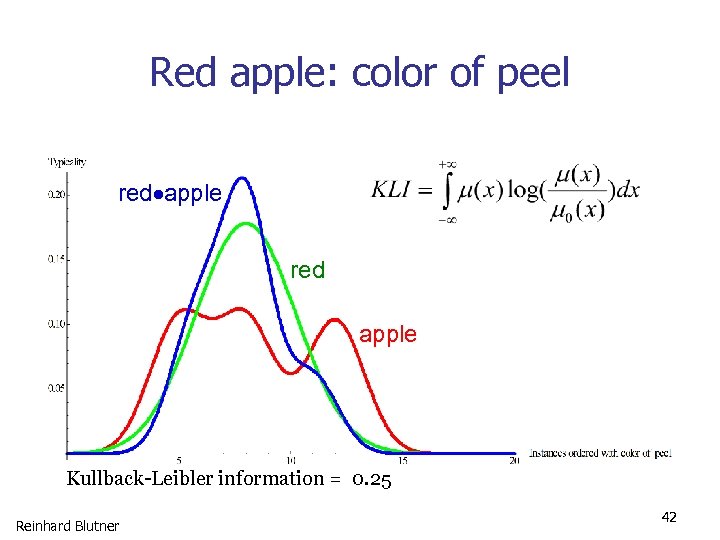
Red apple: color of peel red apple Kullback-Leibler information = 0. 25 Reinhard Blutner 42
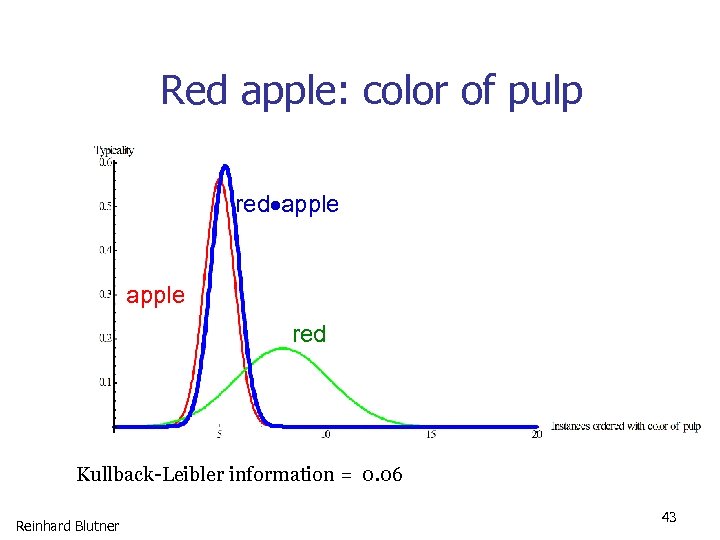
Red apple: color of pulp red apple red Kullback-Leibler information = 0. 06 Reinhard Blutner 43
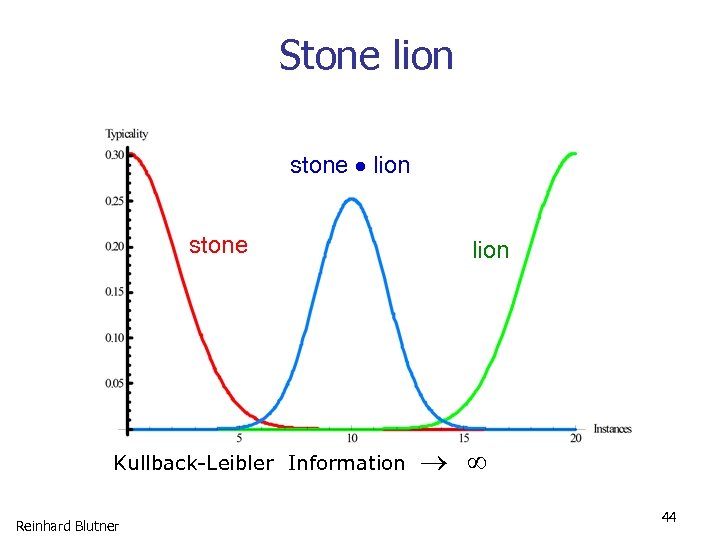
Stone lion stone Kullback-Leibler Information Reinhard Blutner lion 44

Conclusions • Several examples of context-sensitivity can be treated in a straightforward way by using a compositional operation on conceptual states. • Since conceptual states contain (frozen) usage information, they combine semantic and pragmatic information. • It makes superfluous ‘truth-conditional pragmatics’ as an inferential theory. • The present account is non-inferential; it is ‘as direct as perception’ (cf. Millikan, Recanati). Reinhard Blutner 45

General Conclusions • Asymmetric conjunction accounts for interference effects – Explaining probability judgments. If quantum probabilities are rational constructs then this kind of rationality conforms to the judgment data – Describing the combination of vague concepts – Problems with borderline contradictions can be overcome by using the Fock space. • The combination of prototypes likewise is using the Fock space and particular compression operations Reinhard Blutner 46
f636eaac9937b22ecbdb6dacc5db42e7.ppt