77e84f05c3caa774dc4e865f66959262.ppt
- Количество слайдов: 60

Lib. TW Thomas van Dijk Jan-Pieter van den Heuvel Wouter Slob

“Experimentation Project” o o Title: Computing Treewidth Supervisor: Hans Bodlaender

Goals: o o Implement algorithms to evaluate performance and quality The implementation should be a coherent library

Some statistics o Code: n n o 101 5411 Algorithms: n n o Number of classes: Lines of actual code: Number of algorithms: Lines of actual code: 30 2576 Coffee n n Amount consumed: Code per coffee: ~70 L ~77 lines / L

Using Lib. TW

Usage: getting a graph o NGraph<Input. Data> g = null; o Graph. Input input = new Dgf. Reader( “some. Graph. dgf" ); o try { g = input. get(); } catch (Input. Exception e) {}

Usage: getting a graph o NGraph<Input. Data> g = null; o Graph. Input input = new Random. Graph. Generator(10, 0. 5); o try { g = input. get(); } catch (Input. Exception e) {}

Usage: getting a graph o NGraph<Input. Data> g = null; o Graph. Input input = new Clique. Graph. Generator(7); o try { g = input. get(); } catch (Input. Exception e) {}

Usage: getting a graph o NGraph<Input. Data> g = null; o Graph. Input input = new NQueen. Graph. Generator(7); o try { g = input. get(); } catch (Input. Exception e) {}

Usage: running algorithms o Lower. Bound<Input. Data> algo = new Min. Degree<Input. Data> (); o o algo. set. Input( g ); algo. run(); o … = algo. get. Lower. Bound();

Usage: running algorithms o Lower. Bound<Input. Data> algo = new Minor. Min. Width<…>(); o o algo. set. Input( g ); algo. run(); o … = algo. get. Lower. Bound();

Usage: running algorithms o Upper. Bound<Input. Data> algo = new Greedy. Fill. In<Input. Data>(); o o algo. set. Input( g ); algo. run(); o … = algo. get. Upper. Bound();

Usage: running algorithms o Permutation<Input. Data> algo = new Quick. BB<…>(); o o algo. set. Input( g ); algo. run(); o … = algo. get. Permutation();

Usage: running algorithms o Exact<Input. Data> algo = new Treewidth. DP<Input. Data>(); o o algo. set. Input( g ); algo. run(); o … = algo. get. Treewidth();

Some practical issues

Revision control system o Essential o We used Subversion n which is very nice

Regression testing o o Automated system Currently 122 tests n o o E. g. “If you run Greedy. Degree on celar 02. dgf, the result should be 10. ” Actually stopped us from introducing bugs once or twice Good for confidence!

Visualization o o Nice to draw graphs: can visualize results and even intermediate steps of an algorithm. Complicated to implement?

Visualization o Complicated to implement? n o Not at all! Just generate ‘dot’ code and pipe it though Graph. Viz. Really easy.
![Visualization o graph G { v 1 [label="A"] v 2 [label="B"] … v 6 Visualization o graph G { v 1 [label="A"] v 2 [label="B"] … v 6](https://present5.com/presentation/77e84f05c3caa774dc4e865f66959262/image-20.jpg)
Visualization o graph G { v 1 [label="A"] v 2 [label="B"] … v 6 -- v 7 v 4 -- v 6 v 1 -- v 3 … }
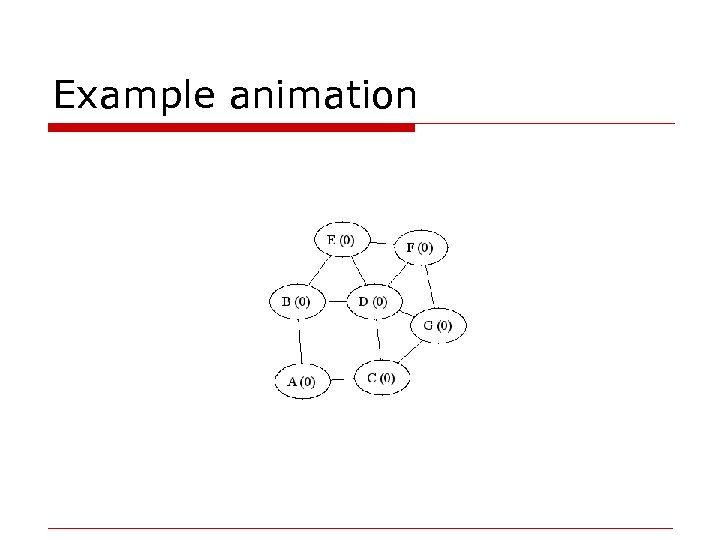
Example animation
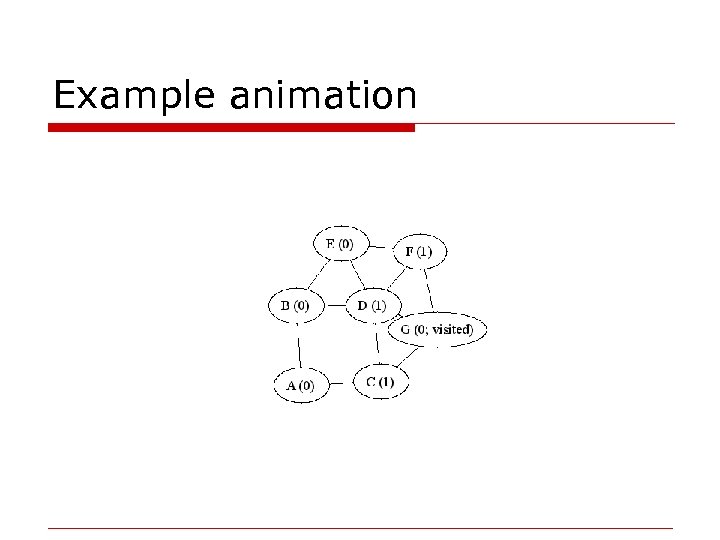
Example animation
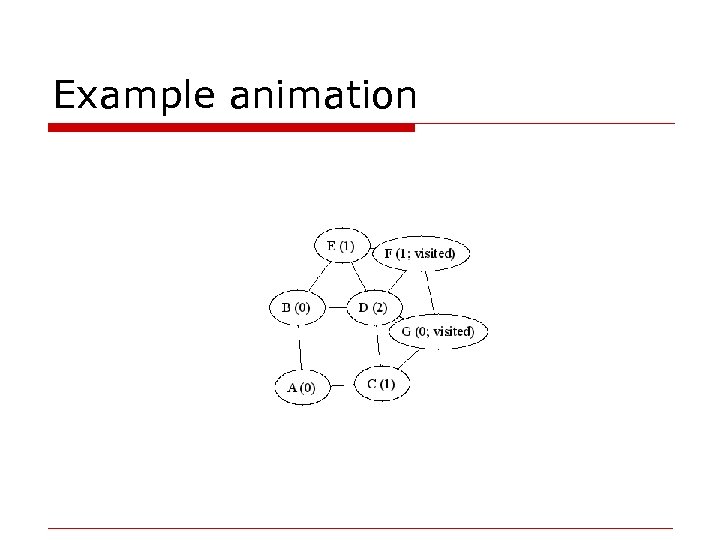
Example animation
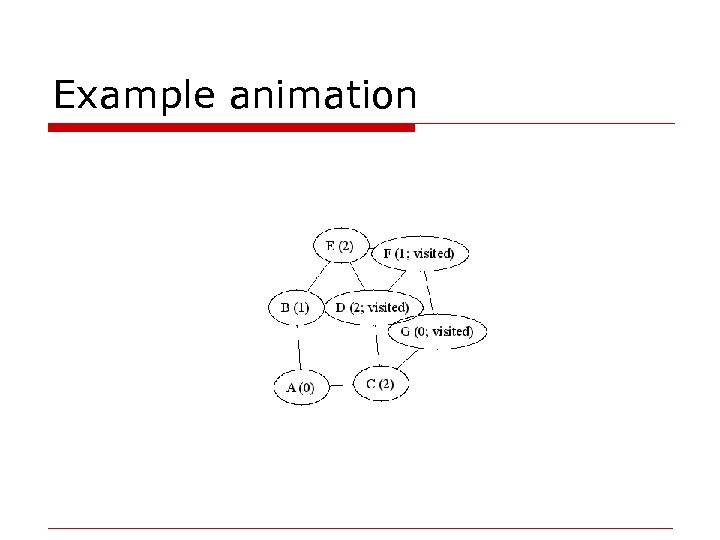
Example animation
Example animation
Example animation
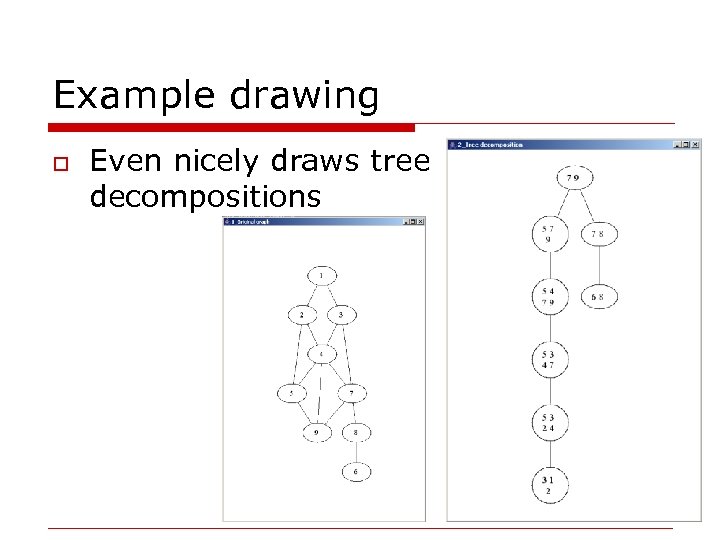
Example drawing o Even nicely draws tree decompositions

Experimental results

Lowerbounds

Lowerbounds o o All run pretty fast No effort was made to implement them very efficiently Only interested in the answer (This does hurt algorithms which calculate lowerbounds very often. More on that later. )

“All start” variants o Most lowerbound algorithms are not entirely specific n o In our implementation: n n o “Choose the vertex of minimum degree” Arbitrary choice, or Branch only on first choice: “All-start” Full branching is not worth it
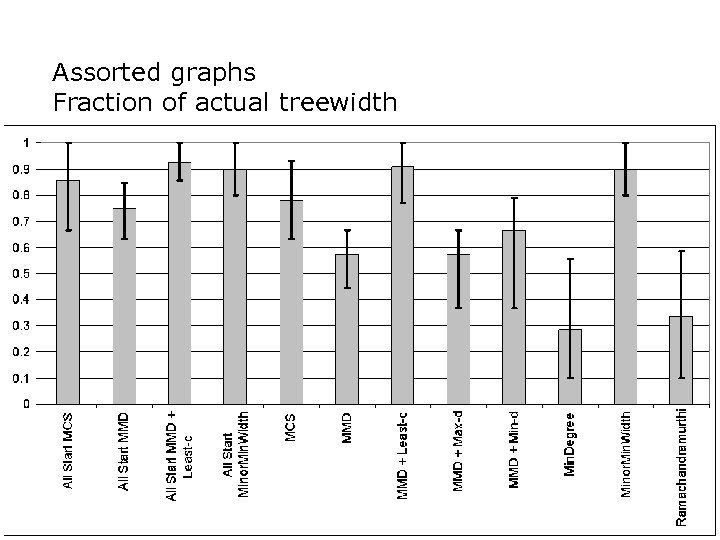
Assorted graphs Fraction of actual treewidth
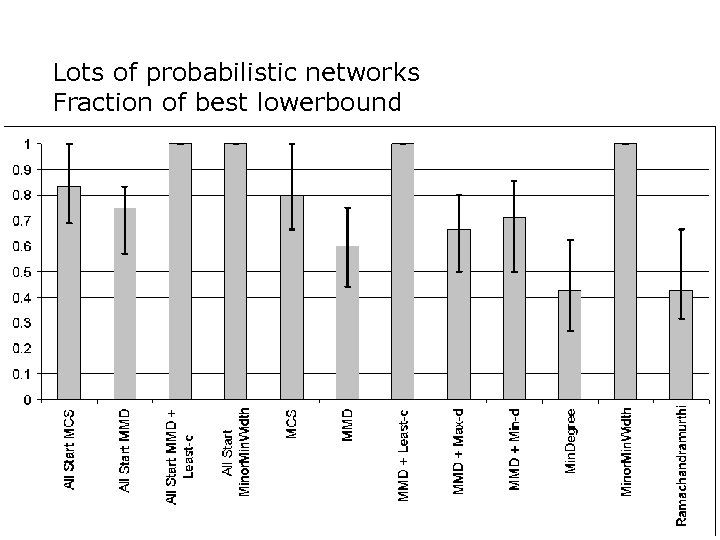
Lots of probabilistic networks Fraction of best lowerbound

Lowerbound conclusions o Two clear winners n n Maximum Minimum Degree Least-C Minor Min Width

Upperbounds

Upperbounds o As with lowerbounds: n n n all are fast only care about the answer our implementation is not for speed
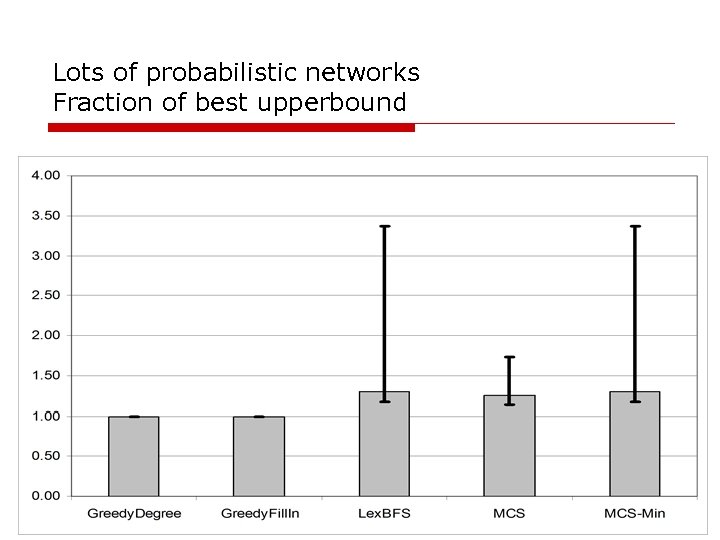
Lots of probabilistic networks Fraction of best upperbound

Upperbound conclusions o Greedy. Degree and Greedy. Fill. In are never worse than any of the others

Greedy. Degree vs Greedy. Fill. In o Experience during project n n n o Often equal Sometimes Fill. In is better Very rarely, Degree is better On 58 probabilistic networks n n n Equal: 48 times Greedy. Degree never better Fill. In is better: o o 7 times by difference one 3 times by difference four

Lowerbound = upperbound o o Seemed to happen quite often on probabilistic networks Tested on 59 probabilistic networks n n 27 had lowerbound = upperbound for some combination of algorithms Average gap of 0. 93

Quick-BB

Quick-BB o o o By Gogate & Dechter Permutations of vertices give a tree decomposition: elimination order Branch and bound n n Branch on which vertex is next in the permutation ‘Eliminate’ that vertex in that branch

Quick-BB implementation o Going into a branch involves a vertex elimination n o A different one for each branch Solution: work with ‘diffs’ n n Remember which edges were added going into a branch Remove them when coming out of the branch

Quick-BB implementation o o Use minor-min-width as lowerbound in the BB nodes MMW does edge contractions n n A typical implementation destroys the graph on the way: would require a copy Solution: second set of edge lists, destroy those during MMW, cheap to reset from old lists.

Quick-BB implementation o o o Don’t need to branch on simplical or almost simplicial vertices Checking only at the start hardly makes a difference Checking at every branch actually makes things slower n Our implementation can probably be improved

Quick-BB implementation o o Memorize branch-and-bound nodes Idea by Stan van Hoesel n o o We heard about it from Hans Bodlaender Factor 15~20 speed increase! At a memory cost, of course, but not prohibitive

Quick-BB implementation o o Start with initial permutation from an upperbound algorithm Doesn’t seem to matter much

Quick-BB evaluation o o o We don’t achieve the performance Gogate&Dechter report in their paper Gogate&Dechter’s implementation is often faster than they report in their paper But not always, and seems buggy

Treewidth DP

Treewidth DP o o Bodlaender & Fomin & Koster & Kratsch & Thilikos Existing implementation in TOL

Tw. DP implementation o o Works a lot with subsets of the vertices Implemented as Bit. Sets, not vectors

Tw. DP implementation o Need to calculate “Q-values” a lot n o o Calculated via a DFS Actually equal within a connected component Modify the DFS to take advantage of this

Tw. DP implementation o o “Bodlaender’s Clique Trick” Forall cliques in the graph: exists an optimal elimination ordering with that clique at the end Having chosen a clique, you can ignore those vertices and “dump them at the end” Bigger clique is better. . . so find maximum clique

Clique experiments o o o Funny to solve NP-hard problems as preprocessing But it really makes all the difference We do really simple backtracking to find the clique n Time dominated by the rest of the algorithm anyway

Clique experiments o “Mainuk” n n Probabilistic network with 48 vertices Max clique of 8 Without trick: 62 seconds, 33 MB With trick: 24 seconds, 17 MB

Clique experiments o “Ship-ship-pp” n n Probabilistic network with 30 vertices Max clique of 4 Without trick: 367 seconds, 271 MB With trick: 71 seconds, 77 MB

Tw. DP evaluation o Our runtime comes very close to TOL on the same machine n n n o About 1. 5 times slower Sometimes faster Similar memory usage We go way faster on the N-Queen graphs, somehow

Further work o Treewidth DP n Dealing with out-of-memory situation o o Throw tables away Fall back to B&B … Quick-BB n n Add the ‘clique trick’ here Other lowerbounds or combinations of lowerbounds

Further work o More graph implementations n n o Framework can handle this Some algorithms might benefit a lot from ‘tailor-made’ data structures Smarter checking for simplicial vertices in Quick. BB

Questions? o Slides, report and snapshot of the software on www. treewidth. com n Should be online next week
77e84f05c3caa774dc4e865f66959262.ppt