Let s Get Ready To Play Some

Let’s Get Ready To Play Some. . .

JEOPARDY

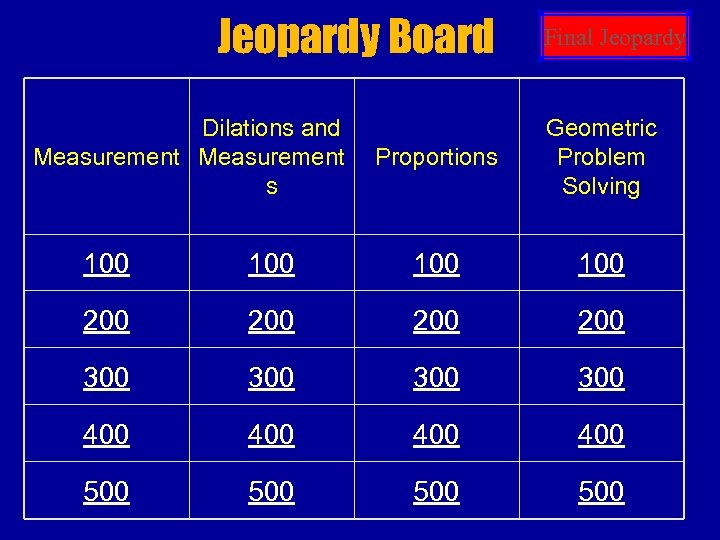Jeopardy Board Dilations and Measurement s Final Jeopardy Proportions Geometric Problem Solving 100 100 200 200 300 300 400 400 500 500

Measurement 100 The net of a cylinder is shown below. Use the ruler on the Mathematics Chart to measure the dimensions of the cylinder to the nearest inch. Which is closest to the total surface area of this cylinder? F 4 in. 2 G 11 in. 2 H 14 in. 2 J 25 in. 2 Board Answer

Measurement 100 The net of a cylinder is shown below. Use the ruler on the Mathematics Chart to measure the dimensions of the cylinder to the nearest inch. Which is closest to the total surface area of this cylinder? F 4 in. 2 G 11 in. 2 H 14 in. 2 J 25 in. 2 Board Length _______ 3 in

Measurement 100 The net of a cylinder is shown below. Use the ruler on the Mathematics Chart to measure the dimensions of the cylinder to the nearest inch. Which is closest to the total surface area of this cylinder? Area = 12 in 2 Lateral Area Only F 4 in. 2 G 11 in. 2 Width _______ 4 in H 14 in. 2 J 25 in. 2 Board Length _______ 3 in

Measurement 100 The net of a cylinder is shown below. Use the ruler on the Mathematics Chart to measure the dimensions of the cylinder to the nearest inch. Which is closest to the total surface area of this cylinder? Circles Area = 12 in 2 F 4 in. 2 Radius = ______ Lateral Area Only G 11 in. 2 As a decimal Two Circles Width _______ Total Surface 4 in 2 H 14 in. Area J 25 in. 2 12. 000 πr 2 Area of a circle = _______ A = π(0. 625)2 Board A = 1. 227 Length _______ 3 in 1. 227 14. 454

Measurement 200 The net of a cube is shown below. Use the ruler on the Mathematics Chart to measure the dimensions of the cube to the nearest inch. Find the surface area of the cube to the nearest square inch. A 2 in. 2 B 9 in. 2 C 14 in. 2 D 18 in. 2 Board Answer

Measurement 200 The net of a cube is shown below. Use the ruler on the Mathematics Chart to measure the dimensions of the cube to the nearest inch. Find the surface area of the cube to the nearest square inch. A 2 in. 2 B 9 in. 2 C 14 in. 2 D 18 in. 2 Board

Measurement 200 The net of a cube is shown below. Use the ruler on the Mathematics Chart to measure the dimensions of the cube to the nearest inch. Find the surface area of the cube to the nearest square inch. A 2 in. 2 B 9 in. 2 C 14 in. 2 D 18 in. 2 Board

Measurement 200 The net of a cube is shown below. Use the ruler on the Mathematics Chart to measure the dimensions of the cube to the nearest inch. Find the surface area of the cube to the nearest square inch. A 2 in. 2 B 9 in. 2 2. 25 in 2 C 14 in. 2 D 18 in. 2 Board 2. 25 in 2

Measurement 300 The net of a cylinder is shown below. Use the ruler on the Mathematics Chart to measure the dimensions of the cylinder to the nearest tenth of a centimeter. Find the total surface area of this cylinder to the nearest square centimeter. F 6 cm 2 G 14 cm 2 H 19 cm 2 J 33 cm 2 Board Answer

Measurement 300 2 cm The net of a cylinder is shown below. Use the ruler on the Mathematics Chart to measure the dimensions of the cylinder to the nearest tenth of a centimeter. Find the total surface area of this cylinder to the nearest square centimeter. F 6 cm 2 Rect. = 18. 8 cm 2 1. 5 cm G 14 cm 2 Circle = 7. 1 cm 2 9. 4 cm H 19 cm 2 Circle = 7. 1 cm 2 33. 0 cm 2 J 33 cm 2 Board

Measurement 400 The net of a cylinder is shown below. Use the ruler on the Math Chart to measure the dimensions of the cylinder to the nearest tenth of a centimeter. Which of the following best represents the total surface area of this cylinder? F 142 cm 2 G 93 cm 2 H 23 cm 2 J 14 cm 2 Board Answer

Measurement 400 10. 5 cm The net of a cylinder is shown below. Use the ruler on the Math Chart to measure the dimensions of the cylinder to the nearest tenth of a centimeter. Which of the following best 7 cm represents the total surface 1. 7 cm area of this cylinder? F 142 cm 2 Rect. = 73. 5 cm 2 G 93 cm 2 Circle = 9. 1 cm 2 H 23 cm 2 91. 7 cm 2 J 14 cm Board

Measurement 500 Use the ruler on the Mathematics Chart to measure the dimensions of the composite figure to the nearest tenth of a centimeter. Which best represents the approximate area of this composite figure? A 34. 7 cm 2 B 38. 8 cm 2 C 44. 6 cm 2 D 54. 5 cm 2 Board Answer

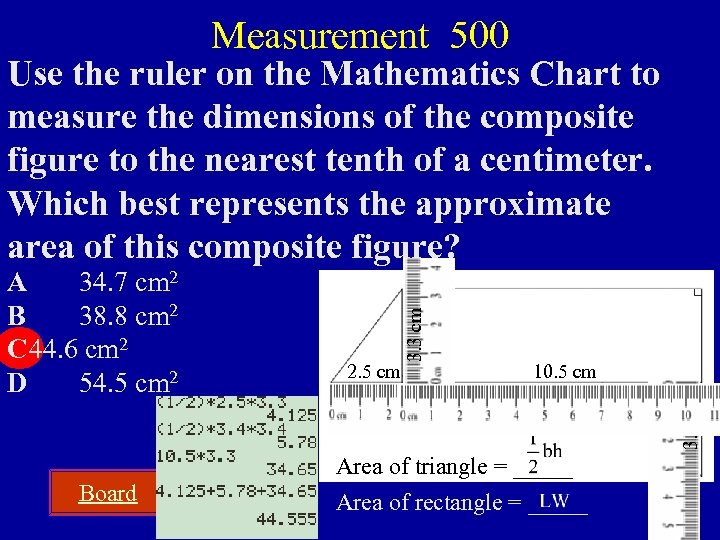Measurement 500 Board 2. 5 cm 10. 5 cm Area of triangle = _____ Area of rectangle = _____ 3. 4 cm A 34. 7 cm 2 B 38. 8 cm 2 C 44. 6 cm 2 D 54. 5 cm 2 3. 3 cm Use the ruler on the Mathematics Chart to measure the dimensions of the composite figure to the nearest tenth of a centimeter. Which best represents the approximate area of this composite figure?

Dilations and Measurements 100 The scale of two similar quadrilaterals is 1: 2. The perimeter of the smaller quadrilateral is 80 centimeters. What is the perimeter of the larger quadrilateral? A 40 cm B 80 cm C 160 cm D 320 cm Board Answer

Dilations and Measurements 100 The scale of two similar quadrilaterals is 1: 2. The perimeter of the smaller quadrilateral is 80 centimeters. What is the perimeter of the larger quadrilateral? Pick a rectangle with a perimeter of 80 cm A 40 cm 30 cm B 80 cm Area = 300 cm 2 10 cm C 160 cm Create a rectangle twice as big D 320 cm 60 cm Board Perimeter = 160 cm Area = 1200 cm 2 The area is 4 times as big 20 cm

Dilations and Measurements 200 The scale factor of two similar polygons is 2: 3. The perimeter of the larger polygon is 150 centimeters. What is the perimeter of the smaller polygon? A 100 cm B 75 cm C 50 cm D 150 cm Board Answer

Dilations and Measurements 200 The scale factor of two similar polygons is 2: 3. The perimeter of the larger polygon is 150 centimeters. What is the perimeter of the smaller Pick a rectangle with a perimeter of 150 cm polygon? 60 cm A 100 cm Area = 900 cm 2 B 75 cm 15 cm C 50 cm D 150 cm Create a rectangle 2/3 as big Board 40 cm Perimeter = 100 cm 10 cm 2 Area = 400 cm The area is as big

Dilations and Measurements 300 Tony and Edwin each built a rectangular garden. Tony’s garden is twice as long and twice as wide as Edwin’s garden. If the area of Edwin’s garden is 600 square feet, what is the area of Tony’s garden? A 1200 ft 2 B 2400 ft 2 C 3600 ft 2 D 4800 ft 2 Board Answer

Dilations and Measurements 300 Tony and Edwin each built a rectangular garden. Tony’s garden is twice as long and twice as wide as Edwin’s garden. If the area of Edwin’s garden is 600 square feet, what is the area of Tony’s Pick a rectangle with an area of 600 ft 2 garden? 30 ft A 1200 ft 2 20 ft Per. = 100 ft 2 B 2400 ft Create a rectangle twice as big C 3600 ft 2 60 ft D 4800 ft 2 2 Board Area = 2400 ft (4 times the area) Per. = 200 ft 40 ft The perimeter is twice as big

Dilations and Measurements 400 A rectangular solid has a volume of 24 cubic decimeters. If the length, width, and height are all changed to their original size, what will be the new volume of the rectangular solid? A 3 dm 3 B 4 dm 3 C 6 dm 3 D 12 dm 3 Board Answer

Dilations and Measurements 400 A rectangular solid has a volume of 24 cubic decimeters. If the length, width, and height are all changed to their original size, what will be the new volume of the rectangular solid? A 3 dm 3 Pick a rectangular solid with a volume of 24 dm 3 B 4 dm 3 6 dm C 6 dm 3 D 12 dm 3 2 dm Create a rectangle half as big Board 3 dm 1 dm Vol = 3 dm 3 ( the volume)

Dilations and Measurements 500 If the surface area of a cube is increased by a factor of 4, what is the change in the length of the sides of the cube? F The length is 2 times the original length. G The length is 4 times the original length. H The length is 6 times the original length. J The length is 8 times the original length. Board Answer

Dilations and Measurements 500 If the surface area of a cube is increased by a factor of 4, what is the change in the length of the sides of the cube? F The length is 2 times the original length. 4 Each length 2 times as big makes the area _____ times bigger G The length is 4 times the original length. 16 Each length 4 times as big makes the area _____ times bigger H The length is 6 times the original length. 36 Each length 6 times as big makes the area _____ times bigger J The length is 8 times the original length. 64 Each length 8 times as big makes the area _____ times bigger Board

Proportions 100 Kate has 2 similar triangular pieces of paper, as shown below. Using the dimensions given, find the approximate length of the side labeled p. Board Answer

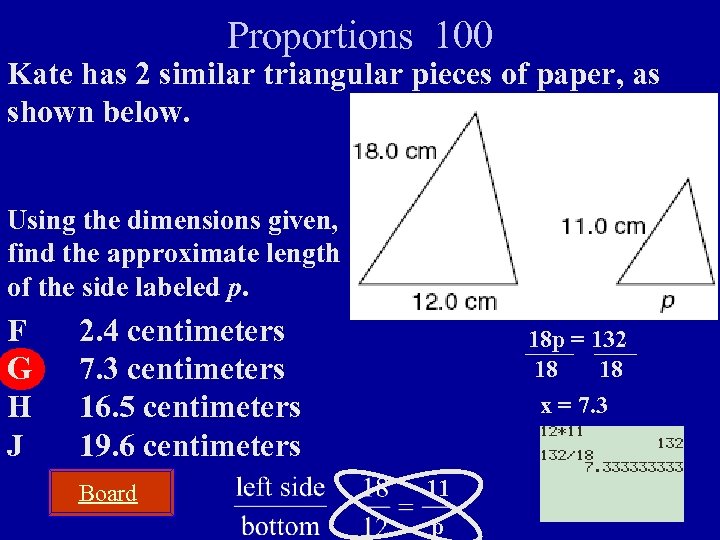Proportions 100 Kate has 2 similar triangular pieces of paper, as shown below. Using the dimensions given, find the approximate length of the side labeled p. F G H J 2. 4 centimeters 7. 3 centimeters 16. 5 centimeters 19. 6 centimeters Board 18 p = 132 18 18 x = 7. 3 11 p

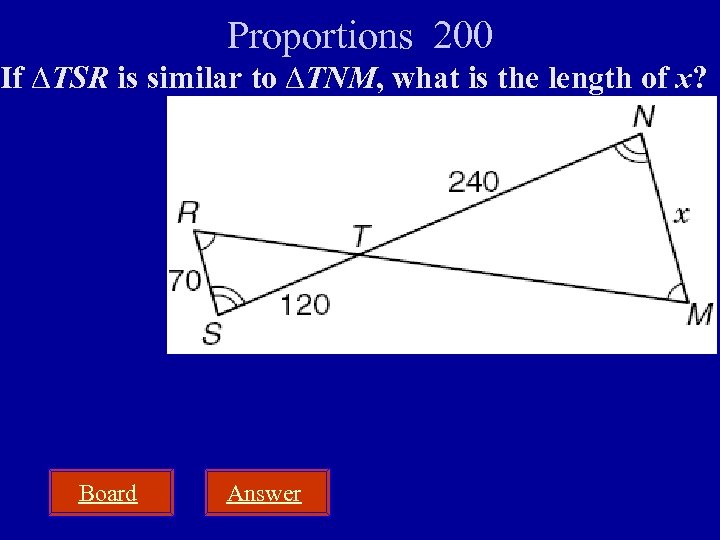Proportions 200 If ∆TSR is similar to ∆TNM, what is the length of x? Board Answer

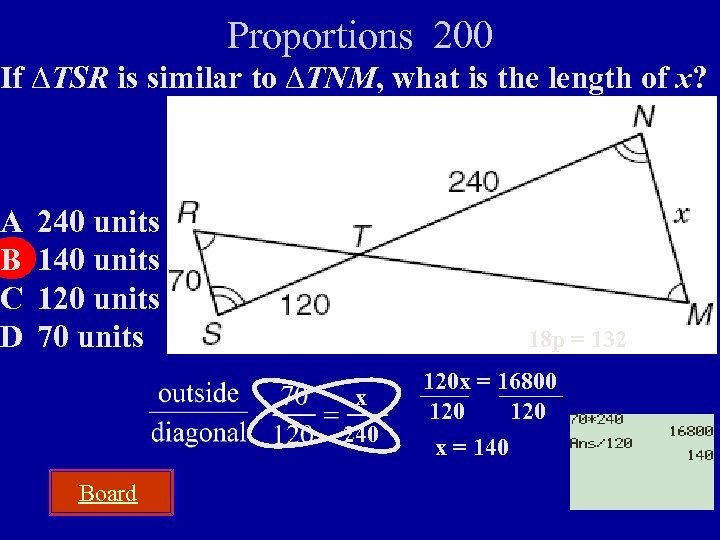Proportions 200 If ∆TSR is similar to ∆TNM, what is the length of x? A B C D 240 units 120 units 70 units 18 p = 132 x 240 Board 120 x = 16800 120 x = 140

Proportions 300 A certain parallelogram has the dimensions shown. Which set of dimensions would produce a similar figure? F 17. 6 cm, 88 cm G 70. 4 cm, 176 cm H 105. 6 cm, 132 cm J 140. 8 cm, 220 cm Board Answer

Proportions 300 A certain parallelogram has the dimensions shown. Which set of dimensions would produce a similar figure? F 17. 6 cm, 88 cm G 70. 4 cm, 176 cm H 105. 6 cm, 132 cm J 140. 8 cm, 220 cm 70. 4, 88 (35. 2 cm, 44 cm) 2 = _____ 140. 8, 176 (35. 2 cm, 44 cm) 4 = _____ Board 105. 6, 132 (35. 2 cm, 44 cm) 3 = _____

Proportions 400 To estimate the height of her school’s gym, Nicole sights the top of the gym wall in a mirror that she has placed on the ground. The mirror is 3. 6 meters from the base of the gym wall. Nicole is standing 0. 5 meter from the mirror, and her height is about 1. 8 meters. What is the height of the gym wall? Board Answer

Proportions 400 To estimate the height of her school’s gym, Nicole sights the top of the gym wall in a mirror that she has placed on the ground. The mirror is 3. 6 meters from the base of the gym wall. Nicole is standing 0. 5 meter from the mirror, and her height is about 1. 8 meters. What is the height of the gym wall? F 1 m G 5. 9 m H 7. 2 m J 12. 96 m Board x 3. 6 0. 5 x = 6. 48 0. 5 x = 12. 96

Proportions 500 In El Paso, Texas, the streets named Hercules Avenue, Hondo Pass Drive, and Trans Mountain Road are parallel. They all intersect Dyer Street and U. S. Route 54, as shown on the map below. If all of these streets are straight line segments, how long is Dyer Street between Hercules Avenue and Trans Mountain Road? Board Answer

Proportions 500 In El Paso, Texas, the streets named Hercules Avenue, Hondo Pass Drive, and Trans Mountain Road are parallel. They all intersect Dyer Street and U. S. Route 54, as shown on the map below. If all of these streets are straight line segments, how long is Dyer Street between Hercules Avenue and Trans Mountain Road? 10560 A 8, 450 ft x B 9, 900 ft 5280 x = 69696000 C 13, 200 ft 5280 D 19, 800 ft Board x = 13, 200

Geometric Problem Solving 100 The map below shows 2 different routes Ms. Bentsen can take to drive to the airport from her house. How many miles could Ms. Bentsen save by traveling on Airport Road instead of Mountain Highway and Oak Road to get to the airport? Board Answer

Geometric Problem Solving 100 The map below shows 2 different routes Ms. Bentsen can take to drive to the airport from her house. How many miles could Ms. Bentsen save by traveling on Airport Road instead of Mountain Highway and Oak Road to get to the airport? a 2 + b 2 = c 2 A 20 mi 252 + b 2 = 652 B 30 mi 625 + b 2 = 4225 -625 C 35 mi b 2 = 3600 60 mi D 60 mi b = 60 Board Distance = _____ 85 mi Distance saved = _____ 20 mi

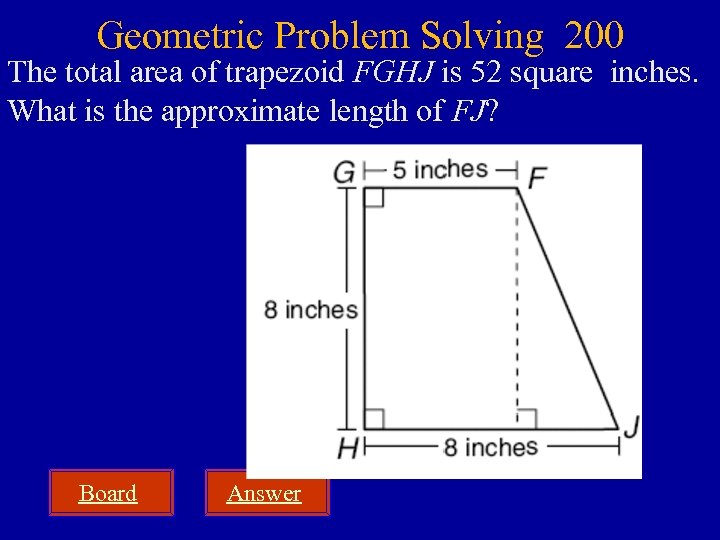Geometric Problem Solving 200 The total area of trapezoid FGHJ is 52 square inches. What is the approximate length of FJ? Board Answer

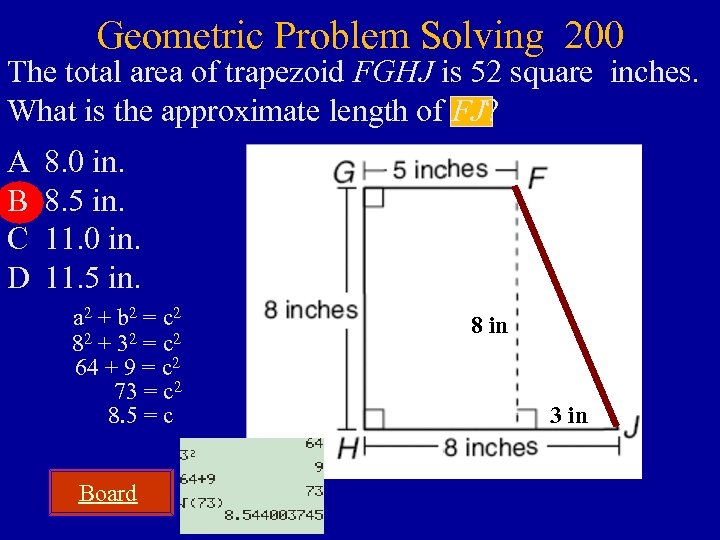Geometric Problem Solving 200 The total area of trapezoid FGHJ is 52 square inches. What is the approximate length of FJ? A B C D 8. 0 in. 8. 5 in. 11. 0 in. 11. 5 in. a 2 + b 2 = c 2 82 + 32 = c 2 64 + 9 = c 2 73 = c 2 8. 5 = c Board 8 in 3 in

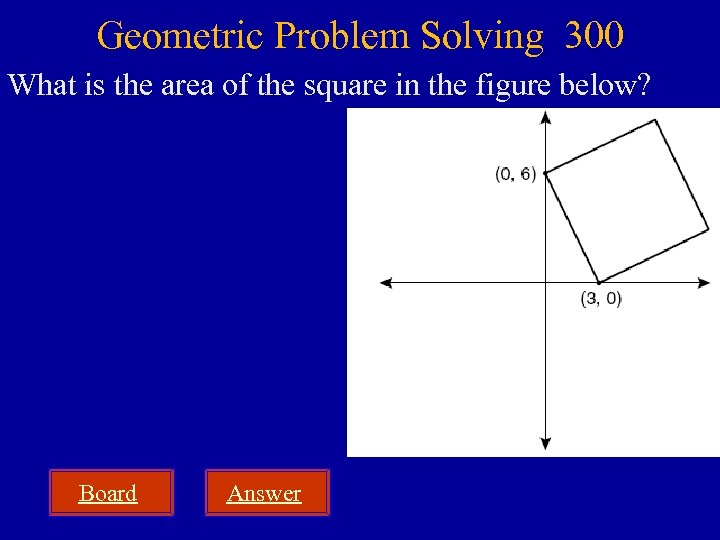Geometric Problem Solving 300 What is the area of the square in the figure below? Board Answer

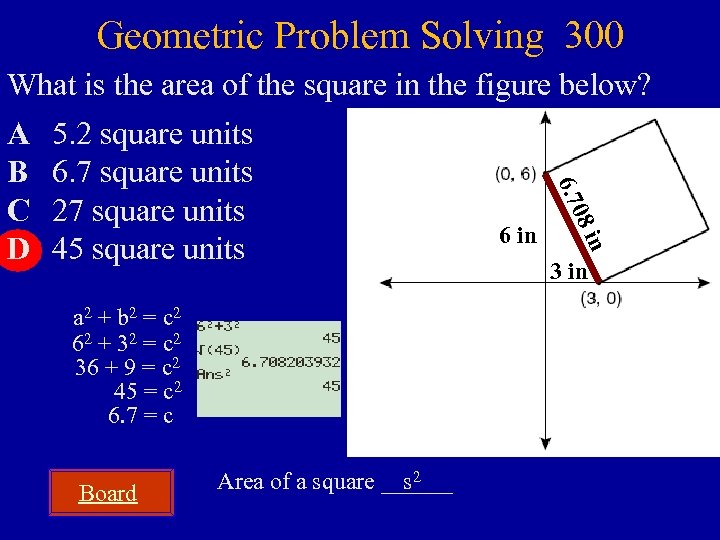Geometric Problem Solving 300 What is the area of the square in the figure below? Board Area of a square ______ s 2 in a 2 + b 2 = c 2 62 + 32 = c 2 36 + 9 = c 2 45 = c 2 6. 7 = c 6 in 08 5. 2 square units 6. 7 square units 27 square units 45 square units 6. 7 A B C D 3 in

Geometric Problem Solving 400 The shaded area in the circle below represents the section of a park used by the chamber of commerce for a fund-raising event. What is the approximate area of the section of the park used for the fund-raiser? Board Answer

Geometric Problem Solving 400 The shaded area in the circle below represents the section of a park used by the chamber of commerce for a fund-raising event. What is the approximate area of the section of the park used for the fund-raiser? F G H J 339 square feet 1, 357 square feet 4, 071 square feet 12, 214 square feet Board

Geometric Problem Solving 500 A frozen dinner is divided into 3 sections on a circular plate with a 12 -inch diameter. What is the approximate length of the arc of the section containing peas? Board Answer

Geometric Problem Solving 500 A frozen dinner is divided into 3 sections on a circular plate with a 12 -inch diameter. What is the approximate length of the arc of the section containing peas? F 3 in. G 21 in. H 16 in. J 5 in. Board

Final Jeopardy Category Board

Final Jeopardy Question In ∆STR, and are parallel If SQ = 6 units, QT = 24 units, and the perimeter of ∆SQP is 20 units, what is the perimeter of ∆STR? Answer

Final Jeopardy Answer In ∆STR, and are parallel 24 6 If SQ = 6 units, QT = 24 units, and the perimeter of ∆SQP is 20 units, what is the perimeter of ∆STR? A B C D 80 units 100 units 320 units 500 units 30 How long is ST? _______ How many times bigger is the 5 larger triangle? _______ Board 5 The perimeter is how many times larger? _______