Tolkynay lesson plan.pptx
- Количество слайдов: 12

Lesson plan

Students will able to: Recognize and write the fundamental trigonometric identities 2. Use the fundamental trigonometric identities to evaluate trigonometric functions, simplify trigonometric expressions, and rewrite trigonometric expressions 3. Express the fundamental identities in alternate forms. 1.

Two important identities that must be learnt are: sin 2θ + cos 2θ ≡ 1 The symbol ≡ means “is identically equal to” although an equals sign can also be used. An identity, unlike an equation, is true for every value of the given variable so, for example: sin 24° + cos 24° ≡ 1, sin 267° + cos 267° ≡ 1, sin 2π + cos 2π ≡ 1, etc.

We can prove these identities by considering a right-angled triangle: r y θ x Also: But by Pythagoras’ theorem x 2 + y 2 = r 2 so:

Pythagorean Identities Even/Odd Identities

Cofunction Identities
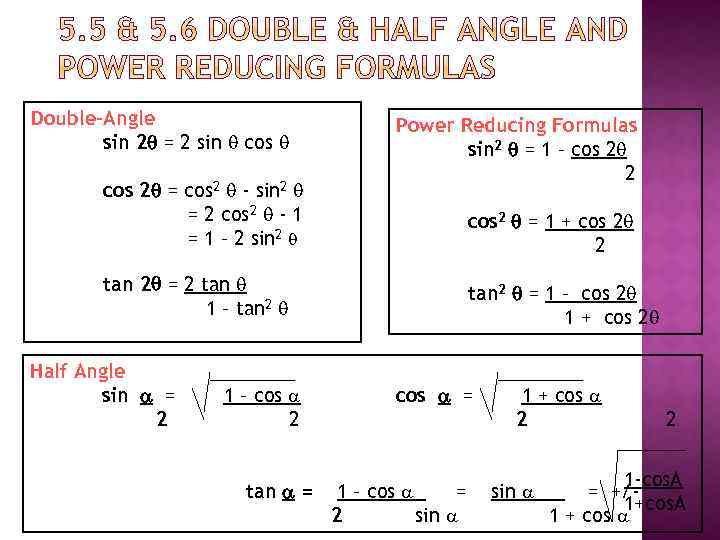
Double-Angle sin 2 = 2 sin cos 2 = cos 2 - sin 2 = 2 cos 2 - 1 = 1 – 2 sin 2 Power Reducing Formulas sin 2 = 1 – cos 2 2 cos 2 = 1 + cos 2 2 tan 2 = 2 tan 1 – tan 2 Half Angle sin = 2 1 – cos 2 tan = tan 2 = 1 – cos 2 1 + cos 2 cos = 1 – cos = 2 sin 1 + cos 2 sin 2 1 -cos. A = +/1+cos. A 1 + cos

Product to Sum sin = ½ [cos ( - ) – cos ( + )] cos = ½ [cos ( - ) + cos ( + )] sin cos = ½ [sin ( + ) + sin ( - )] cos sin = ½ [cos ( + ) – sin ( - )] Sum to Product sin + sin = 2 sin + cos - 2 2 sin - sin = 2 sin - cos + 2 2 cos + cos = 2 cos + cos - 2 2 cos - cos = -2 sin + sin - 2 2

Example: If and Ө is in quadrant II, find each function value. (Cont. ) n b) sin Ө Tip: Use Quotient Identities. n c) cot (- Ө ) Tip: Use Reciprocal and Negative-Angle Identities. 9


Identity – An equation that is satisfied for all meaningful replacements of the Verifying Identities – Show/Prove one side of an equation actually equals th Example: Verify the identity: Techniques for Verifying Identitie 1. Change to Sine and Cosine cot + 1 = csc (cos + sin ) = 1/sin (cos + sin ) 2. = (1/sin ) cos + (1/sin ) sin = cos / sin + sin / sin 3. = cot + 1 4. We will do other examples in class Use Algebraic Skills – factoring Use Pythagorean Identities Work each side separately (Do NOT add to both sides, etc 5. For 1 – sin x, try multiplying numerator & denominator by 1 + sin x to obtain 1 = sin 2 x

Tolkynay lesson plan.pptx