Lesson Menu Five-Minute Check over Lesson 4 1

Lesson Menu Five-Minute Check (over Lesson 4– 1) Mathematical Practices Then/Now New Vocabulary Key Concept: Standard Form Example 1: Real World Example: Write and Graph an Equation in Standard Form Key Concept: Point-Slope Form Example 2: Write and Graph an Equation in Point-Slope Form Concept Summary: Writing Equations Example 3: Find an Equation of a Line Example 4: Write Equations in Point-Slope and Standard Forms

Over Lesson 4– 1 Write an equation of the line that passes through (4, 1) and has slope − 2. A. y = 4 x – 2 B. y = – 2 x – 1 C. y = – 2 x + 4 D. y = – 2 x + 9

Over Lesson 4– 1 Write an equation of the line that passes through (− 3, 2) and has slope 5. A. y = 5 x + 17 B. y = 5 x + 2 C. y = 5 x – 3 D. y = 5 x – 15

Over Lesson 4– 1 Write an equation of the line that passes through (1, 6) and (4, 9). A. y = 6 x + 3 B. y = 2 x + 4 C. y = x + 5 D. y = x + 6

Over Lesson 4– 1 Write an equation of the line that passes through (− 4, 4) and (− 3, 7). A. y = − 3 x + 16 B. y = − 3 x – 2 C. y = 3 x + 12 D. y = 3 x + 16

Over Lesson 4– 1 GYMS A gym charges $59 per month plus an initiation fee. The total cost for initiation and one year of membership is $742. 50. Write an equation to find the cost y of initiation and x months of membership. Then find the total cost for 18 months of membership. A. y = 59 x + 34. 5; $1096. 50 B. y = 59 x – 34. 5; $1027. 50 C. y = 34. 5 x + 159; $780 D. y = 34. 5 x + 59; $680

Mathematical Practices 1 Make sense of problems. 4 Model with mathematics. 7 Make use of structure. Content Standards F. IF. 2 Use function notation, evaluate functions for inputs in their domains, and interpret statements that use function notation in terms of a context.

You wrote equations in slope-intercept form. • Write equations of lines in standard form and point-slope form. • Write linear equations in different forms.

• standard form • point-slope form

Write and Graph an Equation in Standard form ENTERTAINMENT You are planning a party. Party favors cost $6 each and balloons cost $4. 50 each. You have $90 to spend. A. Write an equation in standard form that models the number of party favors and balloons that you could buy. Let x be the number of party favors and let y be the number of balloons. Write an algebraic expression for the cost of the favors and the balloons.

Write and Graph an Equation in Standard form Party favors cost $6 each and balloons cost $4. 50 each. The total is $90, so make an equation from your expression. Answer: 6. 00 x + 4. 50 y = 90

Write and Graph an Equation in Standard form ENTERTAINMENT You are planning a party. Party favors cost $6 each and balloons cost $4. 50 each. You have $90 to spend. B. Use the intercepts to graph the equation. Find the x-intercept. 6. 00 x + 4. 50(0) = 90 6 x = 90 x = 15 The x-intercept is (15, 0)

Write and Graph an Equation in Standard form Find the y-intercept. 6. 00(0) + 4. 50 y = 90 4. 5 y = 90 y = 20 The y-intercept is (0, 20) Use the intercepts to graph the function.

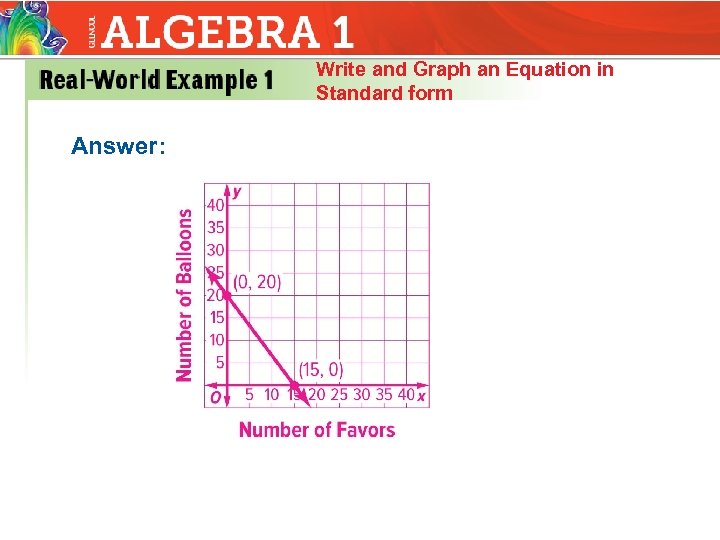Write and Graph an Equation in Standard form Answer:

Write and Graph an Equation in Standard form ENTERTAINMENT You are planning a party. Party favors cost $6 each and balloons cost $4. 50 each. You have $90 to spend. C. If you buy 9 party favors, how many balloons could you buy if you spent exactly $90 without tax? 6. 00 x + 4. 50 y = 90 6. 00(9) + 4. 50 y = 90 54 + 4. 5 y = 90 4. 5 y = 36 y=8 Answer: 8 baloons x = party favors and y = balloons Solve for y. Subtract 54 from both sides. Divide by 4. 5.

Write and Graph an Equation in Point-Slope Form Write an Equation in point-slope form for the line that passes through (– 2, 0) with slope of Point-slope form (x 1, y 1) = (– 2, 0) Simplify. Answer:

Write and Graph an Equation in Point-Slope Form Graph the equation Plot the point at (– 2, 0). Use the slope to find another point on the line. Draw a line through the two points. Answer:

Write the point-slope form of an equation for a line that passes through (4, – 3) with a slope of – 2. A. y – 4 = – 2(x + 3) B. y + 3 = – 2(x – 4) C. y – 3 = – 2(x – 4) D. y + 4 = – 2(x – 3)

Find an Equation of a Line Write an equation in point-slope form, slope-intercept form, and standard form for A. line through point (8, 1) with a slope of y – y 1 = m(x – x 1) y– 1= (x – 8) Point-slope form of the line. (x 1, y 1) = (8, 1) and m = substitute the values for the point-slope form of the line. y– 1= (x – 8) Solve for y to find the slope-intercept form of the line.

Find an Equation of a Line y– 1= x– 6 Add 1 to both sides of the equation. y= x– 5 Slope-intercept form. 4 y = 3 x – 20 3 x – 4 y = 20 Answer: Clear the fractions. Move the x and the y to one side of the equation to get the standard form of the line.

Find an Equation of a Line Write an equation in point-slope form, slope-intercept form, and standard form for B. line through points (3, 5) and (– 6, – 7) Find the slope of the line using the two points. y– 5= (x – 3) (x 1, y 1) = (3, 5) and m = substitute the values for the point-slope form of the line. y– 5= (x – 3) Solve for y to find the slope-intercept form of the line.

Find an Equation of a Line y– 5= x– 4 Add 5 to both sides of the equation. y= x+1 Slope-intercept form. 3 y = 4 x + 3 4 x – 3 y = – 3 Answer: Clear the fractions. Move the x and the y to one side of the equation to get the standard form of the line.

Write Equations in Point-Slope and Standard Forms A. GEOMETRY The figure shows trapezoid ABCD with bases AB and CD. Write an equation in___ point-slope form for the line containing the side BC.

Write Equations in Point-Slope and Standard Forms Step 1 Find the slope of BC. Slope formula (x 1, y 1) = (4, 3) and (x 2, y 2) = (6, – 2)

Write Equations in Point-Slope and Standard Forms Step 2 You can use either point for (x 1, y 1) in the point-slope form. Using (4, 3) Using (6, – 2) y – y 1 = m(x – x 1)

Write Equations in Point-Slope and Standard Forms B. Write an equation in standard form for the same line. Original equation Distributive Property Add 3 to each side. 2 y = – 5 x + 26 5 x + 2 y = 26 Answer: 5 x + 2 y = 26 Multiply each side by 2. Add 5 x to each side.

A. The figure shows right triangle ABC. Write the point-slope form of the line containing the hypotenuse AB. A. y – 6 = 1(x – 4) B. y – 1 = 1(x + 3) C. y + 4 = 1(x + 6) D. y – 4 = 1(x – 6)

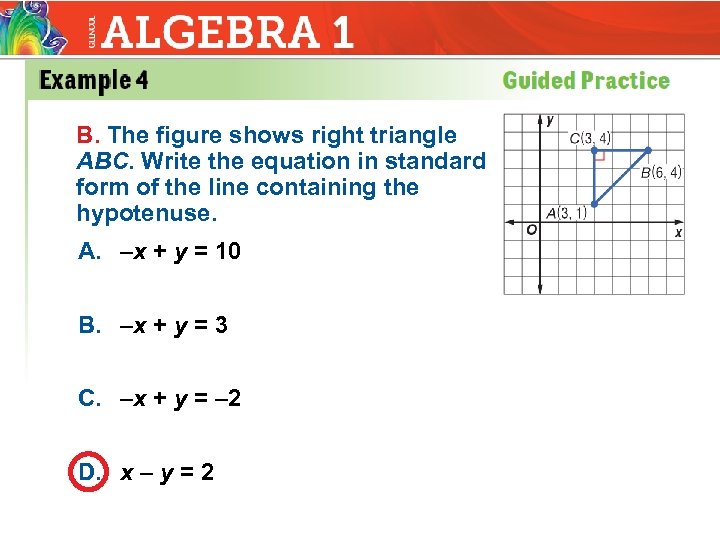B. The figure shows right triangle ABC. Write the equation in standard form of the line containing the hypotenuse. A. –x + y = 10 B. –x + y = 3 C. –x + y = – 2 D. x – y = 2