Lesson 6 7 Fitting Exponential Models to Data

Lesson 6. 7: Fitting Exponential Models to Data • To write exponential equations that model real-world growth and decay data

Victoria Julian has been collecting data on changes in median house prices in her area over the past 10 years. She plans to buy a house 5 years from now and want to know how much money she needs to save each month toward the down payment. How can she make an intelligent prediction of what a house might cost in the future? What assumptions will she have to make?

In the real world, situations like population growth, price inflation, and the decay of substances often tend to approximate an exponential pattern over time. With an appropriate exponential model, you can sometimes predict what might happen in the future. In this lesson you will learn how to find an exponential model to fit data.

Radioactive Decay • Materials Needed ▫ Paper plate ▫ A protractor ▫ A supply of small counters ( about 100 popcorn kernals for each group)

• The particles that make up an atom of some elements, like uranium, are unstable. Over a period of time specific to the element, the particles will change so that the atom eventually will become a different element. This process is called radioactive decay.

• In this investigation your counters represent atoms of a radioactive substance. Draw an angle from the center of your plate, as illustrated. Counters that fall inside the angle represent atoms that have decayed.

• Step 1 ▫ Count the number of counters. Record this in a table as the number of “atoms” after 0 years of decay. Pick up all of the counters. • Step 2 ▫ Drop the counters on the plate. Count and remove the counters that fall inside the angle—these atoms have decayed. Subtract from the previous value and record the number remaining after 1 year of decay. Pick up the remaining counters.

• Step 3 ▫ Repeat step 2 until you have fewer than 10 atoms that have not decayed. Each drop will represent another year of decay. Record the number of atoms remaining each time.

• Step 4 ▫ Let x represent elapsed time in years, and let y represent the number of atoms remaining. Make a scatter plot of the data. What do you notice about the graph? • Step 5 ▫ Calculate the ratio of atoms remaining between successive years. That is, divide the number of atoms after 2 years by the number of atoms after 1 year, and so on. How do these ratios compare?

• Step 6 ▫ Choose one representative ratio. Explain how and why you made your choice. • Step 7 ▫ At what rate did you atoms decay? • Step 8 ▫ Write an exponential equation that models the relationship between time elapsed and the number of atoms remaining.

• Step 9 ▫ Graph the equation with the scatter plot. How well does it fit the data? • Step 10 ▫ If the equation does not fit well, which values could you try to adjust to give a better fit? Record your final equation when you are satisfied.

• Step 11 ▫ Measure the angle on your plate. Describe a connection between your angle and the numbers in your equation. • Step 12 ▫ Based on what you’ve learned and the procedures outline in this investigation, write an equation that would model the decay of 400 counters, using a central angle of 60 o. What are some of the factors that might cause differences between actual data and values predicted by your equation?

Using the steps outlined in this investigation lead to an equation of one of these forms. growth decay

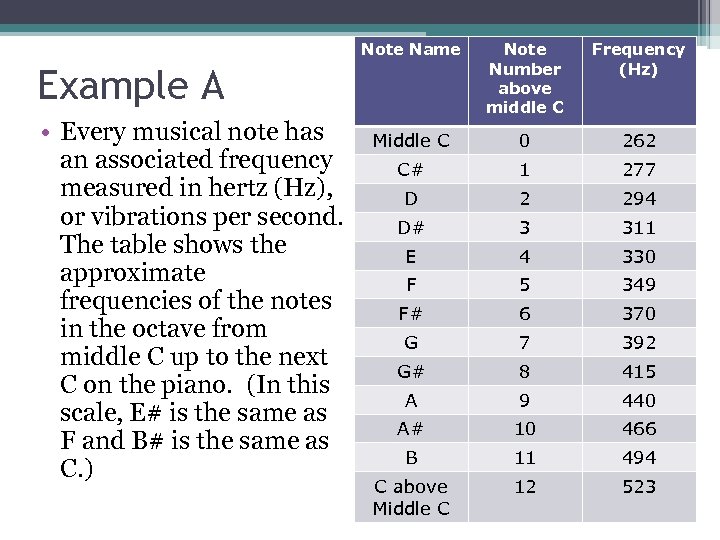Note Name Note Number above middle C Frequency (Hz) Middle C 0 262 C# 1 277 D 2 294 D# 3 311 E 4 330 F 5 349 F# 6 370 G 7 392 G# 8 415 A 9 440 A# 10 466 B 11 494 C above Middle C 12 523 Example A • Every musical note has an associated frequency measured in hertz (Hz), or vibrations per second. The table shows the approximate frequencies of the notes in the octave from middle C up to the next C on the piano. (In this scale, E# is the same as F and B# is the same as C. )

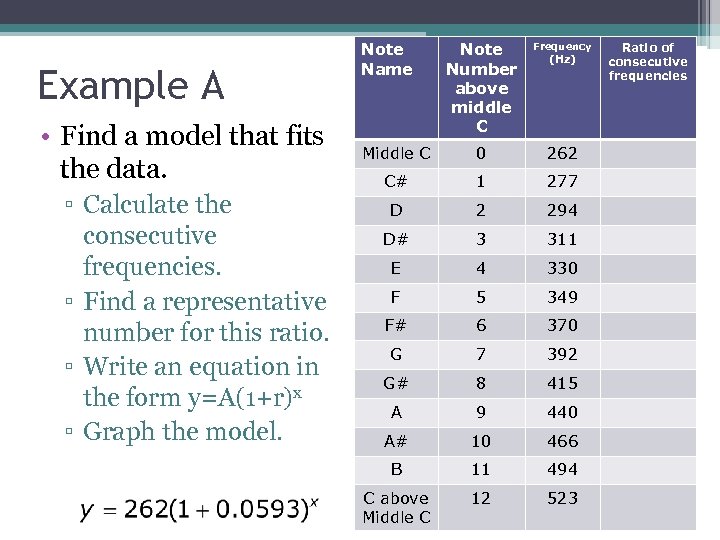Example A • Find a model that fits the data. ▫ Calculate the consecutive frequencies. ▫ Find a representative number for this ratio. ▫ Write an equation in the form y=A(1+r)x ▫ Graph the model. Note Name Note Number above middle C Frequency Middle C 0 262 C# 1 277 D 2 294 D# 3 311 E 4 330 F 5 349 F# 6 370 G 7 392 G# 8 415 A 9 440 A# 10 466 B 11 494 C above Middle C 12 523 (Hz) Ratio of consecutive frequencies

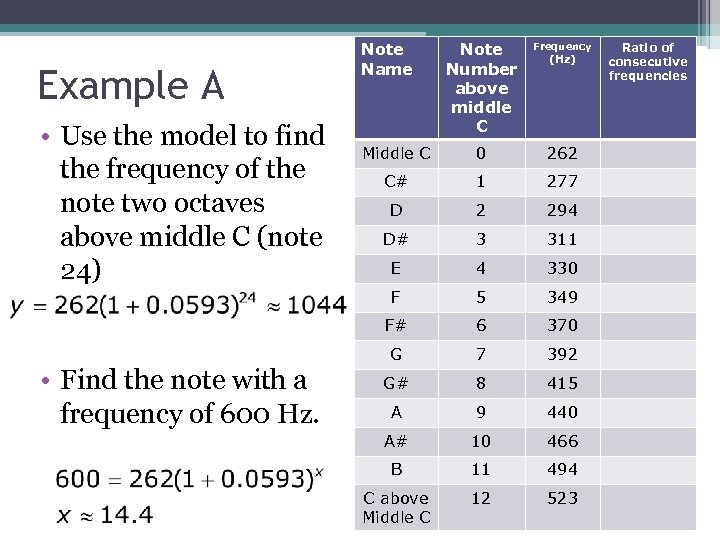• Find the note with a frequency of 600 Hz. Frequency Middle C 0 262 C# 1 277 D 2 294 D# 3 311 E 4 330 5 349 F# • Use the model to find the frequency of the note two octaves above middle C (note 24) Note Number above middle C F Example A Note Name 6 370 G 7 392 G# 8 415 A 9 440 A# 10 466 B 11 494 C above Middle C 12 523 (Hz) Ratio of consecutive frequencies