45c8008e54e2a18bf51995e2a03ae988.ppt
- Количество слайдов: 135
 Les processus métiers : concepts, modèles et systèmes
Les processus métiers : concepts, modèles et systèmes
 Organisation du cours • • • Introduction Concepts et notations Modélisation des processus Analyse qualitative des processus Analyse quantitative des processus Systèmes de gestion de processus Processus transactionnels Découverte de processus Conclusion
Organisation du cours • • • Introduction Concepts et notations Modélisation des processus Analyse qualitative des processus Analyse quantitative des processus Systèmes de gestion de processus Processus transactionnels Découverte de processus Conclusion
 Chapitre 3 : Eléments de modélisation et autres notations
Chapitre 3 : Eléments de modélisation et autres notations
 Contenu (2) • Le chapitre introduit la notion de processus bien structuré et bien parenthésé • Il présente l’essentiel des concepts des modèles UML, Event. Process. Chain et Réseaux de Petri, pour modéliser des processus
Contenu (2) • Le chapitre introduit la notion de processus bien structuré et bien parenthésé • Il présente l’essentiel des concepts des modèles UML, Event. Process. Chain et Réseaux de Petri, pour modéliser des processus
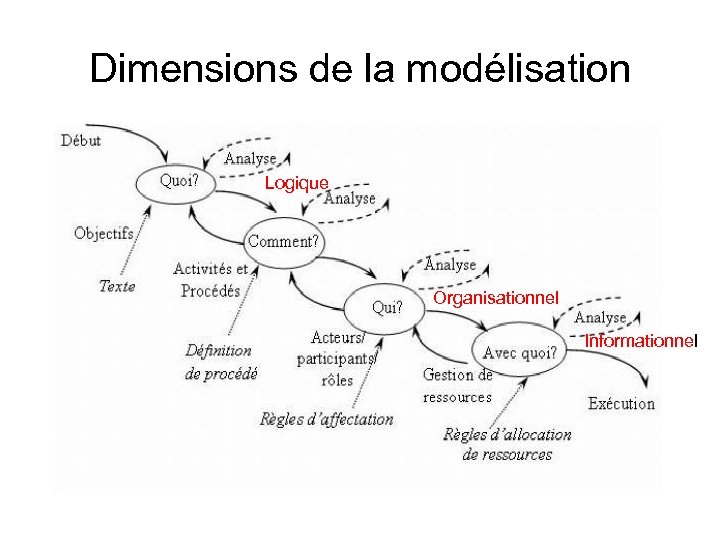 Dimensions de la modélisation Logique Organisationnel Informationnel
Dimensions de la modélisation Logique Organisationnel Informationnel
 Contenu (1) • De fait, il existe assez peu d’approches de modélisation spécifiques aux processus métiers opérationnelles couvrant toutes ces dimensions (voir cependant OSSAD http: //dumas. univtln. fr/Ossad/Appel%20 vol%201. htm ) • Aussi, le chapitre présente plus des notations formelles qu’une méthodologie d’analyse/conception • Mais, le fait de modéliser en se demandant si le processus est bien structuré, bien parenthèse, à choix libre … supporte une discipline de conception efficace
Contenu (1) • De fait, il existe assez peu d’approches de modélisation spécifiques aux processus métiers opérationnelles couvrant toutes ces dimensions (voir cependant OSSAD http: //dumas. univtln. fr/Ossad/Appel%20 vol%201. htm ) • Aussi, le chapitre présente plus des notations formelles qu’une méthodologie d’analyse/conception • Mais, le fait de modéliser en se demandant si le processus est bien structuré, bien parenthèse, à choix libre … supporte une discipline de conception efficace
 Notion de processus bien structuré Bonnes pratiques, mais fondements scientifiques aussi (ex: « Well handled Petri Net)
Notion de processus bien structuré Bonnes pratiques, mais fondements scientifiques aussi (ex: « Well handled Petri Net)
 Notion de processus bien structuré (1) • Un seul point d’entrée et un seul point de sortie • Toute activité est sur un chemin allant du point d’entrée au point de sortie • Les connecteurs de flot de contrôle sont bien parenthésés (AND-Split-AND-Join; XOR-Split, XOR-Join; OR-Split-Jonction …)
Notion de processus bien structuré (1) • Un seul point d’entrée et un seul point de sortie • Toute activité est sur un chemin allant du point d’entrée au point de sortie • Les connecteurs de flot de contrôle sont bien parenthésés (AND-Split-AND-Join; XOR-Split, XOR-Join; OR-Split-Jonction …)
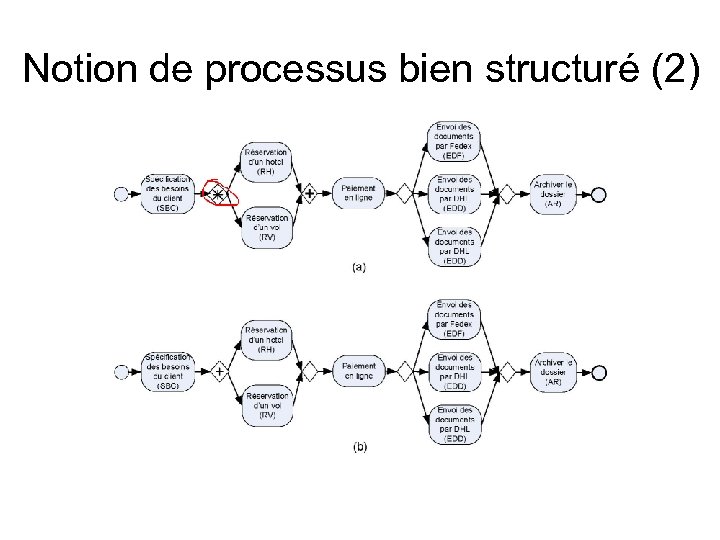 Notion de processus bien structuré (2)
Notion de processus bien structuré (2)
 Notion de processus bien structuré (3) • Dans le cas (a), une parenthèse OR-Split est fermée par une parenthèse AND-Join, il y a risque de blocage : si une seule branche est activée, la porte AND-JOIN n’est jamais franchie – Le graphe de processus contient une « impasse » • Dans le cas (b), une parenthèse AND-Split est fermée par une parenthèse OR-Split. quel est l’interprétation de cet OR-Split ? – Le graphe de processus « manque de synchonisation »
Notion de processus bien structuré (3) • Dans le cas (a), une parenthèse OR-Split est fermée par une parenthèse AND-Join, il y a risque de blocage : si une seule branche est activée, la porte AND-JOIN n’est jamais franchie – Le graphe de processus contient une « impasse » • Dans le cas (b), une parenthèse AND-Split est fermée par une parenthèse OR-Split. quel est l’interprétation de cet OR-Split ? – Le graphe de processus « manque de synchonisation »
![Processus avec blocage (impasse) [SAD 00] Processus avec blocage (impasse) [SAD 00]](https://present5.com/presentation/45c8008e54e2a18bf51995e2a03ae988/image-11.jpg) Processus avec blocage (impasse) [SAD 00]
Processus avec blocage (impasse) [SAD 00]
![Processus avec manque de synchonisation [SAD 00] Processus avec manque de synchonisation [SAD 00]](https://present5.com/presentation/45c8008e54e2a18bf51995e2a03ae988/image-12.jpg) Processus avec manque de synchonisation [SAD 00]
Processus avec manque de synchonisation [SAD 00]
![Processus corrects [SAD 00] Processus corrects [SAD 00]](https://present5.com/presentation/45c8008e54e2a18bf51995e2a03ae988/image-13.jpg) Processus corrects [SAD 00]
Processus corrects [SAD 00]
 Tout processus peut-il être transformé un processus bien structuré ? • (Presque) oui … • Certains ne peuvent être transformés qu’en dupliquant des activités • Il existe des cas non transformables … mais très particuliers
Tout processus peut-il être transformé un processus bien structuré ? • (Presque) oui … • Certains ne peuvent être transformés qu’en dupliquant des activités • Il existe des cas non transformables … mais très particuliers
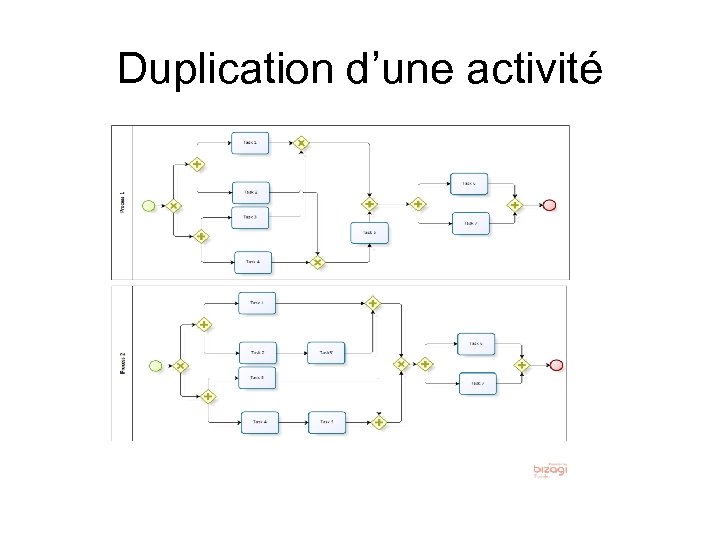 Duplication d’une activité
Duplication d’une activité
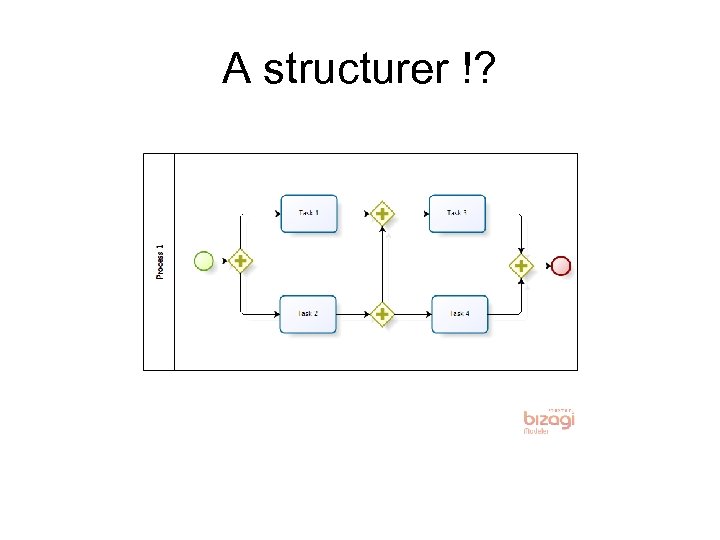 A structurer !?
A structurer !?
 Modéliser avec Unified Modelling Language (UML)
Modéliser avec Unified Modelling Language (UML)
 UML : Principes de modélisation • Ce sont les diagrammes d’activité qui sont au cœur de la modélisation des processus métiers, en particulier du flot de contrôle • Les diagrammes de classes et d’objets sont indispensables à la modélisation des flots de données • Les diagrammes de séquence permettent ici d’étudier les flots de contrôle alternatifs • Mais tous les diagrammes peuvent être utilisés de façon classique, en particulier dans une démarche d’analyse/conception globale d’un logiciel plus large que la modélisation d’un processus
UML : Principes de modélisation • Ce sont les diagrammes d’activité qui sont au cœur de la modélisation des processus métiers, en particulier du flot de contrôle • Les diagrammes de classes et d’objets sont indispensables à la modélisation des flots de données • Les diagrammes de séquence permettent ici d’étudier les flots de contrôle alternatifs • Mais tous les diagrammes peuvent être utilisés de façon classique, en particulier dans une démarche d’analyse/conception globale d’un logiciel plus large que la modélisation d’un processus
 UML Modélisation du flot de contrôle. Les diagrammes d’activité
UML Modélisation du flot de contrôle. Les diagrammes d’activité
 Discordance du vocabulaire • « Processus » « Activité » en UML • « Activité » « Action » en UML
Discordance du vocabulaire • « Processus » « Activité » en UML • « Activité » « Action » en UML
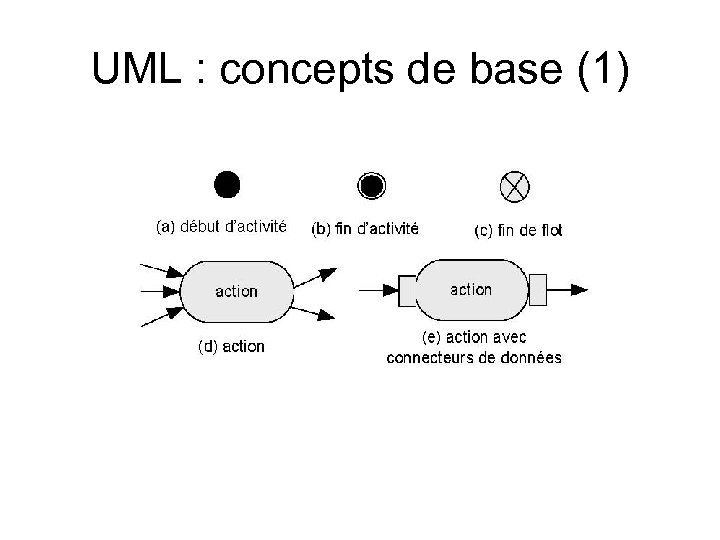 UML : concepts de base (1)
UML : concepts de base (1)
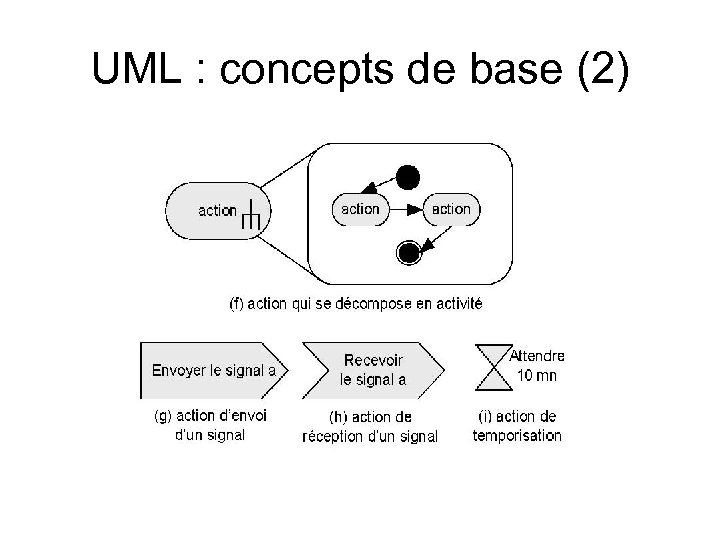 UML : concepts de base (2)
UML : concepts de base (2)
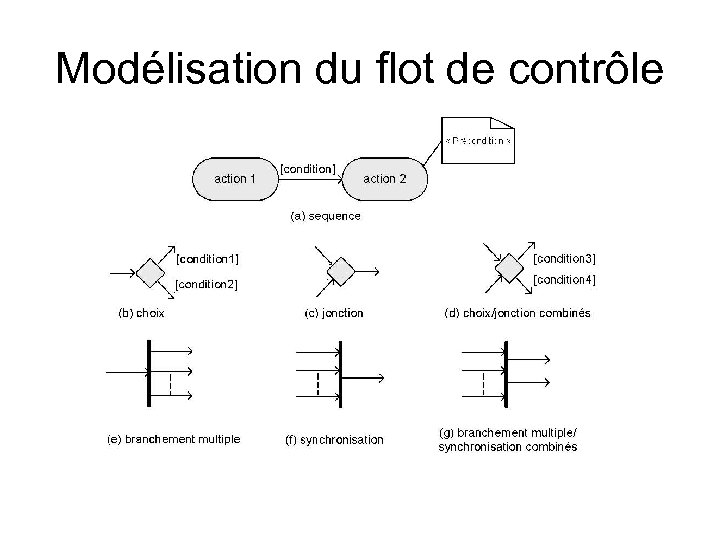 Modélisation du flot de contrôle
Modélisation du flot de contrôle
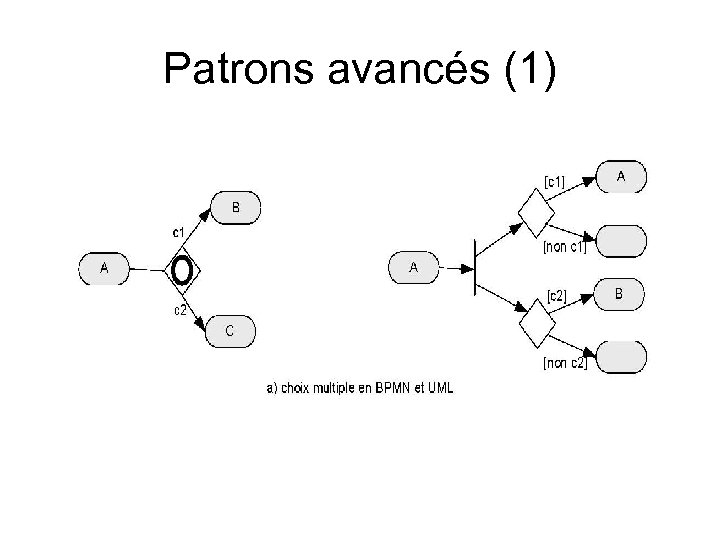 Patrons avancés (1)
Patrons avancés (1)
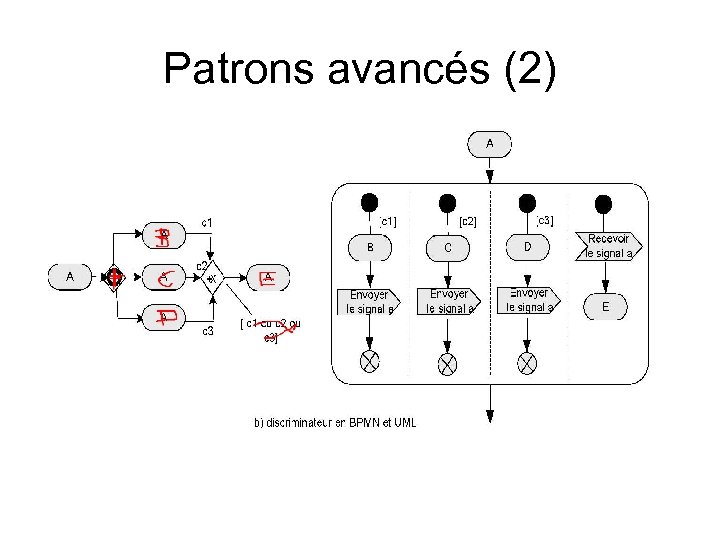 Patrons avancés (2)
Patrons avancés (2)
 UML Modélisation du flot de données
UML Modélisation du flot de données
 Diagramme de classes • Classique … • Indispensable à la modélisation du flot de données • Utilisé pour la méta-modélisation (modélisation des modèles de processus) • Et la modélisation du modèle organisationnel
Diagramme de classes • Classique … • Indispensable à la modélisation du flot de données • Utilisé pour la méta-modélisation (modélisation des modèles de processus) • Et la modélisation du modèle organisationnel
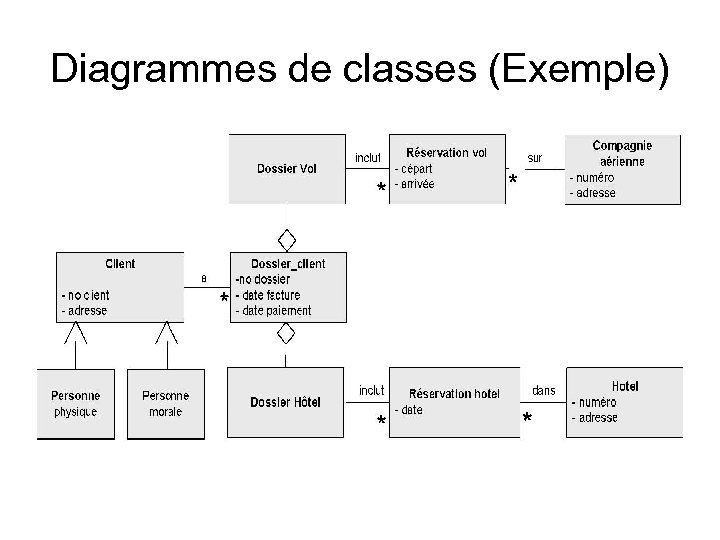 Diagrammes de classes (Exemple)
Diagrammes de classes (Exemple)
 Diagramme de séquence • Les différents scénarios permettent de découvrir les différentes alternatives dans le flot de contrôle
Diagramme de séquence • Les différents scénarios permettent de découvrir les différentes alternatives dans le flot de contrôle
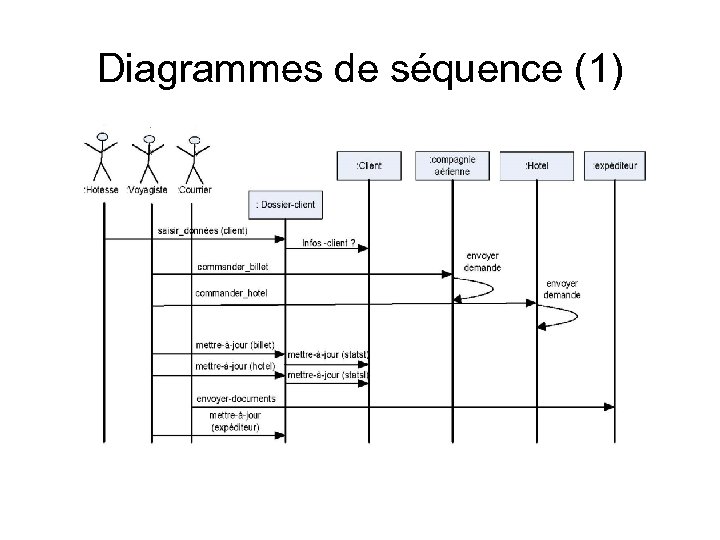 Diagrammes de séquence (1)
Diagrammes de séquence (1)
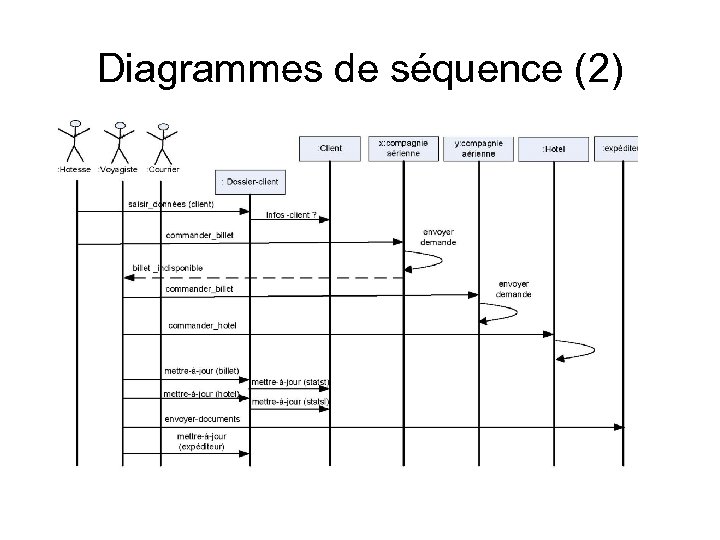 Diagrammes de séquence (2)
Diagrammes de séquence (2)
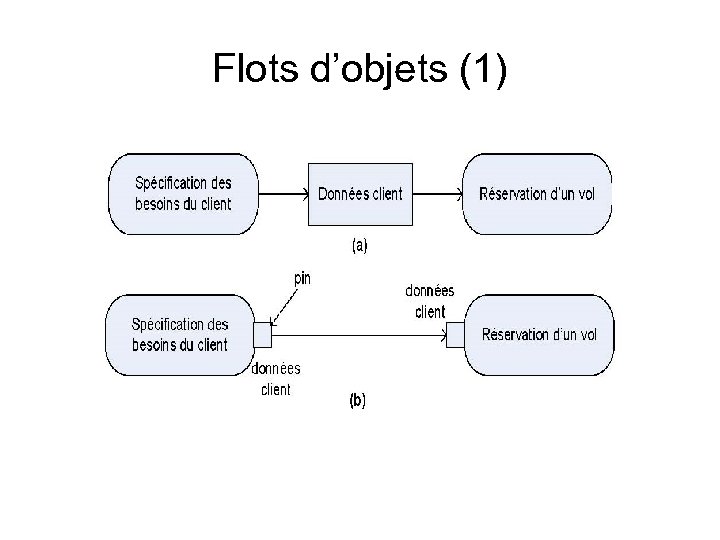 Flots d’objets (1)
Flots d’objets (1)
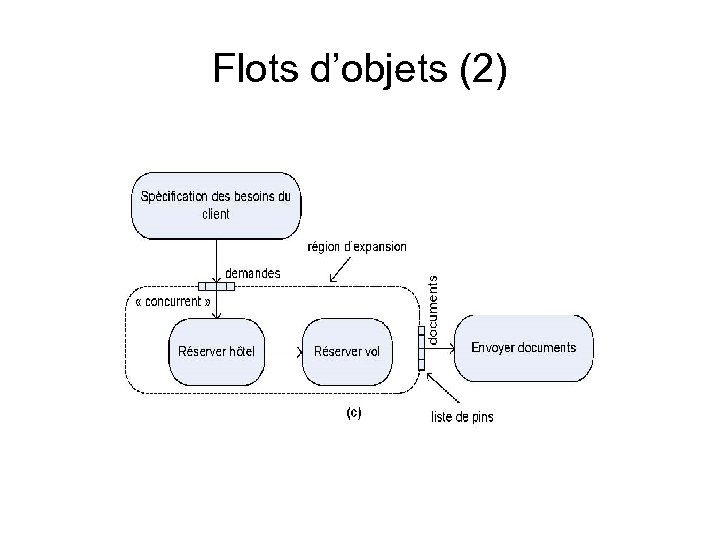 Flots d’objets (2)
Flots d’objets (2)
 UML Modélisation du modèle organisationnel
UML Modélisation du modèle organisationnel
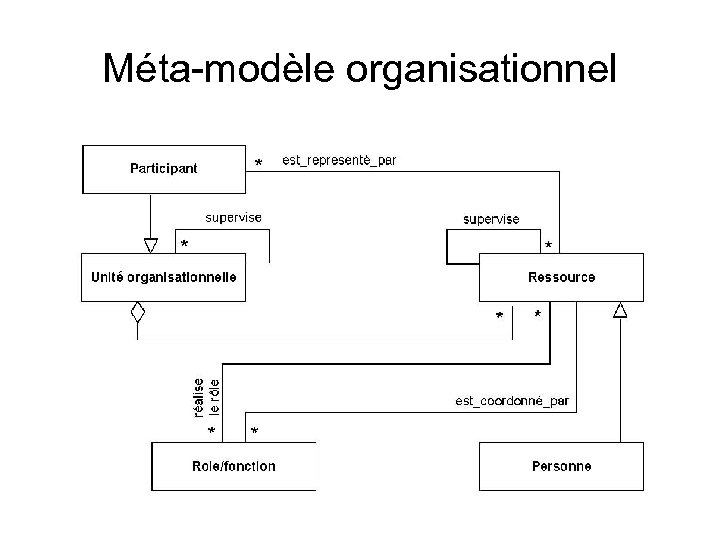 Méta-modèle organisationnel
Méta-modèle organisationnel
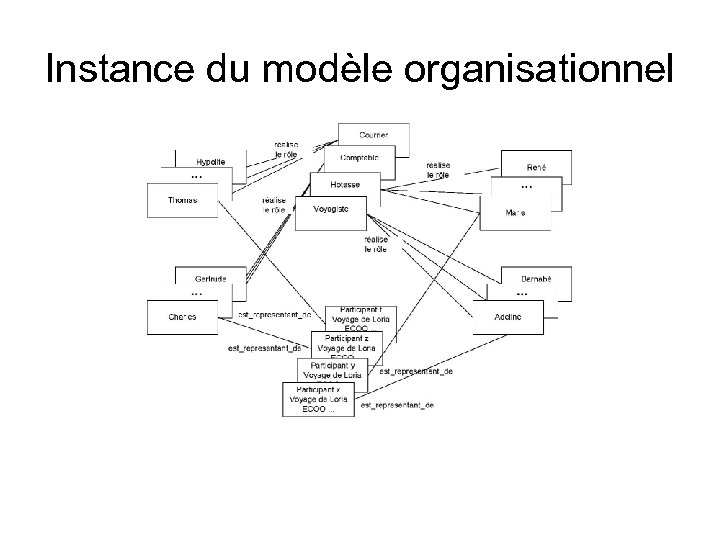 Instance du modèle organisationnel
Instance du modèle organisationnel
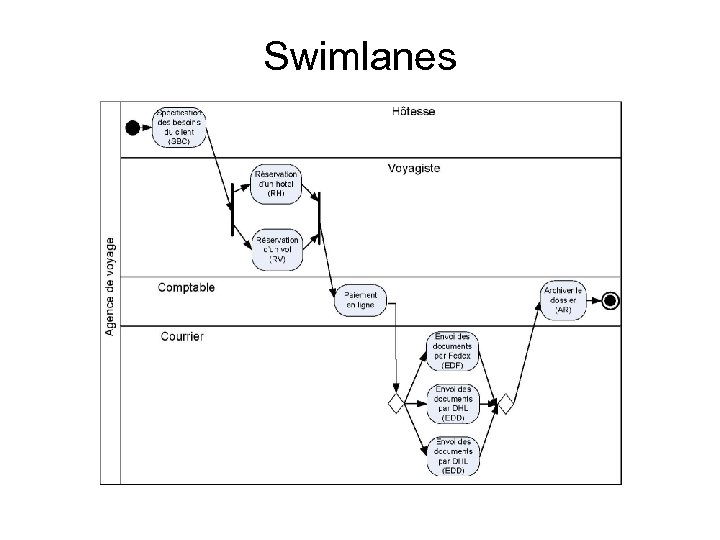 Swimlanes
Swimlanes
 Différentes organisations
Différentes organisations
 Validation • Le processus est-il bien structuré ? • Est-il sain (sans blocage, borné) ? Peu outillé, mais se poser néanmoins la question et utiliser des principes de modélisation qui limite les risques en s’inspirant des Rd. P
Validation • Le processus est-il bien structuré ? • Est-il sain (sans blocage, borné) ? Peu outillé, mais se poser néanmoins la question et utiliser des principes de modélisation qui limite les risques en s’inspirant des Rd. P
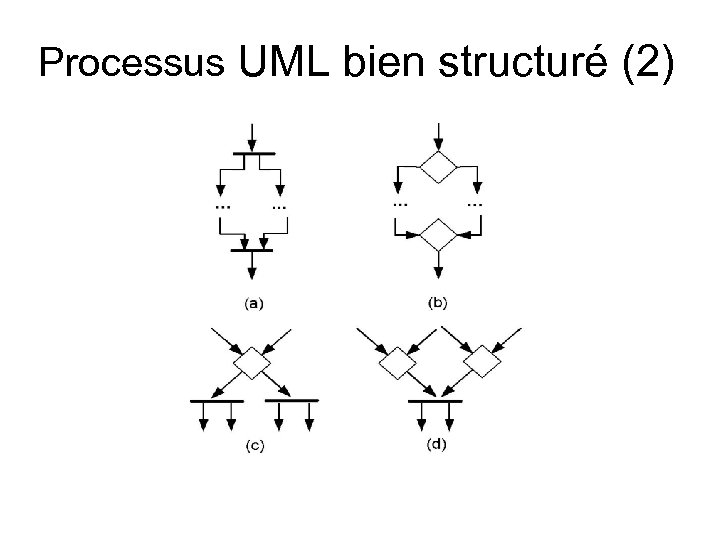 Processus UML bien structuré (2)
Processus UML bien structuré (2)
 Conclusion UML • Moins adapté et outillé que les Rd. P • Mais les diagrammes d’activités empruntent aux Rd. P • Permettent une bonne intégration à l’analyse et à la conception avec les autres aspects d’un logiciel, en particulier dans le contexte de développement orienté objet
Conclusion UML • Moins adapté et outillé que les Rd. P • Mais les diagrammes d’activités empruntent aux Rd. P • Permettent une bonne intégration à l’analyse et à la conception avec les autres aspects d’un logiciel, en particulier dans le contexte de développement orienté objet
 Modéliser avec Event Process Chain (EPC)
Modéliser avec Event Process Chain (EPC)
 Principes de modélisation • 4 perspectives : – Organisationnelle – Donnée – Activité – Contrôle • 3 niveaux d’abstraction – Définition des besoins – Conception – Implantation
Principes de modélisation • 4 perspectives : – Organisationnelle – Donnée – Activité – Contrôle • 3 niveaux d’abstraction – Définition des besoins – Conception – Implantation
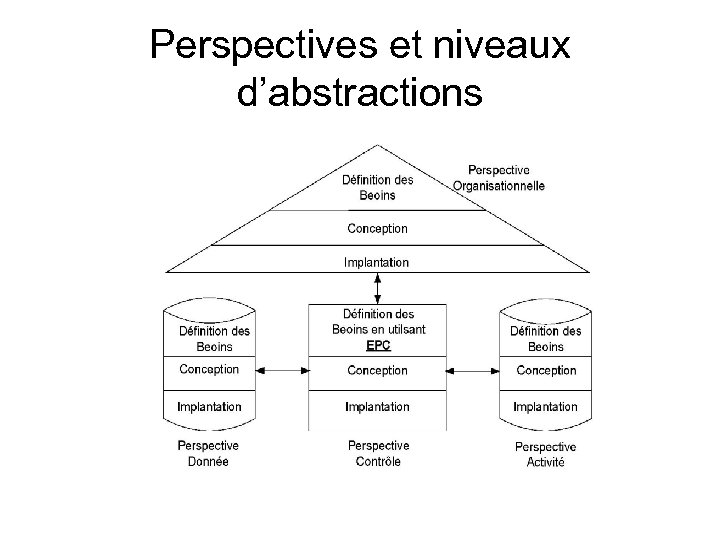 Perspectives et niveaux d’abstractions
Perspectives et niveaux d’abstractions
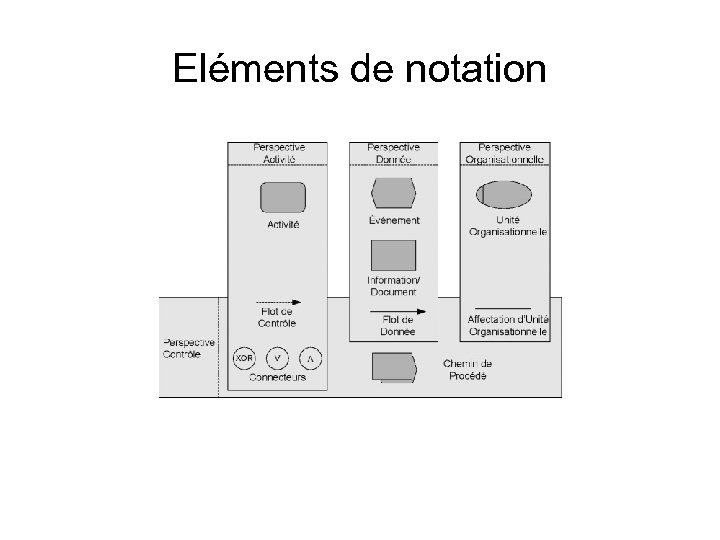 Eléments de notation
Eléments de notation
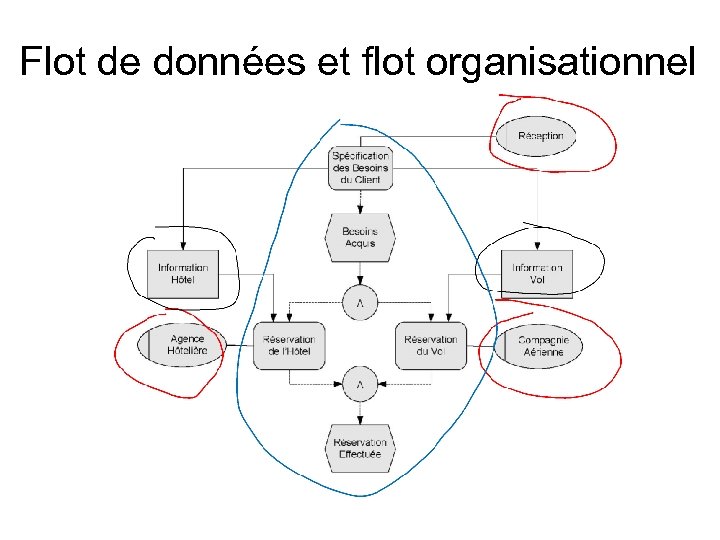 Flot de données et flot organisationnel
Flot de données et flot organisationnel
 Éléments du flot de contrôle • Un modèle EPC est un graphe ordonné d’événements et d’activités alternés et connectés par des connecteurs de flot de contrôle
Éléments du flot de contrôle • Un modèle EPC est un graphe ordonné d’événements et d’activités alternés et connectés par des connecteurs de flot de contrôle
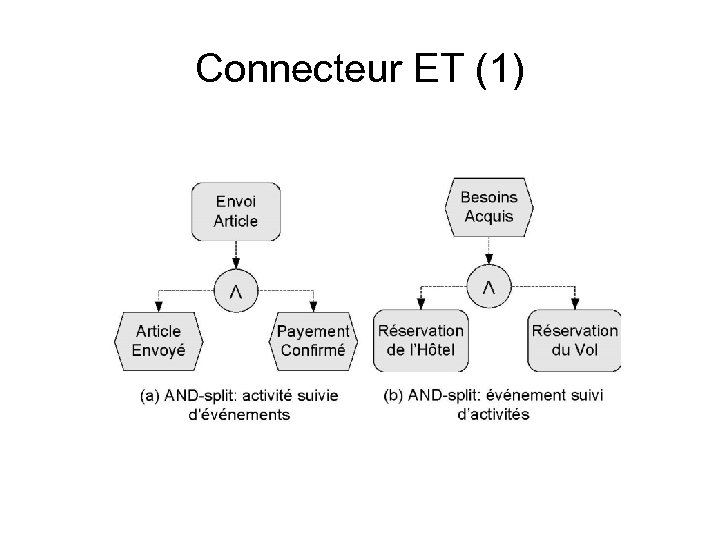 Connecteur ET (1)
Connecteur ET (1)
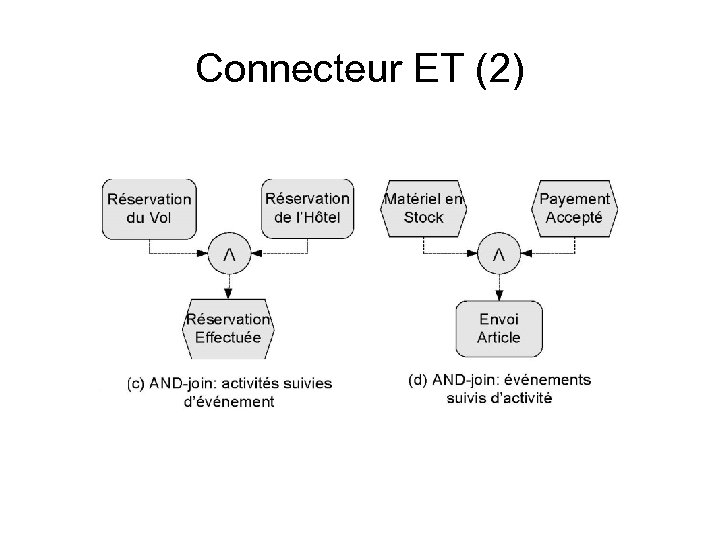 Connecteur ET (2)
Connecteur ET (2)
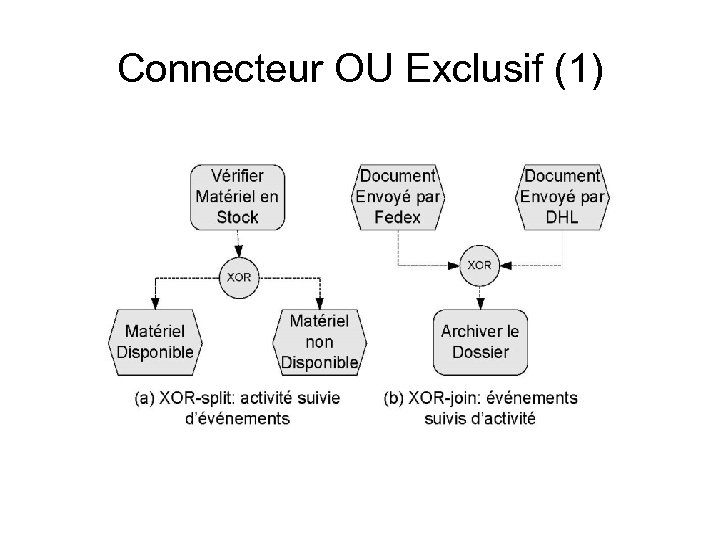 Connecteur OU Exclusif (1)
Connecteur OU Exclusif (1)
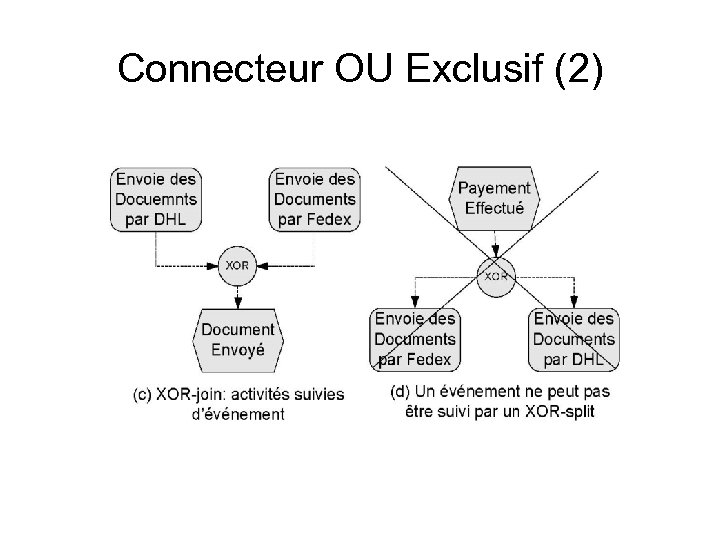 Connecteur OU Exclusif (2)
Connecteur OU Exclusif (2)
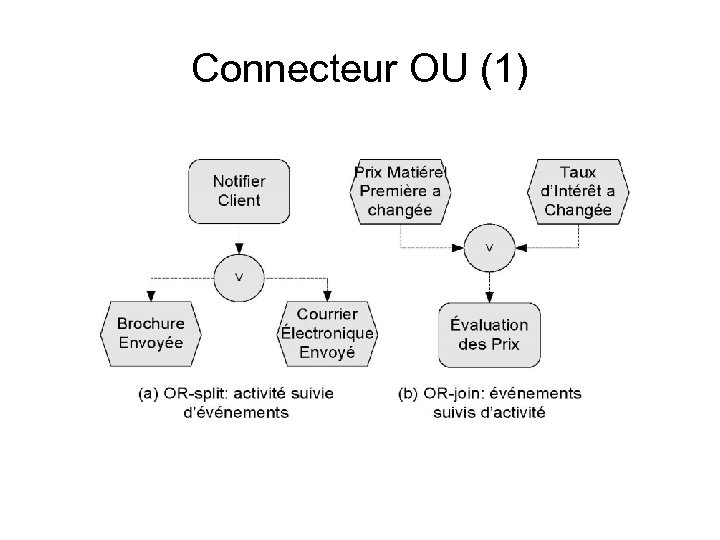 Connecteur OU (1)
Connecteur OU (1)
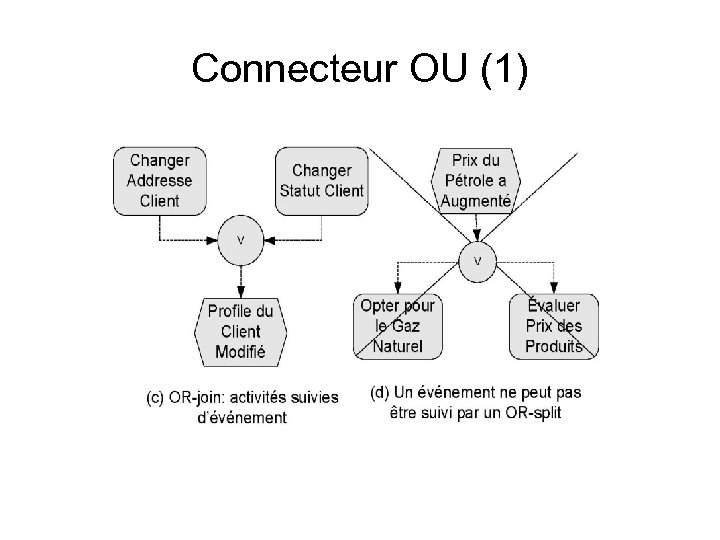 Connecteur OU (1)
Connecteur OU (1)
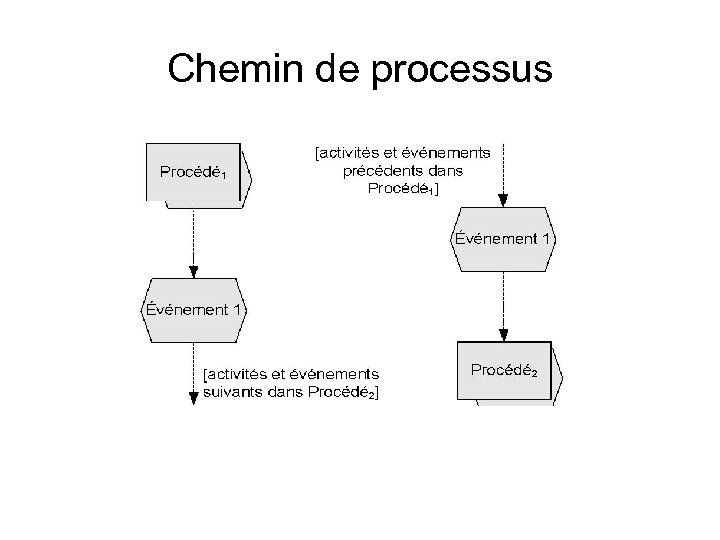 Chemin de processus
Chemin de processus
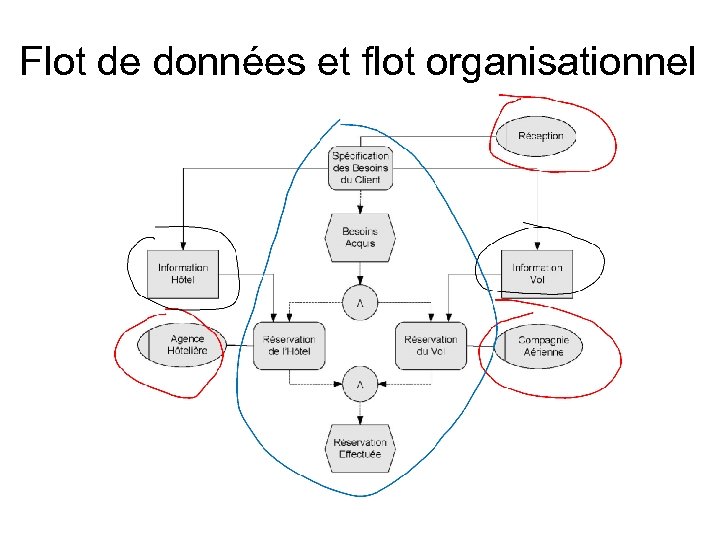 Flot de données et flot organisationnel
Flot de données et flot organisationnel
 Conclusion EPC • Très utilisé dans le monde ERP, SAP • Fondement dans les Rd. P
Conclusion EPC • Très utilisé dans le monde ERP, SAP • Fondement dans les Rd. P
 Modéliser avec des Réseaux de Pétri (Rd. P)
Modéliser avec des Réseaux de Pétri (Rd. P)
 Pourquoi les Rd. P ? • Similarités avec les langages et outils BPM choisi pour développer une sémantique formelle de ces langages (EPC, diagrammes d’activité UML, WS-BPEL) • Fondements mathématiques techniques d’analyse (voir chapitre 4) • Notations graphiques plus facilement accessible à des non spécialistes • Plus implicite et compacte que les modèles à transitions
Pourquoi les Rd. P ? • Similarités avec les langages et outils BPM choisi pour développer une sémantique formelle de ces langages (EPC, diagrammes d’activité UML, WS-BPEL) • Fondements mathématiques techniques d’analyse (voir chapitre 4) • Notations graphiques plus facilement accessible à des non spécialistes • Plus implicite et compacte que les modèles à transitions
 Notion de réseau de Petri
Notion de réseau de Petri
 Définition On appelle réseau de Petri places/transition tout triplet N = (P, T, W) où : – P est un ensemble fini de places : P = {p 1, …, pn} – T est un ensemble fini de transitions, disjoint de P : T = {t 1, … , tm} – W : Px. T U Tx. P N (entiers naturels) est la fonction de valuation des arcs Graphiquement, par convention, les arcs de valuation nulle ne sont pas représentés; les valuations égales à 1 sont omises (valeur par défaut); dans les autres cas, les valuations sont explicites.
Définition On appelle réseau de Petri places/transition tout triplet N = (P, T, W) où : – P est un ensemble fini de places : P = {p 1, …, pn} – T est un ensemble fini de transitions, disjoint de P : T = {t 1, … , tm} – W : Px. T U Tx. P N (entiers naturels) est la fonction de valuation des arcs Graphiquement, par convention, les arcs de valuation nulle ne sont pas représentés; les valuations égales à 1 sont omises (valeur par défaut); dans les autres cas, les valuations sont explicites.
 Place d’entrée et place de sortie • Une place p est une place d’entrée d’une transition t si (p, t) appartient à W. – l’ensemble t = {(p, t, ? ) de W} définit les places d’entrée de t • Une place p est une place de sortie d’une transition t si (t, p, ? ) appartient à W – L’ensemble t = {(t, p, ? ) de W} définit les places de sortie de t
Place d’entrée et place de sortie • Une place p est une place d’entrée d’une transition t si (p, t) appartient à W. – l’ensemble t = {(p, t, ? ) de W} définit les places d’entrée de t • Une place p est une place de sortie d’une transition t si (t, p, ? ) appartient à W – L’ensemble t = {(t, p, ? ) de W} définit les places de sortie de t
 Marquage, transition tirable, franchissement d’une transition On appelle marquage d’un Rd. P (P, T, W) toute fonction m : P N (entiers naturels). Dans un Rd. P (P, T, W), une transition t est tirable dans un marquage M si et seulement si, pour toute place p de t, m(p) > w(p, t) Le franchissement d’un transition t conduit à un nouveau marquage tel que : m’(p) = m(p) – w(p, t) + w(t, p)
Marquage, transition tirable, franchissement d’une transition On appelle marquage d’un Rd. P (P, T, W) toute fonction m : P N (entiers naturels). Dans un Rd. P (P, T, W), une transition t est tirable dans un marquage M si et seulement si, pour toute place p de t, m(p) > w(p, t) Le franchissement d’un transition t conduit à un nouveau marquage tel que : m’(p) = m(p) – w(p, t) + w(t, p)
 Atteignabilité… • Un état Mn est atteignable à partir d’un marquage M 1 (noté M 1 -*-> Mn) si et seulement si il existe une séquence s telle que M 1 -*-> Ms
Atteignabilité… • Un état Mn est atteignable à partir d’un marquage M 1 (noté M 1 -*-> Mn) si et seulement si il existe une séquence s telle que M 1 -*-> Ms
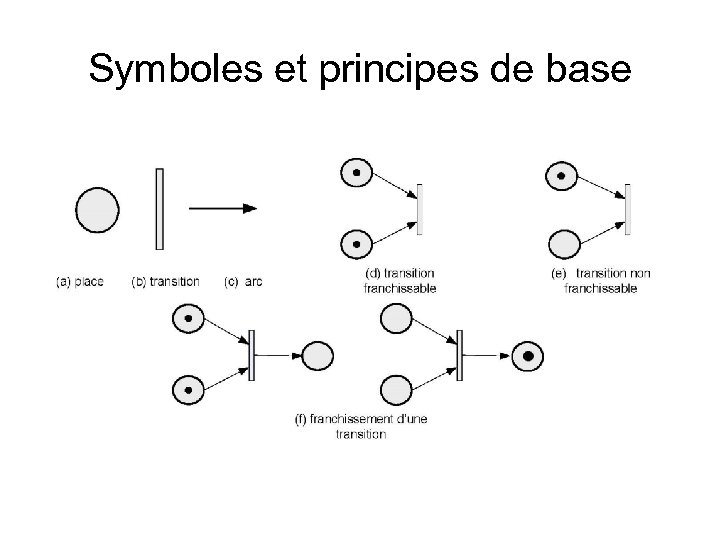 Symboles et principes de base
Symboles et principes de base
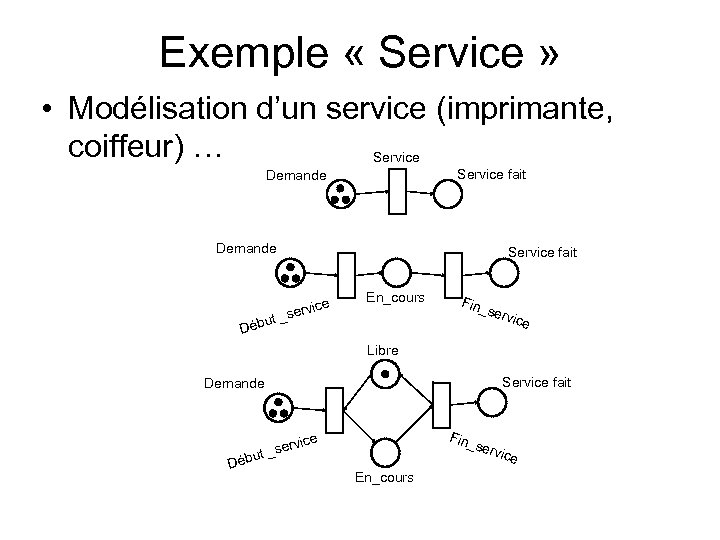 Exemple « Service » • Modélisation d’un service (imprimante, coiffeur) … Service fait Demande Service fait vice _ser En_cours ut Déb Fin_ s ervi ce Libre Service fait Demande Fin_ s ice Déb erv ut _s ervi En_cours ce
Exemple « Service » • Modélisation d’un service (imprimante, coiffeur) … Service fait Demande Service fait vice _ser En_cours ut Déb Fin_ s ervi ce Libre Service fait Demande Fin_ s ice Déb erv ut _s ervi En_cours ce
 Exemple « Service » (P, T, W) • P = {Demande, Libre, En_cours, Service fait} • T = {Début_service, Fin _service} • W = {{Demande, Début_service, 1}, {Libre, Début_service, 1}, {Début_service, En_cours, 1}, {En_cours, Fin_service, 1}, {Fin_service, Libre, 1}, {Fin_service, Services fait, 1}}
Exemple « Service » (P, T, W) • P = {Demande, Libre, En_cours, Service fait} • T = {Début_service, Fin _service} • W = {{Demande, Début_service, 1}, {Libre, Début_service, 1}, {Début_service, En_cours, 1}, {En_cours, Fin_service, 1}, {Fin_service, Libre, 1}, {Fin_service, Services fait, 1}}
 Exemple « Service » ( t, t ) – Début_service = {Demande, Libre} – Fin _service = { En_cours} – Début_service = {En_cours} – Fin_service = {Service fait, Libre}
Exemple « Service » ( t, t ) – Début_service = {Demande, Libre} – Fin _service = { En_cours} – Début_service = {En_cours} – Fin_service = {Service fait, Libre}
 Exemple « Service » (Marquage) • Marquage initial : {m(Demande) =3, m(Libre) =1, m(En_cours) = 0, M(Service fait) = 0} • 1 er pas : – m’(Demande) = m(Demande) – w(Demande, Début_service) + w(Début_service, Demande) = 3 -1 + 0 = 2 – m’(Libre) = m(Libre) – w(Libre, Début_service) + w(Début_service, Libre) = 1 -1 + 0 = 0 – m’(En_cours) = m(En_cours) – w(En_cours, Début_service) + w(Début_service , En_cours) = 0 -0 + 1 = 1
Exemple « Service » (Marquage) • Marquage initial : {m(Demande) =3, m(Libre) =1, m(En_cours) = 0, M(Service fait) = 0} • 1 er pas : – m’(Demande) = m(Demande) – w(Demande, Début_service) + w(Début_service, Demande) = 3 -1 + 0 = 2 – m’(Libre) = m(Libre) – w(Libre, Début_service) + w(Début_service, Libre) = 1 -1 + 0 = 0 – m’(En_cours) = m(En_cours) – w(En_cours, Début_service) + w(Début_service , En_cours) = 0 -0 + 1 = 1
 Propriétés souhaitées/ables des Rd. P • • Vivacité Terminaison Borné A choix libre Bien formé Sans blocage (sans deadlock) Sain
Propriétés souhaitées/ables des Rd. P • • Vivacité Terminaison Borné A choix libre Bien formé Sans blocage (sans deadlock) Sain
 Vérification de ces propriétés • Il existe un lien direct entre ces propriétés des réseaux de Petri et la qualité du processus modélisé • Voir « Chapitre 4 : analyse qualitative des processus »
Vérification de ces propriétés • Il existe un lien direct entre ces propriétés des réseaux de Petri et la qualité du processus modélisé • Voir « Chapitre 4 : analyse qualitative des processus »
 En pratique Modéliser des processus avec des réseaux de Petri.
En pratique Modéliser des processus avec des réseaux de Petri.
 Un processus comme un Worflow-Net • Un Rd. P est un WF-Net ssi : – Une seule place d’entrée et une seule place de sortie – Chaque place et chaque transition se trouve sur un chemin allant de la place initiale à la place finale – La consommation d’un jeton dans la place initiale produit un et un seul jeton dans la place finale
Un processus comme un Worflow-Net • Un Rd. P est un WF-Net ssi : – Une seule place d’entrée et une seule place de sortie – Chaque place et chaque transition se trouve sur un chemin allant de la place initiale à la place finale – La consommation d’un jeton dans la place initiale produit un et un seul jeton dans la place finale
 Exemple
Exemple
 Rd. P Modélisation du flot de contrôle
Rd. P Modélisation du flot de contrôle
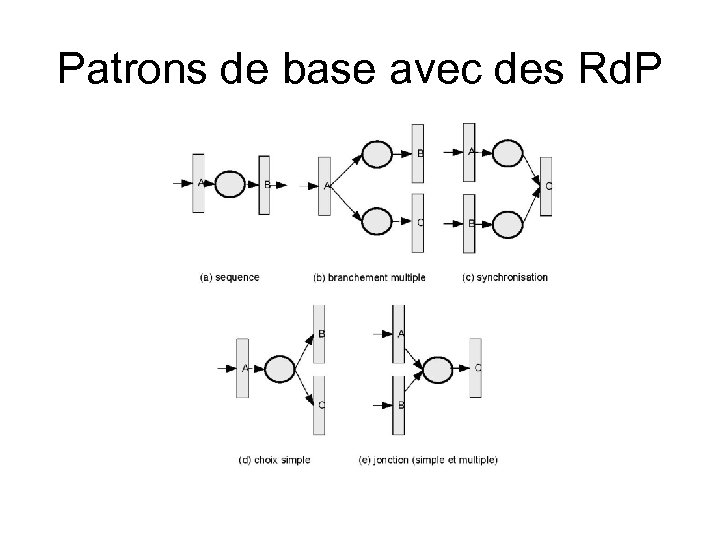 Patrons de base avec des Rd. P
Patrons de base avec des Rd. P
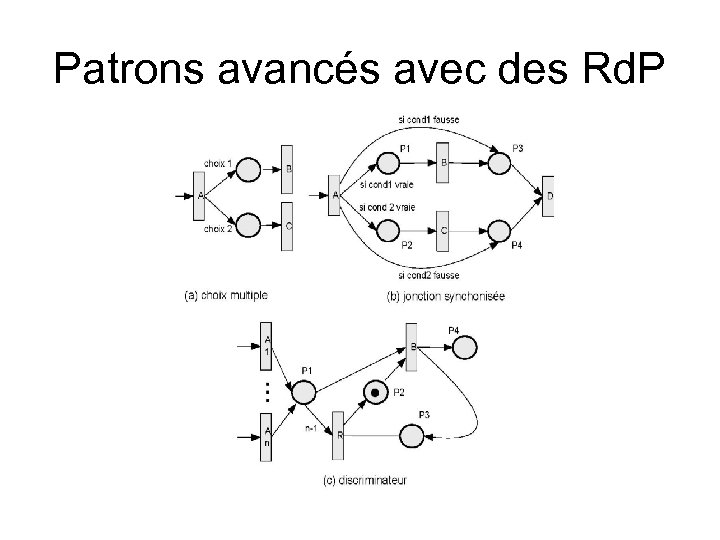 Patrons avancés avec des Rd. P
Patrons avancés avec des Rd. P
 Rd. P Modélisation du flot de données
Rd. P Modélisation du flot de données
 Représentation du flot de données • Le flot de données est porté par (voir Rd. P coloré) : – les couleurs associées aux jetons – le flot des jetons dans le Rd. P et les conditions associées aux transitions • Remarquons que plus les jetons portent d’information, et plus les Rd. P ont tendance à perdre leur lisibilité (graphique)
Représentation du flot de données • Le flot de données est porté par (voir Rd. P coloré) : – les couleurs associées aux jetons – le flot des jetons dans le Rd. P et les conditions associées aux transitions • Remarquons que plus les jetons portent d’information, et plus les Rd. P ont tendance à perdre leur lisibilité (graphique)
 Rd. P Modélisation des ressources
Rd. P Modélisation des ressources
 Les rôles comme des places, les ressources comme des jetons • On ajoute des places spécifiques pour définir les rôles • Les ressources sont les jetons dans ces places spécifiques • Les transitions qui représentent les activités consomment ces ressources • On peut associer des places/ressources à plusieurs transitions • L’ajout de ces places complexifie le Rd. P qui devient moins lisible et plus difficile à valider
Les rôles comme des places, les ressources comme des jetons • On ajoute des places spécifiques pour définir les rôles • Les ressources sont les jetons dans ces places spécifiques • Les transitions qui représentent les activités consomment ces ressources • On peut associer des places/ressources à plusieurs transitions • L’ajout de ces places complexifie le Rd. P qui devient moins lisible et plus difficile à valider
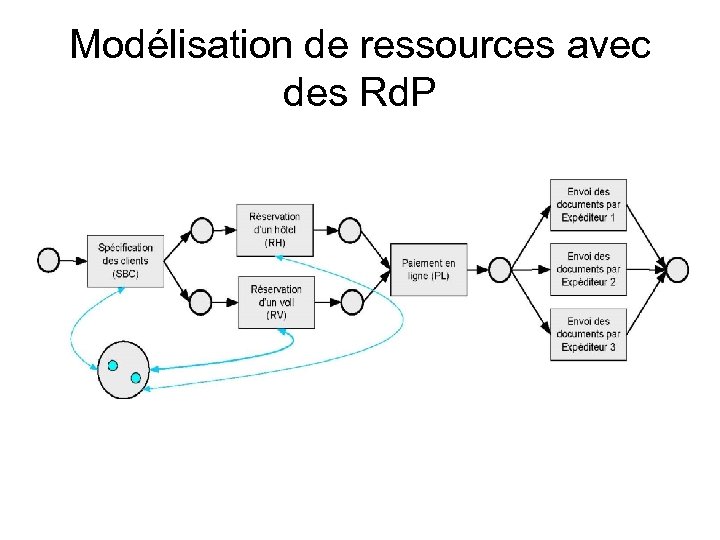 Modélisation de ressources avec des Rd. P
Modélisation de ressources avec des Rd. P
 Limites des Rd. P classiques • Passage à l’échelle • Pouvoir d’expression limité • Pas de modélisation du temps Rd. P hierarchisés Rd. P colorés Rd. P temporisés
Limites des Rd. P classiques • Passage à l’échelle • Pouvoir d’expression limité • Pas de modélisation du temps Rd. P hierarchisés Rd. P colorés Rd. P temporisés
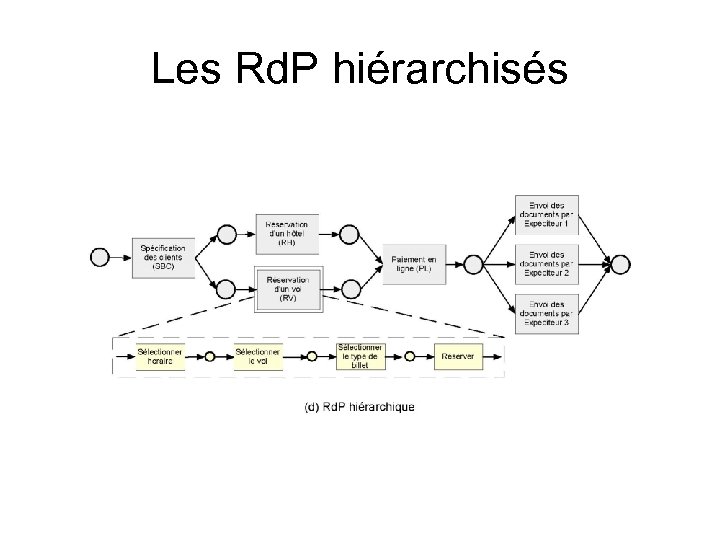 Les Rd. P hiérarchisés
Les Rd. P hiérarchisés
 … permettent de • Plier/déplier un modèle • De représenter le raffinement d’une activité composée en sous-activité
… permettent de • Plier/déplier un modèle • De représenter le raffinement d’une activité composée en sous-activité
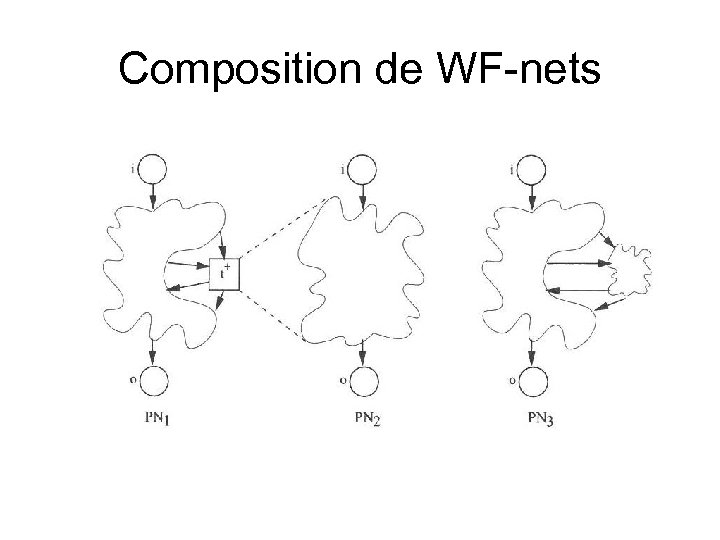 Composition de WF-nets
Composition de WF-nets
 Raffinement d’une transition • PN 3 obtenu par raffinement de t+ de PN 1 par PN 2 : – PN 1 = (P 1, T 1, F 1) et PN 2 = (P 2, T 2, F 2) – T 1 inter T 2 = vide, P 1 inter P 2 = {i, o}, t+ E T 1 – PN 3 = (P 3, T 3, F 3) avec P 3 = P 1 u P 2 , T 3 = (T 1 {t+}) U T 2 – F 3 = {(x, y) E F 1 | x != t+ et y != t+ } U {(x, y) E F 2 | x != i et y != o } U {(x, y) E P 1 x T 2 | {(x, t+) E F 1 et (i, y) E F 2 } U {(x, y) E T 2 x P 1 | {(t+, y) E F 1 et (x, o) E F 2 } (F est la fonction W sans « valuation » : tous les arc ont la valeur « 1 » )
Raffinement d’une transition • PN 3 obtenu par raffinement de t+ de PN 1 par PN 2 : – PN 1 = (P 1, T 1, F 1) et PN 2 = (P 2, T 2, F 2) – T 1 inter T 2 = vide, P 1 inter P 2 = {i, o}, t+ E T 1 – PN 3 = (P 3, T 3, F 3) avec P 3 = P 1 u P 2 , T 3 = (T 1 {t+}) U T 2 – F 3 = {(x, y) E F 1 | x != t+ et y != t+ } U {(x, y) E F 2 | x != i et y != o } U {(x, y) E P 1 x T 2 | {(x, t+) E F 1 et (i, y) E F 2 } U {(x, y) E T 2 x P 1 | {(t+, y) E F 1 et (x, o) E F 2 } (F est la fonction W sans « valuation » : tous les arc ont la valeur « 1 » )
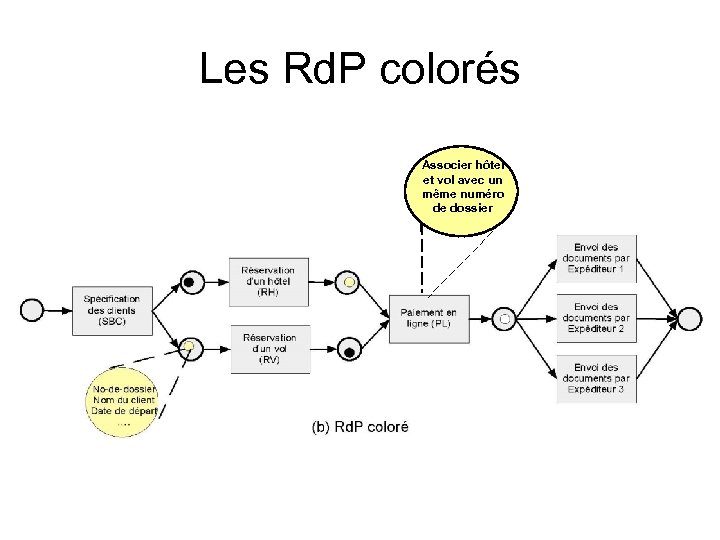 Les Rd. P colorés Associer hôtel et vol avec un même numéro de dossier
Les Rd. P colorés Associer hôtel et vol avec un même numéro de dossier
 … permettent de • De qualifier les jetons avec des attributs • De distinguer les cas • Sur lesquelles peuvent porter des conditions de franchissement
… permettent de • De qualifier les jetons avec des attributs • De distinguer les cas • Sur lesquelles peuvent porter des conditions de franchissement
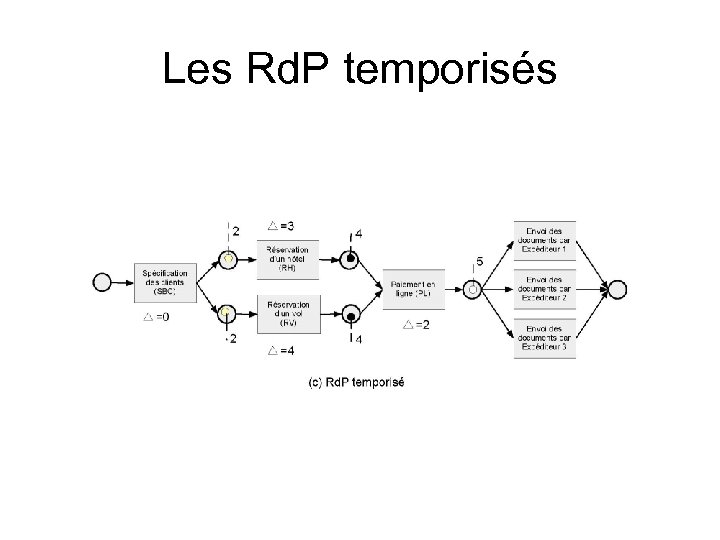 Les Rd. P temporisés
Les Rd. P temporisés
 … permettent de • D’associer des timestamps aux jetons (date à partir de laquelle un jeton peut être consommé) • D’associer des temps de franchissement aux transitions (d’exécution aux activités) • D’ajouter des délais aux activités • Pour faire de la simulation temporelle
… permettent de • D’associer des timestamps aux jetons (date à partir de laquelle un jeton peut être consommé) • D’associer des temps de franchissement aux transitions (d’exécution aux activités) • D’ajouter des délais aux activités • Pour faire de la simulation temporelle
 Conclusion Rd. P • Certainement le fondement principal pour la gestion des flots de contrôle • Quelques outils utiles, mais la validation automatique est loin d’être atteinte • … en particulier pour les réseaux colorés • Les Rd. P sont souvent embarqués de façon cachée dans bons nombres d’outils associés aux SGWf.
Conclusion Rd. P • Certainement le fondement principal pour la gestion des flots de contrôle • Quelques outils utiles, mais la validation automatique est loin d’être atteinte • … en particulier pour les réseaux colorés • Les Rd. P sont souvent embarqués de façon cachée dans bons nombres d’outils associés aux SGWf.
 Exemple (1) Une compagnie d’assurance souhaite modéliser le processus défini comme suit : A l’arrivée d’une déclaration de sinistre, elle fait en parallèle deux vérifications dans deux départements différents : la police d’assurance couvre–t-elle le sinistre ? La déclaration permet-elle de décider du remboursement ? Si la police d’assurance couvre le sinistre (police acceptée) et que la déclaration est acceptée, l’assurance paye. Dans le cas où soit la police d’assurance n’est pas valide, soit la déclaration n’est pas acceptée, un courrier est envoyé à l’adhérent.
Exemple (1) Une compagnie d’assurance souhaite modéliser le processus défini comme suit : A l’arrivée d’une déclaration de sinistre, elle fait en parallèle deux vérifications dans deux départements différents : la police d’assurance couvre–t-elle le sinistre ? La déclaration permet-elle de décider du remboursement ? Si la police d’assurance couvre le sinistre (police acceptée) et que la déclaration est acceptée, l’assurance paye. Dans le cas où soit la police d’assurance n’est pas valide, soit la déclaration n’est pas acceptée, un courrier est envoyé à l’adhérent.
 Exemple (2) En donner un modèle BPMN!
Exemple (2) En donner un modèle BPMN!
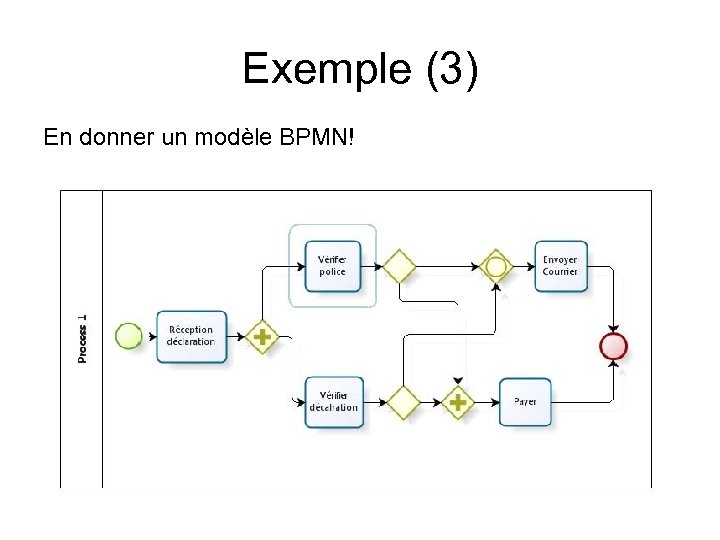 Exemple (3) En donner un modèle BPMN!
Exemple (3) En donner un modèle BPMN!
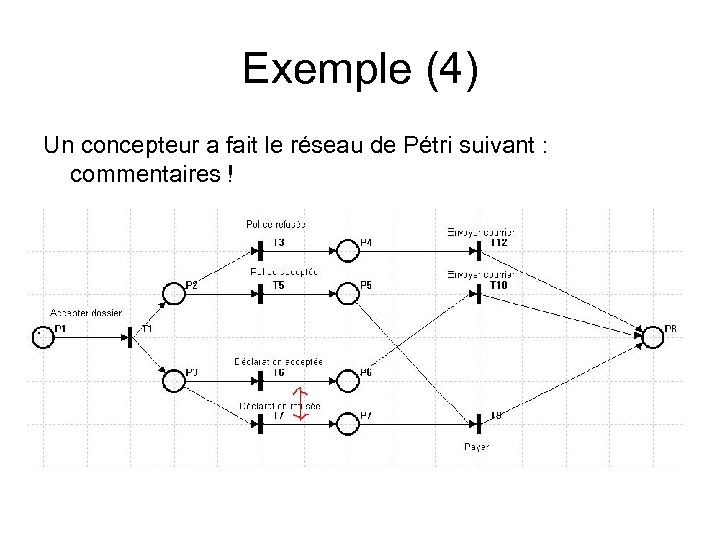 Exemple (4) Un concepteur a fait le réseau de Pétri suivant : commentaires !
Exemple (4) Un concepteur a fait le réseau de Pétri suivant : commentaires !
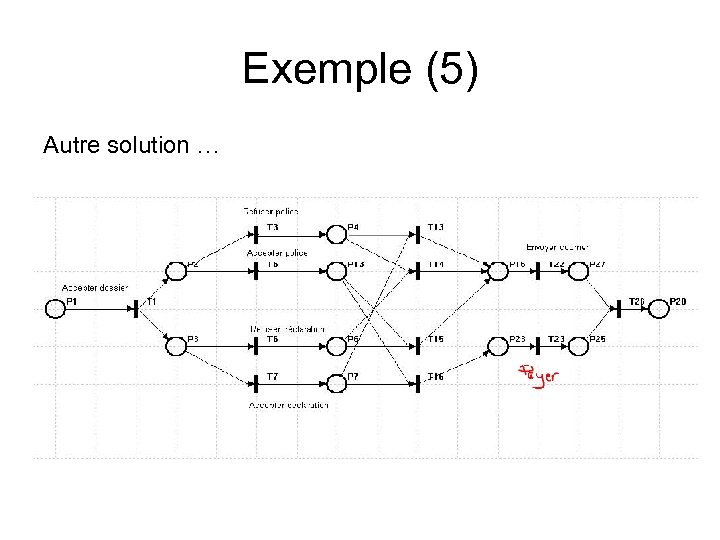 Exemple (5) Autre solution …
Exemple (5) Autre solution …
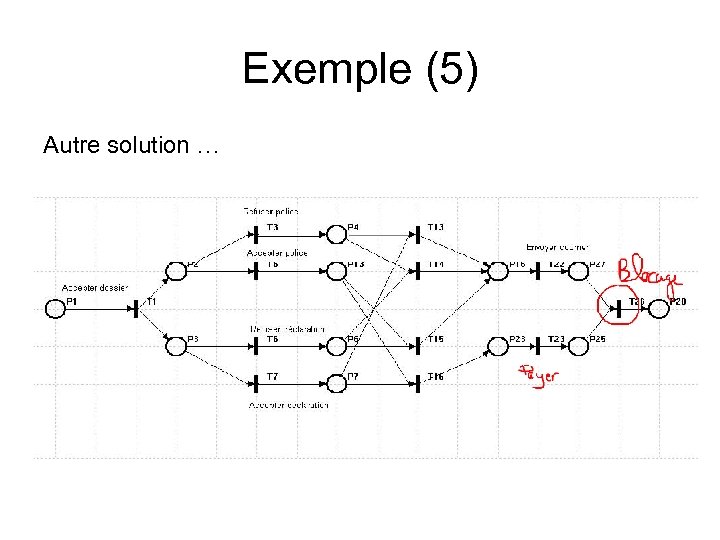 Exemple (5) Autre solution …
Exemple (5) Autre solution …
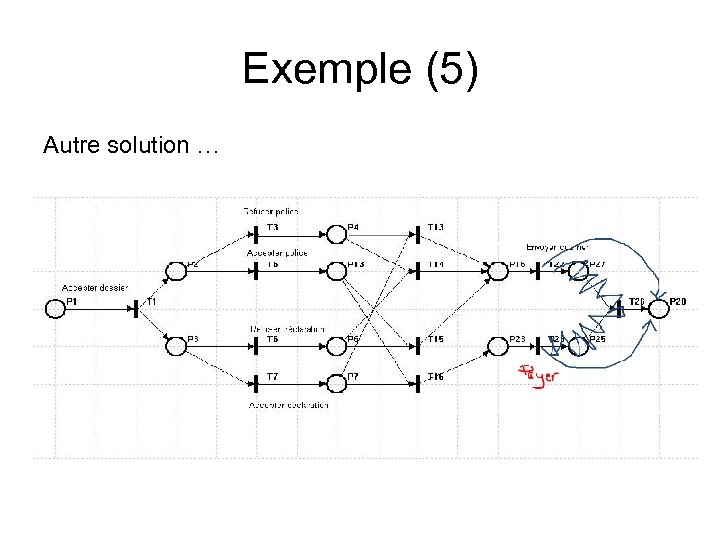 Exemple (5) Autre solution …
Exemple (5) Autre solution …
 Conclusion (1) • Le chapitre présente plus des notations formelles qu’une méthodologie d’analyse/conception comme introduite dans • Cependant, le fait de modéliser en se demandant si le processus est bien structuré, bien parenthèse, à choix libre …supporte une discipline de conception efficace
Conclusion (1) • Le chapitre présente plus des notations formelles qu’une méthodologie d’analyse/conception comme introduite dans • Cependant, le fait de modéliser en se demandant si le processus est bien structuré, bien parenthèse, à choix libre …supporte une discipline de conception efficace
 Conclusion (2) • Rd. P est probablement le modèle formel le mieux outillé • UML est utilisé en phase d’analyse et de conception lorsque le processus est embarqué dans un contexte logiciel plus large • EPC est très utilisé en pratique dans le contexte ERP, mais les outils EPC « emballent » les concepts des Rd. P
Conclusion (2) • Rd. P est probablement le modèle formel le mieux outillé • UML est utilisé en phase d’analyse et de conception lorsque le processus est embarqué dans un contexte logiciel plus large • EPC est très utilisé en pratique dans le contexte ERP, mais les outils EPC « emballent » les concepts des Rd. P
![Références • • • • [AAL 00] VAN DER AALST W. M. P. , Références • • • • [AAL 00] VAN DER AALST W. M. P. ,](https://present5.com/presentation/45c8008e54e2a18bf51995e2a03ae988/image-101.jpg) Références • • • • [AAL 00] VAN DER AALST W. M. P. , TER HOFSTEDE A. H. M. , « Verification of Workflow Task Structures : A Petri-net-baset Approach » , Inf. Syst. , vol. 25, n˚ 1, p. 43 -69, 2000. [AAL 02] VAN DER AALST W. M. P. , VAN HEE K. M. , Workflow Management : Models, Methods, and Systems, MIT Press, Cambridge, 2002. [AAL 11] VAN DER AALST W. M. P. , STAHL C. Modelling Business Processes : A Petri Net. Oriented Aproach, MIT Press, Cambridge, 2011. [DON 05] VAN DONGEN B. F. , VAN DER AALST W. M. P. , VERBEEK H. M. W. , « Verification of EPCs : Using Reduction Rules and Petri Nets » , CAi. SE, p. 372 -386, 2005. [DUM 12 a] DUMAS M. and al. Understanding Business Process Models: The Costs and Benefits of Structuredness, CAISE 2012 [DUM 90 a] DUMAS P. , CHARBONNEL G. , La méthode OSSAD : pour maîtriser les technologies de l’information - Tome I : Principes, Editions d’Organisation, Paris, 1990. [DUM 90 b] DUMAS P. , CHARBONNEL G. , La méthode OSSAD : pour maîtriser les technologies de l’information - Tome II : Guide pratique, Editions d’Organisation, Paris, 1990. [EPC 08] EPC, « Event-driven Process Chain » , en. wikipedia. org/wiki/Event-driven_Process- Chains, 2008. [FAW 97] FAWLER M. , Uml distilled. Applying the standard object modeling language, Addison. Wesley, Reading, 1997. [FAW 05] FAWLER M. , Uml distilled. A brief guide to the standard object modeling language, Addison-Wesley, Reading, 2005. [FOS 05] FOSTER H. , UCHITEL S. , MAGEE J. , KRAMER J. , HU M. , « Using a Rigorous Approach for Engineering Web Service Compositions : A Case Study » , IEEE Service Computing Conference, p. 217 -224, 2005. [FU 04] FU X. , BULTAN T. , SU J. , « Analysis of interacting BPEL web services » , Wold Wide Web conference, p. 621 -630, 2004. [GEF 08] GEFFROY J. C. , Introduction aux réseaux de Petri, cyranac. free. fr/pub/cours/cnam. MOCA/CH 10. pdf, 2008.
Références • • • • [AAL 00] VAN DER AALST W. M. P. , TER HOFSTEDE A. H. M. , « Verification of Workflow Task Structures : A Petri-net-baset Approach » , Inf. Syst. , vol. 25, n˚ 1, p. 43 -69, 2000. [AAL 02] VAN DER AALST W. M. P. , VAN HEE K. M. , Workflow Management : Models, Methods, and Systems, MIT Press, Cambridge, 2002. [AAL 11] VAN DER AALST W. M. P. , STAHL C. Modelling Business Processes : A Petri Net. Oriented Aproach, MIT Press, Cambridge, 2011. [DON 05] VAN DONGEN B. F. , VAN DER AALST W. M. P. , VERBEEK H. M. W. , « Verification of EPCs : Using Reduction Rules and Petri Nets » , CAi. SE, p. 372 -386, 2005. [DUM 12 a] DUMAS M. and al. Understanding Business Process Models: The Costs and Benefits of Structuredness, CAISE 2012 [DUM 90 a] DUMAS P. , CHARBONNEL G. , La méthode OSSAD : pour maîtriser les technologies de l’information - Tome I : Principes, Editions d’Organisation, Paris, 1990. [DUM 90 b] DUMAS P. , CHARBONNEL G. , La méthode OSSAD : pour maîtriser les technologies de l’information - Tome II : Guide pratique, Editions d’Organisation, Paris, 1990. [EPC 08] EPC, « Event-driven Process Chain » , en. wikipedia. org/wiki/Event-driven_Process- Chains, 2008. [FAW 97] FAWLER M. , Uml distilled. Applying the standard object modeling language, Addison. Wesley, Reading, 1997. [FAW 05] FAWLER M. , Uml distilled. A brief guide to the standard object modeling language, Addison-Wesley, Reading, 2005. [FOS 05] FOSTER H. , UCHITEL S. , MAGEE J. , KRAMER J. , HU M. , « Using a Rigorous Approach for Engineering Web Service Compositions : A Case Study » , IEEE Service Computing Conference, p. 217 -224, 2005. [FU 04] FU X. , BULTAN T. , SU J. , « Analysis of interacting BPEL web services » , Wold Wide Web conference, p. 621 -630, 2004. [GEF 08] GEFFROY J. C. , Introduction aux réseaux de Petri, cyranac. free. fr/pub/cours/cnam. MOCA/CH 10. pdf, 2008.
![Références • • • • [LIA 07] LIANG-JIE ZHANG JIA ZHANG H. C. , Références • • • • [LIA 07] LIANG-JIE ZHANG JIA ZHANG H. C. ,](https://present5.com/presentation/45c8008e54e2a18bf51995e2a03ae988/image-102.jpg) Références • • • • [LIA 07] LIANG-JIE ZHANG JIA ZHANG H. C. , Services Computing, Springer, Berlin, 2007. [MAR 95] MARSAN M. A. , BALBO G. , DONATELLI S. , FRANCESCHINIS G. , Modelling with Generalized Stochastic Petri Nets, Springer-Verlag, Heidelberg, 1995. [OBE 96] OBERWEIS A. , SANDER P. , « Information system behavior specification by high level Petri nets » , ACM Transactions on Information Systems, vol. 14, n˚ 4, p. 380 -420, ACM, 1996. [OMG 06] OMG, « Business Process Definition Metamodel » , www. omg. org/docs/bei/03 -0106. pdf, 2006. [PAP 07] PAPAZOGLOU M. P. , VAN DEN HEUVEL W. J. , « Business process development life cycle methodology » , Communication of ACM, vol. 50, n˚ 10, p. 79 -85, 2007. [PET 08] PETRI, « Réseaux de Petri » , fr. wikipedia. org/wiki/R%C 3%A 9 seau_de_Petri, 2008. [RUM 00] RUMBAUGH J. , BOOCH G. , JACOBSON I. , Le guide de l’utilisateur UML, Eyrolles, Paris, 2000. [SAD 00] SADIQ W. , ORLOWSKA M. E. , « Analysing Process Models Using Graph Reduction. Techniques » , Information Systems, vol. 25 -2, p. 117 -134, 2000. [SAL 04] SALAÜN G. , BORDEAUX L. , SCHAERF M. , « Describing and Reasoning on Web Services using Process Algebra » , International conference on Web Services, 2004. [SAP 08 a] SAP, « SAP Net. Weaver » , en. wikipedia. org/wiki/Net. Weaver, 2008. [SAP 08 b] SAP, « SAP R/3 » , en. wikipedia. org/wiki/SAP_R/3, 2008. [SCH 98] SCHEER A. W. , Business Process Engineering : Reference Models for Industrial Enterprises, Springer-Verlag, Heidelberg, 1998. [TUR 07] TURNER K. J. , « Representing and analysing composed web services using Cress » , J. Network and Computer Applications, vol. 30, n˚ 2, p. 541 -562, 2007
Références • • • • [LIA 07] LIANG-JIE ZHANG JIA ZHANG H. C. , Services Computing, Springer, Berlin, 2007. [MAR 95] MARSAN M. A. , BALBO G. , DONATELLI S. , FRANCESCHINIS G. , Modelling with Generalized Stochastic Petri Nets, Springer-Verlag, Heidelberg, 1995. [OBE 96] OBERWEIS A. , SANDER P. , « Information system behavior specification by high level Petri nets » , ACM Transactions on Information Systems, vol. 14, n˚ 4, p. 380 -420, ACM, 1996. [OMG 06] OMG, « Business Process Definition Metamodel » , www. omg. org/docs/bei/03 -0106. pdf, 2006. [PAP 07] PAPAZOGLOU M. P. , VAN DEN HEUVEL W. J. , « Business process development life cycle methodology » , Communication of ACM, vol. 50, n˚ 10, p. 79 -85, 2007. [PET 08] PETRI, « Réseaux de Petri » , fr. wikipedia. org/wiki/R%C 3%A 9 seau_de_Petri, 2008. [RUM 00] RUMBAUGH J. , BOOCH G. , JACOBSON I. , Le guide de l’utilisateur UML, Eyrolles, Paris, 2000. [SAD 00] SADIQ W. , ORLOWSKA M. E. , « Analysing Process Models Using Graph Reduction. Techniques » , Information Systems, vol. 25 -2, p. 117 -134, 2000. [SAL 04] SALAÜN G. , BORDEAUX L. , SCHAERF M. , « Describing and Reasoning on Web Services using Process Algebra » , International conference on Web Services, 2004. [SAP 08 a] SAP, « SAP Net. Weaver » , en. wikipedia. org/wiki/Net. Weaver, 2008. [SAP 08 b] SAP, « SAP R/3 » , en. wikipedia. org/wiki/SAP_R/3, 2008. [SCH 98] SCHEER A. W. , Business Process Engineering : Reference Models for Industrial Enterprises, Springer-Verlag, Heidelberg, 1998. [TUR 07] TURNER K. J. , « Representing and analysing composed web services using Cress » , J. Network and Computer Applications, vol. 30, n˚ 2, p. 541 -562, 2007
 Fin
Fin
 Rd. P réversible • Un marquage a la propriété home-marking s’il peut toujours être à nouveau atteint • Un Rd. P est réversible si son état initial est un home-marking
Rd. P réversible • Un marquage a la propriété home-marking s’il peut toujours être à nouveau atteint • Un Rd. P est réversible si son état initial est un home-marking
 Rd. P Principes de modélisation
Rd. P Principes de modélisation
 WF-net * • Soit un WF-net WFN, on note WFN* WFN étendu par une transition de la place de sortie o à la place d’entrée i
WF-net * • Soit un WF-net WFN, on note WFN* WFN étendu par une transition de la place de sortie o à la place d’entrée i
 Rd. P vivace • Une transition est morte si et seulement si elle n’est pas tirée dans aucun marquage possible • Une transition est vivante si, depuis n’importe quel marquage, on peut atteindre un marquage dans lequel la transition est tirable • Un Rd. P est vivace si et seulement si toutes ses transitions sont vivantes • Vivacité et terminaison s’excluent.
Rd. P vivace • Une transition est morte si et seulement si elle n’est pas tirée dans aucun marquage possible • Une transition est vivante si, depuis n’importe quel marquage, on peut atteindre un marquage dans lequel la transition est tirable • Un Rd. P est vivace si et seulement si toutes ses transitions sont vivantes • Vivacité et terminaison s’excluent.
 Rd. P qui termine • Un Rd. P termine s’il atteint toujours un marquage terminal duquel aucune transition ne peut être tirée • Un Rd. P avec graphe d’atteignabilité fini et acyclique termine • Vivacité et terminaison s’excluent.
Rd. P qui termine • Un Rd. P termine s’il atteint toujours un marquage terminal duquel aucune transition ne peut être tirée • Un Rd. P avec graphe d’atteignabilité fini et acyclique termine • Vivacité et terminaison s’excluent.
 Rd. P borné • L’absence d’une borne limite pour le nombre de jetons dans une place est généralement source de problème • Un Rd. P est k-borné (bounded) si, depuis le marquage initial, il ne peut atteindre aucun marquage dans lequel il y a plus de k jetons; dans le cas contraire, il est non borné • Un Rd. P borné a toujours un nombre de marquages fini • SI K=1, le Rd. P est dit sûr (safe). ©Les processus métiers: concepts, modèles et systèmes
Rd. P borné • L’absence d’une borne limite pour le nombre de jetons dans une place est généralement source de problème • Un Rd. P est k-borné (bounded) si, depuis le marquage initial, il ne peut atteindre aucun marquage dans lequel il y a plus de k jetons; dans le cas contraire, il est non borné • Un Rd. P borné a toujours un nombre de marquages fini • SI K=1, le Rd. P est dit sûr (safe). ©Les processus métiers: concepts, modèles et systèmes
 Blocage, Boucle , Borne • Un Rd. P est sans blocage s’il n’y a pas de cas où l’activité finale ne peut pas s’exécuter et où le processus ne peut plus progresser • Un Rd. P est sans boucle si tous les cas terminent • Un Rd. P est borné s’il n’existe pas un cas où le nombre de jeton croit indéfiniment ©Les processus métiers: concepts, modèles et systèmes
Blocage, Boucle , Borne • Un Rd. P est sans blocage s’il n’y a pas de cas où l’activité finale ne peut pas s’exécuter et où le processus ne peut plus progresser • Un Rd. P est sans boucle si tous les cas terminent • Un Rd. P est borné s’il n’existe pas un cas où le nombre de jeton croit indéfiniment ©Les processus métiers: concepts, modèles et systèmes
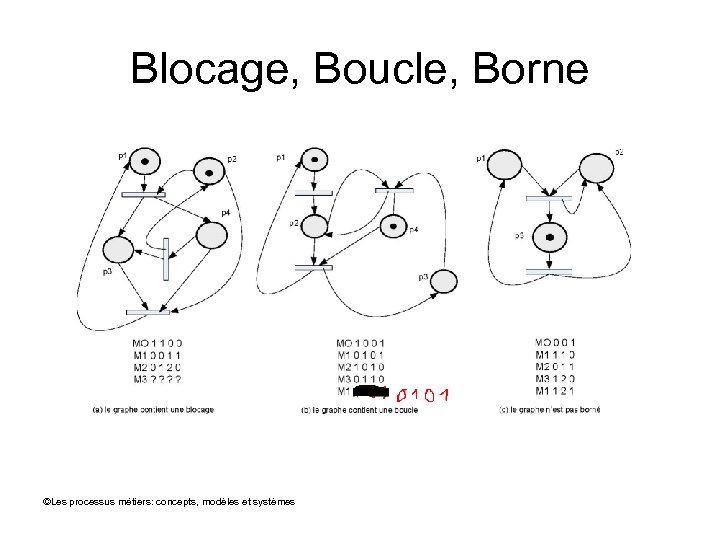 Blocage, Boucle, Borne ©Les processus métiers: concepts, modèles et systèmes
Blocage, Boucle, Borne ©Les processus métiers: concepts, modèles et systèmes
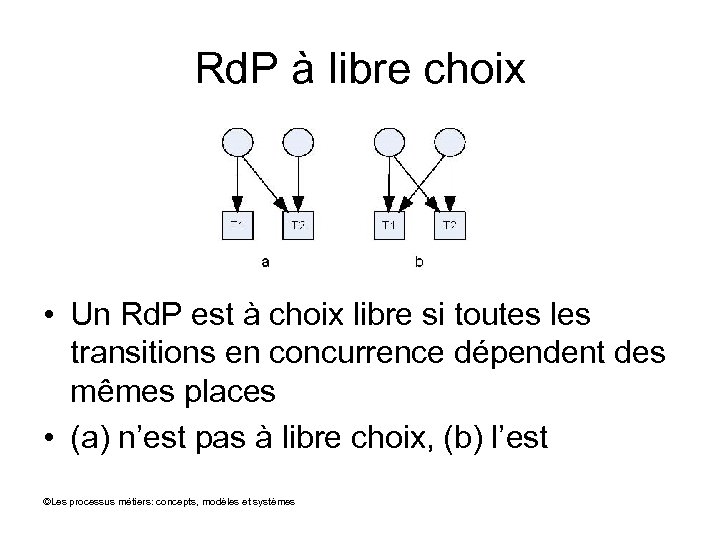 Rd. P à libre choix • Un Rd. P est à choix libre si toutes les transitions en concurrence dépendent des mêmes places • (a) n’est pas à libre choix, (b) l’est ©Les processus métiers: concepts, modèles et systèmes
Rd. P à libre choix • Un Rd. P est à choix libre si toutes les transitions en concurrence dépendent des mêmes places • (a) n’est pas à libre choix, (b) l’est ©Les processus métiers: concepts, modèles et systèmes
 Rd. P bien formé • Un Rd. P PN est bien formé si et seulement il existe un état initial à partir duquel il est vivace et borné ©Les processus métiers: concepts, modèles et systèmes
Rd. P bien formé • Un Rd. P PN est bien formé si et seulement il existe un état initial à partir duquel il est vivace et borné ©Les processus métiers: concepts, modèles et systèmes
 Chemin (élémentaire, sans conflit) • Soit N = P U T l’ensemble des nœuds d’un Rd. P PN, un chemin C d’un nœud n 1 à un nœud nk est une séquence
Chemin (élémentaire, sans conflit) • Soit N = P U T l’ensemble des nœuds d’un Rd. P PN, un chemin C d’un nœud n 1 à un nœud nk est une séquence
 Rd. P fortement connecté • Un Rd. P est fortement connecté ssi, pour chaque paire de nœud x et y, il existe un chemin de x à y ©Les processus métiers: concepts, modèles et systèmes
Rd. P fortement connecté • Un Rd. P est fortement connecté ssi, pour chaque paire de nœud x et y, il existe un chemin de x à y ©Les processus métiers: concepts, modèles et systèmes
 Well handled • Un Rd. P est well handled ssi, pour chaque paire de nœud x et y, où x est une place et l’autre une transition, et pour chaque paire de chemin élémentaire C 1 et C 2 de x à y, alphabet(C 1) inter alphabet(C 2) = {x, y} => C 1 = C 2 ©Les processus métiers: concepts, modèles et systèmes
Well handled • Un Rd. P est well handled ssi, pour chaque paire de nœud x et y, où x est une place et l’autre une transition, et pour chaque paire de chemin élémentaire C 1 et C 2 de x à y, alphabet(C 1) inter alphabet(C 2) = {x, y} => C 1 = C 2 ©Les processus métiers: concepts, modèles et systèmes
 Rd. P sans deadlock • Un Rd. P est sans deadlock si et seulement si au moins une transition peut être tirée dans n’importe quel état ©Les processus métiers: concepts, modèles et systèmes
Rd. P sans deadlock • Un Rd. P est sans deadlock si et seulement si au moins une transition peut être tirée dans n’importe quel état ©Les processus métiers: concepts, modèles et systèmes
 Rd. P Validation ©Les processus métiers: concepts, modèles et systèmes
Rd. P Validation ©Les processus métiers: concepts, modèles et systèmes
 Processus sain • Un processus sain est un processus qui ne contient pas d’activité inutile et où chaque cas se termine complètement sans laisser de référence à lui-même • La vérification brute de cette propriété conduit à une explosion combinatoire • Mais un WF-net, augmenté de o i, qui est vivace et borné est sain • Un WF-net est vivace s’il est sans blocage et sans boucle : on sait vérifier ces propriétés ©Les processus métiers: concepts, modèles et systèmes
Processus sain • Un processus sain est un processus qui ne contient pas d’activité inutile et où chaque cas se termine complètement sans laisser de référence à lui-même • La vérification brute de cette propriété conduit à une explosion combinatoire • Mais un WF-net, augmenté de o i, qui est vivace et borné est sain • Un WF-net est vivace s’il est sans blocage et sans boucle : on sait vérifier ces propriétés ©Les processus métiers: concepts, modèles et systèmes
 WF-net bien structuré • Un wf-net est bien structuré ssi WFN * est « well handled » • Décider si un WF-net bien structuré est sain est calculable en un temps polynomial • Par construction, un Rd. P well handled et fortement connecté est bien formé (vivace et borné), donc sain ©Les processus métiers: concepts, modèles et systèmes
WF-net bien structuré • Un wf-net est bien structuré ssi WFN * est « well handled » • Décider si un WF-net bien structuré est sain est calculable en un temps polynomial • Par construction, un Rd. P well handled et fortement connecté est bien formé (vivace et borné), donc sain ©Les processus métiers: concepts, modèles et systèmes
 Raffinement d’un transition • Propriétés: – Si (PN 1, i) est sûr et PN 1 et PN 2 sont sains, alors PN 3 est sain – (PN 1, i) et (PN 2, i) sont sûrs (resp CL) et sains ssi PN 3 est sûr (resp. CL) et sain – Si PN 3 est à choix libre, resp. bien structuré, alors PN 1 et PN 2 sont à CL, resp. BS – Si PN 3 est bien structuré et sain, alors PN 1 et PN 2 sont bien structurés et sains ©Les processus métiers: concepts, modèles et systèmes
Raffinement d’un transition • Propriétés: – Si (PN 1, i) est sûr et PN 1 et PN 2 sont sains, alors PN 3 est sain – (PN 1, i) et (PN 2, i) sont sûrs (resp CL) et sains ssi PN 3 est sûr (resp. CL) et sain – Si PN 3 est à choix libre, resp. bien structuré, alors PN 1 et PN 2 sont à CL, resp. BS – Si PN 3 est bien structuré et sain, alors PN 1 et PN 2 sont bien structurés et sains ©Les processus métiers: concepts, modèles et systèmes
 En pratique ©Les processus métiers: concepts, modèles et systèmes
En pratique ©Les processus métiers: concepts, modèles et systèmes
 Processus-Rd. P bien structuré • Bonnes pratiques qui éliminent par construction bien des risques • En tous cas, diminue la complexité du réseau • En conséquence l’évaluation est plus efficace ©Les processus métiers: concepts, modèles et systèmes
Processus-Rd. P bien structuré • Bonnes pratiques qui éliminent par construction bien des risques • En tous cas, diminue la complexité du réseau • En conséquence l’évaluation est plus efficace ©Les processus métiers: concepts, modèles et systèmes
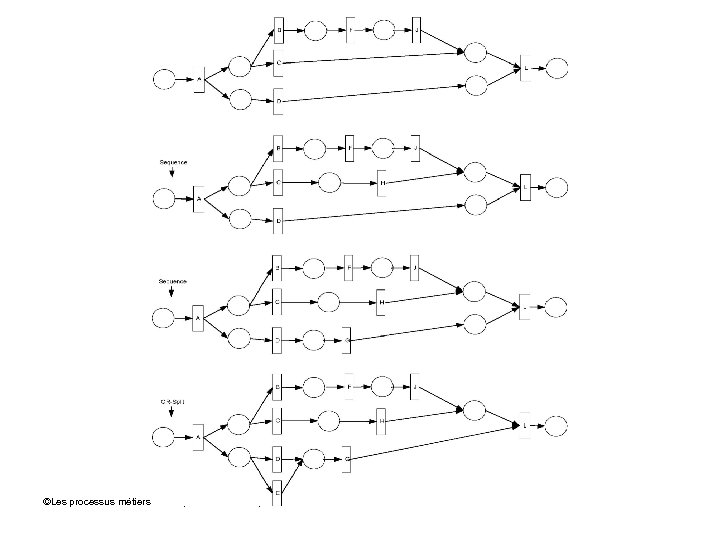
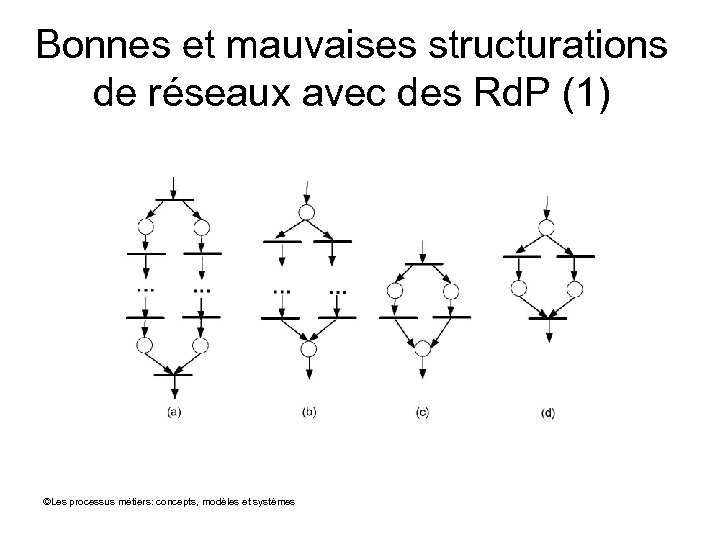 Bonnes et mauvaises structurations de réseaux avec des Rd. P (1) ©Les processus métiers: concepts, modèles et systèmes
Bonnes et mauvaises structurations de réseaux avec des Rd. P (1) ©Les processus métiers: concepts, modèles et systèmes
 Bonnes et mauvaises structurations de réseaux avec des Rd. P (2) • (a) combine un AND_Split et un AND-join, (b) combine un XOR-Split et un XOR-JOIN (a) et (b) sont bien structurés • (c) et (d) sont mal structurés ©Les processus métiers: concepts, modèles et systèmes
Bonnes et mauvaises structurations de réseaux avec des Rd. P (2) • (a) combine un AND_Split et un AND-join, (b) combine un XOR-Split et un XOR-JOIN (a) et (b) sont bien structurés • (c) et (d) sont mal structurés ©Les processus métiers: concepts, modèles et systèmes
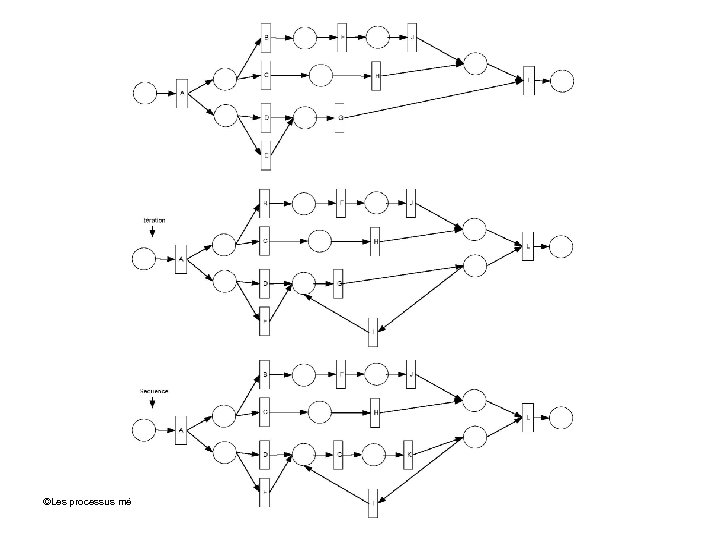
 Well-structured WF-Net Un WF-Net bien structuré est un WF-Net bien parenthésé ©Les processus métiers: concepts, modèles et systèmes
Well-structured WF-Net Un WF-Net bien structuré est un WF-Net bien parenthésé ©Les processus métiers: concepts, modèles et systèmes
 Rd. P sains par construction • On connaît un ensemble de Rd. P de base sains • Leur composition produit un Rd. P sain Application : ayant un Rd. P, peut-on le reconstruire en itérant la composition de Rd. P de base sains ©Les processus métiers: concepts, modèles et systèmes
Rd. P sains par construction • On connaît un ensemble de Rd. P de base sains • Leur composition produit un Rd. P sain Application : ayant un Rd. P, peut-on le reconstruire en itérant la composition de Rd. P de base sains ©Les processus métiers: concepts, modèles et systèmes
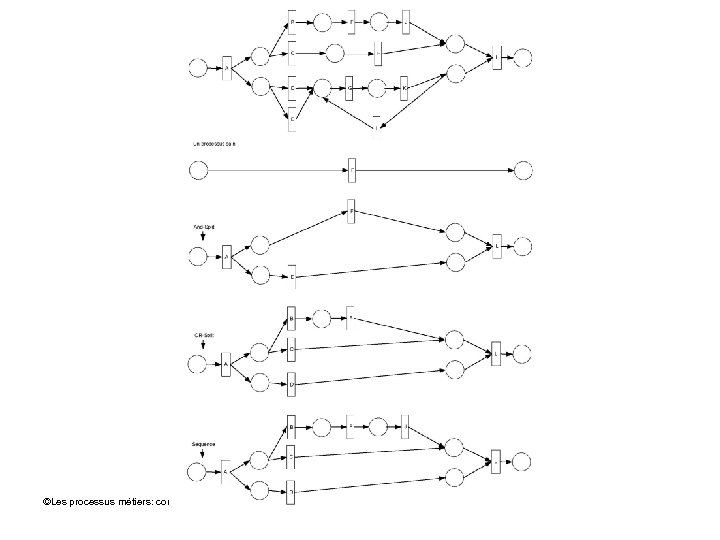
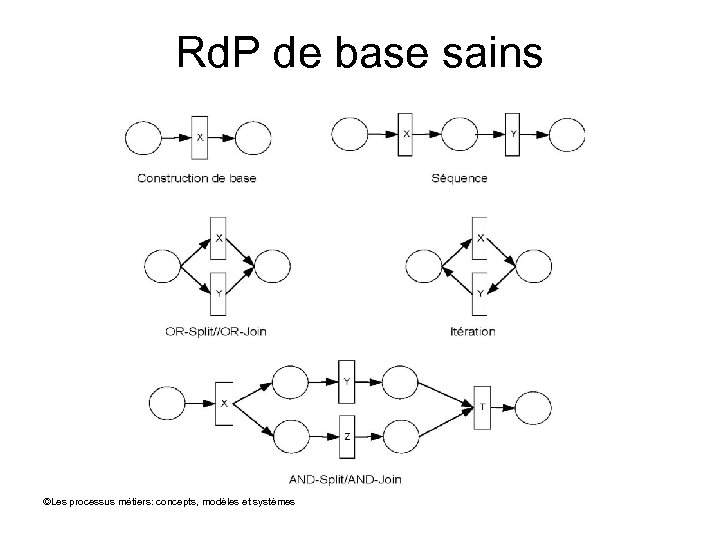 Rd. P de base sains ©Les processus métiers: concepts, modèles et systèmes
Rd. P de base sains ©Les processus métiers: concepts, modèles et systèmes
 ©Les processus métiers: concepts, modèles et systèmes
©Les processus métiers: concepts, modèles et systèmes
 ©Les processus métiers: concepts, modèles et systèmes
©Les processus métiers: concepts, modèles et systèmes
 ©Les processus métiers: concepts, modèles et systèmes
©Les processus métiers: concepts, modèles et systèmes
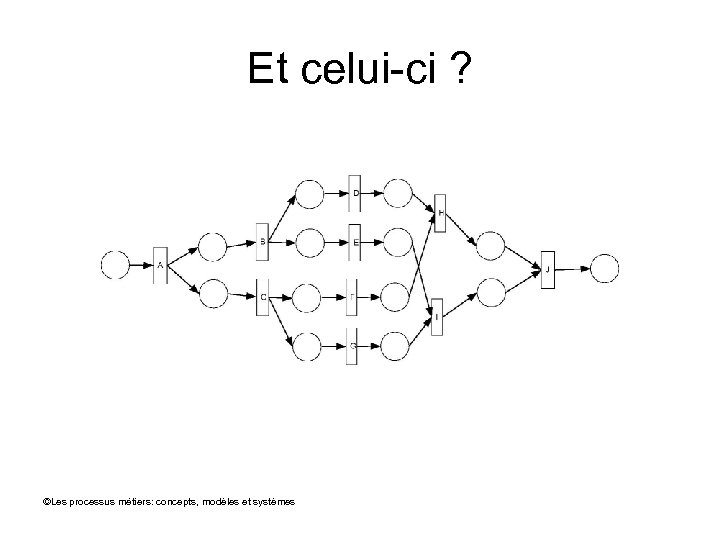 Et celui-ci ? ©Les processus métiers: concepts, modèles et systèmes
Et celui-ci ? ©Les processus métiers: concepts, modèles et systèmes
 Analyse quantitative • Analyse par simulation – évaluation de propriétés recherchées • par visualisation de cas • évaluation de traces d’exécution • Réseaux temporisés pour l’évaluation de performance • Réseaux stochastiques pour l’évaluation de probabilités de franchissement d’une transition … ©Les processus métiers: concepts, modèles et systèmes
Analyse quantitative • Analyse par simulation – évaluation de propriétés recherchées • par visualisation de cas • évaluation de traces d’exécution • Réseaux temporisés pour l’évaluation de performance • Réseaux stochastiques pour l’évaluation de probabilités de franchissement d’une transition … ©Les processus métiers: concepts, modèles et systèmes
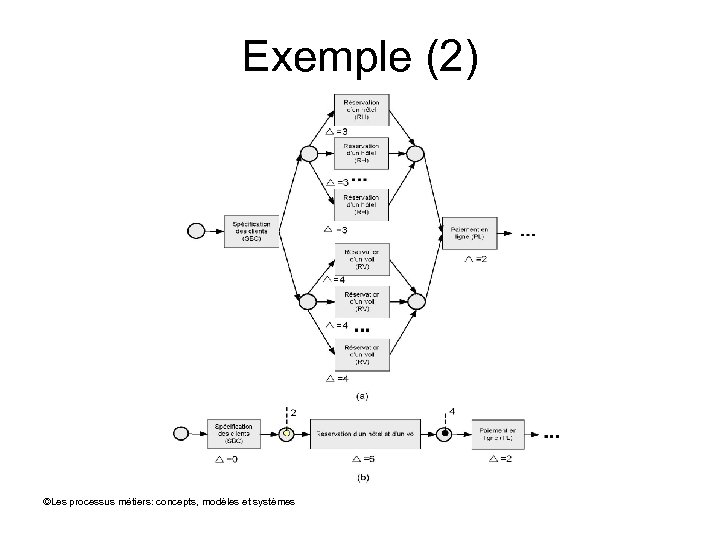 Exemple (2) ©Les processus métiers: concepts, modèles et systèmes
Exemple (2) ©Les processus métiers: concepts, modèles et systèmes
 Exemple (2) • Dans la variante (a), plusieurs activités de réservation d’hôtels et de vols s’exécutent en parallèle, dans la variante (b) une seule activité pour toutes les réservations • L’analyse peut permettre d’évaluer quelle est la stratégie la plus efficace, éventuellement en fonction de circonstances ©Les processus métiers: concepts, modèles et systèmes
Exemple (2) • Dans la variante (a), plusieurs activités de réservation d’hôtels et de vols s’exécutent en parallèle, dans la variante (b) une seule activité pour toutes les réservations • L’analyse peut permettre d’évaluer quelle est la stratégie la plus efficace, éventuellement en fonction de circonstances ©Les processus métiers: concepts, modèles et systèmes


