Les acides et les bases Réactions en solution

Les acides et les bases Réactions en solution aqueuse 1

Plan du cours acides-bases I. III. IV. V. VI. Définition de BRONSTED Réaction des acides et des bases dans l’eau Calcul du p. H de quelques solutions Abondance relative des espèces Dosage d’un acide faible par une base faible Les solutions tampons 2

I. Définition de BRONSTED • Un acide libère H+ AH A- + H+ • Une base fixe H+ B + H+ BH+ • Une réaction acide-base est un échange de H+ AH + B A- + BH+ acide 1 base 2 base 1 acide 2 AH/A- et BH+/B constituent des couples acide/base conjugués 3

Plan du cours acides-base I. II. Définition de BRONSTED Réaction des acides et des bases dans l’eau 4

II. Réaction des acides et des bases dans l’eau i. iii. iv. v. vi. Caractère ampholyte de l’eau Mise en solution d’un acide dans l’eau Mise en solution d’une base dans l’eau Force des espèces conjuguées Effet de nivellement de l’eau Définition de l’opérateur p 5

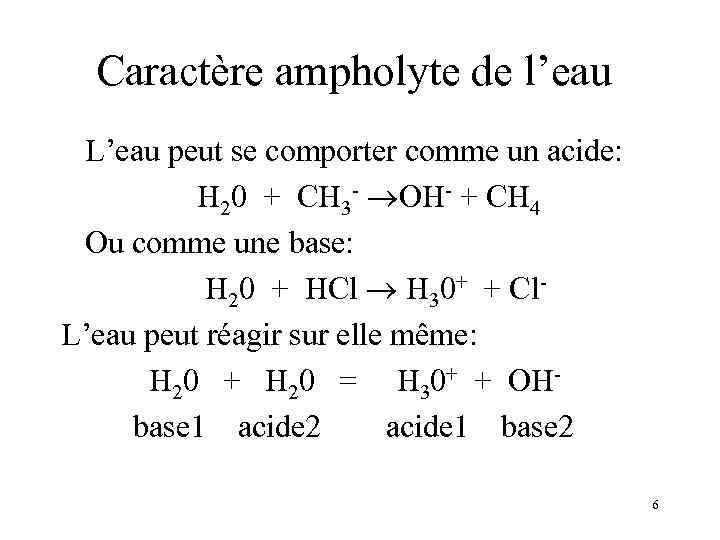
Caractère ampholyte de l’eau L’eau peut se comporter comme un acide: H 20 + CH 3 - OH- + CH 4 Ou comme une base: H 20 + HCl H 30+ + Cl. L’eau peut réagir sur elle même: H 20 + H 20 = H 30+ + OHbase 1 acide 2 acide 1 base 2 6

Caractère ampholyte de l’eau La dernière réaction est un équilibre dont la constante: Ke = [H 30+][OH-] = 10 -14 à 25 °C Permet de définir les 2 couples de l’eau: - H 3 O+/H 2 O où H 3 O+ est l’acide - H 2 O /OH- où H 2 O est l’acide 7

II. Réaction des acides et des bases dans l’eau i. Caractère ampholyte de l’eau ii. Mise en solution d’un acide dans l’eau 8

ii. Mise en solution d’un acide dans l’eau La réaction mise en œuvre est: AH + H 20 = A- + H 30+ (1) qui est caractérisée par une constante d’équilibre (constante d’acidité): Ka = [A-][H 30+]/[AH] Si Ka est supérieure à 1, l’acide est fort AH + H 20 A- + H 30+ Sinon on vérifie l’équilibre (1) 9

iii. Mise en solution d’une base dans l’eau La réaction mise en œuvre est: B + H 20 = BH+ + 0 H- (2) qui est caractérisée par une constante d’équilibre (constante de basicité): Kb = [BH+][0 H-]/[B] Si Kb est supérieure à 1, la base est forte B + H 20 BH+ + 0 HSinon on vérifie l’équilibre (2) 10

II. Réaction des acides et des bases dans l’eau i. Caractère ampholyte de l’eau ii. Mise en solution d’un acide dans l’eau iii. Force des espèces conjuguées 11

iii. Force des espèces conjuguées Si AH est un acide faible: AH + H 20 = A- + H 30+ (1) avec: Ka = [A-][H 30+]/[AH] Mais, A- est une base faible qui donne: A- + H 20 = AH + 0 H- (2) avec: Kb = [AH][0 H-]/[A-] Et : Ka. Kb = [H 30+][0 H-] = Ke = 10 -14 12

iii. Force des espèces conjuguées Ka et Kb de sa base conjuguée varient en sens inverse Kb = Ke/Ka. En général, on ne donne pas les valeurs de Kb, mais on donne celle de Ka pour l’acide conjugué Exemple: Ka de CH 3 COOH = 10 -4, 7 Et Kb de CH 3 COO- = 10 -9, 3 13

II. Réaction des acides et des bases dans l’eau i. iii. iv. Caractère ampholyte de l’eau Mise en solution d’un acide dans l’eau Force des espèces conjuguées Effet de nivellement de l’eau 14

iv. Effet de nivellement de l’eau Lorsqu’on met un acide fort dans l’eau, il se transforme intégralement en H 30+ AH + H 20 A- + H 30+ est donc l’acide le plus fort qui peut exister dans l’eau 15

iv. Effet de nivellement de l’eau Lorsqu’on met une base forte dans l’eau, elle se transforme intégralement en 0 HB + H 20 BH+ + 0 H 0 H- est donc la base la plus forte qui peut exister dans l’eau 16

II. Réaction des acides et des bases dans l’eau i. iii. iv. v. Caractère ampholyte de l’eau Mise en solution d’un acide dans l’eau Force des espèces conjuguées Effet de nivellement de l’eau Définition de l’opérateur p 17

v. Définition de l’opérateur p Les grandeurs impliquées en chimie en solution sont peu significatives: Ke = 10 -14; Ka(CH 3 COOH) = 10 -4, 7 les concentrations sont souvent de 10 -2 ou 10 -3 mol/L On définit p. X = - log. X 18

v. Définition de l’opérateur p On définit p. X = - log. X Ainsi : pc = - log c p. Ke = - log 10 -14 = 14 p. Ka = - log Ka et p. Kb = -log Kb Il en résulte p. Ka + p. Kb = 14 pour un couple acide-base. Et p. H = -log[H 30+] 19

Plan du cours acides-base I. II. Définition de BRONSTED Réaction des acides et des bases dans l’eau III. Calcul du p. H de quelques solutions 20

III. Calcul du p. H de quelques solutions i. Démarche générale Méthode de la réaction prépondérante (RP) • Elle fixe le milieu • Elle met en œuvre les 2 espèces les plus fortes • On considère une espèce négligeable si elle est sous le seuil des 10% 21

III. Calcul du p. H de quelques solutions i. Démarche générale ii. p. H de l’eau pure 22

ii. p. H de l’eau pure Dans l’eau pure: - l’acide le plus fort est l’eau - La base la plus forte est l’eau Donc la RP est: H 20 + H 20 = H 30+ + OHtin / / 0 0 teq / / x x Ke = x 2 = 10 -14 d’où: c = 10 -7 mol/L et p. H = 7 23

III. Calcul du p. H de quelques solutions i. Démarche générale ii. p. H de l’eau pure iii. p. H d’une solution d’acide fort 24

iii. p. H d’une solution d’acide fort Un acide fort se dissocie totalement dans l’eau: AH + H 20 A- + H 30+ tin c / 0 0 On ne prend pas encore en compte l’eau tfin 0 / c c On a [H 30+] = c et p. H = - log c 25

iii. p. H d’une solution d’acide fort Cas particulier: c faible (<10 -6, 5 mol/L). La dissociation de l’eau n’est pas négligeable H 20 + H 20 = H 30+ + OHtin / / c 0 teq / / c+x x Il vient: Ke = (c + x) x ou x 2 + cx – Ke = 0 Sauf si c < 10 -8 mol/L car x >> c Et (c + x) x d’où Ke x 2 et p. H = 7 26

III. Calcul du p. H de quelques solutions i. iii. iv. Démarche générale p. H de l’eau pure p. H d’une solution d’acide fort p. H d’une solution de base forte 27

iv. p. H d’une solution de base forte Une base forte se dissocie totalement dans l’eau: B + H 20 OH- + BH+ tin c / 0 0 On ne prend pas encore en compte l’eau tfin 0 / c c On a [OH-] = c et [H 30+] = Ke/c p. H = - log (Ke/c) = 14 + log c 28

iv. p. H d’une solution de base forte Cas particulier: c faible (<10 -6, 5 mol/L). La dissociation de l’eau n’est pas négligeable H 20 + H 20 = H 30+ + OHtin / / 0 c teq / / y c+y Il vient: Ke = (c + y) y ou y 2 + cy – Ke = 0 Sauf si c < 10 -8 mol/L car y >> c Et (c + y) y d’où Ke y 2 et p. H = 7 29

III. Calcul du p. H de quelques solutions i. iii. iv. v. Démarche générale p. H de l’eau pure p. H d’une solution d’acide fort p. H d’une solution de base forte p. H d’une solution d’acide faible 30

v. p. H d’une solution d’acide faible Un acide faible est partiellement dissocié H 20 + AH = H 30+ + Atin / c 0 0 teq / c - x x x Et Ka = x 2/(c – x) On peut souvent faire c >> x Ka x 2/c Ou x = [H 30+] = (c. Ka)1/2 C’est à dire p. H = 1/2 (pc + p. Ka) 31

v. p. H d’une solution d’acide faible L’approximation c >> x suppose x < c/10 Ka = x 2/c Ka < c/100 ou encore p. Ka – pc > 2 Si on ne remplit pas cette condition, il faut résoudre : Ka = x 2/(c – x) x 2 + Ka. x – Ka. c = 0 qui donne x = [H 30+] 32

III. Calcul du p. H de quelques solutions i. iii. iv. v. vi. Démarche générale p. H de l’eau pure p. H d’une solution d’acide fort p. H d’une solution de base forte p. H d’une solution d’acide faible p. H d’une solution de base faible 33

vi. p. H d’une solution de base faible Une base faible est partiellement protonée B + H 20 = BH+ + 0 Htin c / 0 0 teq c - y / y y Et Kb = y 2/(c – y) On peut souvent faire c >> y Kb y 2/c Ou y = [0 H-]= Ke/[H 30+] = (c. Kb)1/2 C’est à dire p. H = 14 - ½ (pc + p. Kb) p. Ka + p. Kb = 14 p. H = 7 – ½ pc + ½ p. Ka 34

vi. p. H d’une solution de base faible L’approximation c >> y suppose y < c/10 Kb = y 2/c Kb < c/100 ou encore p. Kb – pc > 2 Si on ne remplit pas cette condition, il faut résoudre : Kb = y 2/(c – y) y 2 + Kb. y – Kb. c = 0 qui donne y = [0 H-] = Ke/[H 30+] 35

Plan du cours acides-base I. Définition de BRONSTED II. Réaction des acides et des bases dans l’eau III. Calcul du p. H de quelques solutions IV. Abondance relative des espèces 36

IV. Abondance relative des espèces On transforme Ka = [H 30+][A-]/[AH] en : [H 30+] = Ka. [AH]/[A-] Ou encore en: p. H - p. Ka = - log ([AH]/[A-]) On remarque que: • Si p. H = p. Ka [AH] = [A-] • Si p. H < p. Ka [AH] > [A-] • Si p. H > p. Ka [AH] < [A-] 37

IV. Abondance relative des espèces Si on fait une approche quantitative: [AH]/[A-] > 10 si p. H < p. Ka – 1 [AH]/[A-] > 100 si p. H < p. Ka – 2 [AH]/[A-] < 0, 1 si p. H > p. Ka – 1 [AH]/[A-] < 0, 01 si p. H > p. Ka – 2 On peut regrouper cela dans le graphique: 38

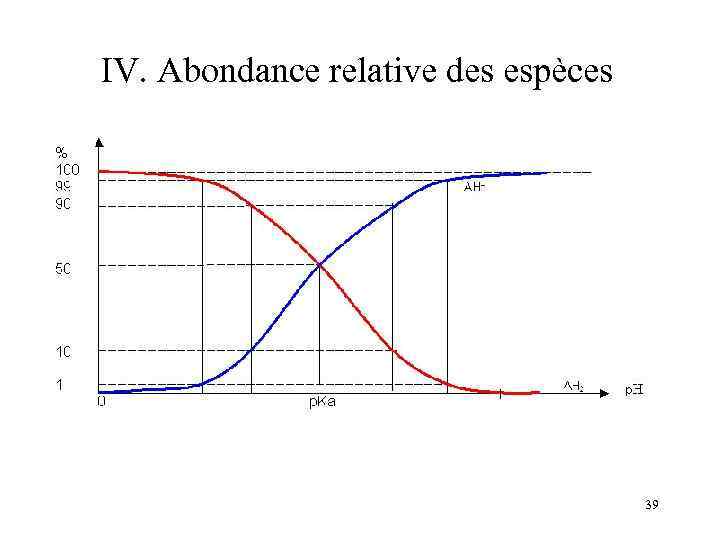
IV. Abondance relative des espèces 39

IV. Abondance relative des espèces Dans le cas d’un diacide AH 2, il y a 2 acidités distinctes: • H 20 + AH 2 = H 30+ + AHKa 1 = [AH-][H 30+]/[AH 2] • H 20 + AH- = H 30+ + A 2 Ka 2 = [A 2 -][H 30+]/[AH-] On a toujours Ka 1 > Ka 2 40

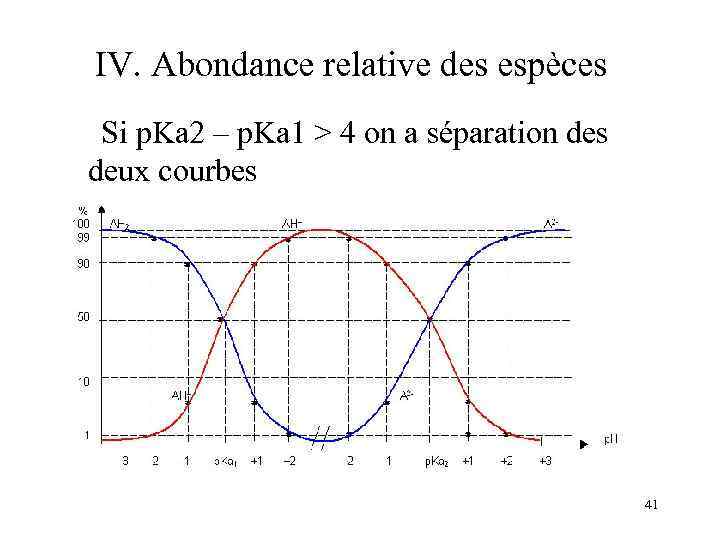
IV. Abondance relative des espèces Si p. Ka 2 – p. Ka 1 > 4 on a séparation des deux courbes 41

Plan du cours acides-base I. Définition de BRONSTED II. Réaction des acides et des bases dans l’eau III. Calcul du p. H de quelques solutions IV. Abondance relative des espèces V. Dosage d’un acide faible par une base faible 42

V. Dosage d’un acide faible par une base faible En réalité, évolution du p. H avec des proportions variables de base et d’acide On dispose d’un volume fixe de solution d’acide de concentration connue: Na = ca. Va (fixe) et d’un volume variable de base de concentration connue: Nb = cb. Vb (variable) 43

V. Dosage d’un acide faible par une base faible i. Calcul de la constante d’équilibre du dosage (1) C’est le premier calcul à mener: • Constante petite (pas de réaction) • Constante grande (réaction effective) 44

i. Calcul de la constante d’équilibre du dosage La réaction de dosage s’écrit: AH + B = A- + BH+ K = [A-]/[AH]. [BH+]/[B] K = ([A-][H 30+]/[AH]). ([BH+]/[B][H 30+]) K = Ka(AH)/Ka(BH+) Si BH+ est un acide plus fort que AH la réaction n’a pas lieu de façon importante 45

i. Calcul de la constante d’équilibre du dosage Si la constante est faible AH + B = A- + BH+ tin c c’ 0 0 teq c-x c’-x x x N. B: c = Na/(Va+ Vb) et c’ = Nb/(Va+ Vb) K = x 2/(c-x)(c’-x) Puis Ka(AH) = x[H 30+]/(c-x) ou Ka(BH+) = x[H 30+]/(c’-x) Qui donne [H 30+] et donc le p. H 46

V. Dosage d’un acide faible par une base faible i. Calcul de la constante d’équilibre du dosage ii. Établissement de la courbe de titrage 47

ii. Établissement de la courbe de titrage • • Si K est grande, la réaction se fait et le p. H évolue avec les proportions d’acide et de base. On considèrera 4 cas: Vb = 0 (il n’y a que de l’acide) Vb tel que Na > Nb (l’acide est en excès) Vb tel que Na = Nb (point d’équivalence) Vb tel que Na < Nb (l’acide est en défaut) 48

ii. Établissement de la courbe de titrage • Vb = 0 (il n’y a que de l’acide) On est dans le cas d’une solution d’acide faible AH: si p. Ka – pc > 2 on a p. H = ½ (p. Ka + pc) avec c = ca 49

ii. Établissement de la courbe de titrage • Vb tel que Na > Nb (l’acide est en excès) la réaction: AH + B A- + BH+ tin c c’ 0 0 teq c-c’ 0 c’ c’ consomme toute la base; il reste donc AH, Aet BH+. Ka(AH) = [A-][H 3 O+]/[AH] p. H = p. Ka(AH) – log([AH]/[A-]) Ou p. H = p. Ka(AH) – log(c’/(c-c’)) 50

ii. Établissement de la courbe de titrage • Vb tel que Na = Nb (point d’équivalence Ve) La réaction: AH + B = A- + BH+ tin c c 0 0 teq c c Permet d’affirmer que [AH] = [B] et que [A-] = [BH+] Et en faisant Ka(AH). Ka(BH+) Il vient 51

Établissement de la courbe de titrage Ka(AH). Ka(BH+) = [A-][H 3 O+]/[AH]. [B][H 3 O+]/[BH+] Ou Ka(AH). Ka(BH+) = [H 3 O+]2 C’est à dire p. H = ½ (p. Ka(AH) + p. Ka(BH+) ) Cette valeur est indépendante des concentrations 52

Établissement de la courbe de titrage • Vb tel que Na < Nb (l’acide est en défaut) la réaction: AH + B A- + BH+ tin c c’ 0 0 teq 0 c’- c consomme tout l’acide; il reste donc B, A- et BH+. Ka(BH+) = [B][H 3 O+]/[BH+] p. H = p. Ka(BH+) – log([BH+]/[B]) Ou p. H = p. Ka(BH+) – log(c/(c’-c)) 53

Établissement de la courbe de titrage ATTENTION: les valeurs c (pour l’acide) et c’ (pour la base) sont celles qui sont observées dans le mélange. On a ainsi dans tout ce qui précède: c = Na/Vt = ca. Va/(Va+Vb) et c’ = Nb/Vt = cb. Vb/(Va+Vb) 54

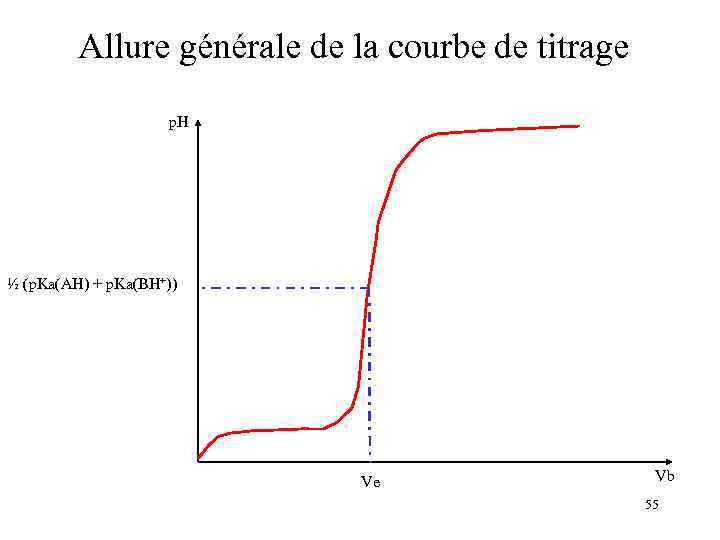
Allure générale de la courbe de titrage p. H ½ (p. Ka(AH) + p. Ka(BH+)) Ve Vb 55

Plan du cours acides-base I. Définition de BRONSTED II. Réaction des acides et des bases dans l’eau III. Calcul du p. H de quelques solutions IV. Abondance relative des espèces V. Dosage d’un acide faible par une base faible VI. Les solutions tampons 56

VI. Les solutions tampons i. • • Définition Son p. H varie peu quand on: La dilue (même de façon importante) Lui ajoute de l’acide ou de la base On l’obtient en préparant un mélange d’un acide faible AH et de sa base conjuguée A- 57

VI. Les solutions tampons i. Définition ii. Préparation On doit fixer le p. H visé; par exemple pour un p. H de 4, 8 avec le couple CH 3 COOH et CH 3 COO-: Ka(CH 3 COOH) = [CH 3 COO-][H 3 O+]/[CH 3 COOH ] p. H = p. Ka(CH 3 COOH) – log([CH 3 COOH ]/ [CH 3 COO-] p. H = 4, 7 – log([CH 3 COOH ]/ [CH 3 COO-] = - 0, 1 [CH 3 COOH ]/ [CH 3 COO-] = 1, 25 58

VI. Les solutions tampons i. Définition ii. Préparation iii. Mesure de l’effet tampon 59

iii. Mesure de l’effet tampon On va considérer l’effet de l’addition de 10 -3 mol. d’acide chlorhydrique dans: 1. 1 L d’eau, 2. 1 L de solution contenant 10 -2 mol. de CH 3 COOH et de CH 3 COO 3. 1 L de solution contenant 10 -1 mol. de CH 3 COOH et de CH 3 COO 60

iii. Mesure de l’effet tampon • Addition dans l’eau pure: p. H initial: 7 p. H après addition de 10 -3 mol. De HCl: 3 Variation de p. H = 3 – 7 = -4 61

iii. Mesure de l’effet tampon • Addition dans la solution à 10 -2 mol/L: p. H initial donné par p. H = p. Ka – log([AH]/[A-]) p. H initial = 4, 7 L’addition de HCl (en réalité H 3 O+) provoque A- + H 3 O+ AH + H 2 O tin 10 -2 10 -3 10 -2 / teq 9. 10 -3 traces 11. 10 -3 / D’où p. H = 4, 7 – log(11/9) = 3, 75 Soit une variation de p. H de : - 0, 95 62

iii. Mesure de l’effet tampon • Addition dans la solution à 10 -1 mol/L: p. H initial donné par p. H = p. Ka – log([AH]/[A-]) p. H initial = 4, 7 (identique au précédent) L’addition de HCl (en réalité H 3 O+) provoque A- + H 3 O+ AH + H 2 O tin 10 -1 10 -3 10 -1 / teq 99. 10 -3 traces 101. 10 -3 / D’où p. H = 4, 7 – log(101/99) = 4, 7 Soit une variation de p. H de : - 0, 01 63

VI. Les solutions tampons i. iii. iv. Définition Préparation Mesure de l’effet tampon Commentaires 64

iv. Commentaires L’effet tampon est d’autant plus important que les espèces acides et basiques sont: • plus concentrées, • ont des concentrations voisines. 65