Лекция 5 Delphi условия и алгоритмы.ppt
- Количество слайдов: 21

Леонардо Пизанским, известным как Фибоначчи, была исследована последовательность. Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что: • В «нулевом» месяце имеется пара кроликов (1 новая пара). • В первом месяце первая пара производит на свет другую пару (1 новая пара). • Во втором месяце обе пары кроликов порождают другие пары и первая пара погибает (2 новые пары). • В третьем месяце вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (3 новые пары). Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает. Пусть популяция за месяц n будет равна F(n). Таким образом общее количество пар будет равно F(n) = F(n-1) + F(n-2).

На интервале (1000. . 9999) найти все числа, каждое из которых обладает тем свойством, что сумма первой и второй цифр записи этого числа равна сумме третьей и четвёртой цифр. Особенность: вместо выделения цифр «в лоб» , или перебором цикла, можно преобразовать число i в строковый тип, (Z=inttostr(i)) и обратиться к ней, как к элементам массива: Z[1]+Z[2]=Z[3]+Z[4] Алгоритмы

Определить наименьшее число, которое при делении на 2, 3, 4, 5, 6, 7, 8, 9 дает одинаковые остатки = 1. Подсказка. 1. Вариант. Задайте некоторое число, до которого будет выполнен перебор (для реализации безусловного цикла). 2. Вариант. Задайте условие, пока не выполнен поиск искомого числа, выполняем цикл. Основное проверяемое условие: в цикле ищем остаток от деления и проверяем, равен ли он 0. Если таких остатков 8 – число найдено. Алгоритмы

Найти все простые делители натурального числа N. J – максимальный индекс простого числа. for i: =1 to j do if n mod Prost[i]=0 then edit 1. text: =edit 1. text+’ ’+(Prost[i], ' ');

Алгоритм. Решето Эрастофена. Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги: 1. Выписать подряд все целые числа от двух до n (2, 3, 4, …, n). 2. Пусть переменная p изначально равна двум — первому простому числу. 3. Считая от p шагами по p, зачеркнуть в списке все числа от 2 p до n кратные p (то есть числа 2 p, 3 p, 4 p, …) 4. Найти первое не зачеркнутое число, большее чем p, и присвоить значению переменной p это число. 5. Повторять шаги 3 и 4 до тех пор, пока p не станет больше, чем n Теперь все не зачеркнутые числа в списке — простые.

Вход: натуральное число n Пусть A — булевый массив, индексируемый числами от 2 до n, изначально заполненный значением true. count = n - 1 для i = 2, 3, 4, . . . , пока i ^2 ≤ n: если A[i] = true: для j = i ^2, i ^2 + i, i ^2 + 2 i, . . . , пока j ≤ n: если A[j] = true: A[j] = false count = count - 1 Теперь все числа i, такие что A[i] = true, являются простыми, а переменная count содержит в себе их общее количество в массиве.

Женщина шла на базар и разбила яйца, лежавшие у неё в корзине Она сказала, что не знает сколько яиц у неё было, но когда она брала по 2, 3, 4, 5 и 6 яиц то оставалось в остатке одно. Когда же она брала по 7 яиц , то ничего не оставалось в остатке. Сколько яиц могло быть в корзине ? for i: =1 to 5000 do if (i mod 2=1)and(i mod 3=1)and (i mod 4=1)and(i mod 5=1)and (i mod 6=1)and(i mod 7=0)then begin edit 1. text: ='может быть: ’+inttostr(i); end; edit 2. text: ='Ну смотря какая у женщины корзина!’;

http: //www. sorting-algorithms. com Сортировака массивов Обменные Пузырьком • Перемешиванием • Гномья • Быстрая • Расчёской Выбором • Пирамидальная Вставками • Шелла • Деревом Слиянием • Без дополнительной памяти Без сравнений Подсчётом • Поразрядная • Блочная Гибридные Introsort Прочее Топологическая • Сети Непрактичные Bogosort • Stooge sort • Глупая • Блинная

Оценка алгоритма сортировки Алгоритмы сортировки оцениваются по скорости выполнения и эффективности использования памяти: Время — основной параметр, характеризующий быстродействие алгоритма. Называется также вычислительной сложностью. Для упорядочения важны худшее, среднее и лучшее поведение алгоритма. Для типичного алгоритма хорошее поведение — это O(n log n) и плохое поведение — это O(n 2). Идеальное поведение для упорядочения — O(n). Память - ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. Как правило, эти алгоритмы требуют O(log n) памяти

Ещё одним важным свойством алгоритма является его сфера применения. Здесь основных типов упорядочения два: Внутренняя сортировка оперирует с массивами, целиком помещающимися в оперативной. В современных архитектурах персональных компьютеров широко применяется подкачка и кэширование памяти. Алгоритм сортировки должен хорошо сочетаться с применяемыми алгоритмами кэширования и подкачки. Внешняя сортировка оперирует с запоминающими устройствами большого объёма, но с доступом не произвольным, а последовательным (упорядочение файлов Также алгоритмы классифицируются по: • потребности в дополнительной памяти или её отсутствии • потребности в знаниях о структуре данных, выходящих за рамки операции сравнения, или отсутствии таковой

Сортировка простыми обменами, сортиро вка пузырько м (bubble sort) — простой алгоритм сортировки. Для понимания и реализации этот алгоритм — простейший, но эффективен он лишь для небольших массивов. Сложность алгоритма: O(n²). Алгоритм считается учебным и практически не применяется вне учебной литературы, вместо него на практике применяются более эффективные алгоритмы сортировки. В то же время метод сортировки обменами лежит в основе некоторых более совершенных алгоритмов, таких как шейкерная сортировка, сортировка Шелла и быстрая сортировка. Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает — массив отсортирован. При проходе алгоритма, элемент, стоящий не на своём месте, «всплывает» до нужной позиции как пузырёк в воде, отсюда и название алгоритма.
![Вход: массив A, состоящий из элементов A[1], A[2], . . . , A[n-1], A[n] Вход: массив A, состоящий из элементов A[1], A[2], . . . , A[n-1], A[n]](https://present5.com/presentation/20070619_133096961/image-12.jpg)
Вход: массив A, состоящий из элементов A[1], A[2], . . . , A[n-1], A[n] t : = истина цикл пока t: t : = ложь цикл для j = 1, 2, . . . , n − 1: если A[j] > A[j+1], то: обменять местами элементы A[j] и A[j+1] t : = истина Булевая переменная t используется для того, чтобы определить, был ли произведён хотя бы один обмен на очередной итерации внешнего цикла. Алгоритм останавливается, когда таких обменов не было. Алгоритм можно немного улучшить следующими способами: Внутренний цикл можно выполнять для j = 1, 2, . . . , n − i, где i — номер итерации внешнего цикла (нумерация с единицы), так как на i-й итерации последние i элементов массива уже будут правильно упорядочены. Внутренний цикл можно модифицировать так, чтобы он поочерёдно просматривал массив то с начала, то с конца. Модифицированный таким образом алгоритм называется сортировкой перемешиванием или шейкерной сортировкой.
Первый проход: (5 1 4 2 8) (1 5 4 2 8), Здесь алгоритм сравнивает два первых элемента и меняет их местами. (1 5 4 2 8) (1 4 5 2 8), Меняет местами, так как 5 > 4 (1 4 5 2 8) (1 4 2 5 8), Меняет местами, так как 5 > 2 (1 4 2 5 8), Теперь, ввиду того, что элементы стоят на своих местах (8 > 5), алгоритм не меняет их местами. Второй проход: (1 4 2 5 8) (1 2 4 5 8), Меняет местами, так как 4 > 2 (1 2 4 5 8) Теперь массив полностью отсортирован, но алгоритм не знает так ли это. Повторим) http: //www. cs. ubc. ca/~harrison/Java/sorting-demo. html

Сортировка вставками — простой алгоритм сортировки. Хотя этот алгоритм сортировки уступает в эффективности более сложным (таким как быстрая сортировка), у него есть ряд преимуществ: эффективен на небольших наборах данных, на наборах данных до десятков элементов может оказаться лучшим; эффективен на наборах данных, которые уже частично отсортированы; это устойчивый алгоритм сортировки (не меняет порядок элементов, которые уже отсортированы); может сортировать список по мере его получения; использует O(1) временной памяти, включая стек. Минусом же является высокая сложность алгоритма: O(n²). На каждом шаге алгоритма мы выбираем один из элементов входных данных и вставляем его на нужную позицию в уже отсортированном списке, до тех пор, пока набор входных данных не будет исчерпан. Метод выбора очередного элемента из исходного массива произволен. Обычно (и с целью получения устойчивого алгоритма сортировки), элементы вставляются по порядку их появления во входном массиве.

Время выполнения алгоритма зависит от входных данных: чем большее множество нужно отсортировать, тем большее время выполняется сортировка. Также на время выполнения влияет исходная упорядоченность массива. Так, лучшим случаем является отсортированный массив, а худшим — массив, отсортированный в порядке, обратном нужному. Вход: массив A, состоящий из элементов A[1], A[2], . . . , A[n] for i = 2, 3, . . . , n: key : = A[i] j : = i - 1 while j >= 0 and A[j] > key: A[j + 1] : = A[j] j : = j - 1 A[j + 1] : = key

Быстрая сортировка (англ. quicksort), часто называемая qsort по имени реализации в стандартной библиотеке языка Си — широко известный алгоритм сортировки, разработанный английским информатиком Чарльзом Хоаром в 1960 году. Один из быстрых известных универсальных алгоритмов сортировки массивов (в среднем O(n log n) обменов Краткое описание: выбрать элемент, называемый опорным. сравнить все остальные элементы с опорным, на основании сравнения разбить множество на три — «меньшие опорного» , «равные» и «большие» , расположить их в порядке меньшиеравные-большие. повторить рекурсивно для «меньших» и «больших» .
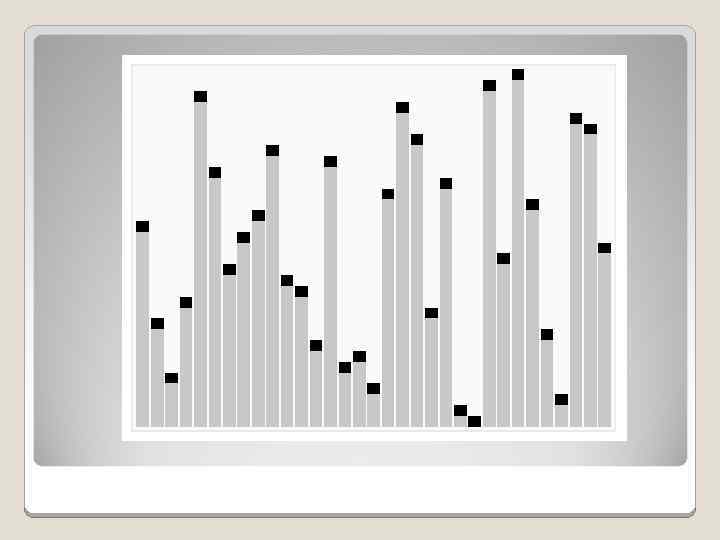

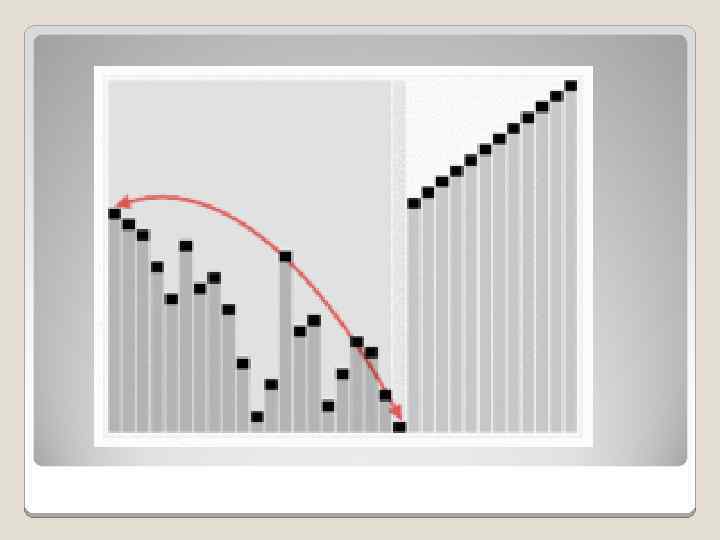
Пирамидальная сортировка — алгоритм сортировки, работающий в худшем, в среднем и в лучшем случае (то есть гарантированно) за Θ(n log n) операций при сортировке n элементов. Может рассматриваться как усовершенствованная сортировка пузырьком. Сортировка пирамидой использует сортирующее дерево. Сортирующее дерево — это такое двоичное дерево, у которого выполнены условия: Каждый лист имеет глубину либо d, либо d − 1, d — максимальная глубина дерева. Значение в любой вершине больше, чем значения её потомков. Достоинства: Имеет доказанную оценку худшего случая O(nlogn). Требует всего O(1) дополнительной памяти (если дерево организовывать так, как показано выше). Недостатки Сложен в реализации, неустойчив, на почти отсортированных массивах работает столь же долго, как и на хаотических, плохо сочетается с кэшированием и подкачкой. Из-за сложности алгоритма выигрыш получается только на больших n>10000.

Нерациональные сортировки: Блинная сортировка. Единственная операция, допустимая в алгоритме — переворот элементов последовательности до какого-либо индекса. В отличие от традиционных алгоритмов, в которых минимизируют количество сравнений, в блинной сортировке требуется сделать как можно меньше переворотов. Процесс можно визуально представить как стопку блинов, которую тасуют путём взятия нескольких блинов сверху и их переворачивания. Усложнённый вариант представляет собой блинную сортировку, элементы содержат дополнительный бинарный параметр. Эту задачу предложили Билл Гейтс и Христос Пападимитриоу в 1979 году. Она стала известна как «задача о подгоревших блинах» Каждый блин в стопке подгорел с одной стороны. Требуется отсортировать блины по возрастанию (убыванию) диаметра так, чтобы они все лежали на тарелке подгоревшей стороной вниз. В 2007 году группа студентов создала биологический компьютер на основе генетически модифицированной кишечной палочки, который решал задачу о подгорелых блинах.

Bogosort (также случайная сортировка, сортировка ружья или обезьянья сортировка) является очень неэффективным алгоритмом сортировки. . Если bogosort использовать для сортировки колоды карт, то сначала в алгоритме нужно проверить, лежат ли все карты по порядку, и если не лежат, то подбросить колоду в воздух, проверить лежат ли теперь все карты по порядку, и повторять процесс, пока не отсортируется колода. При работе 4 -ядерного процессора 2. 4 ГГц (9. 6 млрд операций в секунду) 18 19 20 7. 6 лет 160 лет 17 7. 29 сут Колода в 32 карты будет сортироваться компьютером лет. 16 139 дней 15 9. 7 часов 8. 4 с 14 33. 6 мин 13 2. 1 мин 12 0. 59 с 0. 0037 с Средне е время 11 0. 045 с Кол-во элемент 10 ов
Лекция 5 Delphi условия и алгоритмы.ppt