LENGUAJES FORMALES Y AUTOMATAS Lenguajes

LENGUAJES FORMALES Y AUTOMATAS • • • Lenguajes regulares. Autómatas finitos. Gramáticas independientes del contexto. Autómatas de pila. Gramáticas generales. Máquinas de Turing.

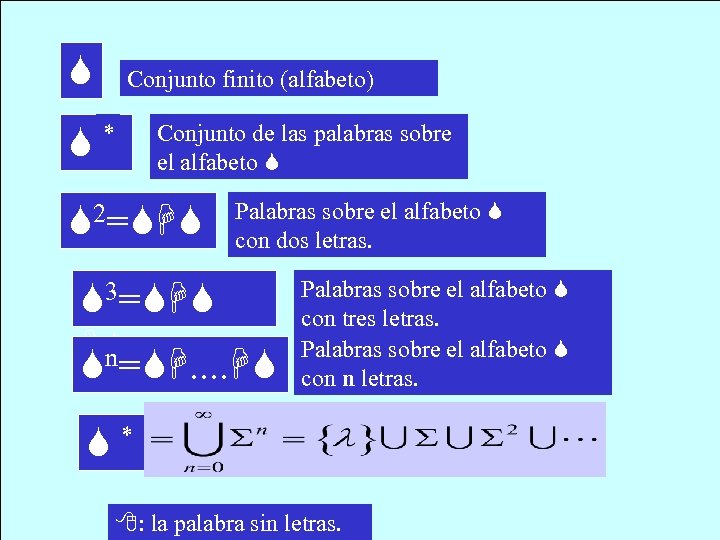Conjunto finito (alfabeto) * Conjunto de las palabras sobre el alfabeto 2= H Palabras sobre el alfabeto con dos letras. 3= H H n= H. . H Palabras sobre el alfabeto con tres letras. Palabras sobre el alfabeto con n letras. * : la palabra sin letras.

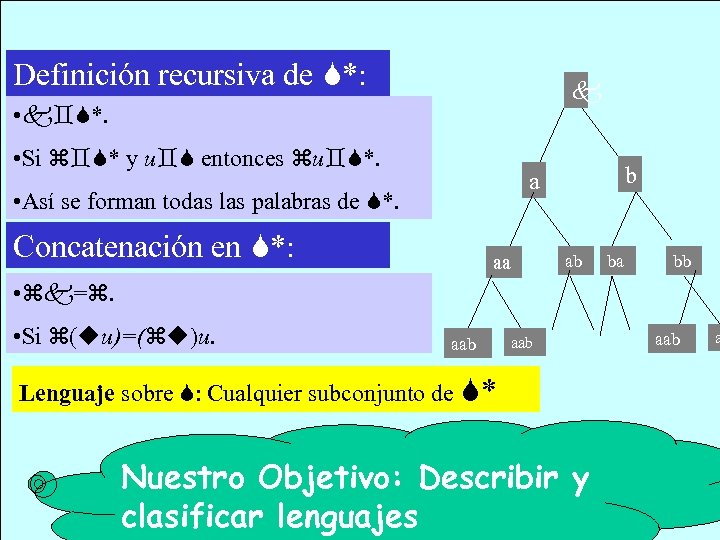Definición recursiva de *: • *. • Si * y u entonces u *. b a • Así se forman todas las palabras de *. Concatenación en *: ab aa ba bb • =. • Si ( u)=( )u. aab Lenguaje sobre : Cualquier subconjunto de * Nuestro Objetivo: Describir y clasificar lenguajes aab a

Expresiones Regulares sobre • es expresión regular • Si u entonces u es expresión regular Si , son expresiones regulares: • ( )* es expresión regular. • ( ) es expresión regular. • ( ) es expresión regular. (ab b)*ab ={a, b} a b (a (ab) ((ab) b b) (((ab) b))* ((((ab) b))*(ab))

Lenguajes asociados a expresiones regulares sobre Expresión regular. Lenguaje regular. • • • u Si , son expresiones regulares: • ( ) • ( )* • {u} A, B Lenguajes regulares:

Ejemplo Expresión regular. (ab b)*ab a b (ab) ((ab) b) (((ab) b))* ((((ab) b))*(ab)) ab abbab abab abbabab bbbab Lenguaje regular ={a, b} {a} {b} { } {ab, b}* Palabras que se escriben con las palabras ab y b {ab, b}* {ab} Palabras que después de cada a tienen una b y terminan con ab babb baabbab

Ejemplos Palabras que contienen exactamente 2 b’s Palabras que contienen 2 o más b’s Palabras que contienen un número par de b’s Palabras que contienen un número impar de b’s a*(ba*ba*)*a* (awb)*ba*ba*ba* (a*ba*b (awb)* )* (a*ba*ba*)* a*ba* (a*b (aw b)* b a* )*

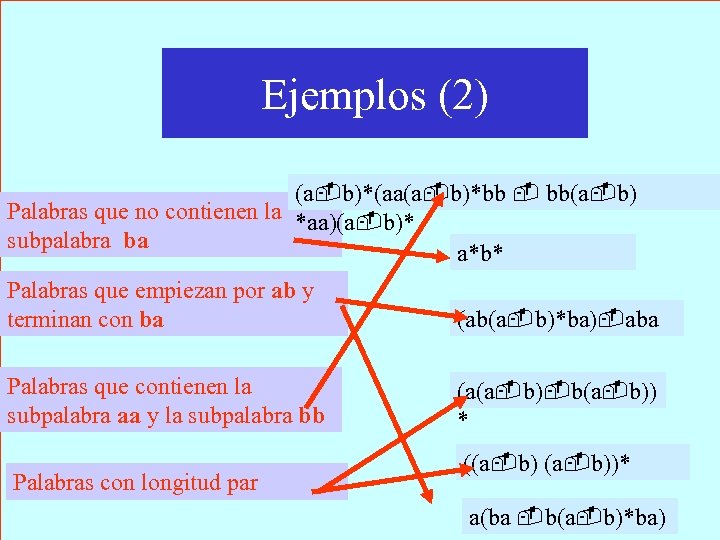Ejemplos (2) (a b)*(aa(a b)*bb bb(a b) Palabras que no contienen la *aa)(a b)* subpalabra ba a*b* Palabras que empiezan por ab y terminan con ba (ab(a b)*ba) aba Palabras que contienen la subpalabra aa y la subpalabra bb (a(a b) b(a b)) * Palabras con longitud par ((a b))* a(ba b(a b)*ba)

Identidades

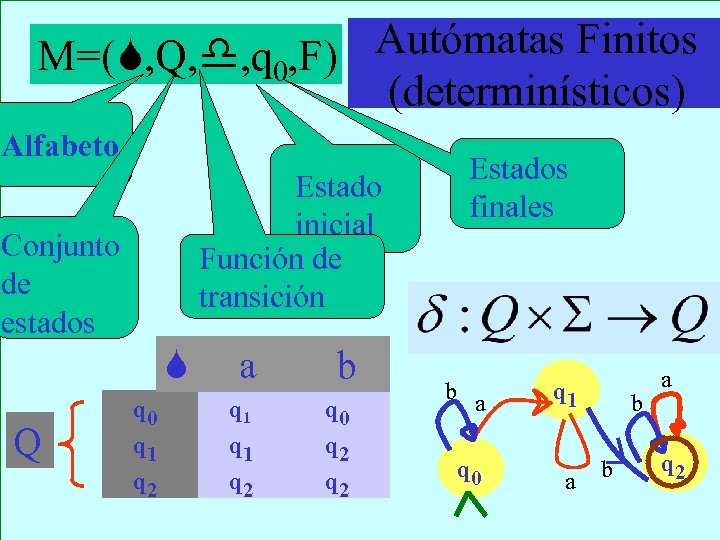Autómatas Finitos M=( , Q, , q 0, F) (determinísticos) Alfabeto Estado inicial Función de transición Conjunto de estados Q q 0 q 1 q 2 a q 1 q 2 b q 0 q 2 Estados finales b a q 0 q 1 a b b a q 2

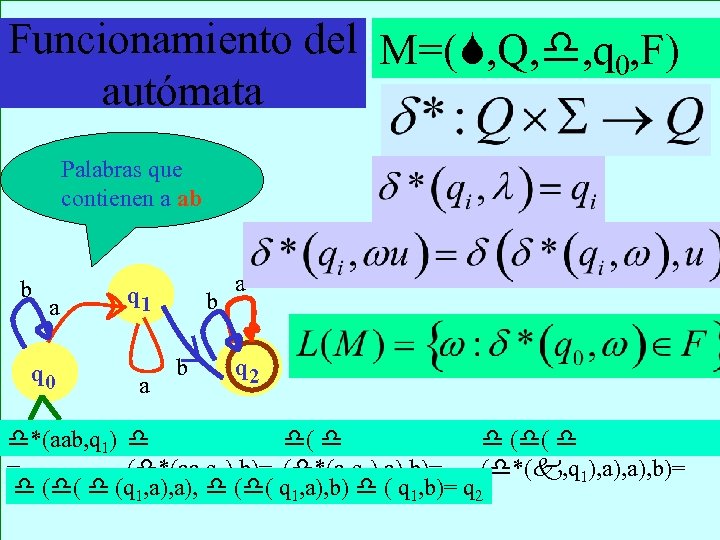Funcionamiento del M=( , Q, , q , F) 0 autómata Palabras que contienen a ab b a q 0 q 1 a b b a q 2 *(aab, q 1) ( ( ( = ( *(aa, q 1), b)= ( *(a, q 1), a), b)= ( *( , q 1), a), b)= ( ( (q 1, a), b)= ( ( q 1, a), b)= ( q 1, b)= q 2

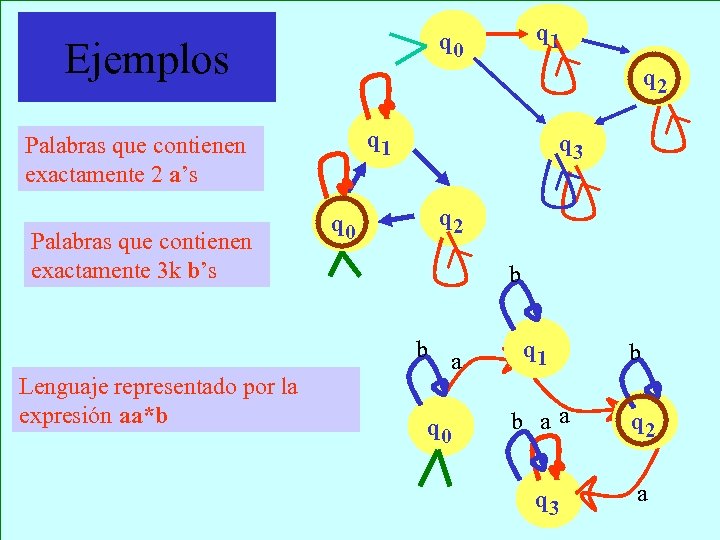Ejemplos q 2 q 1 Palabras que contienen exactamente 2 a’s Palabras que contienen exactamente 3 k b’s Lenguaje representado por la expresión aa*b q 1 q 0 q 3 q 2 b b a q 0 q 1 b b aa q 2 q 3 a

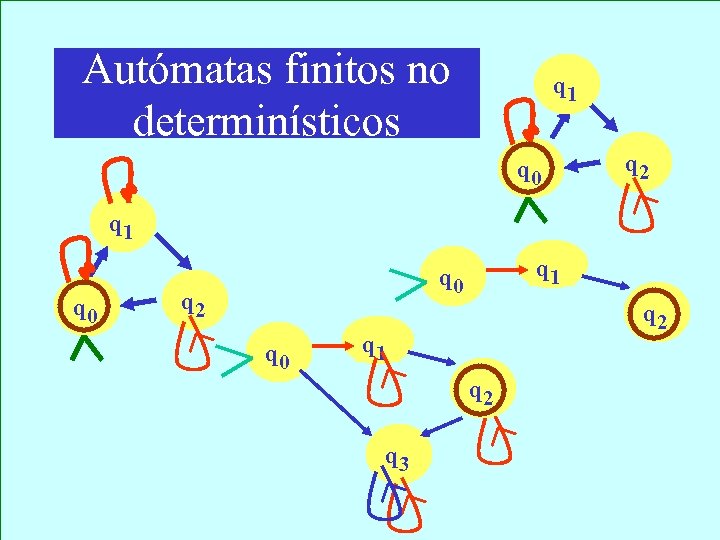Autómatas finitos no determinísticos q 1 q 0 q 2 q 0 q 2 q 1 q 2 q 3

Autómatas finitos no determinísticos Palabras que empiezan por ab y terminan con ba q 0 q 1 q 2 q 5 q 2 q 3 q 4 a(ba wb(awb)*ba)

Lenguajes regulares Expresiones Regulares AFD AFND Gramáticas Regulares No son LR:

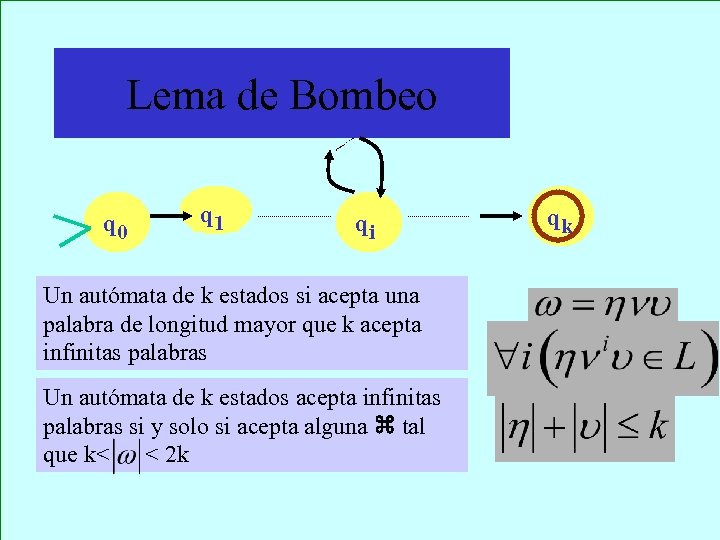Lema de Bombeo q 0 q 1 qi Un autómata de k estados si acepta una palabra de longitud mayor que k acepta infinitas palabras Un autómata de k estados acepta infinitas palabras si y solo si acepta alguna tal que k< < 2 k qk

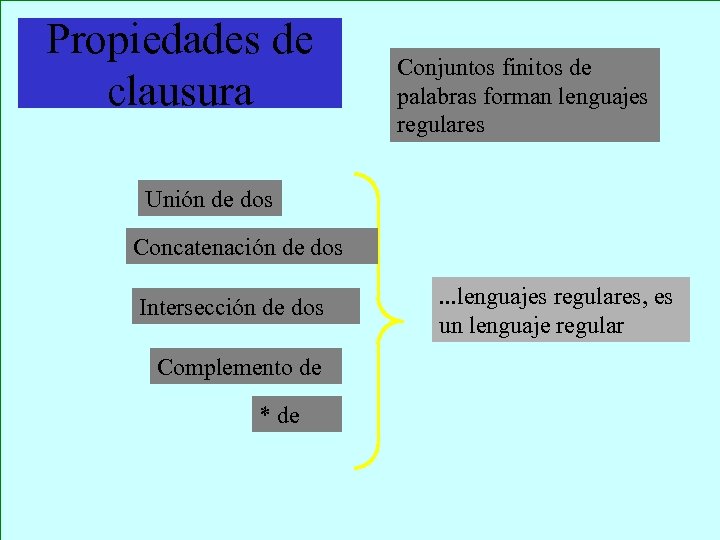Propiedades de clausura Conjuntos finitos de palabras forman lenguajes regulares Unión de dos Concatenación de dos Intersección de dos Complemento de * de . . . lenguajes regulares, es un lenguaje regular

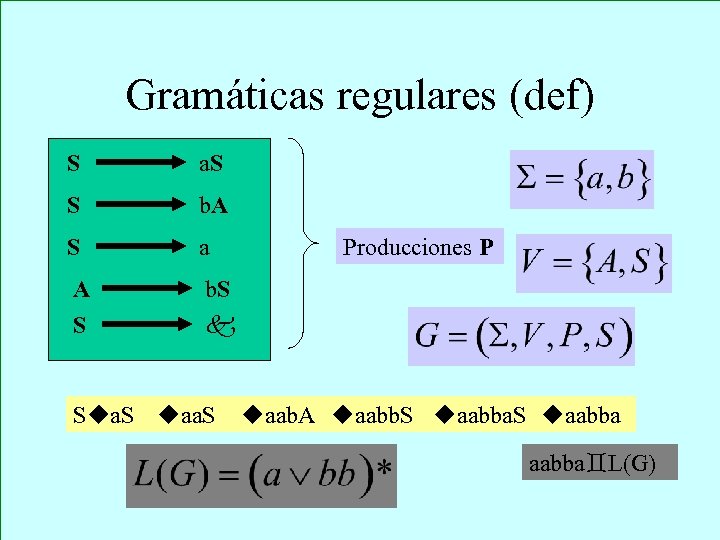Gramáticas regulares (def) S a. S S b. A S a A b. S S S aa. S Producciones P aab. A aabb. S aabba L(G)

Gramáticas regulares (Ejemplo)

Gramáticas Independientes del contexto

Gramáticas Independientes del contexto (ejemplos)

Autómatas de pila M=( , Q, , , q 0, F )

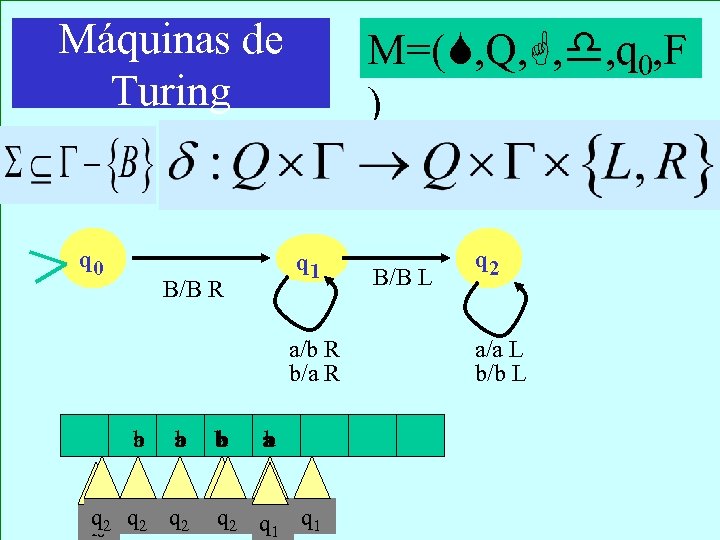Máquinas de Turing q 0 M=( , Q, , , q 0, F ) q 1 B/B R a/b R b/a R b a a b b a b a q 2 2 q q q 02 q 1 q 12 q 1 1 B/B L q 2 a/a L b/b L

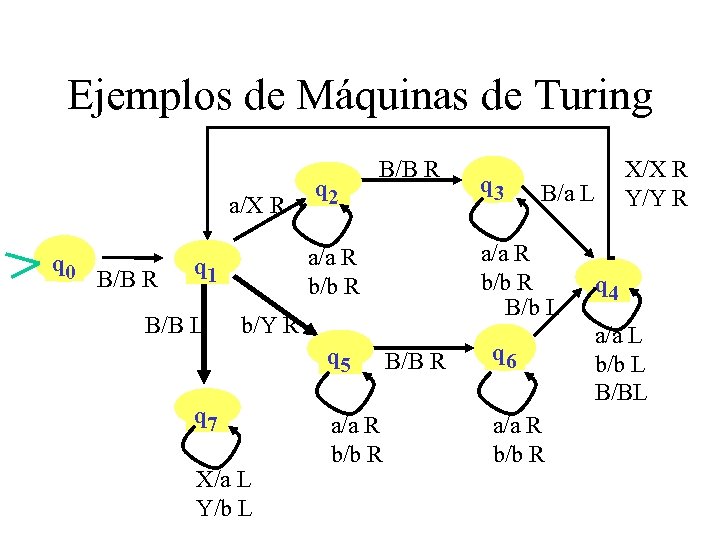Ejemplos de Máquinas de Turing a/X R q 0 B/B R b/Y R q 5 q 7 X/a L Y/b L a/a R b/b R q 3 B/a L a/a R b/b R B/b L a/a R b/b R q 1 B/B L q 2 B/B R q 6 a/a R b/b R X/X R Y/Y R q 4 a/a L b/b L B/BL