Лекции ст тер 2015 3.ppt
- Количество слайдов: 117
 Лектор – Минакова Тамара Сергеевна, профессор кафедры физической и коллоидной химии ТГУ СТАТИСТИЧЕСКАЯ ТЕРМОДИНАМИКА
Лектор – Минакова Тамара Сергеевна, профессор кафедры физической и коллоидной химии ТГУ СТАТИСТИЧЕСКАЯ ТЕРМОДИНАМИКА
 1. Классификация термодинамики Термодинамика Феноменологическая термодинамика Статистическая термодинамика Физическая термодинамика Термодинамика равновесных процессов Химическая термодинамика Термодинамика неравновесных процессов Техническая термодинамика
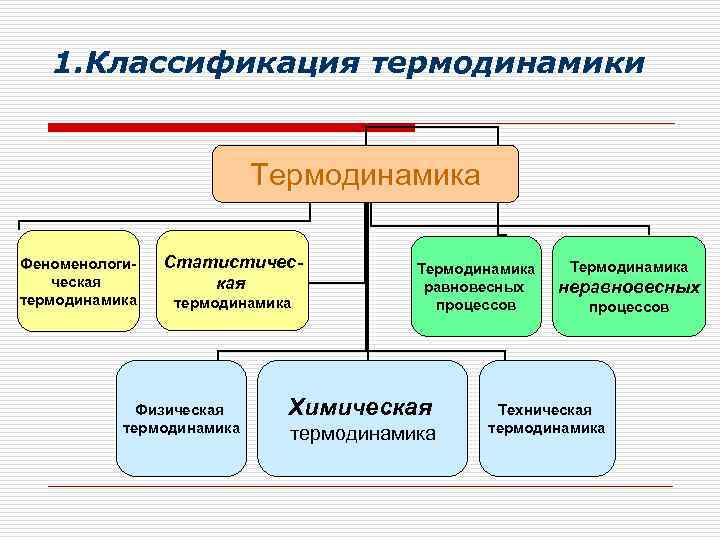
1. Классификация термодинамики Термодинамика Феноменологическая термодинамика Статистическая термодинамика Физическая термодинамика Термодинамика равновесных процессов Химическая термодинамика Термодинамика неравновесных процессов Техническая термодинамика
 1. Классификация термодинамики Феноменологическая термодинамика исходит из ряда установленных на опыте положений и пользуется известными данными о макроскопических свойствах тел. Эта термодинамика не требует внутреннего молекулярного строения и механизма молекулярных процессов в рассматриваемых телах.
1. Классификация термодинамики Феноменологическая термодинамика исходит из ряда установленных на опыте положений и пользуется известными данными о макроскопических свойствах тел. Эта термодинамика не требует внутреннего молекулярного строения и механизма молекулярных процессов в рассматриваемых телах.
 1. Классификация термодинамики a. По характеру используемых параметров системы ( макроскопических или микроскопических) b. По типу процессов – равновесных или неравновесных c. По типу явлений, к которым применима термодинамика
1. Классификация термодинамики a. По характеру используемых параметров системы ( макроскопических или микроскопических) b. По типу процессов – равновесных или неравновесных c. По типу явлений, к которым применима термодинамика
 1. Классификация термодинамики o Статистическая термодинамика использует определённые представления о молекулярном ( атомном ) строении тела. Она использует статистические методы и математический аппарат теории вероятности. Используя спектроскопические данные , она позволяет с высокой точностью рассчитывать термодинамические функции и параметры термодинамического равновесия.
1. Классификация термодинамики o Статистическая термодинамика использует определённые представления о молекулярном ( атомном ) строении тела. Она использует статистические методы и математический аппарат теории вероятности. Используя спектроскопические данные , она позволяет с высокой точностью рассчитывать термодинамические функции и параметры термодинамического равновесия.
 1. Классификация термодинамики o Термодинамика равновесных процессов рассматривает макроскопическое поведение систем, в которых протекают процессы перехода между различными состояниями устойчивого равновесия. Она применима для описания обратимых процессов , скорость которых бесконечно мала и все параметры постоянны времени.
1. Классификация термодинамики o Термодинамика равновесных процессов рассматривает макроскопическое поведение систем, в которых протекают процессы перехода между различными состояниями устойчивого равновесия. Она применима для описания обратимых процессов , скорость которых бесконечно мала и все параметры постоянны времени.
 1. Классификация термодинамики o Термодинамика неравновесных процессов рассматривает реальные процессы , протекающие под воздействием градиентов температур, концентраций, давлений, химических потенциалов. Это различного рода потоки: термические, диффузионные, импульсные и т. д.
1. Классификация термодинамики o Термодинамика неравновесных процессов рассматривает реальные процессы , протекающие под воздействием градиентов температур, концентраций, давлений, химических потенциалов. Это различного рода потоки: термические, диффузионные, импульсные и т. д.
 1. Классификация термодинамики o Физическая термодинамика – применение законов и закономерностей термодинамики к физическим явлениям, телам.
1. Классификация термодинамики o Физическая термодинамика – применение законов и закономерностей термодинамики к физическим явлениям, телам.
 1. Классификация термодинамики o Техническая термодинамика применение законов и закономерностей термодинамики к тепловым машинам.
1. Классификация термодинамики o Техническая термодинамика применение законов и закономерностей термодинамики к тепловым машинам.
 1. Классификация термодинамики o Химическая термодинамика применяет положения и законы общей термодинамики к изучению химических процессов и фазовых переходов, использует термодинамические методы для решения химических задач.
1. Классификация термодинамики o Химическая термодинамика применяет положения и законы общей термодинамики к изучению химических процессов и фазовых переходов, использует термодинамические методы для решения химических задач.
 2. Рекомендуемая литература (основная) 1. А. Г. Стромберг, Д. П. Семченко. Физическая химия. М. : Высшая школа, 2007 . 523 с. 2. Полторак О. М. Термодинамика в физической химии. М. : Высшая школа, 1991. 319 с. 3. В. Д. Ягодовский. Статистическая термодинамика в физической химии. М. : Бином, 2005. 494 с. 4. Физическая химия. Ч. 1, Отв. Редактор В. В. Лунин. МГУ химфак, 2002.
2. Рекомендуемая литература (основная) 1. А. Г. Стромберг, Д. П. Семченко. Физическая химия. М. : Высшая школа, 2007 . 523 с. 2. Полторак О. М. Термодинамика в физической химии. М. : Высшая школа, 1991. 319 с. 3. В. Д. Ягодовский. Статистическая термодинамика в физической химии. М. : Бином, 2005. 494 с. 4. Физическая химия. Ч. 1, Отв. Редактор В. В. Лунин. МГУ химфак, 2002.
 3. Статистическая термодинамика 3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы 3. 2 Статистические ансамбли , Ω и Г- фазовые пространства при описании термодинамических систем 3. 3 Связь термодинамической вероятности и энтропии
3. Статистическая термодинамика 3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы 3. 2 Статистические ансамбли , Ω и Г- фазовые пространства при описании термодинамических систем 3. 3 Связь термодинамической вероятности и энтропии
 3. Статистическая термодинамика 3. 4 Молекулярная сумма по состояниям. Сумма по состояниям системы 3. 5 Алгоритм вывода суммы по состояниям для отдельных видов движения 3. 6 Связь термодинамических функций и параметров с суммой по состояниям 3. 7 Расчет термодинамических функций и параметров при использовании суммы по состояниям
3. Статистическая термодинамика 3. 4 Молекулярная сумма по состояниям. Сумма по состояниям системы 3. 5 Алгоритм вывода суммы по состояниям для отдельных видов движения 3. 6 Связь термодинамических функций и параметров с суммой по состояниям 3. 7 Расчет термодинамических функций и параметров при использовании суммы по состояниям
 3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы Статистическая термодинамика – это раздел статистической физики, рассматривающий термодинамические свойства макроскопических систем на основе свойств её частиц и законов их движения.
3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы Статистическая термодинамика – это раздел статистической физики, рассматривающий термодинамические свойства макроскопических систем на основе свойств её частиц и законов их движения.
 3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы Изучение статистической термодинамики и использование ее в физической химии необходимо по двум главным причинам – статистическая термодинамика дает глубокое истолкование феноменологических закономерностей и способствует более точному пониманию физического смысла этих закономерностей – статистическая термодинамика дает методы расчета термодинамических величин с использованием молекулярных постоянных
3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы Изучение статистической термодинамики и использование ее в физической химии необходимо по двум главным причинам – статистическая термодинамика дает глубокое истолкование феноменологических закономерностей и способствует более точному пониманию физического смысла этих закономерностей – статистическая термодинамика дает методы расчета термодинамических величин с использованием молекулярных постоянных
 3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы При макроскопическом подходе для характеристики состояния системы используется небольшое число переменных (температура, объем, давление, концентрация, число частиц), которые остаются постоянными, если система находится в равновесном состоянии.
3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы При макроскопическом подходе для характеристики состояния системы используется небольшое число переменных (температура, объем, давление, концентрация, число частиц), которые остаются постоянными, если система находится в равновесном состоянии.
 3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы При микроскопическом подходе (классическая и квантовая механика) учитываются координаты и импульсы каждой частицы в каждый момент времени, определяющие микросостояния системы. Микроскопические параметры не остаются постоянными, а изменяются во времени. Это означает, что данному макросостоянию соответствует большое число (бесконечно много) микросостояний.
3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы При микроскопическом подходе (классическая и квантовая механика) учитываются координаты и импульсы каждой частицы в каждый момент времени, определяющие микросостояния системы. Микроскопические параметры не остаются постоянными, а изменяются во времени. Это означает, что данному макросостоянию соответствует большое число (бесконечно много) микросостояний.
 3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы o Итак, макросостояние системы – это совокупность числовых значений макропараметров: Т, V, Р, с 1, с 2, с 3……. . сn) и т. д. Они характеризуют систему в целом или ее макроскопические части. Микросостояние – это определенная совокупность числовых значений координат (q)и импульсов(p=m. V) всех частиц, входящих в состав данной макроскопической системы в фиксированный момент времени.
3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы o Итак, макросостояние системы – это совокупность числовых значений макропараметров: Т, V, Р, с 1, с 2, с 3……. . сn) и т. д. Они характеризуют систему в целом или ее макроскопические части. Микросостояние – это определенная совокупность числовых значений координат (q)и импульсов(p=m. V) всех частиц, входящих в состав данной макроскопической системы в фиксированный момент времени.
 3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы o Для операций с подобным множеством вводят понятие фазового пространства или Г-пространства. o Расположение N молекул(каждая из m атомов) определяется 3 Nm координатами ядер; o движение молекул описывается 3 Nm компонентами скоростей или импульсов. o Совокупность значений 6 Nm динамических переменных в каждый момент времени точно определяет микросостояние системы и называется фазой.
3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы o Для операций с подобным множеством вводят понятие фазового пространства или Г-пространства. o Расположение N молекул(каждая из m атомов) определяется 3 Nm координатами ядер; o движение молекул описывается 3 Nm компонентами скоростей или импульсов. o Совокупность значений 6 Nm динамических переменных в каждый момент времени точно определяет микросостояние системы и называется фазой.
 3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы o В этом пространстве каждое микросостояние в любой момент однозначно определяется положением одной точки, а изменение во времени импульсов и координат всех молекул передается некоторой линией, которую называют фазовой траекторией.
3. 1 Макроскопический и микроскопический подходы при описании термодинамической системы o В этом пространстве каждое микросостояние в любой момент однозначно определяется положением одной точки, а изменение во времени импульсов и координат всех молекул передается некоторой линией, которую называют фазовой траекторией.
 3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o В квантовой механике состояние той же системы описывается с помощью 3 Nm квантовых чисел, однозначно характеризующих 3 Nm степеней свободы всех молекул.
3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o В квантовой механике состояние той же системы описывается с помощью 3 Nm квантовых чисел, однозначно характеризующих 3 Nm степеней свободы всех молекул.
 3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o Пространство квантовых чисел обычно обозначают как Ωпространство. Оно имеет вдвое меньшее число измерений, чем Гпространство, в соответствии с невозможностью одновременно точно определить импульс и координату частицы
3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o Пространство квантовых чисел обычно обозначают как Ωпространство. Оно имеет вдвое меньшее число измерений, чем Гпространство, в соответствии с невозможностью одновременно точно определить импульс и координату частицы
 3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o Квазиклассическое приближение отвечает принципу соответствия в квантовой механике. Оно позволяет поставить во взаимное соответствие классическое Гпространство и квантовое Ωпространство: Nf o ∆ Ω= ∆Г/N!h
3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o Квазиклассическое приближение отвечает принципу соответствия в квантовой механике. Оно позволяет поставить во взаимное соответствие классическое Гпространство и квантовое Ωпространство: Nf o ∆ Ω= ∆Г/N!h
 3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o Это дает возможность использовать классическую механику для описания поступательного и вращательного движения и наиболее просто согласовать результаты классического и квантовомеханического расчетов статистических величин
3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o Это дает возможность использовать классическую механику для описания поступательного и вращательного движения и наиболее просто согласовать результаты классического и квантовомеханического расчетов статистических величин
 3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o Чтобы в каждый момент времени t иметь возможность точно определить динамическое состояние системы – указать координаты и импульсы всех частиц, в молекулярной динамике уравнение движения частиц интегрируют. Тогда любое термодинамическое свойство системы F можно рассматривать как некоторую усредненную величину от «мгновенных» значений F для каждой фазы.
3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o Чтобы в каждый момент времени t иметь возможность точно определить динамическое состояние системы – указать координаты и импульсы всех частиц, в молекулярной динамике уравнение движения частиц интегрируют. Тогда любое термодинамическое свойство системы F можно рассматривать как некоторую усредненную величину от «мгновенных» значений F для каждой фазы.
 3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли Эту величину называют средним по времени значением F : Здесь – время нахождения системы в окрестностях точки Г-пространства, определяющие все динамические параметры системы
3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли Эту величину называют средним по времени значением F : Здесь – время нахождения системы в окрестностях точки Г-пространства, определяющие все динамические параметры системы
 3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли где – вероятность того, что наугад выбранная система попадет в бесконечно малую область Г-пространства в окрестности данной точки (p, q). o Средние значения F можно вычислить, если будет найден общий вид функции . Это было сделано методами статистической механики
3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли где – вероятность того, что наугад выбранная система попадет в бесконечно малую область Г-пространства в окрестности данной точки (p, q). o Средние значения F можно вычислить, если будет найден общий вид функции . Это было сделано методами статистической механики
 3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o Ансамбли Гиббса – равновесные распределения вероятностей пребывания систем, состоящих из большого числа частиц в состояниях, реализуемых в различных физических условиях. o В принципе можно определить столько различных ансамблей, сколько существует способов контакта макроскопической системы с окружающей средой. Наибольшее значение приобрели три: микроканонический, канонический и большой канонический ансамбли.
3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o Ансамбли Гиббса – равновесные распределения вероятностей пребывания систем, состоящих из большого числа частиц в состояниях, реализуемых в различных физических условиях. o В принципе можно определить столько различных ансамблей, сколько существует способов контакта макроскопической системы с окружающей средой. Наибольшее значение приобрели три: микроканонический, канонический и большой канонический ансамбли.
 3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o Микроканонический ансамбль – это совокупность М→∞ изолированных систем с постоянными значениями энергии, объема и числа частиц. Сокращенно обозначаются (U, V, N). o Канонический ансамбль – совокупность М→∞ систем заданного объема, способных обмениваться энергией с окружающей средой и находящихся с ней в термодинамическом равновесии. Для них постоянны температура, объем системы и число частиц. Обозначаются (T, V, N). o Большой канонический ансамбль – совокупность М→∞ систем, способных обмениваться между собой энергией и частицами, т. е. систем, находящихся при постоянных температуре и химическом потенциале. Обозначим такой ансамбль (T, V, μ).
3. 2 Г и Ω - фазовые пространства при описании термодинамических систем, статистические ансамбли o Микроканонический ансамбль – это совокупность М→∞ изолированных систем с постоянными значениями энергии, объема и числа частиц. Сокращенно обозначаются (U, V, N). o Канонический ансамбль – совокупность М→∞ систем заданного объема, способных обмениваться энергией с окружающей средой и находящихся с ней в термодинамическом равновесии. Для них постоянны температура, объем системы и число частиц. Обозначаются (T, V, N). o Большой канонический ансамбль – совокупность М→∞ систем, способных обмениваться между собой энергией и частицами, т. е. систем, находящихся при постоянных температуре и химическом потенциале. Обозначим такой ансамбль (T, V, μ).
 3. 2 Обоснования усреднения по ансамблю в статистической термодинамике. o С помощью этих трех ансамблей задаются сразу все микросостояния интересующих нас термодинамических объектов. Чтобы усреднение по ансамблю можно было корректно использовать в термодинамике, статистическая физика использует три постулата.
3. 2 Обоснования усреднения по ансамблю в статистической термодинамике. o С помощью этих трех ансамблей задаются сразу все микросостояния интересующих нас термодинамических объектов. Чтобы усреднение по ансамблю можно было корректно использовать в термодинамике, статистическая физика использует три постулата.
 Обоснования усреднения по ансамблю в статистической термодинамике o Постулат эргоидности, необходимый для обоснования статистического метода расчета средних значений с помощью чуждого классической механике понятия о вероятности различных состояний в Гпространстве, и математической формулой которого будет приближение o .
Обоснования усреднения по ансамблю в статистической термодинамике o Постулат эргоидности, необходимый для обоснования статистического метода расчета средних значений с помощью чуждого классической механике понятия о вероятности различных состояний в Гпространстве, и математической формулой которого будет приближение o .
 Обоснования усреднения по ансамблю в статистической термодинамике o Постулат равных априорных вероятностей. Этот постулат позволяет использовать объем фазового пространства d. Г как меру множества равновероятных микросостояний и в общем случае искать вероятность o в виде
Обоснования усреднения по ансамблю в статистической термодинамике o Постулат равных априорных вероятностей. Этот постулат позволяет использовать объем фазового пространства d. Г как меру множества равновероятных микросостояний и в общем случае искать вероятность o в виде
 Обоснования усреднения по ансамблю в статистической термодинамике o где – плотность вероятности в Гпространстве o Из квантовой теории , где – постоянная Планка, – число степеней свободы одной частицы. Множитель учитывает неразличимость элементарных частиц системы. o Тогда для среднего по ансамблю можно написать соотношение o
Обоснования усреднения по ансамблю в статистической термодинамике o где – плотность вероятности в Гпространстве o Из квантовой теории , где – постоянная Планка, – число степеней свободы одной частицы. Множитель учитывает неразличимость элементарных частиц системы. o Тогда для среднего по ансамблю можно написать соотношение o
 Обоснования усреднения по ансамблю в статистической термодинамике Постулат о равновесной функции распределения. Равновесная функция в фазовом пространстве одновременно является и наиболее вероятной. Важнейшим её свойством является то, что она оказалась не чувствительной для равновесных систем к изменениям импульсов и координат отдельных молекул при движении системы по фазовой траектории. Это позволило разработать статистический метод определения термодинамических величин для равновесных систем.
Обоснования усреднения по ансамблю в статистической термодинамике Постулат о равновесной функции распределения. Равновесная функция в фазовом пространстве одновременно является и наиболее вероятной. Важнейшим её свойством является то, что она оказалась не чувствительной для равновесных систем к изменениям импульсов и координат отдельных молекул при движении системы по фазовой траектории. Это позволило разработать статистический метод определения термодинамических величин для равновесных систем.
 Обоснования усреднения по ансамблю в статистической термодинамике Для нахождения вида функции распределения используется теорема Лиувиля, доказательство которой означает, что плотность вероятности является постоянной величиной вдоль фазовых траекторий и не зависит от непрерывно изменяющихся значений импульсов и координат, если последние изменяются в соответствии с уравнениями движения.
Обоснования усреднения по ансамблю в статистической термодинамике Для нахождения вида функции распределения используется теорема Лиувиля, доказательство которой означает, что плотность вероятности является постоянной величиной вдоль фазовых траекторий и не зависит от непрерывно изменяющихся значений импульсов и координат, если последние изменяются в соответствии с уравнениями движения.
 Обоснования усреднения по ансамблю в статистической термодинамике o Однако, сказанное относится только к некоторым функциям от импульсов и координат, которые называют интегралами движения. В их числе находятся и 7 важнейших аддитивных интегралов движения классической механики: энергия, три компоненты вектора количества движения и три компоненты момента количества движения.
Обоснования усреднения по ансамблю в статистической термодинамике o Однако, сказанное относится только к некоторым функциям от импульсов и координат, которые называют интегралами движения. В их числе находятся и 7 важнейших аддитивных интегралов движения классической механики: энергия, три компоненты вектора количества движения и три компоненты момента количества движения.
 Обоснования усреднения по ансамблю в статистической термодинамике o Важнейшим из таких интегралов является энергия. Поэтому, в действительности, зависит не от координат и импульсов, отдельных частиц, а только от энергии системы. o Численное значение Z может быть найдено из условия нормировки имеет значение o
Обоснования усреднения по ансамблю в статистической термодинамике o Важнейшим из таких интегралов является энергия. Поэтому, в действительности, зависит не от координат и импульсов, отдельных частиц, а только от энергии системы. o Численное значение Z может быть найдено из условия нормировки имеет значение o
 Общие представления о сумме по состояниям o Величину Z называют интегралом состояний или суммой по состояниям. Ее определение представляет собой фактически первый шаг в переходе от предельного детализированного представления свойств молекулярной системы к обобщенному статистическому описанию.
Общие представления о сумме по состояниям o Величину Z называют интегралом состояний или суммой по состояниям. Ее определение представляет собой фактически первый шаг в переходе от предельного детализированного представления свойств молекулярной системы к обобщенному статистическому описанию.
 Общие представления о сумме по состояниям o При этом можно перейти от интегрирования по импульсам и координатам к интегрированию по энергиям. Для любой заданной молекулярной модели системы эти величины связаны однозначно между собой: o где – плотность состояний по энергии
Общие представления о сумме по состояниям o При этом можно перейти от интегрирования по импульсам и координатам к интегрированию по энергиям. Для любой заданной молекулярной модели системы эти величины связаны однозначно между собой: o где – плотность состояний по энергии
 Общие представления о сумме по состояниям Тогда для
Общие представления о сумме по состояниям Тогда для
 Общие представления о сумме по состояниям Если энергия изменяется не непрерывно, а принимает дискретные значения сумма по состояниям Z запишется в виде , где – число микросостояний системы, отвечающее данному значению
Общие представления о сумме по состояниям Если энергия изменяется не непрерывно, а принимает дискретные значения сумма по состояниям Z запишется в виде , где – число микросостояний системы, отвечающее данному значению
 Различные виды функции распределения Вид функции распределения можно найти несколькими способами. Есть три класса систем, соответствующих трем различным способам заполнения уровней энергии Г-пространства. В результате этого появляются три различные функции распределения: Максвелла. Больцмана, Бозе-Эйнштейна, Ферми. Дирака.
Различные виды функции распределения Вид функции распределения можно найти несколькими способами. Есть три класса систем, соответствующих трем различным способам заполнения уровней энергии Г-пространства. В результате этого появляются три различные функции распределения: Максвелла. Больцмана, Бозе-Эйнштейна, Ферми. Дирака.
 Различные виды функции распределения Статистический метод здесь один, а отличия связаны только с различной природой изучаемых систем. Они различаются по трем основным признакам: o по различимости или неразличимости изучаемых систем o по различимости ячеек фазового пространства, отвечающих данному значению энергии o по наличию ограничений, налагаемых на заполнение отдельных ячеек данного уровня энергии
Различные виды функции распределения Статистический метод здесь один, а отличия связаны только с различной природой изучаемых систем. Они различаются по трем основным признакам: o по различимости или неразличимости изучаемых систем o по различимости ячеек фазового пространства, отвечающих данному значению энергии o по наличию ограничений, налагаемых на заполнение отдельных ячеек данного уровня энергии
 Различные виды функции распределения o Статистика Максвелла-Больцмана: частицы различимы, нет принципиальных ограничений заполнения отдельных ячеек фазового пространства o Статистика Бозе-Эйнштейна: элементарные частицы неразличимы, в каждой из ячеек фазового пространства можно разместить любое число частиц, однако сами ячейки, как и частицы неразличимы. o Статистика Ферми-Дирака: частицы неразличимы, но каждую из неразличимых ячеек, принадлежащих определенному уровню энергии, может занимать не больше одной частицы.
Различные виды функции распределения o Статистика Максвелла-Больцмана: частицы различимы, нет принципиальных ограничений заполнения отдельных ячеек фазового пространства o Статистика Бозе-Эйнштейна: элементарные частицы неразличимы, в каждой из ячеек фазового пространства можно разместить любое число частиц, однако сами ячейки, как и частицы неразличимы. o Статистика Ферми-Дирака: частицы неразличимы, но каждую из неразличимых ячеек, принадлежащих определенному уровню энергии, может занимать не больше одной частицы.
 3. 3 Статистика Максвелла-Больцмана Остановимся на статистике Максвелла. Больцмана, согласно которой: 1. Все размещения в фазовом пространстве равновероятны 2. Данное распределение молекул по фазовым ячейкам образует данное микросостояние 3. Перемещение молекул внутри ячейки не образует нового микросостояния 4. Перестановка двух молекул в двух ячейках соответствует новому микросостоянию.
3. 3 Статистика Максвелла-Больцмана Остановимся на статистике Максвелла. Больцмана, согласно которой: 1. Все размещения в фазовом пространстве равновероятны 2. Данное распределение молекул по фазовым ячейкам образует данное микросостояние 3. Перемещение молекул внутри ячейки не образует нового микросостояния 4. Перестановка двух молекул в двух ячейках соответствует новому микросостоянию.
 3. 3. 1 Термодинамическая вероятность и ее связь с энтропией o Число микросостояний, отвечающих данному макросостоянию, определяется термодинамической вероятностью распределения молекул по ячейкам и выражается формулой o , где – общее число молекул системы, – число молекул в ячейках 1, 2, 3. . n.
3. 3. 1 Термодинамическая вероятность и ее связь с энтропией o Число микросостояний, отвечающих данному макросостоянию, определяется термодинамической вероятностью распределения молекул по ячейкам и выражается формулой o , где – общее число молекул системы, – число молекул в ячейках 1, 2, 3. . n.
 3. 3. 1 Термодинамическая вероятность и ее связь с энтропией При равномерном распределении частиц по ячейкам наибольшая термодинамическая вероятность равна
3. 3. 1 Термодинамическая вероятность и ее связь с энтропией При равномерном распределении частиц по ячейкам наибольшая термодинамическая вероятность равна
 3. 3. 1 Термодинамическая вероятность и ее связь с энтропией o В статистической термодинамике постулируется, что каждая представленная самой себе изолированная система стремится перейти в наиболее вероятное состояние, при этом термодинамическая вероятность изолированной системы приближается к максимуму. Таким образом, максимуму термодинамической вероятности соответствует равновесное состояние системы.
3. 3. 1 Термодинамическая вероятность и ее связь с энтропией o В статистической термодинамике постулируется, что каждая представленная самой себе изолированная система стремится перейти в наиболее вероятное состояние, при этом термодинамическая вероятность изолированной системы приближается к максимуму. Таким образом, максимуму термодинамической вероятности соответствует равновесное состояние системы.
 3. 3. 1 Термодинамическая вероятность и ее связь с энтропией o Для необратимых процессов, протекающих в изолированной системе, энтропия и термодинамическая вероятность растут и достигают максимального значения при установлении в системе равновесного состояния. Зависимость между энтропией и термодинамической вероятностью Больцман выразил уравнением o здесь – постоянная Больцмана, .
3. 3. 1 Термодинамическая вероятность и ее связь с энтропией o Для необратимых процессов, протекающих в изолированной системе, энтропия и термодинамическая вероятность растут и достигают максимального значения при установлении в системе равновесного состояния. Зависимость между энтропией и термодинамической вероятностью Больцман выразил уравнением o здесь – постоянная Больцмана, .
 3. 3. 1 Термодинамическая вероятность и ее связь с энтропией o Так как уравнение Больцмана связывает основную функцию второго закона термодинамики с основной величиной статистической термодинамики – термодинамической вероятностью, то оно объясняет статистический характер второго закона термодинамики и представляет его как следствие постулатов статистической термодинамики.
3. 3. 1 Термодинамическая вероятность и ее связь с энтропией o Так как уравнение Больцмана связывает основную функцию второго закона термодинамики с основной величиной статистической термодинамики – термодинамической вероятностью, то оно объясняет статистический характер второго закона термодинамики и представляет его как следствие постулатов статистической термодинамики.
 3. 3. 1 Термодинамическая вероятность и ее связь с энтропией o Из уравнения Больцмана вытекает статистическое толкование энтропии, определение которой в феноменологической термодинамике весьма формально и достаточно бедно по содержанию. Статистическое определение энтропии обладает тем преимуществом, что оно позволяет установить причину появления тех или иных свойств энтропии и дать им истолкование в молекулярной теории.
3. 3. 1 Термодинамическая вероятность и ее связь с энтропией o Из уравнения Больцмана вытекает статистическое толкование энтропии, определение которой в феноменологической термодинамике весьма формально и достаточно бедно по содержанию. Статистическое определение энтропии обладает тем преимуществом, что оно позволяет установить причину появления тех или иных свойств энтропии и дать им истолкование в молекулярной теории.
 3. 3. 1 Термодинамическая вероятность и ее связь с энтропией o Так, утверждение означает, что при абсолютном нуле все молекулы находятся в невозбужденном энергетическом состоянии. Если система однокомпонентная и отсутствует деформация кристаллической решетки, то молекулы неразличимы ни качественно, ни по энергиям.
3. 3. 1 Термодинамическая вероятность и ее связь с энтропией o Так, утверждение означает, что при абсолютном нуле все молекулы находятся в невозбужденном энергетическом состоянии. Если система однокомпонентная и отсутствует деформация кристаллической решетки, то молекулы неразличимы ни качественно, ни по энергиям.
 3. 3. 1 Термодинамическая вероятность и ее связь с энтропией Термодинамическая вероятность такой системы равна единице: . В соответствии с уравнением Больцмана энтропия такой системы равна нулю. Согласно постулату Планка энтропия правильно образованного кристалла при абсолютном нуле равна нулю.
3. 3. 1 Термодинамическая вероятность и ее связь с энтропией Термодинамическая вероятность такой системы равна единице: . В соответствии с уравнением Больцмана энтропия такой системы равна нулю. Согласно постулату Планка энтропия правильно образованного кристалла при абсолютном нуле равна нулю.
 Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы Закон распределения частиц идеального газа для равновесного состояния системы Молекулярная сумма по состояниям Степень вырождения (априорная вероятность) Сумма по состояниям системы
Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы Закон распределения частиц идеального газа для равновесного состояния системы Молекулярная сумма по состояниям Степень вырождения (априорная вероятность) Сумма по состояниям системы
 Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы o
Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы o
 Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы o
Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы o
 Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы o
Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы o
 Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы o
Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы o
 Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы 2. 1 2. 4 2. 2 2. 5 2. 3 2. 6
Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы 2. 1 2. 4 2. 2 2. 5 2. 3 2. 6
 Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы o Сумма по состояниям – это ключевое понятие для статистической оценки термодинамических свойств системы. Из него можно найти число частиц Ni, имеющих энергию εi. o Распределение частиц по уровням энергии называют распределением Больцмана, - больцмановским фактором
Распределение Больцмана. Молекулярная сумма по состояниям. Сумма по состояниям системы o Сумма по состояниям – это ключевое понятие для статистической оценки термодинамических свойств системы. Из него можно найти число частиц Ni, имеющих энергию εi. o Распределение частиц по уровням энергии называют распределением Больцмана, - больцмановским фактором
 Степень вырождения (априорная вероятность) o Термодинамическая вероятность и сумма по состояниям с учетом вырожденности 2. 7 2. 8 2. 9
Степень вырождения (априорная вероятность) o Термодинамическая вероятность и сумма по состояниям с учетом вырожденности 2. 7 2. 8 2. 9
 Свойства суммы по состояниям o Безразмерная величина o Зависит от молекулярной массы вещества o От температуры, объема o От характера движения молекул (момента инерции молекул, частоты собственных колебаний атомов в молекуле и др. )
Свойства суммы по состояниям o Безразмерная величина o Зависит от молекулярной массы вещества o От температуры, объема o От характера движения молекул (момента инерции молекул, частоты собственных колебаний атомов в молекуле и др. )
 Термодинамические функции и молекулярные суммы по состояниям o Сумма по состояниям для различных видов движения o Алгоритм расчета сумм по состояниям для различных видов движения o Выражение термодинамических параметров и функций через сумму по состояниям o Уравнения для расчета энтропии (разные виды движения)
Термодинамические функции и молекулярные суммы по состояниям o Сумма по состояниям для различных видов движения o Алгоритм расчета сумм по состояниям для различных видов движения o Выражение термодинамических параметров и функций через сумму по состояниям o Уравнения для расчета энтропии (разные виды движения)
 Сумма по состояниям для различных видов движения
Сумма по состояниям для различных видов движения
 Зависимость суммы по состояниям от молекулярных констант и параметров состояния системы o Поступательная сумма по состояниям
Зависимость суммы по состояниям от молекулярных констант и параметров состояния системы o Поступательная сумма по состояниям
 Зависимость суммы по состояниям от молекулярных констант и параметров состояния системы o Поступательная сумма по состояниям
Зависимость суммы по состояниям от молекулярных констант и параметров состояния системы o Поступательная сумма по состояниям
 Зависимость суммы по состояниям от молекулярных констант и параметров состояния системы o Поступательная сумма по состояниям
Зависимость суммы по состояниям от молекулярных констант и параметров состояния системы o Поступательная сумма по состояниям
 Зависимость суммы по состояниям от молекулярных констант и параметров состояния системы o Сумма по состояниям, обусловленная электронным движением в молекулах
Зависимость суммы по состояниям от молекулярных констант и параметров состояния системы o Сумма по состояниям, обусловленная электронным движением в молекулах
 Зависимость суммы по состояниям от молекулярных констант и параметров состояния системы
Зависимость суммы по состояниям от молекулярных констант и параметров состояния системы
 Сумма по состояниям, обусловленная вращательным движением в молекулах
Сумма по состояниям, обусловленная вращательным движением в молекулах
 Сумма по состояниям, обусловленная вращательным движением в молекулах
Сумма по состояниям, обусловленная вращательным движением в молекулах
 Сумма по состояниям, обусловленная колебательным движением в молекулах Колебательное движение двухатомной молекулы рассматривается как движение гармонического осциллятора, энергия которого определяется по уравнению
Сумма по состояниям, обусловленная колебательным движением в молекулах Колебательное движение двухатомной молекулы рассматривается как движение гармонического осциллятора, энергия которого определяется по уравнению
 Сумма по состояниям, обусловленная колебательным движением в молекулах
Сумма по состояниям, обусловленная колебательным движением в молекулах
 Выражения для сумм по состояниям в логарифмической форме
Выражения для сумм по состояниям в логарифмической форме
 Алгоритм расчета суммы по состояниям (поступательная составляющая) (3. 1)
Алгоритм расчета суммы по состояниям (поступательная составляющая) (3. 1)
 Алгоритм расчета суммы по состояниям (электронная составляющая) (3. 2) (3. 1)+(3. 2) (3. 3)
Алгоритм расчета суммы по состояниям (электронная составляющая) (3. 2) (3. 1)+(3. 2) (3. 3)
 Алгоритм расчета суммы по состояниям (вращательная составляющая) (3. 4)
Алгоритм расчета суммы по состояниям (вращательная составляющая) (3. 4)
 Алгоритм расчета суммы по состояниям (колебательная составляющая) (3. 5)
Алгоритм расчета суммы по состояниям (колебательная составляющая) (3. 5)
 Выражение термодинамических параметров и функций через сумму по состояниям o Практической целью статистической термодинамики является вычисление термодинамических величин по молекулярным данным. Микроскопические свойства частиц макроскопической системы заложены в параметре, который мы с вами вывели на предыдущих лекциях – молекулярной сумме по состояниям (Q).
Выражение термодинамических параметров и функций через сумму по состояниям o Практической целью статистической термодинамики является вычисление термодинамических величин по молекулярным данным. Микроскопические свойства частиц макроскопической системы заложены в параметре, который мы с вами вывели на предыдущих лекциях – молекулярной сумме по состояниям (Q).
 Выражение термодинамических параметров и функций через сумму по состояниям o Для произведения расчетов термодинамических функций, параметров необходимо найти связь между двумя этими величинами. o Получим выражения для ряда термодинамических функций одного моля газа через суммы по состояниям
Выражение термодинамических параметров и функций через сумму по состояниям o Для произведения расчетов термодинамических функций, параметров необходимо найти связь между двумя этими величинами. o Получим выражения для ряда термодинамических функций одного моля газа через суммы по состояниям
 Выражение термодинамических параметров и функций через сумму по состояниям o
Выражение термодинамических параметров и функций через сумму по состояниям o
 Выражение термодинамических параметров и функций через сумму по состояниям o
Выражение термодинамических параметров и функций через сумму по состояниям o
 Выражение термодинамических параметров и функций через сумму по состояниям o
Выражение термодинамических параметров и функций через сумму по состояниям o
 Выражение термодинамических параметров и функций через сумму по состояниям o
Выражение термодинамических параметров и функций через сумму по состояниям o
 Выражение термодинамических параметров и функций через сумму по состояниям o
Выражение термодинамических параметров и функций через сумму по состояниям o
 Связь термодинамических функций и параметров с суммой по состояниям
Связь термодинамических функций и параметров с суммой по состояниям
 Уравнения для расчета энтропии (разные виды движения) (3. 6) (3. 7) (3. 8)
Уравнения для расчета энтропии (разные виды движения) (3. 6) (3. 7) (3. 8)
 Примеры решения задач по статистической термодинамике Задача 1 1. Молекула может находиться на уровне с энергией 0 (условное обозначение) или на одном из 3 -х уровней с энергией Е. Чему равна молекулярная сумма по состояниям? При какой температуре: а) все молекулы будут находиться на нижнем уровне б) число молекул на нижнем уровне будет равно числу молекул на верхних уровнях в) число молекул на нижнем уровне будет в три раза меньше, чем число молекул на верхних уровнях?
Примеры решения задач по статистической термодинамике Задача 1 1. Молекула может находиться на уровне с энергией 0 (условное обозначение) или на одном из 3 -х уровней с энергией Е. Чему равна молекулярная сумма по состояниям? При какой температуре: а) все молекулы будут находиться на нижнем уровне б) число молекул на нижнем уровне будет равно числу молекул на верхних уровнях в) число молекул на нижнем уровне будет в три раза меньше, чем число молекул на верхних уровнях?
 Решение задачи № 1 o Решение Распределение частиц по уровням энергии описывается распределением Больцмана (4. 5): где Ni – число частиц на i-том уровне с энергией i, N – общее число частиц. В соответствии с условиями задачи распределение Больцмана может быть представлено в виде .
Решение задачи № 1 o Решение Распределение частиц по уровням энергии описывается распределением Больцмана (4. 5): где Ni – число частиц на i-том уровне с энергией i, N – общее число частиц. В соответствии с условиями задачи распределение Больцмана может быть представлено в виде .
 Решение задачи № 1 Молекулярная сумма по состояниям а) При понижении температуры накапливаются на нижних уровнях. молекулы
Решение задачи № 1 Молекулярная сумма по состояниям а) При понижении температуры накапливаются на нижних уровнях. молекулы
 Решение задачи № 1 б). В) При высоких температурах молекулы равномерно распределены по уровням энергии, т. к. все больцмановские множители почти одинаковы и равны 1.
Решение задачи № 1 б). В) При высоких температурах молекулы равномерно распределены по уровням энергии, т. к. все больцмановские множители почти одинаковы и равны 1.
 Примеры решения задач по статистической термодинамике o Задача 2 Молекула может находиться на двух уровнях с энергиями 0 и 300 см-1. Какова вероятность того, что молекула будет находиться на верхнем уровне при 2500 о. С?
Примеры решения задач по статистической термодинамике o Задача 2 Молекула может находиться на двух уровнях с энергиями 0 и 300 см-1. Какова вероятность того, что молекула будет находиться на верхнем уровне при 2500 о. С?
 Решение задачи № 2 o Применяем распределение Больцмана. Но для этого необходимо перевести спектроскопические единицы энергии см -1 в джоули, используя множитель hc. h=6. 63∙ 10 -34 Дж∙с; с=3∙ 1010 см/с; o 300 см-1=300∙ 6. 63∙ 10 -34∙ 3∙ 1010= 5. 97∙ 10 -21 Дж. o
Решение задачи № 2 o Применяем распределение Больцмана. Но для этого необходимо перевести спектроскопические единицы энергии см -1 в джоули, используя множитель hc. h=6. 63∙ 10 -34 Дж∙с; с=3∙ 1010 см/с; o 300 см-1=300∙ 6. 63∙ 10 -34∙ 3∙ 1010= 5. 97∙ 10 -21 Дж. o
 Решение задачи № 2
Решение задачи № 2
 Примеры решения задач по статистической термодинамике o Задача 3 1. Определите поступательную составляющую суммы состояний СО при 1, 0133∙ 105 Па и 500 К.
Примеры решения задач по статистической термодинамике o Задача 3 1. Определите поступательную составляющую суммы состояний СО при 1, 0133∙ 105 Па и 500 К.
 Решение задачи № 3 o После подстановки молекулярной массы, давления и температуры в уравнение (6. 1) получим o ln Qпост = 3, 4539 lg 28 + 5, 7565 lg 500 – 2, 23026 lg 1, 0133∙ 105 + 8, 8612 = o = 4, 9983 + 15, 5365 – 11, 5262 + 8, 8612 = 17, 8669, o lg Qпост = 7, 7607, Qпост = 5, 764∙ 107.
Решение задачи № 3 o После подстановки молекулярной массы, давления и температуры в уравнение (6. 1) получим o ln Qпост = 3, 4539 lg 28 + 5, 7565 lg 500 – 2, 23026 lg 1, 0133∙ 105 + 8, 8612 = o = 4, 9983 + 15, 5365 – 11, 5262 + 8, 8612 = 17, 8669, o lg Qпост = 7, 7607, Qпост = 5, 764∙ 107.
 Примеры решения задач по статистической термодинамике o Задача 4 1. Определите вращательную составляющую суммы состояний СО при 500 К. Момент инерции СО равен 14, 49∙ 10 – 47 кг∙м 2.
Примеры решения задач по статистической термодинамике o Задача 4 1. Определите вращательную составляющую суммы состояний СО при 500 К. Момент инерции СО равен 14, 49∙ 10 – 47 кг∙м 2.
 Решение задачи № 4 o Вращательную составляющую суммы состояний определим по уравнению (6. 4). Молекула СО гетероядерная, следовательно, σ = 1: o ln Qвр = 2, 3026 lg 14, 49∙ 10 – 47 + 2, 3026 lg 500 – 2, 3026 lg 1 + 104, 5265 = o = – 105, 5487 – 6, 2146 + 104, 5265 = 5, 1924, o lg Qвр = 2, 2550, Qвр = 179, 9.
Решение задачи № 4 o Вращательную составляющую суммы состояний определим по уравнению (6. 4). Молекула СО гетероядерная, следовательно, σ = 1: o ln Qвр = 2, 3026 lg 14, 49∙ 10 – 47 + 2, 3026 lg 500 – 2, 3026 lg 1 + 104, 5265 = o = – 105, 5487 – 6, 2146 + 104, 5265 = 5, 1924, o lg Qвр = 2, 2550, Qвр = 179, 9.
 Примеры решения задач по статистической термодинамике o Задача 5. o Определите колебательную суммы состояний СО при 500 К, если частота колебательного движения составляет 2, 170∙ 105 м – 1.
Примеры решения задач по статистической термодинамике o Задача 5. o Определите колебательную суммы состояний СО при 500 К, если частота колебательного движения составляет 2, 170∙ 105 м – 1.
 Рещение задачи № 5 o Определим характеристическую температуру по уравнению (6. 5): o = 1, 4387∙ 10 – 2 ∙ 2, 170∙ 105 = 3123, o = o Колебательную составляющую суммы состояний вычислим по уравнению (6. 5): o Qкол = .
Рещение задачи № 5 o Определим характеристическую температуру по уравнению (6. 5): o = 1, 4387∙ 10 – 2 ∙ 2, 170∙ 105 = 3123, o = o Колебательную составляющую суммы состояний вычислим по уравнению (6. 5): o Qкол = .
 Примеры решения задач по статистической термодинамике o Задача 6. o Вычислить общую сумму по состояниям Q для СО при р=1. 013∙ 105 Па и 500 К
Примеры решения задач по статистической термодинамике o Задача 6. o Вычислить общую сумму по состояниям Q для СО при р=1. 013∙ 105 Па и 500 К
 Решение задачи № 6 o Общую сумму по состояниям Q вычисляем по уравнению 1. Поступательную составляющую Qn находим из уравнения lg. Qn= 1. 5 lg. M + 2. 5 lg. T – lg. P + 0. 434∙ 19. 25 Для СО М=28∙ 10 -3 кг/моль lg. Qn= 1. 5 lg 28∙ 10 -3 + 2. 5 lg 500 – lg 1. 013∙ 105+8. 36=7. 76 Qn = 5. 77∙ 107
Решение задачи № 6 o Общую сумму по состояниям Q вычисляем по уравнению 1. Поступательную составляющую Qn находим из уравнения lg. Qn= 1. 5 lg. M + 2. 5 lg. T – lg. P + 0. 434∙ 19. 25 Для СО М=28∙ 10 -3 кг/моль lg. Qn= 1. 5 lg 28∙ 10 -3 + 2. 5 lg 500 – lg 1. 013∙ 105+8. 36=7. 76 Qn = 5. 77∙ 107
 Решение задачи № 6 2. Вращательную составляющую Qв находим по уравнению Так как молекула СО является несимметричной двухатомной молекулой. По справочнику находим момент инерции вращения молекулы I=14. 5∙ 10 -47 кг ∙м 2 и тогда вычисление даст Qв = 180.
Решение задачи № 6 2. Вращательную составляющую Qв находим по уравнению Так как молекула СО является несимметричной двухатомной молекулой. По справочнику находим момент инерции вращения молекулы I=14. 5∙ 10 -47 кг ∙м 2 и тогда вычисление даст Qв = 180.
 _ Решение задачи № 6 o 3. Колебательную составляющую Qk находим по уравнению Характеристическая температура определяется по уравнению где частота колебаний атомов в молекуле СО. В свою очередь с – скорость света, - волновое число собственных колебаний. По справочнику для СО =2. 170∙ 105 м-1
_ Решение задачи № 6 o 3. Колебательную составляющую Qk находим по уравнению Характеристическая температура определяется по уравнению где частота колебаний атомов в молекуле СО. В свою очередь с – скорость света, - волновое число собственных колебаний. По справочнику для СО =2. 170∙ 105 м-1
 Решение задачи № 6 Находим θ Для Т=500 К θ/500 = 6. 24 4. Электронную составляющую Qэ находим по уравнению Для СО q 0=1; Uоэ=0, поэтому Общая сумма по состояниям будет
Решение задачи № 6 Находим θ Для Т=500 К θ/500 = 6. 24 4. Электронную составляющую Qэ находим по уравнению Для СО q 0=1; Uоэ=0, поэтому Общая сумма по состояниям будет
 ВЫвод o Основной вклад в общую сумму по состояниям в данных условиях вносит поступательная составляющая, меньшую роль играет вращательная составляющая, и практически не сказывается на величине Q колебательные и электронные составляющие.
ВЫвод o Основной вклад в общую сумму по состояниям в данных условиях вносит поступательная составляющая, меньшую роль играет вращательная составляющая, и практически не сказывается на величине Q колебательные и электронные составляющие.
 Примеры решения задач по статистической термодинамике Задача 7. Вычислить абсолютную энтропию одного моля хлора при стандартных условиях 1. В соответствие с уравнением 6. 6 И учитывая, что для хлора g=1 имеем М=70. 91∙ 10 -3 кг/моль; T=298; р=1. 013∙ 105 Па, тогда Sпэ=161. 9 Дж/моль. К.
Примеры решения задач по статистической термодинамике Задача 7. Вычислить абсолютную энтропию одного моля хлора при стандартных условиях 1. В соответствие с уравнением 6. 6 И учитывая, что для хлора g=1 имеем М=70. 91∙ 10 -3 кг/моль; T=298; р=1. 013∙ 105 Па, тогда Sпэ=161. 9 Дж/моль. К.
 2. По уравнению находим Sв. Для молекулы хлора момент инерции I=113. 9∙ 10 -47 кг∙м 2, число симметрии σ=2 Sв = 8. 314(ln 298+ln 113. 9∙ 10 -47 – ln 2 + 105. 5) = 58. 34 Дж/моль∙К 3. По уравнению
2. По уравнению находим Sв. Для молекулы хлора момент инерции I=113. 9∙ 10 -47 кг∙м 2, число симметрии σ=2 Sв = 8. 314(ln 298+ln 113. 9∙ 10 -47 – ln 2 + 105. 5) = 58. 34 Дж/моль∙К 3. По уравнению
 вычисляем Sk. Для молекулы хлора характеристическая температура θ=812. 8; θ/298 = 2. 72 Sк=- 8. 314 ln(1 - 2. 718 -2. 72) +8. 3143∙ 2. 72/(2. 718+2. 72 1)=8. 314(-0. 0611)+8. 314 ∙ 0. 1941=2. 12 Дж/моль ∙К Таким образом, для моля хлора имеем So 298 = 161. 90 + 58. 34 +2. 12 = 222. 4 Дж/моль ∙К Справочные данные для энтропии Дж/моль ∙К
вычисляем Sk. Для молекулы хлора характеристическая температура θ=812. 8; θ/298 = 2. 72 Sк=- 8. 314 ln(1 - 2. 718 -2. 72) +8. 3143∙ 2. 72/(2. 718+2. 72 1)=8. 314(-0. 0611)+8. 314 ∙ 0. 1941=2. 12 Дж/моль ∙К Таким образом, для моля хлора имеем So 298 = 161. 90 + 58. 34 +2. 12 = 222. 4 Дж/моль ∙К Справочные данные для энтропии Дж/моль ∙К
 Примеры решения задач по статистической термодинамике o Задача 8. o Рассчитайте мольные энтропию, внутреннюю энергию, энтальпию, энергии Гельмгольца и Гиббса газообразного азота при Т = 298 К и давлении 1 атм. Вращательная постоянная В = 2. 00 см-1, колебательная частота ω = 2360 см-1. Электронной и ядерной составляющими пренебречь.
Примеры решения задач по статистической термодинамике o Задача 8. o Рассчитайте мольные энтропию, внутреннюю энергию, энтальпию, энергии Гельмгольца и Гиббса газообразного азота при Т = 298 К и давлении 1 атм. Вращательная постоянная В = 2. 00 см-1, колебательная частота ω = 2360 см-1. Электронной и ядерной составляющими пренебречь.
 Примеры решения задач по статистической термодинамике o Решение. Колебательным вкладом здесь можно пренебречь, т. к. температура Т = 298 К намного меньше эффективной колебательной температуры
Примеры решения задач по статистической термодинамике o Решение. Колебательным вкладом здесь можно пренебречь, т. к. температура Т = 298 К намного меньше эффективной колебательной температуры
 Примеры решения задач по статистической термодинамике o Рассчитаем поступательную и вращательную суммы по состояниям:
Примеры решения задач по статистической термодинамике o Рассчитаем поступательную и вращательную суммы по состояниям:
 Примеры решения задач по статистической термодинамике o Внутреннюю энергию можно найти по теореме о распределении по степеням свободы: o Мольную энтальпию можно найти – по определению H = U + p. V:
Примеры решения задач по статистической термодинамике o Внутреннюю энергию можно найти по теореме о распределении по степеням свободы: o Мольную энтальпию можно найти – по определению H = U + p. V:
 Примеры решения задач по статистической термодинамике o Мольную энтропию находим по формулам:
Примеры решения задач по статистической термодинамике o Мольную энтропию находим по формулам:
 Примеры решения задач по статистической термодинамике o а энергии Гельмгольца и Гиббса – по определению F = U – TS и G =F +p. V:
Примеры решения задач по статистической термодинамике o а энергии Гельмгольца и Гиббса – по определению F = U – TS и G =F +p. V:
 Суммы по состояниям для различных видов движения
Суммы по состояниям для различных видов движения
 Уважаемые студенты! o Это все надо выучить! o Главное, понять! o Желаю успеха!
Уважаемые студенты! o Это все надо выучить! o Главное, понять! o Желаю успеха!


