лектор Максина Александра Генриховна ТЕМАТИКА ЛЕКЦИЙ по

Скачать презентацию лектор Максина Александра Генриховна ТЕМАТИКА ЛЕКЦИЙ по

TV.pptx

Количество слайдов: 36

лектор Максина Александра Генриховна

ТЕМАТИКА ЛЕКЦИЙ по дисциплине «ФИЗИКА И МАТЕМАТИКА» ДЛЯ СТУДЕНТОВ 1 КУРСА ЛЕЧЕБНОГО И ПЕДИАТРИЧЕСКОГО ФАКУЛЬТЕТОВ НА 1 СЕМЕСТР 2015/2016 УЧ. ГОДА Тематика лекций 1 2 3 4 5 6 7 8 9 Теория вероятностей. Механические волны. Эффект Доплера Акустика. Течение и вязкость жидкостей. Физические основы гемодинамики. Физика биологических мембран. Биопотенциалы. Электрография органов и тканей. Электрические свойства биологических тканей.

1 СЕМЕСТР 2015/2016 УЧ. ГОДА 2 3 4 5 6 7 8 9 10 11 1. Высшая математика Математическая статистика 1 Модуль 2. Механические волны. Механические свойства тканей. Биологические мембраны Номер недели Тема 1. 1 1. 2 1. 3 1. 4 1. 5 1. 6 15 16 17 18 19 3. Электрические свойства тканей. 14 Элементы математического анализа № 2. Интегрирование функций. Решение дифференциальных уравнений. Контрольная работа № 1. Математическая статистика№ 1 Математическая статистика № 2 Математическая статистика № 3 Контрольная работа № 2 2. 1 Акустика. Лабораторная работа № 5. 2. 2 Физические основы применения ультразвука в медицине 2. 3 Механические свойства биологических тканей. Лабораторная работа № 11 2. 4 Течение и вязкость жидкостей. Лабораторные работы №№ 7, 8 2. 5 Биологические мембраны. Транспорт веществ через мембраны. Лабораторная работа № 14 12 13 Элементы математического анализа № 1. Производная функции. Дифференциал функции. 3. 1 3. 2 3. 3 3. 4 КОНТРОЛЬ ПО МОДУЛЮ 2 Электрическое поле. Проводники и диэлектрики в электрическом поле. Электрический диполь. Переменный ток. Импеданс цепи переменного тока. Лабораторная работа № 18 Электрические свойства биологических тканей. Лабораторная работа № 19 Физические основы электрокардиографии. Лабораторная работа № 27 КОНТРОЛЬ ПО МОДУЛЮ 3 ИТОГОВЫЙ КОНТРОЛЬ ПО КУРСУ Сдача лабораторных работ ЗАЧЕТ

Адрес электронного портала: http: //eois. rsmu. ru/med/ Дистанционно для студентов будет работать с 07 сентября 2014 года

МАТЕМАТИКА "ТЕОРИЯ ВЕРОЯТНОСТЕЙ" I. СЛУЧАЙНЫЕ СОБЫТИЯ. II. ВЕРОЯТНОСТЬ. III. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. РАСПРЕДЕЛЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И ЕГО ХАРАКТЕРИСТИКИ. IV. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН.

I. СЛУЧАЙНЫЕ СОБЫТИЯ. II. ВЕРОЯТНОСТЬ. III. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. РАСПРЕДЕЛЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И ЕГО ХАРАКТЕРИСТИКИ. IV. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН.

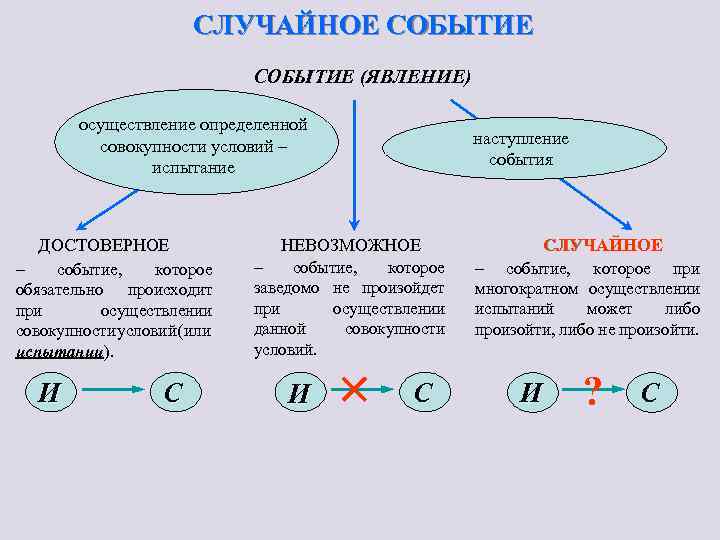СЛУЧАЙНОЕ СОБЫТИЕ (ЯВЛЕНИЕ) осуществление определенной совокупности условий – испытание ДОСТОВЕРНОЕ – событие, которое обязательно происходит при осуществлении совокупности условий (или испытании). И С наступление события НЕВОЗМОЖНОЕ – событие, которое заведомо не произойдет при осуществлении данной совокупности условий. И С СЛУЧАЙНОЕ – событие, которое при многократном осуществлении испытаний может либо произойти, либо не произойти. И ? С

ВЕРОЯТНОСТЬ – количественная характеристика степени возможности ВЕРОЯТНОСТЬ наступления события. статистическое определение вероятности n – число испытаний m – число появлений события А (число благоприятствующих испытаний) относительная частота события А классическое определение вероятности n – число равновозможных несовместных событий m – число благоприятствующих исходов событию А Вероятность равна отношению числа благоприятствующих исходов (m) к общему числу исходов (n)

или – число благоприятствующих испытаний – число благоприятствующих исходов СОБЫТИЕ ДОСТОВЕРНОЕ – событие, которое обязательно происходит при осуществлении совокупности условий (или испытании). И С НЕВОЗМОЖНОЕ – событие, которое заведомо не произойдет при осуществлении данной совокупности условий. С И СЛУЧАЙНОЕ – событие, которое при многократном осуществлении испытаний может либо произойти, либо не произойти. И ? С m=n m=0 0

ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ Вероятность появления одного из нескольких несовместных событий равна сумме их вероятностей. НЕСОВМЕСТНЫЕ СОБЫТИЯ (А) – события, которые ни при каких условиях не могут произойти вместе (на верхней грани игральной кости получить цифру 1 и 2) ПРОТОВОПОЛОЖНЫЕ СОБЫТИЯ ( ) – события, появление одного из которых исключает появление другого (появление четной и нечетной цифры на верхней грани игральной кости) Систему событий называют полной, если при любом испытании наступит одно из полной событий этой системы (выпадение цифр от 1 до 6 на верхней грани игральной кости) УСЛОВИЕ НОРМИРОВКИ: сумма вероятностей событий, образующих полную систему равна 1.

ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ Вероятность совместного появления независимых событий равна произведению их вероятностей. События называют НЕЗАВИСИМЫМИ, если наступление одного не зависит от наступления другого. Вероятность такого события меньше вероятности каждого отдельного события

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ СЛУЧАЙНАЯ ВЕЛИЧИНА (СВ) – величина, значение которой зависит от стечения случайных обстоятельств. число родившихся мальчиков среди ста новорожденных; расстояние, которое пролетит снаряд при выстреле из орудия; размер эритроцита; число заболевших гриппом; частота пульса пациента; температура тела. X, Y, Z – обозначение случайной величины, x, y, z – значения случайной величины. СЛУЧАЙНАЯ ВЕЛИЧИНА ДИСКРЕТНАЯ (ДСВ) СВ, которая принимает отдельные, изолированные значения (или счетное множество значений). НЕПРЕРЫВНАЯ (НСВ) СВ, которая может принимать все значения из некоторого промежутка.

ДИСКРЕТНАЯ СВ принимает отдельные, изолированные значения (или счетное множество значений). Распределение ДСВ представляет собой совокупность ее возможных значений и соответствующих им вероятностей. X x 1 x 2 … xk P p 1 p 2 … pk P УСЛОВИЕ НОРМИРОВКИ (x 2 , p 2) (x 4 , p 4) (x 1 , p 1) (x 3 , p 3) X МНОГОУГОЛЬНИК РАСПРЕДЕЛЕНИЯ

Величины, которые описывают случайную величину, называют ЧИСЛОВЫМИ ХАРАКТЕРИСТИКАМИ случайной величины. ü МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ случайной величины равно сумме произведений всех ее возможных значений и их вероятностей. X m Если x 1 x 2 … xk m 1 m 2 … mk , то

ü МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ Математическое ожидание примерно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины. M(X) xmin xmax X xmin < M(X) < xmax Математическое ожидание характеризует расположение распределения.

üДИСПЕРСИЯ случайной величины характеризует разброс случайных величин в данном распределении. По определению, дисперсия равна математическому ожиданию квадрата отклонения случайной величины от ее математического ожидания: Истинной мерой разброса случайной величины в данном распределении является СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ ü

НЕПРЕРЫВНАЯ СВ может принимать все значения из некоторого промежутка. НЕПРЕРЫВНАЯ Распределение НСВ задают функцией распределения вероятностей и функцией распределения непрерывной случайной величины. ü Функция плотности вероятности (плотность вероятности) – ширина интервала (промежуток) X – вероятность того, что НСВ принимает значения из этого интервала Плотность вероятности показывает, как изменяется вероятность, отнесенная к интервалу НСВ в зависимости от значения самой величины. Вероятность того, что СВ принимает какое-либо значение в интервале (a; b): УСЛОВИЕ НОРМИРОВКИ:

ü Функция распределения НСВ – функция, определяющая вероятность того, что СВ X примет значения, меньшие . a x’ b X 0 < F(x) < 1 ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ непрерывной случайной величины. ХАРАКТЕРИСТИКИ ü МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ü ДИСПЕРСИЯ ü СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ

ДСВ НСВ ОПРЕДЕЛЕНИЕ СВ, которая принимает СВ, которая может принимать все отдельные, изолированные значения из некоторого значения (или счетное промежутка. множество значений). РАСПРЕДЕЛЕНИЕ Совокупность возможных Плотность вероятности и значений и соответствующих им функция распределения вероятностей. непрерывной случайной величины. УСЛОВИЕ НОРМИРОВКИ МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДИСПЕРСИЯ СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ЗАКОН РАСПРЕДЕЛЕНИЯ – связь между плотностью вероятности и значением случайной величины. 1. Нормальное распределение (распределение Гаусса) Основные параметры нормального распределения: f(x) F(x) 1 a x 0 x

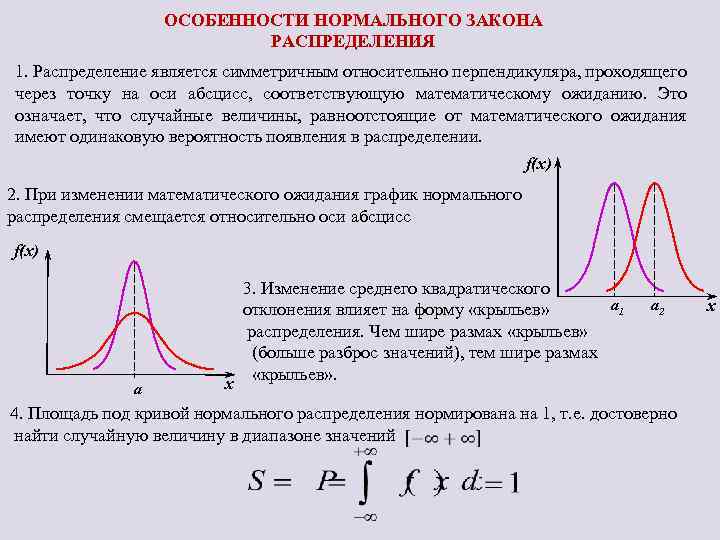ОСОБЕННОСТИ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ 1. Распределение является симметричным относительно перпендикуляра, проходящего через точку на оси абсцисс, соответствующую математическому ожиданию. Это означает, что случайные величины, равноотстоящие от математического ожидания имеют одинаковую вероятность появления в распределении. f(x) 2. При изменении математического ожидания график нормального распределения смещается относительно оси абсцисс f(x) a 3. Изменение среднего квадратического a 1 отклонения влияет на форму «крыльев» распределения. Чем шире размах «крыльев» (больше разброс значений), тем шире размах «крыльев» . x a 2 4. Площадь под кривой нормального распределения нормирована на 1, т. е. достоверно найти случайную величину в диапазоне значений x

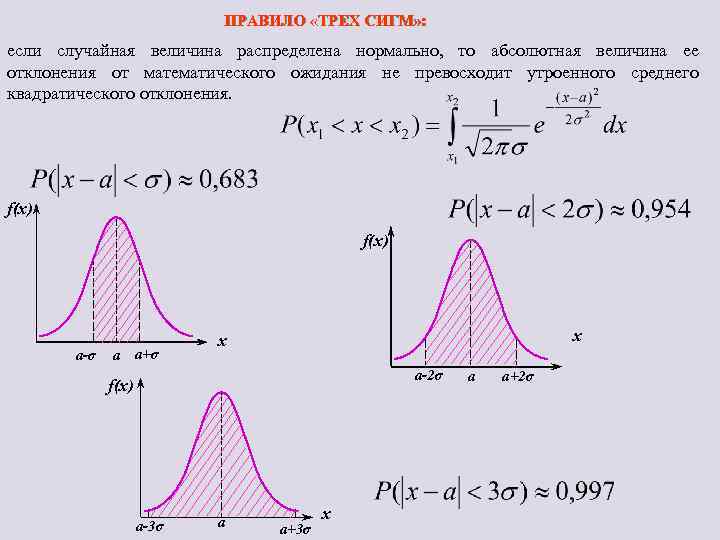ПРАВИЛО «ТРЕХ СИГМ» : если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. f(x) a-σ a a+σ x x a-2σ f(x) a-3σ a a+3σ x a a+2σ

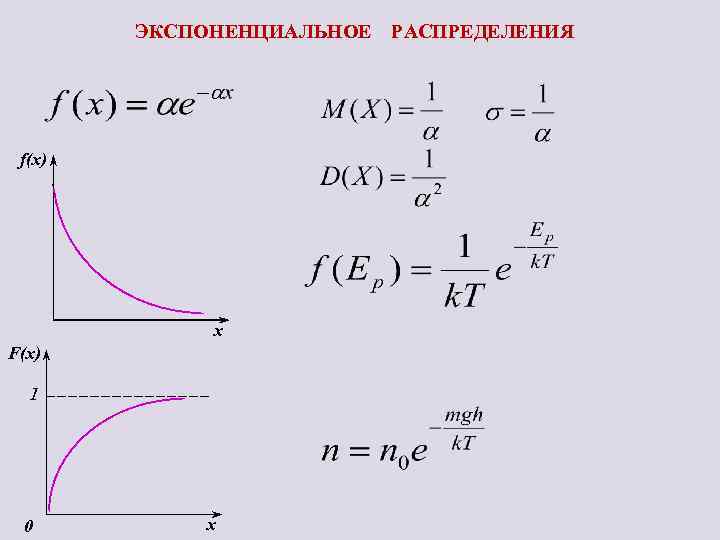ЭКСПОНЕНЦИАЛЬНОЕ f(x) x F(x) 1 0 x РАСПРЕДЕЛЕНИЯ

"МАТЕМАТИЧЕСКАЯ СТАТИСТИКА" – наука о математических методах систематизации и использования статистических данных для решения научных и практических задач. ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ: МАТЕМАТИЧЕСКАЯ СТАТИСТИКА üанализ статистических данных; üопределение вида распределения, которому соответствуют опытные данные; üсоставление прогнозов и проверка гипотез. Э. Резерфорд: «Если для вашего эксперимента нужна статистика, вам следовало бы провести его получше» В биологии и медицине сильно выражена изменчивость различных показателей. Поэтому идея описания популяции средними показателями очень популярна. Для выработки средних стандартов проводят исследования очень большого количества опытных данных

ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ – большая статистическая совокупность однородных элементов (объектов), обладающих общими признаками. не всегда доступны для исследования все объекты; подвижные совокупности; возможно потребуется уничтожение всех объектов при исследовании; большие временные и материальные затраты. ВЫБОРОЧНАЯ СОВОКУПНОСТЬ (ВЫБОРКА) – часть генеральной совокупности, объекты отобранные для исследования. Требования к выборке: ВЫБОРКА ü представительная (репрезентативная); ü случайная; ü достаточный объем. большая, n > 30 малая, n ≤ 30

ВЫБОРОЧНАЯ СОВОКУПНОСТЬ ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ x 1, x 2, … и xk – ВАРИАНТЫ; n 1, n 2, … и nk – ЧАСТОТЫ. Сумма всех частот равна объему выборки: ОТНОСИТЕЛЬНАЯ ЧАСТОТА – отношение частоты к объему выборки. РАНЖИРОВАННЫЙ СТАТИСТИЧЕСКИЙ РЯД – совокупность всех значений в выборке, расположенных в определенном порядке. ДИСКРЕТНОЕ СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ или ВАРИАЦИОННЫЙ РЯД – совокупность всех вариант и соответствующих им частот или относительных частот. x 1 x 2 ··· xk n 1 n 2 ··· n p* nk p*1 p*2 ПОЛИГОН ЧАСТОТ p*k x

ХАРАКТЕРИСТИКИ СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ МОДА (Мо) – варианта, которой соответствует набольшая частота. МЕДИАНА (Ме) – варианта, которая расположена в середине статистического распределения. , если n – нечетное число; , если n – четное число. ВЫБОРОЧНАЯ СРЕДНЯЯ ( ) – среднее арифметическое значение вариант статистического распределения.

ХАРАКТЕРИСТИКИ СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ ВЫБОРОЧНАЯ ДИСПЕРСИЯ ( ) – среднее арифметическое квадратов отклонения вариант от их среднего значения. ВЫБОРОЧНОЕ СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ ( ) – корень квадратный из выборочной дисперсии.

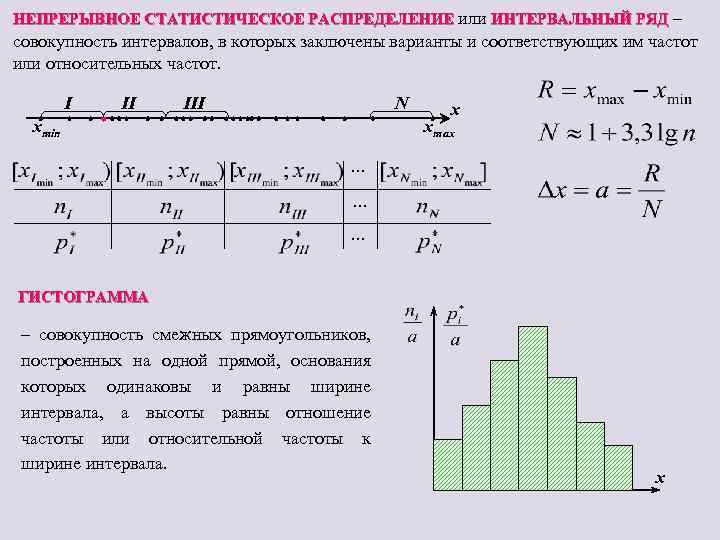НЕПРЕРЫВНОЕ СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ или ИНТЕРВАЛЬНЫЙ РЯД – совокупность интервалов, в которых заключены варианты и соответствующих им частот или относительных частот. I II III N xmin x xmax ··· ··· ГИСТОГРАММА – совокупность смежных прямоугольников, построенных на одной прямой, основания которых одинаковы и равны ширине интервала, а высоты равны отношение частоты или относительной частоты к ширине интервала. x

ОЦЕНКА ПАРАМЕТРОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ПО ЕЕ ВЫБОРКЕ ГЕНЕРАЛЬНАЯ СРЕДНЯЯ – среднее арифметическое всех значений, составляющих генеральную совокупность. ГЕНЕРАЛЬНОЕ СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ – среднее арифметическое квадратов отклонения вариант от генеральной средней. Точечная оценка

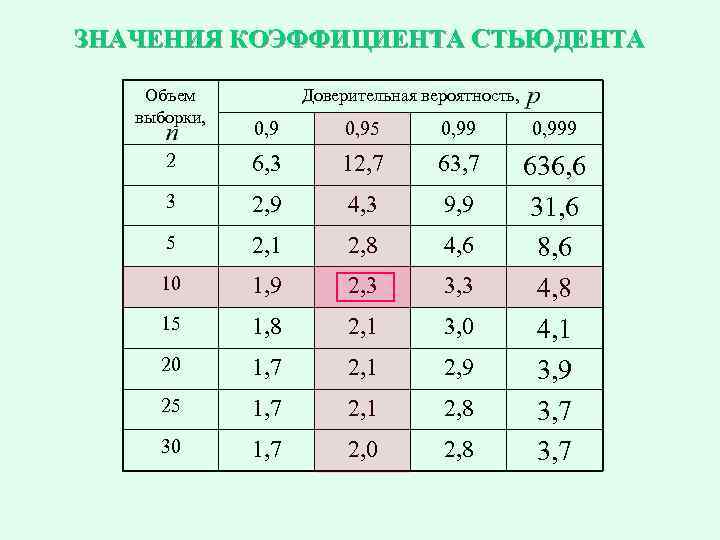ЗНАЧЕНИЯ КОЭФФИЦИЕНТА СТЬЮДЕНТА Объем выборки, Доверительная вероятность, 0, 95 0, 999 2 6, 3 12, 7 63, 7 3 2, 9 4, 3 9, 9 5 2, 1 2, 8 4, 6 10 1, 9 2, 3 3, 3 15 1, 8 2, 1 3, 0 20 1, 7 2, 1 2, 9 25 1, 7 2, 1 2, 8 30 1, 7 2, 0 2, 8 636, 6 31, 6 8, 6 4, 8 4, 1 3, 9 3, 7