Лектор к т н доцент кафедры ОПД

Лектор к. т. н. , доцент кафедры ОПД ТС Будылдина Н. В.

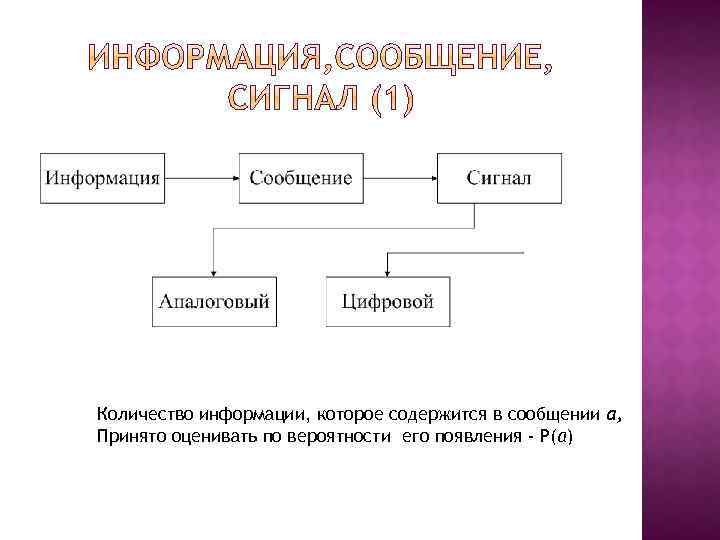Количество информации, которое содержится в сообщении а, Принято оценивать по вероятности его появления - Р(а)

ИНФОРМАЦИЯ Совокупность сведений о каком – нибудь явлении или объекте , которые увеличивают наши знания об этом явлении или объекте

Единица информации – количество информации, заключенное в выборе одного из двух равновероятностных событий. Bit - binary digit Ii=log 2(1/pi)=-log 2 pi при pi=0, 5, I=1

Ценность информации = log 2 (Pi/P 0)>0 P 0 – вероятность достижения цели до получения информации; Pi - вероятность достижения цели после получения информации.

СООБЩЕНИЕ Сообщение представления удобная для расстояние. – форма информации, передачи на

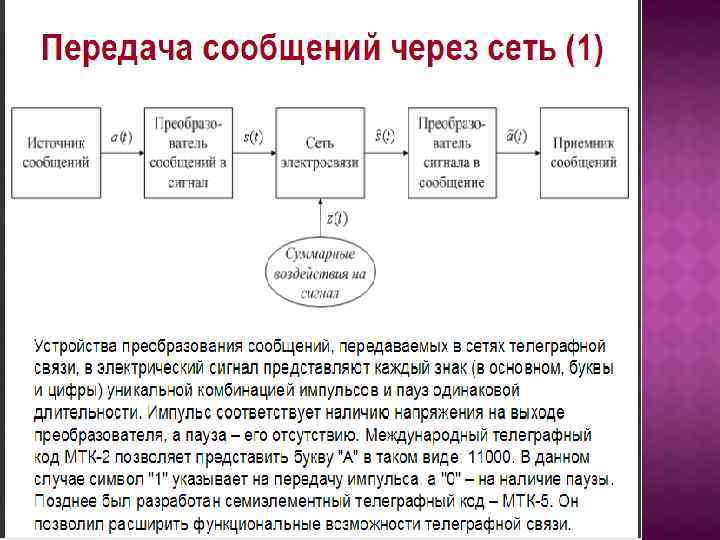
СИГНАЛ Сигнал – физический процесс, отображающий передаваемое сообщение. Отображение сообщения обеспечивается изменением какой-либо физической величины, характеризующей процесс. (Эта величина является информационным параметром сигнала).

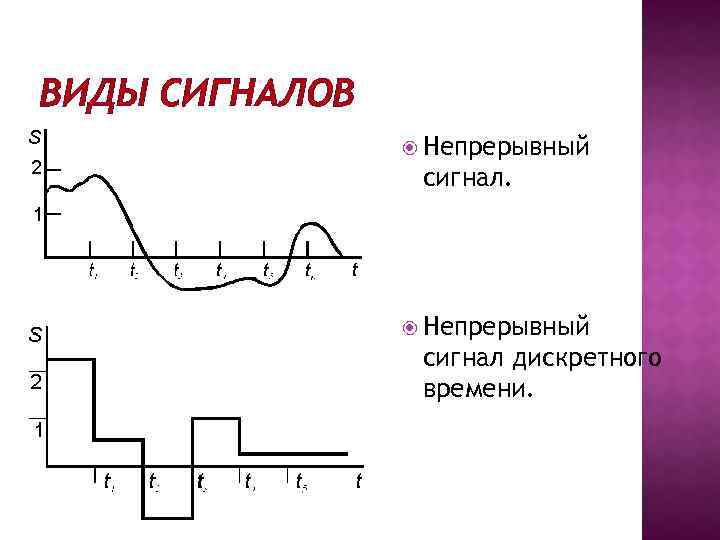ВИДЫ СИГНАЛОВ Непрерывный сигнал дискретного времени.

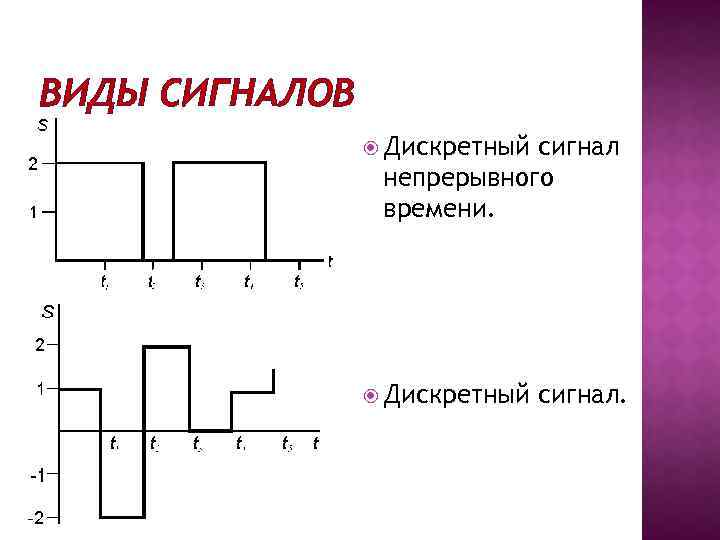ВИДЫ СИГНАЛОВ Дискретный сигнал непрерывного времени. Дискретный сигнал.

Непрерывные сигналы непрерывного времени называют сокращенно непрерывными (аналоговыми) сигналами. Они могут изменяться в произвольные моменты, принимая любые значения из непрерывного множества возможных значений. К таким сигналам относится и известная всем синусоида. Непрерывные сигналы дискретного времени могут принимать произвольные значения, но изменяться только в определенные, наперед заданные (дискретные) моменты t 1, t 2, t 3, . . Дискретные сигналы непрерывного времени отличаются тем, что они могут изменяться в произвольные моменты, но их величины принимают только разрешенные (дискретные) значения. Дискретные сигналы дискретного времени (сокращенно дискретные) в дискретные моменты времени могут принимать только разрешенные (дискретные) значения.

СПЕКТРЫ Все сигналы могут быть подразделены на периодические и непериодические. Периодическим называется сигнал, значения которого повторяются через определенные равные промежутки времени, называемые периодом повторения сигнала, или просто периодом. Для непериодического сигнала это условие не выполняется.

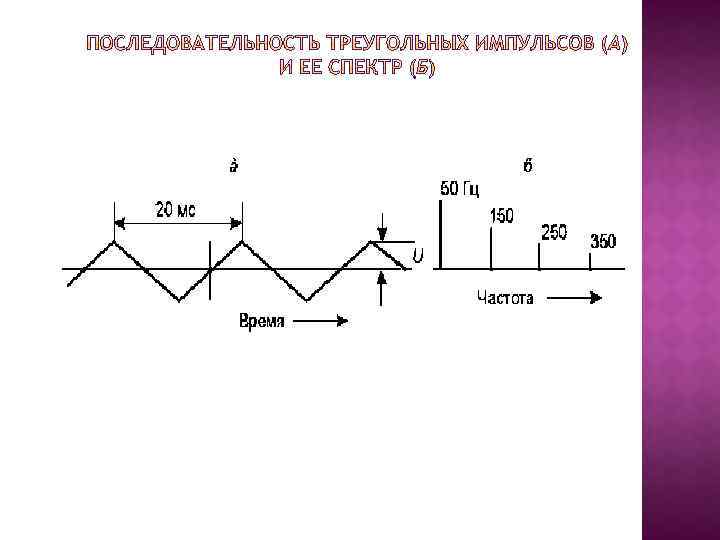
СПЕКТРЫ ПЕРИОДИЧЕСКИХ СИГНАЛОВ Простейшим периодическим сигналом является гармоническое колебание. s(t)=S sin t, где S, – амплитуда и угловая частота колебания. Другим примером периодического сигнала является последовательность прямоугольных импульсов:

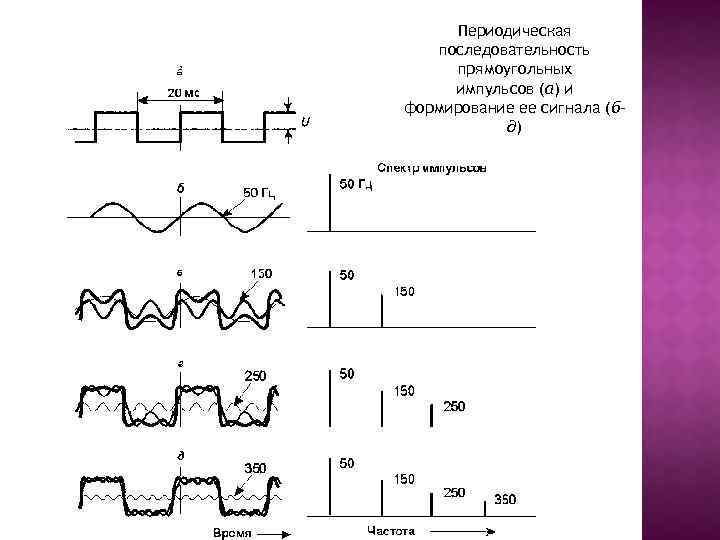Периодическая последовательность прямоугольных импульсов (а) и формирование ее сигнала (б– д)

Тот факт, что сигнал произвольной формы (а не только прямоугольные импульсы) можно «разложить» на сумму обыкновенных синусоид, впервые доказал в 20 -х годах прошлого века французский математик Ж. Фурье. Такой набор синусоид получил название спектра сигнала. Каждый сигнал (отличающийся от других по форме) имеет свой сугубо индивидуальный спектр, т. е. может быть получен только из синусоид со строго определенными частотами и амплитудами.

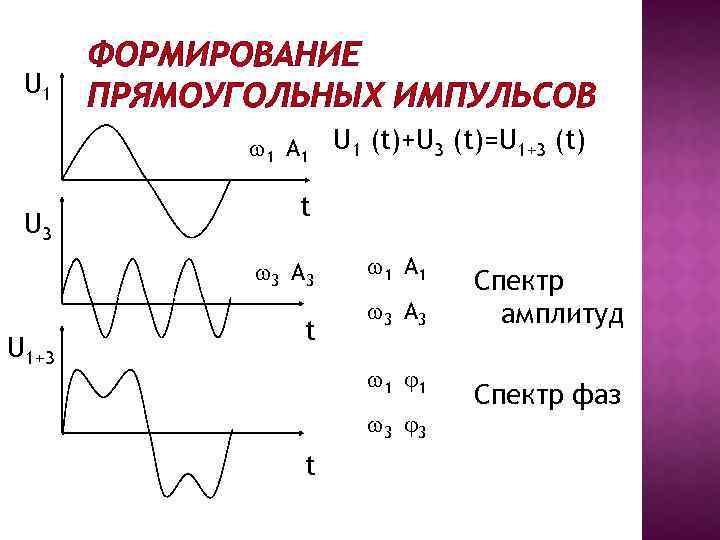U 1 ФОРМИРОВАНИЕ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ 1 A 1 U 3 t 3 A 3 U 1+3 U 1 (t)+U 3 (t)=U 1+3 (t) t 1 A 1 3 A 3 1 1 3 3 t Спектр амплитуд Спектр фаз

Это выражение показывает, что любой периодический сигнал состоит из гармоник. В математике эту формулу называют рядом Фурье. Если изобразить амплитуду и фазу каждой гармоники на рисунке, то получим так называемые спектральные диаграммы сигнала, где линии, соответствующие амплитудам и фазам гармоник, называются спектральными линиями. Распределение амплитуд гармоник по частоте называется спектром амплитуд этого сигнала, а распределение фаз – спектром фаз. Когда интересуют не значения амплитуд и начальных фаз гармоник сложного колебания, а только их частоты, то следует говорить о спектре частот сигнала.

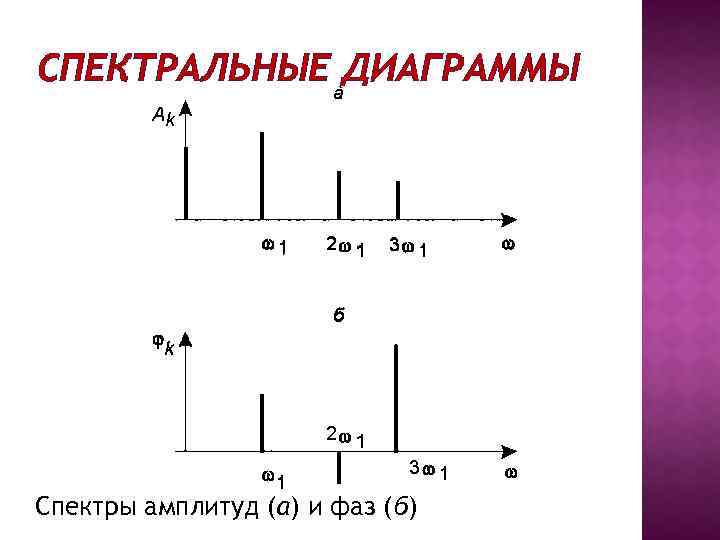СПЕКТРАЛЬНЫЕ ДИАГРАММЫ Спектры амплитуд (а) и фаз (б)

Так как спектр периодического сигнала состоит из отдельных спектральных линий, его называют дискретным.

СПЕКТРЫ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ Непериодический сигнал легко получить из периодического, увеличивая период вплоть до

При переходе к непериодическому сигналу (например, к одиночному импульсу) мы получаем в спектре такого сигнала вместо отдельных гармоник бесконечно большое число синусоидальных колебаний с бесконечно близкими частотами, заполняющими всю шкалу частот. Причем амплитуда каждого такого колебания становится исчезающе малой, потому что на его долю приходится бесконечно малая часть энергии сигнала. Другими словами, в любой бесконечно узкой полосе частот мы всегда обнаружим синусоидальное колебание, правда, бесконечно малой амплитуды.

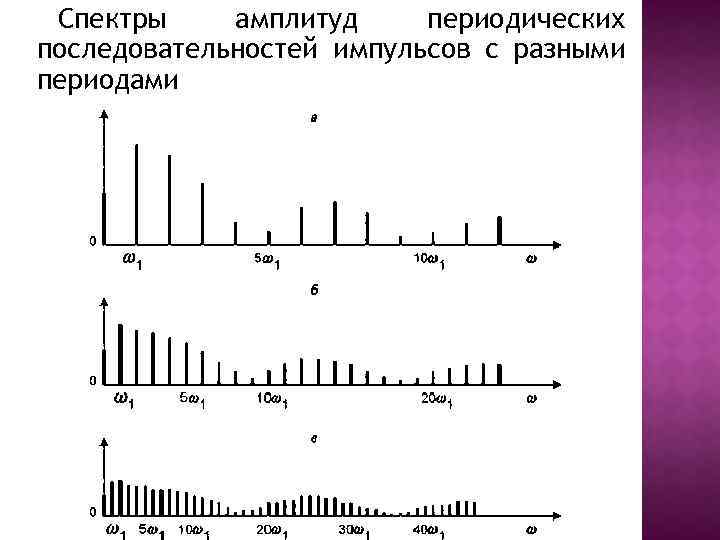Спектры амплитуд периодических последовательностей импульсов с разными периодами

Спектр непериодического сигнала является в общем случае не дискретным, а непрерывным.