Лек.11 Исследования с помощью производной.ppt
- Количество слайдов: 19

Лектор Буганова С. Н. Исследование функций и построение их графиков Дисциплина Математика 1 Лекция 11 2015 -16 учебный год

План Исследование функции на монотонность: 1. Определение монотонности 2. Необходимый и достаточный признаки возрастания, убывания функции 3. Экстремумы функции 4. Алгоритм исследования функции на экстремумы и промежутки монотонности Исследования функции на выпуклость, вогнутость: 1. Определение выпуклости функции вверх и вниз 2. Достаточное условие выпуклости функции на интервале 3. Точка перегиба 4. Достаточный признак существования точки перегиба Асимптоты

Схема исследования функции. 1. Область определения D(y), область значения E(y) функции. 2. Четность, нечетность функции. 3. Периодичность. 4. Точки пересечения с осями координат. 5. Монотонность. Экстремумы функции. 6. Точки перегиба. Выпуклость функции. 7. Асимптоты. 8. График.

Функция y = f(x) называется монотонно возрастающей на интервале (a, b), если для любых х1 и x 2, принадлежащих этому интервалу, из неравенства x 2 > х1 сле дует неравенствоf(x 2) > f(x 1). ∀x 1, x 2∈(a, b) при x 1< x 2 f(x 1)<f(x 2); Функция y = f(x) называется монотонно убывающей на интервале (а, b), если для любых х1 и x 2, принадлежащих этому интервалу, из неравенства x 2 > x 1 следует неравенство f(x 2)< f(x 1). Естественно, что интервал (a, b) предполагается взятым из области определения функции. ∀x 1, x 2∈(a, b) при x 1< x 2 f(x 1)>f(x 2).
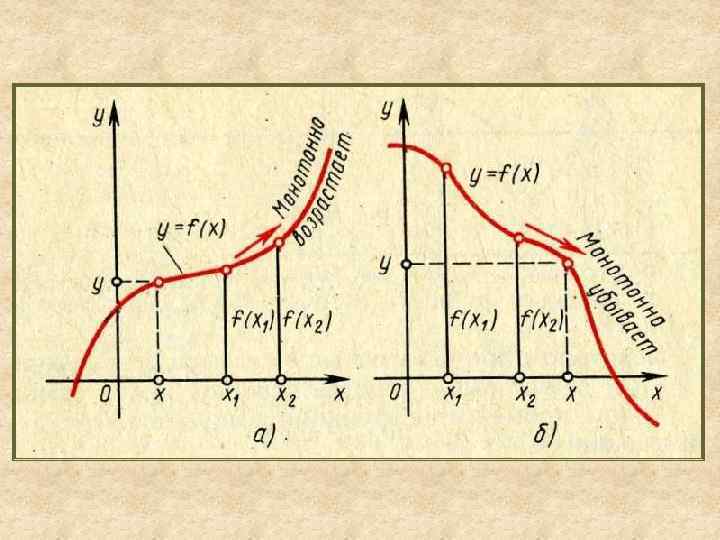

Необходимый и достаточный признаки возрастания (убывания) функции Теорема: Если дифференцируемая функция возрастает (убывает) на некотором интервале, то ее производная неотрицательная (неположительная) на этом интервале. Теорема : Если производная функции на некотором интервале положительна (отрицательна), то функция возрастает (убывает) на этом интервале.

Определение. Точки, в которых f '(x) =0 или не существует, называются критическими точками I рода. Теорема. (1 -ый достаточный признак существования экстремума) Пусть y=f(x) непрерывна в интервале, содержащем критическую точку x 0, дифференцируема во всех точках этого интервала, кроме может быть самой x 0, тогда: а) если при переходе слева направо через x 0 производная f'(x) меняет знак с «+» на «-» , то в точке x 0 функция f(x) имеет максимум; b) если знак производной меняется с «-» на «+» , то в точке x 0 функция f(x) имеет минимум.

Алгоритм исследования функции на экстремумы и промежутки монотонности 1. Находим производную f ’(x) 2. Находим точки, в которых f ’(x)=0 или f’(x) не существует 3. Разбиваем этими точками область определения f(x) на промежутки 4. Методом проб определяем знак f ’(x) в этих промежутках и находим интервалы монотонности 5. Применяем достаточное условие экстремума.

Исследование функции на выпуклость, вогнутость 1. Выпуклость вверх и вниз Говорят, что функция y = f(x) выпукла вверх (выпуклая) в точке x 0, если существует окрестность точки x 0 такая, что для всех ее точек х касательная к графику функции в точке M 0(x 0; y 0) лежит выше графика. Говорят, что функция y = f(x) выпукла вниз (вогнутая) в точке x 0, если существует окрестность точки х0 такая, что для всех ее точек х касательная к графику функции в точке M 0(x 0; y 0) лежит ниже графика.
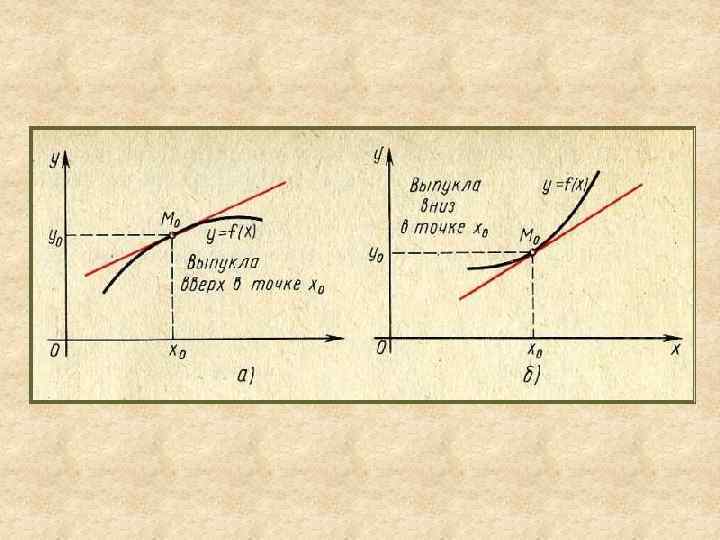

2. Достаточное условие выпуклости функции на интервале. Если вторая производная f (x) существуют на интервале (а, b) и не меняет знак на этом интервале, то: 1) при f (x) > 0 (знак +) функция f(x) выпукла вниз на интервале (a, b); 2) при f (x) < 0 (знак ) функция f(x) выпукла вверх на интервале (a, b).
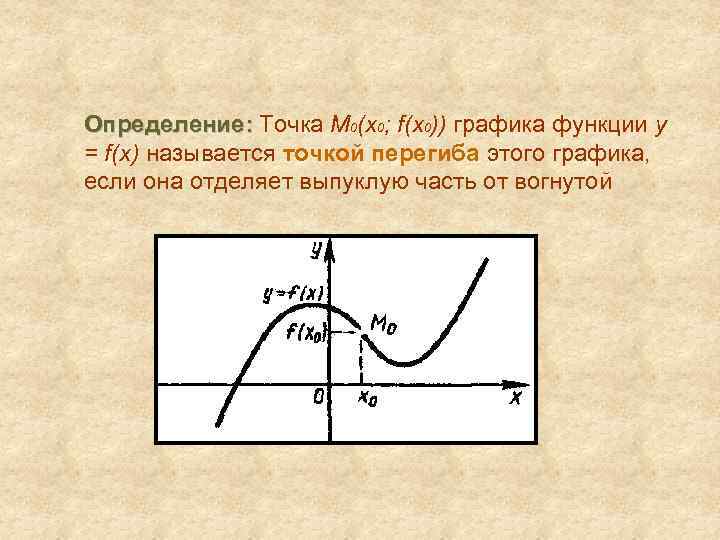
Определение: Точка М 0(х0; f(x 0)) графика функции y = f(x) называется точкой перегиба этого графика, если она отделяет выпуклую часть от вогнутой

Достаточный признак существования точки перегиба Определение: Точки, в которых вторая производная обращается в нуль или не существует, называются критическими точками 2 -го рода. В этих точках перегиб может быть, а может и не быть. Если для функции y=f(x) вторая производная ее f”(x) в некоторой точке x 0 обращается в нуль и при переходе через точку меняет свой знак на обратный, то точка М(х0; f(x 0)) является точкой перегиба функции.

Асимптоты Определение 1: Если расстояние от точки М кривой y = f(x) до некоторой определенной прямой при x x 0 и неограниченном удалении точки М от начала координат стремится к нулю, то эта прямая называется асимптотой кривой.
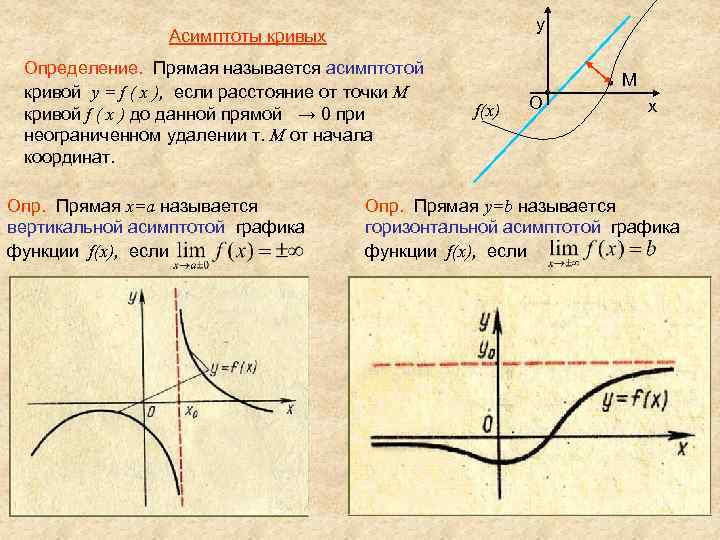
y Асимптоты кривых Определение. Прямая называется асимптотой кривой y = f ( x ), если расстояние от точки M кривой f ( x ) до данной прямой → 0 при неограниченном удалении т. М от начала координат. Опр. Прямая x=a называется вертикальной асимптотой графика функции f(x), если M f(x) O x Опр. Прямая y=b называется горизонтальной асимптотой графика функции f(x), если
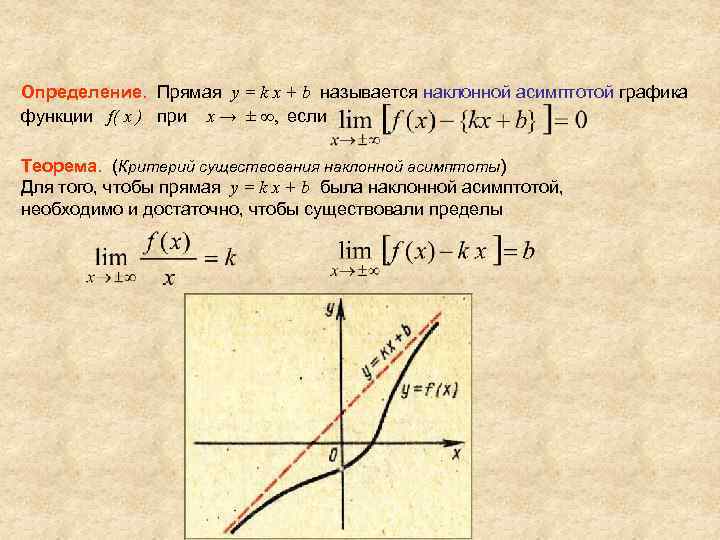
Определение. Прямая y = k x + b называется наклонной асимптотой графика функции f( x ) при x → ± ∞, если Теорема. (Критерий существования наклонной асимптоты) Для того, чтобы прямая y = k x + b была наклонной асимптотой, необходимо и достаточно, чтобы существовали пределы

Задание на СРС 1. . Наибольшее и наименьшее значения функции на отрезке. [1 с. 200]. Задание на СРСП 1. ИДЗ 6. 4. [1, с. 240].
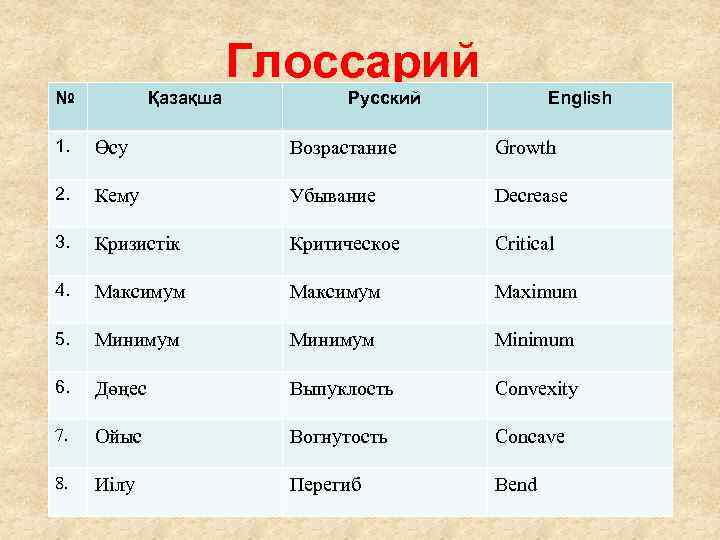
Глоссарий № Қазақша Русский English 1. Өсу Возрастание Growth 2. Кему Убывание Decrease 3. Кризистік Критическое Critical 4. Максимум Maximum 5. Минимум Minimum 6. Дөңес Выпуклость Convexity 7. Ойыс Вогнутость Concave 8. Иілу Перегиб Bend

Основная 1. А. П. Рябушко. Индивидуальные задания по высшей математике, т. 1. - Мн. : Выш. Школа, 2011. 2. Данко П. Е. , Попов А. Г. Высшая математика в упражнениях и задачах: Учебное пособие для втузов. - М. : Оникс, 2007. Дополнительная 3. Сыдыкова Д. К. Математика I. Методическое руководство к выполнению заданий для СРС. -Алматы: Каз. ГАСА, 2008. 4. Сыдыкова Д. К. «Курс Математики- I» , Модуль I, II для дистанционного обучения. Электронный учебник. -Алматы: Каз. ГАСА, 2012. 5. www. studentlibrary. ru 6. http: //sferaznaniy. ru/vysshaya-matematika.
Лек.11 Исследования с помощью производной.ppt