Лекция заключительная обзорная 1 Тепловое излучение Испускание

Лекция заключительная, обзорная. 1

Тепловое излучение Испускание электромагнитных волн за счет внутренней энергии тела Тепловое излучение – наиболее распространенный вид излучения, который имеет место при любой температуре Тепловое излучение – равновесный процесс

Тепловое излучение Количество энергии, испущенное единицей поверхности за единицу времени (поток энергии) в пределах полусферы называют энергетической светимостью и обозначают R.

Тепловое излучение Закон Стефана - Больцмана Энергетическая светимость пропорциональна четвёртоё степени температуры Постоянная Стефана – Больцмана равна

Тепловое излучение Закон смещения Вина В 1893 году Вин установил, что длина волны, соответствующая максимуму функции спектрального распределения связанна с температурой соотношением – постоянная в законе смещения Вина.

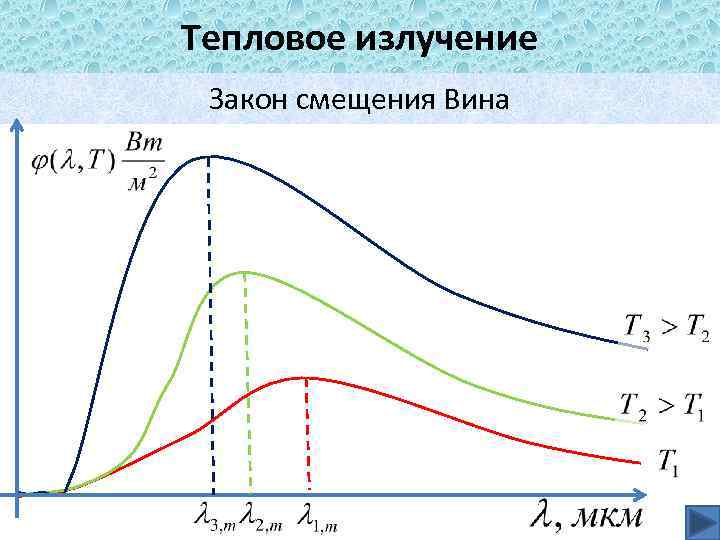
Тепловое излучение Закон смещения Вина

Тепловое излучение Формула Планка

Уравнение Эйнштейна для фотоэффекта

Тормозное рентгеновское излучение

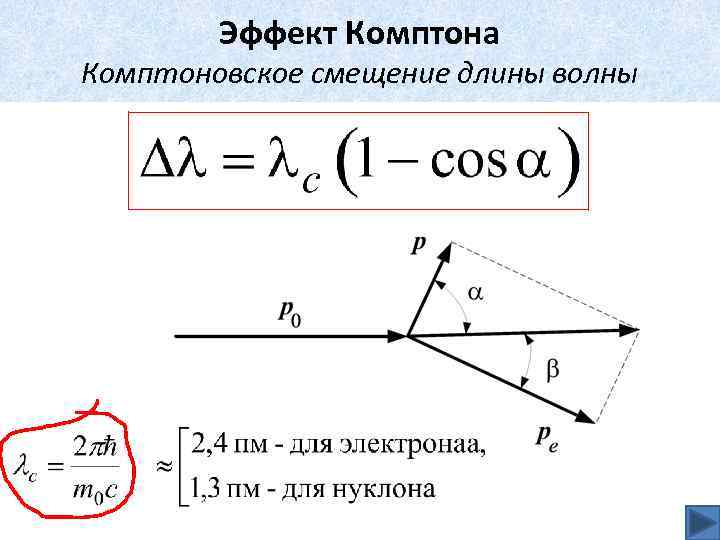
Эффект Комптона Комптоновское смещение длины волны

Принцип неопределенности Соотношение неопределённостей Гейзенберга

Волновые свойства частиц Луи Де Бройль (1892 -1987) 1924 г. § Выдвинул гипотезу о корпускулярно-волновом дуализме электронов, атомов и других микрочастиц § Нобелевская премия 1929 г.

Волновые свойства частиц , Дебройлевская длина волны У каждой частицы длина и частота волны связанны такими же соотношениями, как и у фотона Длина волны де Бройля

Гипотеза де Бройля Каждой частице можно поставить в соответствие волну вероятности Длина этой волны определяется соотношением

Смысл пси-функции Интенсивность волны пропорциональна квадрату амплитуды. Поэтому мы говорим только о квадрате модуля амплитуды волновой функции который имеет смысл плотности вероятности.

Смысл пси-функции ИТАК: Величина есть плотность вероятности, а величина - вероятность обнаружить частицу в объеме

Волновое уравнение – уравнение Шрёдингера Поскольку пси-функция является волной, то она должна удовлетворять волновому уравнению:

Волновое уравнение – уравнение Шрёдингера Стационарное, то есть независящее от времени, решение – стационарное уравнение Шрёдингера. Его надо выучить.

Волновое уравнение – уравнение Шрёдингера Используя оператор Лапласа, уравнение можно переписать в виде или Эти уравнения тоже лучше выучить.

Решение уравнения Шрёдингера Рассмотрим одномерный случай для частицы, находящейся в потенциальной яме шириной l с бесконечно высокими стенками. За пределы ямы частица попасть не может, поэтому вероятность обнаружения частицы вне ямы равна нулю.

Уравнение Шрёдингера для линейного гармонического осцилятора Если колебания осциллятора происходят под действием некоторой квазиупругой силы то его потенциальная энергия может быть записана в виде 21

Уравнение Шрёдингера для линейного гармонического осцилятора Частота колебаний такого осциллятора аналогична частоте колебаний груза напружине: откуда и, следовательно, 22

Уравнение Шрёдингера для линейного гармонического осциллятора Из стационарного уравнения Шрёдингера и выражения для потенциальной энергии Получаем уравнение Шрёдингера для гармонического осциллятора: 23

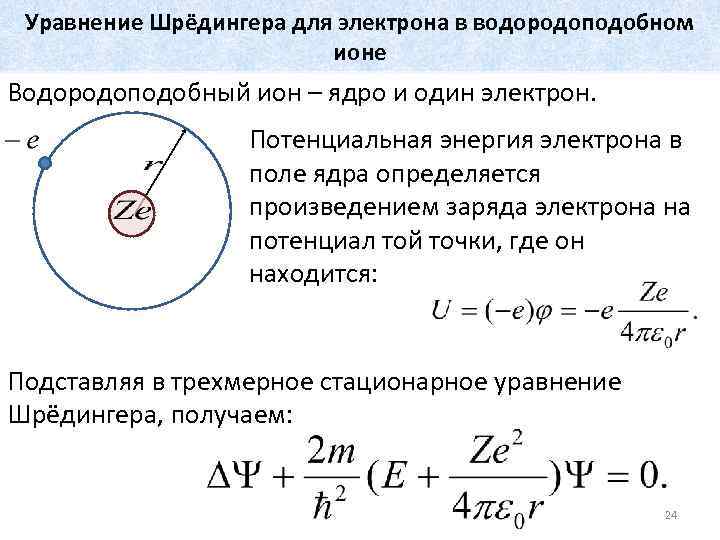
Уравнение Шрёдингера для электрона в водородоподобном ионе Водородоподобный ион – ядро и один электрон. Потенциальная энергия электрона в поле ядра определяется произведением заряда электрона на потенциал той точки, где он находится: Подставляя в трехмерное стационарное уравнение Шрёдингера, получаем: 24

Характерные признаки разных уравнений Трёхмерный случай. Стационарное уравнение. Одномерный случай. Стационарное уравнение. Трёхмерный случай. нестационарное уравнение. 25

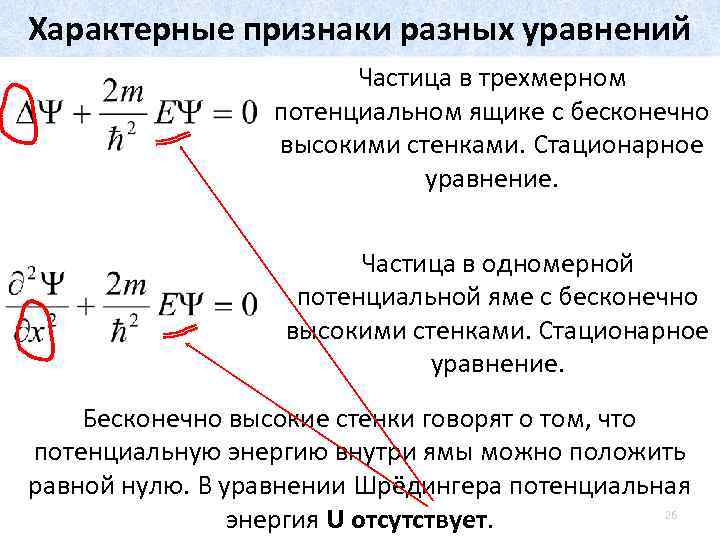
Характерные признаки разных уравнений Частица в трехмерном потенциальном ящике с бесконечно высокими стенками. Стационарное уравнение. Частица в одномерной потенциальной яме с бесконечно высокими стенками. Стационарное уравнение. Бесконечно высокие стенки говорят о том, что потенциальную энергию внутри ямы можно положить равной нулю. В уравнении Шрёдингера потенциальная 26 энергия U отсутствует.

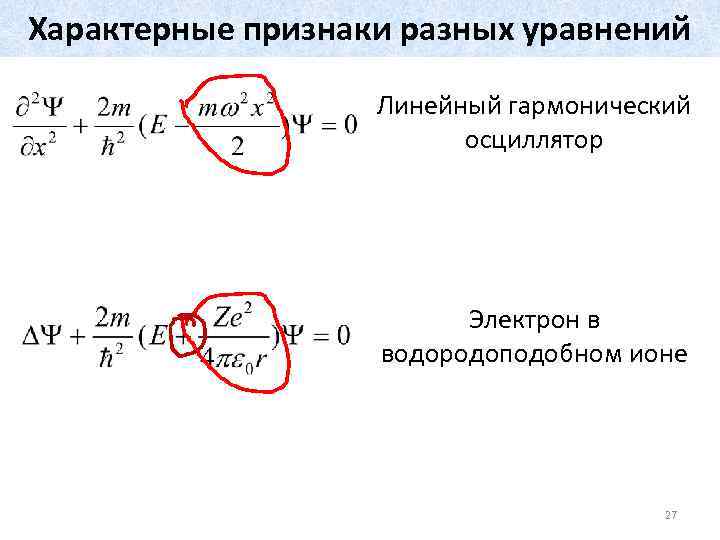
Характерные признаки разных уравнений Линейный гармонический осциллятор Электрон в водородоподобном ионе 27

Постулаты Бора • Из бесконечного множества электронных орбит осуществляются только некоторые, находясь на которых электрон, несмотря на то, что движется с ускорением, не излучает энергии • Излучение испускается и поглощается в виде светового кванта только при переходе электрона из одного стационарного состояния в другое: • Момент импульса электрона на стационарных орбитах может приобретать только значения, кратные постоянной Планка:

Нильс Бор (1885 -1962) 1913 Усовершенствована планетарная модель атома водорода на основании постулатов Бора: • Электрон в атоме может двигаться по некоторым устойчивым орбитам без излучения. • Излучение (поглощение) энергии происходит при переходе электрона с одной стационарной орбиты на другую • Нобелевская премия 1922 г. hν e

ВАЖНО Радиус орбиты пропорционален квадрату её номера (главного квантового числа) Энергия электрона на орбите обратно пропорциональна квадрату её номера (главного квантового числа)

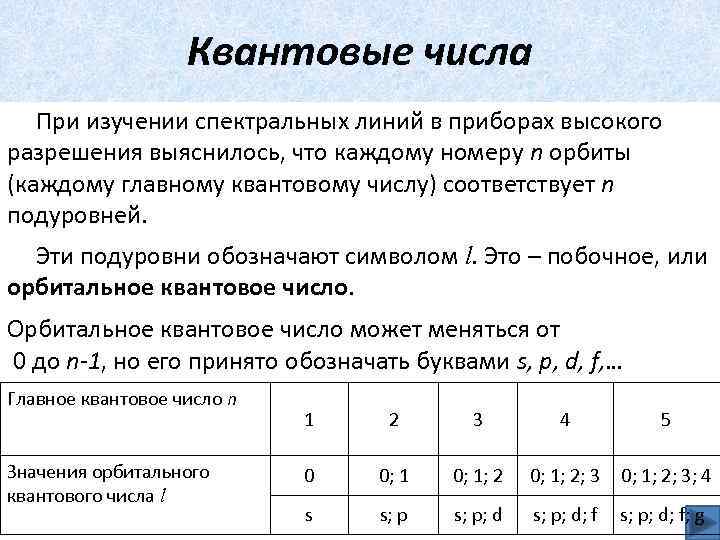
Квантовые числа При изучении спектральных линий в приборах высокого разрешения выяснилось, что каждому номеру n орбиты (каждому главному квантовому числу) соответствует n подуровней. Эти подуровни обозначают символом l. Это – побочное, или орбитальное квантовое число. Орбитальное квантовое число может меняться от 0 до n-1, но его принято обозначать буквами s, p, d, f, … Главное квантовое число n Значения орбитального квантового числа l 1 2 3 4 5 0 0; 1; 2; 3; 4 s s; p; d; f; g

Квантовые числа Орбитальное квантовое число отвечает за форму орбиты и, соответственно, за орбитальный момент импульса электрона

Квантовые числа Орбитальное квантовое число отвечает за форму орбиты и, соответственно, за орбитальный момент импульса электрона Орбитальный момент импульса определяется формулой и минимален в s состоянии

Квантовые числа Движение электрона по орбите представляет собой ток, а значит существует орбитальный магнитный момент. Этот магнитный момент может быть по разному ориентирован в пространстве. Каждой ориентации орбитального магнитного момента отвечает своё магнитное квантовое число m. Каждому значению орбитального квантового числа l соответствует свой набор значений магнитного квантового числа m в интервале (-l… 0…l)

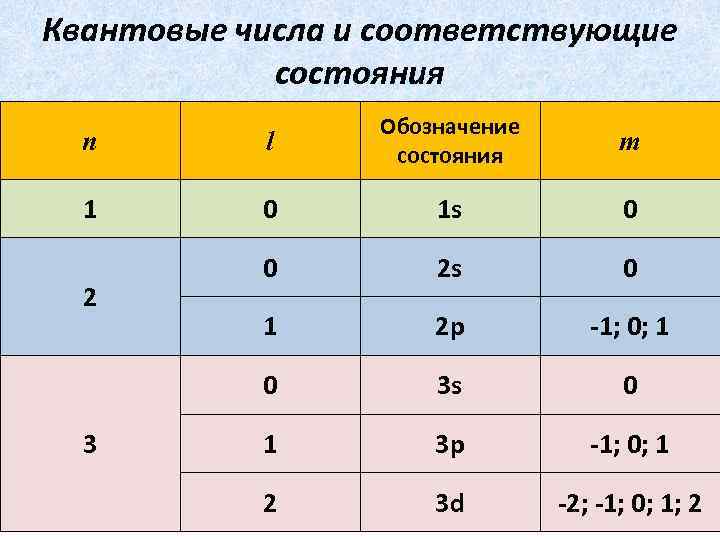
Квантовые числа и соответствующие состояния n l Обозначение состояния 1 0 1 s 0 0 2 s 0 1 2 p -1; 0; 1 0 3 s 0 1 3 p -1; 0; 1 2 3 d -2; -1; 0; 1; 2 2 3 m

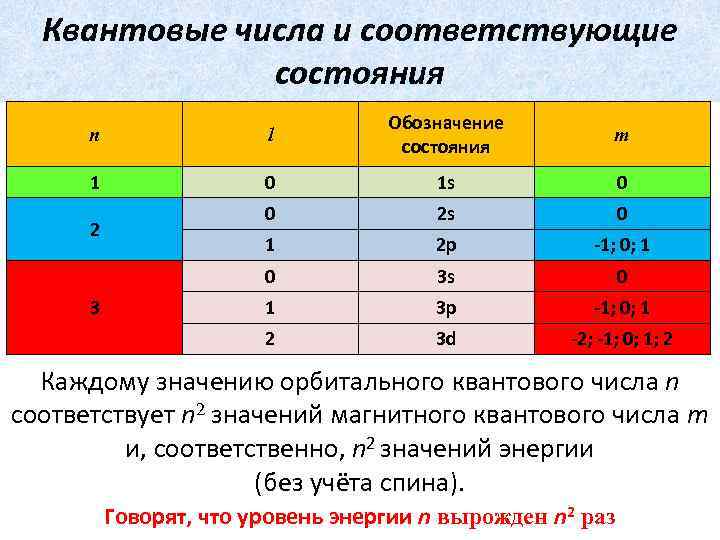
Квантовые числа и соответствующие состояния n l Обозначение состояния m 1 0 1 s 0 0 2 s 0 1 2 p -1; 0; 1 0 3 s 0 1 3 p -1; 0; 1 2 3 d -2; -1; 0; 1; 2 2 3 Каждому значению орбитального квантового числа n соответствует n 2 значений магнитного квантового числа m и, соответственно, n 2 значений энергии (без учёта спина). Говорят, что уровень энергии n вырожден n 2 раз

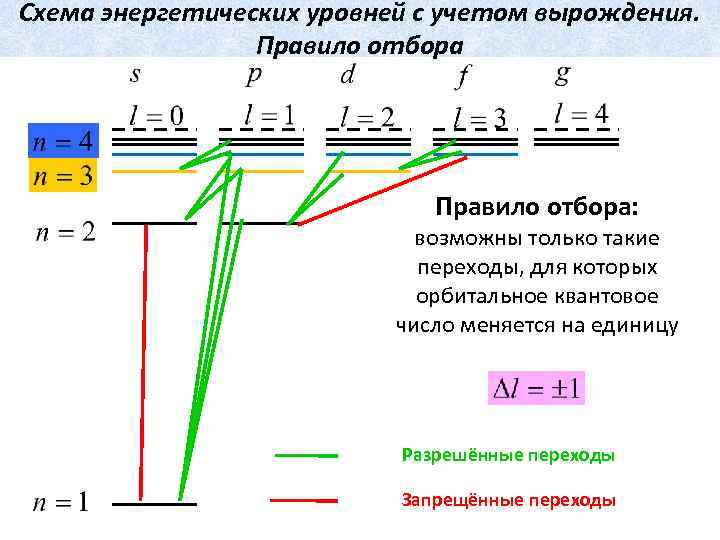
Схема энергетических уровней с учетом вырождения. Правило отбора: возможны только такие переходы, для которых орбитальное квантовое число меняется на единицу Разрешённые переходы Запрещённые переходы

38