Лекция Прогнозирование с помощью тренд-сезонных моделей Выделение сезонной

Лекция. Прогнозирование с помощью тренд-сезонных моделей Выделение сезонной составляющей временного ряда. Мультипликативные модели. Аддитивные модели

Выделение сезонной составляющей временного ряда В настоящее время при описании и прогнозировании тренд-сезонных процессов используются подходы, связанные с применением индексов сезонности в сочетании с кривыми роста; процедуры, опирающиеся на широкий спектр адаптивных моделей; сезонный вариант модели ARIMA и др. , а также разрабатываются специализированные подходы, учитывающие специфику конкретных временных рядов.

Выделение сезонной составляющей временного ряда Процедура расчета зависит от принятой модели временного ряда, содержащей сезонность в аддитивной или мультипликативной форме. При этом для аддитивной модели характеристики сезонности будут измеряться в абсолютных величинах, а для мультипликативной — в относительных.

Алгоритм оценивания сезонной компоненты Элиминирование (ла т. eliminare — изгонять) — исключение из рассмотрения в процессе расчета факторов, заведомо не связанных с изучаемым явлением.

Алгоритм расчета. Мультипликативная сезонность

Алгоритм расчета. Мультипликативная сезонность

Алгоритм расчета. Аддитивная сезонность

Прогнозирование с помощью тренд-сезонных моделей Часто используемый на практике подход к прогнозированию с помощью тренд-сезонных моделей может быть описан в виде следующей последовательности шагов: 1 • Оценивание сезонной составляющей с учетом характера сезонности (аддитивной или мультипликативной). 2 • Десезонализация (сезонная корректировка) исходных данных. 3 • Расчет параметров тренда на основе временного ряда, полученного на втором шаге. 4 • Моделирование динамики исходного ряда с учетом трендовой и сезонной составляющих.

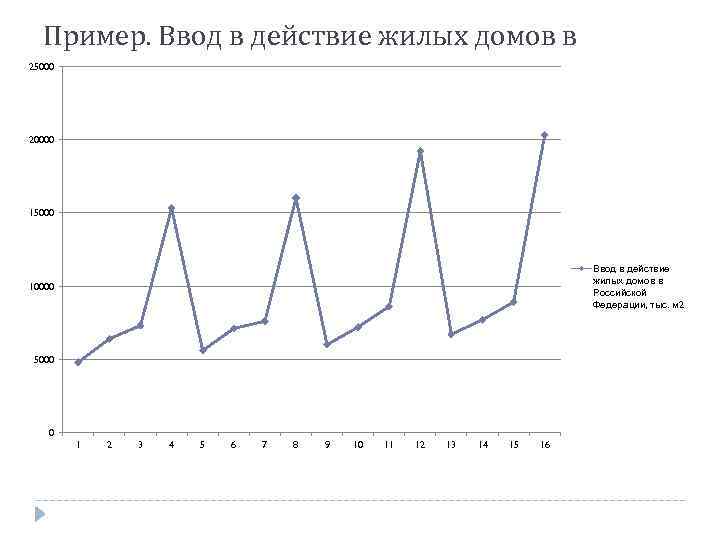Пример. Ввод в действие жилых домов в Российской Федерации 25000 Год Кварта л 20000 Год I 2 6400 III 3 7300 IV 15000 4800 II 2002 1 4 15 300 I 7100 7 7600 IV 5000 6 8 I 10 7200 11 8600 IV 12 19 200 I 13 II 14 Ввод в действие жилых домов в Российской Федерации, тыс. м 2 III 15 8900 IV 16 000 6000 III 2005 9 II 2004 5600 III 2003 5 II 10000 Кварта л 16 20 300 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 6700 7700

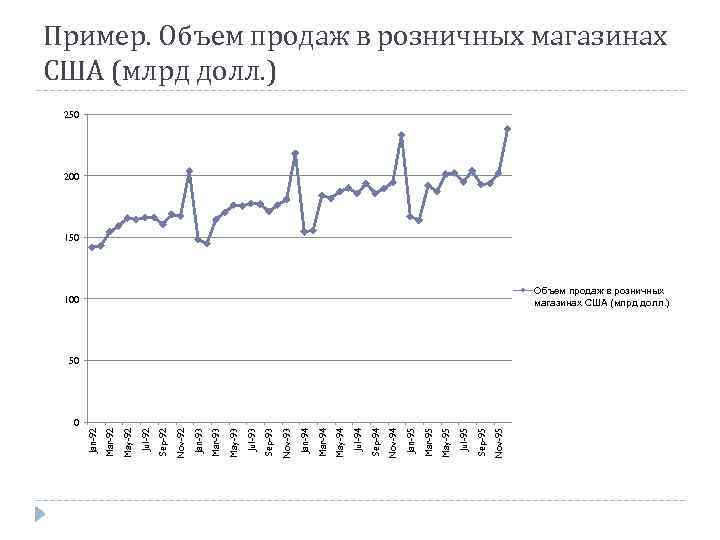Пример. Объем продаж в розничных магазинах США (млрд долл. ) 164, 6 184, 2 192, 1 Апрель 159, 1 170, 3 181, 8 187, 5 Май 165, 8 176, 1 187, 2 201, 4 Июнь 164, 6 175, 7 190, 1 Июль 166 177, 7 185, 8 Август 166, 3 177, 1 193, 8 204, 2 Сентябрь 160, 6 171, 1 185, 9 192, 8 Октябрь 168, 7 176, 4 189, 7 194 Ноябрь 167, 2 180, 9 194, 7 202, 4 233, 3 238 150 100 50 Jan-93 Nov-92 Sep-92 Декабрь Jul-92 May-92 Mar-92 Jan-92 0 204, 1 218, 3 Nov-95 154, 7 Sep-95 Март Jul-95 164 May-95 155, 8 Mar-95 145 Jan-95 143, 1 Nov-94 Февраль 200 Sep-94 167 Jul-94 154, 6 May-94 148, 4 Mar-94 142, 1 Jan-94 Январь Nov-93 1995 г. Sep-93 1994 г. Jul-93 1993 г. May-93 1992 г. Mar-93 Месяц 250 202, 6 Объем продаж в розничных магазинах США (млрд долл. ) 194, 9

Оценка точности выбранных моделей прогнозирования Важнейшими характеристиками качества модели, выбранной для прогнозирования, являются показатели ее точности. Они описывают величины ошибок, полученных при использовании модели. Таким образом, чтобы судить о качестве выбранной модели, необходимо проанализировать систему показателей, характеризующих как адекватность модели, так и ее точность.

Абсолютная ошибка прогноза

Mean Absolute Derivation, MAD

Относительная ошибка прогноза

Mean Absolute Percentage Error (МАРЕ)

Средняя квадратическая ошибка

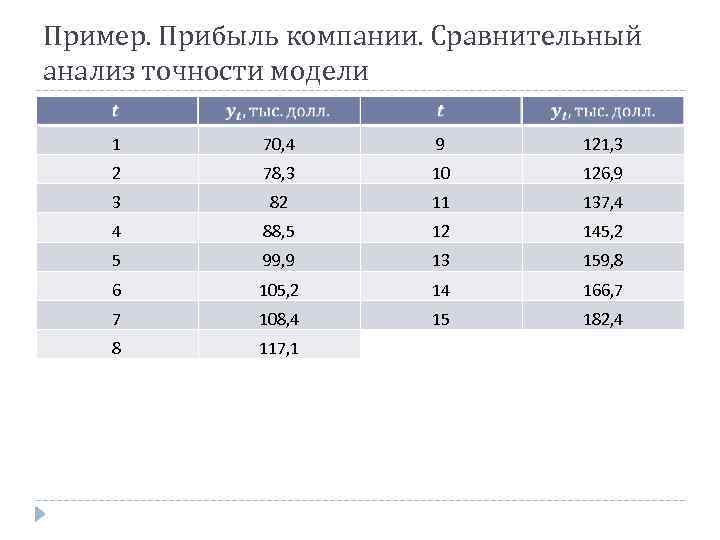Пример. Прибыль компании. Сравнительный анализ точности модели 1 70, 4 9 121, 3 2 78, 3 10 126, 9 3 82 11 137, 4 4 88, 5 12 145, 2 5 99, 9 13 159, 8 6 105, 2 14 166, 7 7 108, 4 15 182, 4 8 117, 1

Оценка точности выбранных моделей прогнозирования Чем меньше значения всех рассмотренных характеристик, тем выше точность модели. О точности модели нельзя судить по одному значению ошибки прогноза. Например, если прогнозная оценка месячного уровня производства в июне совпала с фактическим значением, то это не является достаточным доказательством высокой точности модели. Надо учитывать, что хороший единичный прогноз может быть получен и по плохой модели, и наоборот. Следовательно, о качестве применяемых моделей можно судить лишь по совокупности сопоставлений прогнозных значений с фактическими.