Лекция продолжение Пролог Списки Операции со списками

Лекция (продолжение) Пролог. Списки. Операции со списками.

План 1. 2. 3. 4. 5. 2 Понятие списка Объявление списков Обработка списков Примеры программ обработки списков Поиск пути на графе.

Списки Определение: Список – структура, представляющая собой последовательность однотипных величин, длина которой может меняться в процессе выполнения программы. Одна из основных структур данных в Прологе. Элементы списка перенумерованы слева направо. Элементы списка записываются в квадратных 3 скобках [ ].

Примеры списков [2, 45, 23, -8, 1] – список целых чисел. [ «Бобик» , «Фунтик» , «Барбос» ] – список строк. [ ] – пустой список 4

Объявление списков 5 Список определяется знаком * после указания типа данных списка в разделе domains. Синтаксис: Имя домена списка = имя домена* Например: domains list 1 = integer* list 2 = char*

Списки обрабатываются с помощью рекурсии, поэтому понятию списка можно дать второе, рекурсивное, определение. Список – это структура, определяемая следующим образом: А) пустой список [ ] – это список; Б) [H|T] – список, если, T – список. Здесь H – это голова списка, T – хвост списка 6

Примеры записи списков [1|[2, 3, 4]]. Здесь 1 - это голова списка, [2, 3, 4] – хвост списка, который также является списком и может быть в свою очередь разделен на голову и хвост. 2. [1, 2, 3, 4] – явного указания на голову и хвост нет. 1 – голова списка по умолчанию, но можно головой списка определить [1, 2], указав это явно (см. 1) 1. 7

Представление списка. [1 | [2, 3, 4]] 1 [2, 3, 4] = [2 | [3, 4]] 2 [3, 4] = [3 | [4]] 3 [4] = [4 | [ ]] 4 8 []

Принцип работы со списками. «Если не можешь решить задачу для всего списка, реши ее для головы списка, а затем для хвоста» . Это означает, что на каждом шаге задаче решается для списка, длина которого на 1 меньше чем у предыдущего. 9

Рекурсивная программа обработки списка состоит из двух частей: 1. Факт, являющийся граничным условием, завершающим прямой ход рекурсии (правило для пустого списка или головы списка). 2. Рекурсивное правило, которое сводит операцию над списком к операциям над хвостом списка. 10

Основные задачи обработки списков 1. 2. 3. 4. 5. 6. 11 Определение длины списка Поиск элементов списка Разделение списка на части Слияние списков Сортировка списка Определение номера элемента или элемента по номеру

Пример 1. Определение длины списка. domains list = integer* predicates length (list, integer) clauses length( [ ], 0). length( [ _ | T ], N) : - length (T, M), N=M+1. goal length([1, 2, 3, 4, 5], 4). No length([1, 2, 3, 4, 5], X). X=5 12

Пример 2. Слияние списков domains list = integer* predicates append (list, list) clauses append( [ ], L, L). append( [ H | T ], L, [H | S]) : - append (T, L, S). goal 13 append([1, 3], [5, 7], X). X=[1, 3, 5, 7]

Пример 3. Определение принадлежности элемента списку. domains list = integer* predicates element (integer, list) clauses element ( X, [X | _ ]). element ( X, [ _ | T ]) : - element (X, T). goal element (4, [1, 3, 5, 7]). no element (X, [1, 3, 5, 7]). X=1, X=3, X=5, X=7 14

Пример 4. Сортировка списка методом вставки. Cначала упорядочим хвост, а затем вставим голову в нужное место хвоста. Пустой список – упорядочен. domains list = integer* predicates sort (list, list) insert (integer, list) 15

clauses sort ( [ ], [ ]). sort ( [ H | T ], S) : - sort (T, S 1), insert (H, S 1, S). insert (H, [ ], [H]). insert (H, [ Y | T ], [ H | S ]) : - H=Y, insert (H, T, S). goal sort ([7, 3, 12, 5], X). X=[3, 5, 7, 12] 16

Поиск всех решений для цели сразу. Рекурсия не позволяет искать все альтернативные решения для целевого утверждения. В случае необходимости поиска всех возможных решений и объединения их в одну структуру используется встроенный предикат: findall (Var. Name, my. Predicates, Listparam) 17

Предикат findall. Var. Name – имя переменной, определяет параметр, который необходимо собрать в список. my. Predicates – определяет предикат, из которого надо собрать значения. Listparam – список параметров. Содержит список значений, собранных методом поиска с возвратом. 18

Пример 5. Печать среднего возраста группы людей. domains name, address = string age = integer list = age* predicates person (name, address, age) sumlist (list, age, integer) clauses sumlist ([ ], 0, 0). sumlist ([H|T], Sum, N) : - sumlist (T, S 1, N 1), 19 Sum=H+S 1, N=1+N 1.

person (“Вика”, “Маркса 15”, 30). person (“Дмитрий”, “Комсомольский 45”, 48). person (“Анастасия”, “Вавилова 23”, 17). goal findall (Age, person (_, _, Age), L), sumlist (L, Sum, N), Ave=Sum/N, write (“Average=”, Ave), nl В этом примере предикат findall соберет в один список L все возрасты, которые есть в предикате person. 20

Решение задач, использующих структуру графа К этому типу относятся такие задачи как: Поиск выхода в лабиринте Поиск кратчайшего пути между двумя точками Задача обхода графа. Задачи поиска всех возможных путей. 21

Пример 6. Поиск пути на графе. Задание: нарисовать открытый конверт, не отрывая карандаша от бумаги. 1 a b 2 d 4 22 c f e h Определяем 2 множества: 1. Множество вершин. 2. Множество отрезков, соединяющих вершины. 3 Задача сводится к следующей: построить путь Р, в котором все q ребра различны и начало следующего является концом 5 предыдущего. База знаний – это список ребер.

Правило определения пути: way ( _ , P ) : - length (P, 8), writel (P). way ( H, P ) : - rebro (S, H, R), not (element (S, P)), way (R, [ S | P ]). 23

domains list = symbol* predicates length (list, integer) /*Длина пройденного пути*/ element (symbol, list) /*Является ли ребро элементом списка*/ writel (list) /*печать списка*/ way (integer, list) /*ищем путь от некоторой вершины в виде списка*/ rebro (symbol, integer) /*вершины, соединяющие ребро*/ 24

clauses rebro (a, 1, 2). rebro (a, 2, 1). rebro (b, 1, 3). rebro (b, 3, 1). rebro (c, 2, 3). rebro (c, 3, 2). rebro (d, 1, 4). rebro (d, 4, 1). rebro (e, 1, 5). rebro (e, 5, 1). rebro (f, 3, 4). rebro (f, 4, 3). rebro (g, 3, 5). rebro (g, 5, 3). rebro (h, 4, 5). rebro (h, 5, 4). 25

26 length ([ ], 0). /*Определение длины пути*/ length ([ _ | T], N) : - length (T, M), N=M+1. element (H, [ H | _ ]). /*Определение принадлежности элемента списку*/ element (H, [ _ | T ]) : - element (H, T). writel ([ ]). /*Печать списка*/ writel ([ H | T ]) : - writel (T), write (H). way (H, P) : - length (P, 8), writel (P). /*если длина списка 8, то печатаем список*/

way ( H, P ) : - rebro (S, H, R), not (element (S, P)), way (R, [ S | P ]). /*ищем ребро, начиная с вершины H, если это ребро не элемент списка пути Р, то добавим его к пути*/ goal way (4, [ ]). hуaсfdlg 27 way (1, [ ]). No

Примеры решения логических задач 28

Пример 1. Ханойские башни. Постановка задачи: В игре используется три стержня и набор из N дисков разного размера. Изначально все диски нанизаны на левый стержень в порядке убывания диаметра. Цель – переместить все диски на правый стержень, используя центральный как запасной. Условия: 1. Перемещать за один раз можно только один диск (верхний) 2. Нельзя класть диск на диск меньшего диаметра. 29

Стратегия решения 1. 2. Один диск перемещается непосредственно N дисков переносятся в 3 этапа: 1. 2. 3. 30 Перенести N-1 дисков на средний стержень Перенести последний диск на правый стержень Перенести N-1 дисков со среднего стержня на правый.

Используемые предикаты 1. 2. 31 Предикат hanoy (integer), показывающий со сколькими дисками идет игра. Предикат move, описывающий перенос N дисков с левого стержня на правый с промежуточным средним. Предикат inform, указывающий на действие с конкретным диском, вспомогательный для вывода пояснений.

Domains loc = right; middle, left Predicates hanoy (integer) move (integer, loc, loc) inform (loc, loc) Clauses hanoy(N) : - move (N, left, middle, right). 32 move (1, A, _ , C) : - inform (A, C), !.

move (N, A, B, C) : - M=N-1, move (M, A, C, B), inform (A, C), move (M, B, A, C). inform (Loc 1, Loc 2) : - nl, write (“Move a disk from ”, Loc 1, “ to ”, Loc 2). Goal hanoy (3) Результат: Move a disk from left to right Move a disk from left to middle Move a disk from right to middle 33 Move a disk from left to right

Move a disk from middle to left Move a disk from middle to right Move a disk from left to right yes 34

Пример 2. Задача о ферзях Постановка задачи: Расставить на шахматной доске 8 х8 восемь шахматных ферзей так, чтобы ни один из них угрожал другому. Построим модель. Перенумеруем ряды клеток, расположенных по горизонтали и вертикали от 1 до 8. Для нумерации диагоналей поделим их на два типа: Diagonal=8+Column-Row (тип 1) Diagonal=Row+Column-1 (тип 2) Для примера перенумеруем клетки квадрата 4 х4 35

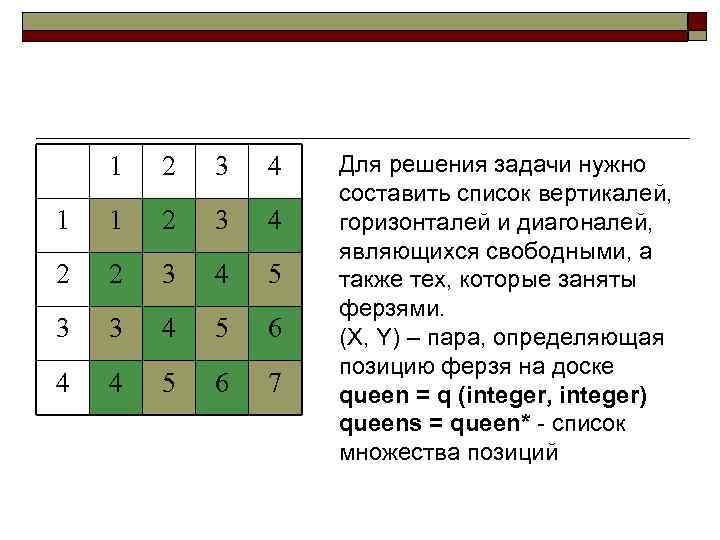1 3 4 1 1 2 3 4 2 2 3 4 5 3 3 4 5 6 4 36 2 4 5 6 7 Для решения задачи нужно составить список вертикалей, горизонталей и диагоналей, являющихся свободными, а также тех, которые заняты ферзями. (X, Y) – пара, определяющая позицию ферзя на доске queen = q (integer, integer) queens = queen* - список множества позиций

freelist = integer* - списки свободных вертикалей, горизонталей и диагоналей. Шахматную доску опишем как единый объект: board = board (queens, freelist, freelist) Для примера: пустая доска 4 х4: board ([], [1, 2, 3, 4], [1, 2, 3, 4, 5, 6, 7]) доска с одним ферзем: board ([1, 1], [2, 3, 4], [2, 3, 4, 5, 6, 7]) 37

Ферзи размещаются по одному до тех пор, пока не будут заняты все вертикали, горизонтали и диагонали. Введем предикат place. N (integer, board), для которого опишем правила. Списки вертикалей и горизонталей пусты place. N(_, board(D, [ ], X, Y)) : -!. Связь между двумя расстановками при добавлении ферзя: place. N (N, Board 1, Result) : - place_a_queen(N, 38 Board 1, Board 2), place. N (N, Board 2, Result).

place_a_queen (integer, board) Нового ферзя добавляем к списку стоящих на доске ферзей. Среди свободных горизонталей ищем ту, на которую можно поставить нового ферзя и удалить ее из списка свободных горизонталей. findandremove (R, Rows, New. R) Аналогично действуем для вертикалей с переменной С. С помощью R и C вычислим диагонали и будем искать их в списках 39 свободных диагоналей.

Листинг программы domains queen = q (integer, integer) queens = queen* freelist = integer* board = board (queens, freelist, freelist) predicates place. N (integer, board) place_a_queen (integer, board) nqueens (integer) makelist (integer, freelist) findandremove (integer, freelist) 40 nextrow (integer, freelist)

clauses nqueens (N) : - makelist (N, L), Diagonal=N*2 -1, makelist (Diagonal, LL), place. N (N, board([], L, L, LL), Final), write (Final). place. N(_, board(D, [], [], D 1, D 2)) : -!. place. N (N, Board 1, Result) : - place_a_queen(N, Board 1, Board 2), place. N (N, Board 2, Result). place_a_queen (N, board(Queens, Rows, Columns, Diag 1, Diag 2), board([q(R, C)|Queens], New. R, New. C, New. D 1, New. D 2)) : nextrow (R, Rows, New. R), findandremove (C, Columns, New. C), D 1=N+C-R, findandremove (D 1, Diag 1, New. D 1), 41 D 2=R+C-1, findandremove (D 2, Diag 2, New. D 2).

findandremove (X, [X | Rest], Rest). findandremove (X, [Y | Rest], [Y | Tail]) : findandremove (X, Rest, Tail). makelist (1, [1]). makelist (N, [N | Rest]) : - N 1=N-1, makelist (N 1, Rest). nextrow (Row, [Row | Rest], Rest). goal nqueens(5), nl, readchar (_). 42