Скачать презентацию Лекция по дисциплине Криптография и Скачать презентацию Лекция по дисциплине Криптография и

ПОТОКОВЫЕ ШИФРЫ 3 (Лекция 8 ТЗит).ppt

  • Количество слайдов: 26

. • Лекция по дисциплине «Криптография и стеганография» . • Лекция по дисциплине «Криптография и стеганография»

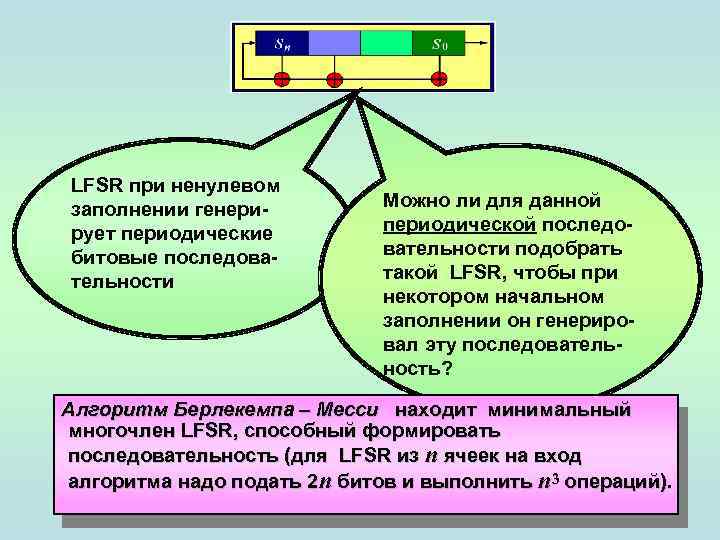LFSR при ненулевом заполнении генерирует периодические битовые последовательности Можно ли для данной периодической LFSR при ненулевом заполнении генерирует периодические битовые последовательности Можно ли для данной периодической последовательности подобрать такой LFSR, чтобы при некотором начальном заполнении он генерировал эту последовательность? Алгоритм Берлекемпа – Месси находит минимальный многочлен LFSR, способный формировать последовательность (для LFSR из n ячеек на вход алгоритма надо подать 2 n битов и выполнить n 3 операций).

Линейная сложность последовательности – степень ее минимального многочлена Последовательность – бесконечна 1. 2. Нет Линейная сложность последовательности – степень ее минимального многочлена Последовательность – бесконечна 1. 2. Нет LFSR, генерирующего последовательность 3. длина самого короткого регистра, который генерирует последовательность Последовательность – конечна длина самого короткого LFSR, порождающего по следовательность, первые члены которой есть Определяется с помощью алгоритма Берлекемпа - Месси

Свойства линейной сложности последовательностей • если • • если битовые последовательности, то НОД где Свойства линейной сложности последовательностей • если • • если битовые последовательности, то НОД где периоды последовательностей; • достигает максимума при НОД • если минимальный многочлен LFSR – примитивный многочлен степени над полем GF(2), то каждое ненулевое начальное заполнение дает на выходе последовательность со сложностью .

Какова линейная сложность последовательности ? • Можно ли ее выбрать на роль гаммы потокового Какова линейная сложность последовательности ? • Можно ли ее выбрать на роль гаммы потокового шифра? • Высокая линейная сложность гаммы – необходимое, но недостаточное условие для выбора последовательности на роль гаммы потокового шифра!!! • Для определения зависимости линейной сложности от длины последовательности в 80 -х гг. ХХ ст. швейцарский криптограф Райнер Рюппель ввел профиль линейной сложности.

Пусть – линейная сложность первых членов бесконечной битовой последовательности. Тогда ряд чисел называется Пусть – линейная сложность первых членов бесконечной битовой последовательности. Тогда ряд чисел называется профилем линейной сложности последовательности. Свойства профиля линейной сложности: 1. Если , то 2. , если 3. Если то 4. Профиль линейной сложности истинно случайных последовательностей неограниченно приближается к прямой иначе последовательность – неслучайна.

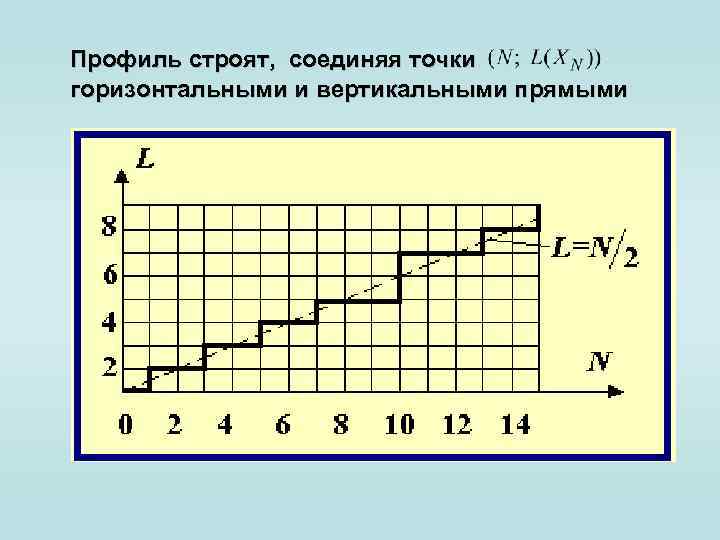Профиль строят, соединяя точки горизонтальными и вертикальными прямыми Профиль строят, соединяя точки горизонтальными и вертикальными прямыми

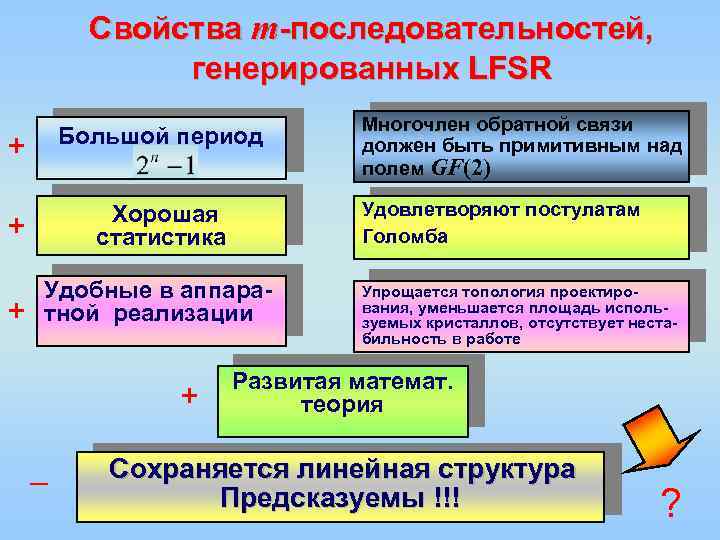Свойства m-последовательностей, генерированных LFSR + Большой период + Хорошая статистика + Удобные в аппаратной Свойства m-последовательностей, генерированных LFSR + Большой период + Хорошая статистика + Удобные в аппаратной реализации + – Многочлен обратной связи должен быть примитивным над полем GF(2) Удовлетворяют постулатам Голомба Упрощается топология проектирования, уменьшается площадь используемых кристаллов, отсутствует нестабильность в работе Развитая математ. теория Сохраняется линейная структура Предсказуемы !!! ?

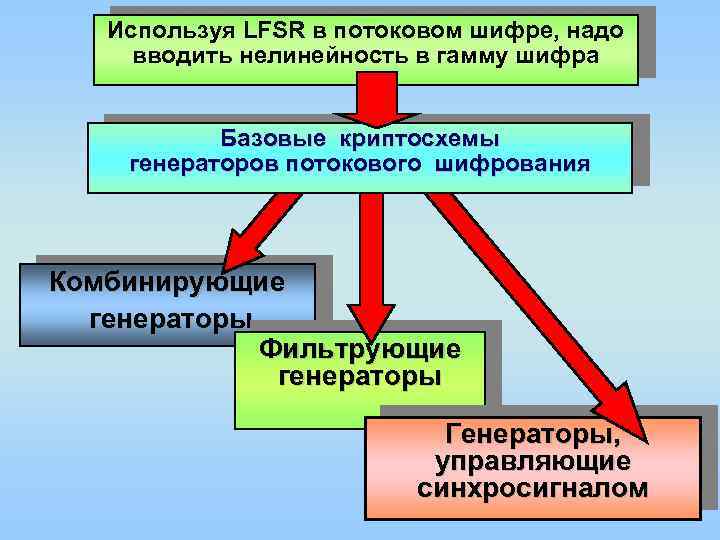Используя LFSR в потоковом шифре, надо вводить нелинейность в гамму шифра . Базовые криптосхемы Используя LFSR в потоковом шифре, надо вводить нелинейность в гамму шифра . Базовые криптосхемы генераторов потокового шифрования Комбинирующие генераторы Фильтрующие генераторы Генераторы, управляющие синхросигналом

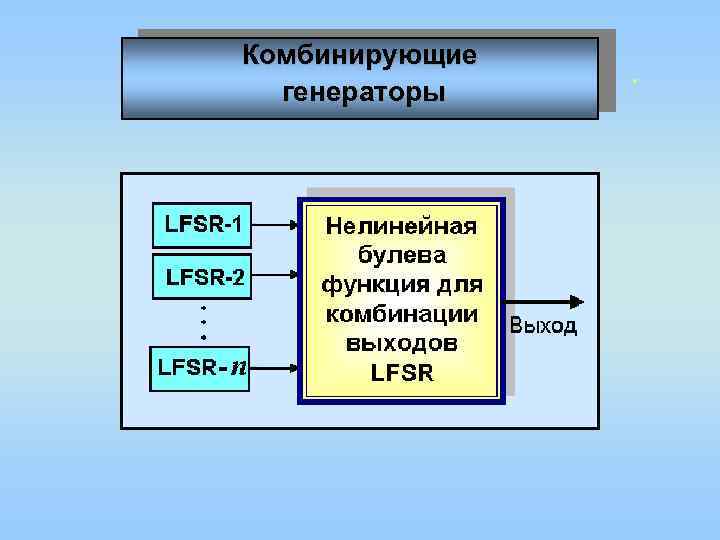Комбинирующие . генераторы Комбинирующие . генераторы

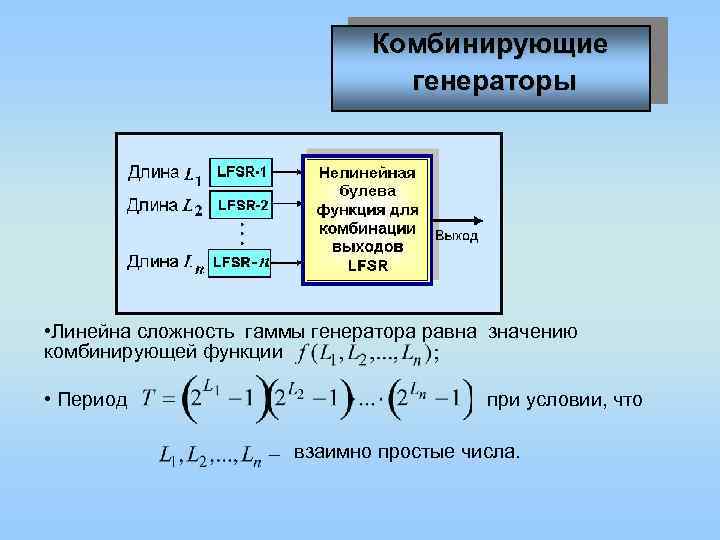Комбинирующие генераторы • Линейна сложность гаммы генератора равна значению комбинирующей функции • Период при Комбинирующие генераторы • Линейна сложность гаммы генератора равна значению комбинирующей функции • Период при условии, что взаимно простые числа.

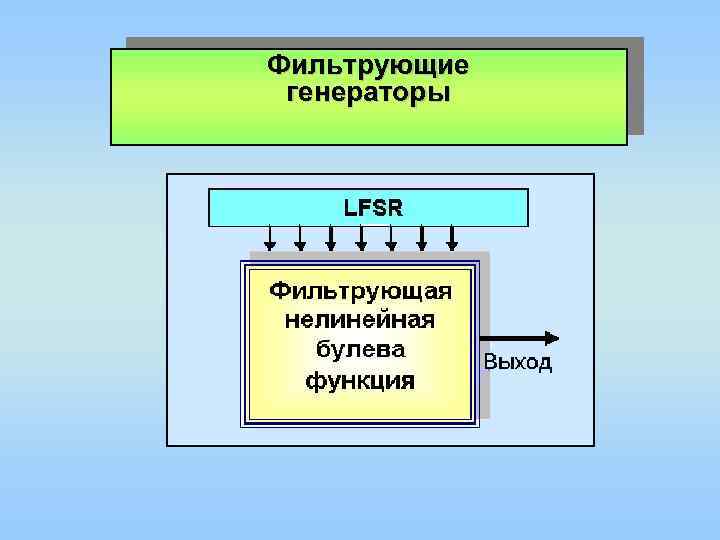Фильтрующие генераторы Фильтрующие генераторы

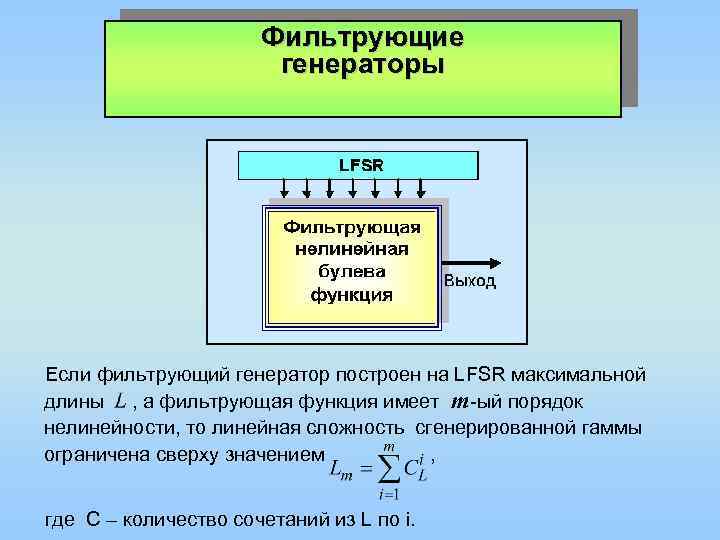Фильтрующие генераторы Если фильтрующий генератор построен на LFSR максимальной длины , а фильтрующая функция Фильтрующие генераторы Если фильтрующий генератор построен на LFSR максимальной длины , а фильтрующая функция имеет т-ый порядок нелинейности, то линейная сложность сгенерированной гаммы ограничена сверху значением , где С – количество сочетаний из L по i.

Генераторы, управляющие синхросигналом Генераторы переменного шага ( «stop and go» ) Сжимающие генераторы Генераторы, управляющие синхросигналом Генераторы переменного шага ( «stop and go» ) Сжимающие генераторы

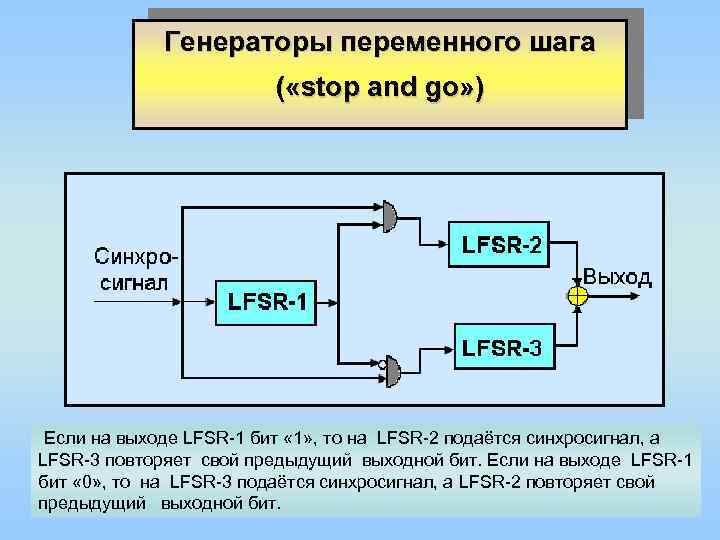Генераторы переменного шага ( «stop and go» ) Если на выходе LFSR-1 бит « Генераторы переменного шага ( «stop and go» ) Если на выходе LFSR-1 бит « 1» , то на LFSR-2 подаётся синхросигнал, а LFSR-3 повторяет свой предыдущий выходной бит. Если на выходе LFSR-1 бит « 0» , то на LFSR-3 подаётся синхросигнал, а LFSR-2 повторяет свой предыдущий выходной бит.

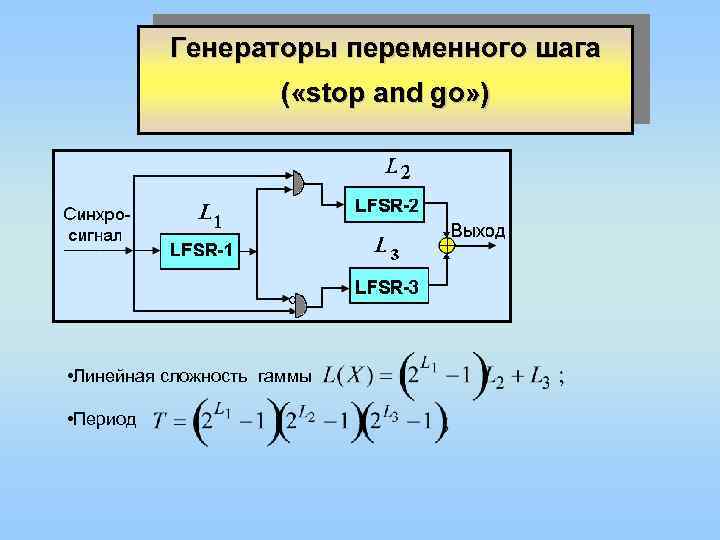Генераторы переменного шага ( «stop and go» ) • Линейная сложность гаммы • Период Генераторы переменного шага ( «stop and go» ) • Линейная сложность гаммы • Период

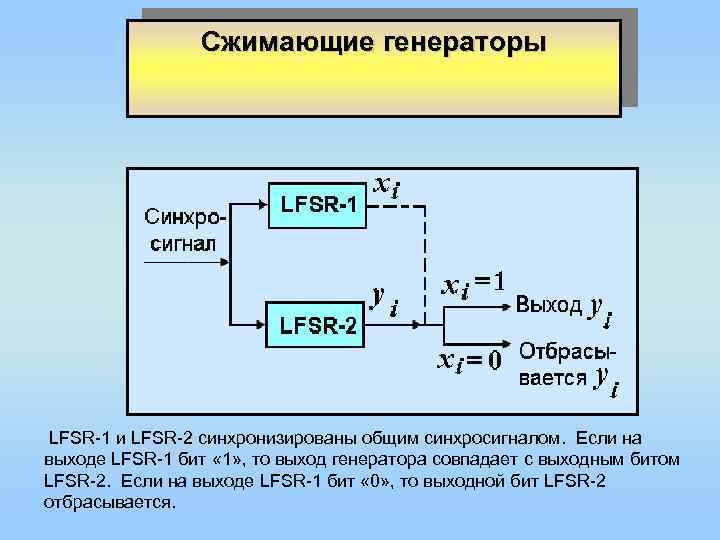Сжимающие генераторы LFSR-1 и LFSR-2 синхронизированы общим синхросигналом. Если на выходе LFSR-1 бит « Сжимающие генераторы LFSR-1 и LFSR-2 синхронизированы общим синхросигналом. Если на выходе LFSR-1 бит « 1» , то выход генератора совпадает с выходным битом LFSR-2. Если на выходе LFSR-1 бит « 0» , то выходной бит LFSR-2 отбрасывается.

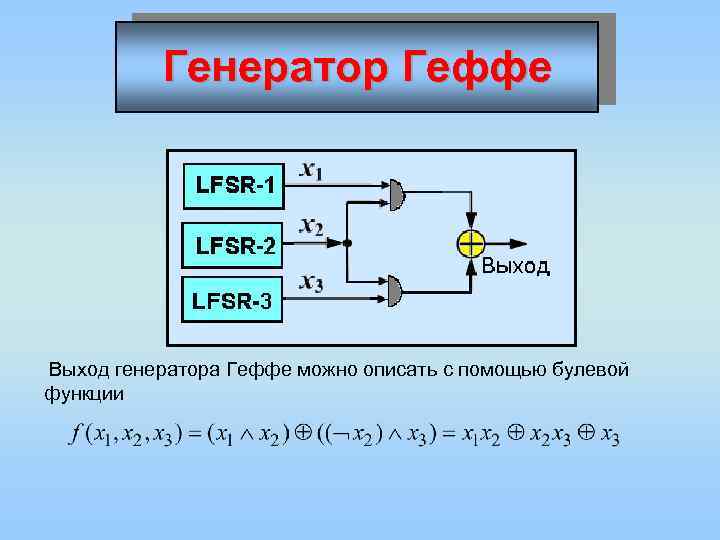Генератор Геффе Выход генератора Геффе можно описать с помощью булевой функции Генератор Геффе Выход генератора Геффе можно описать с помощью булевой функции

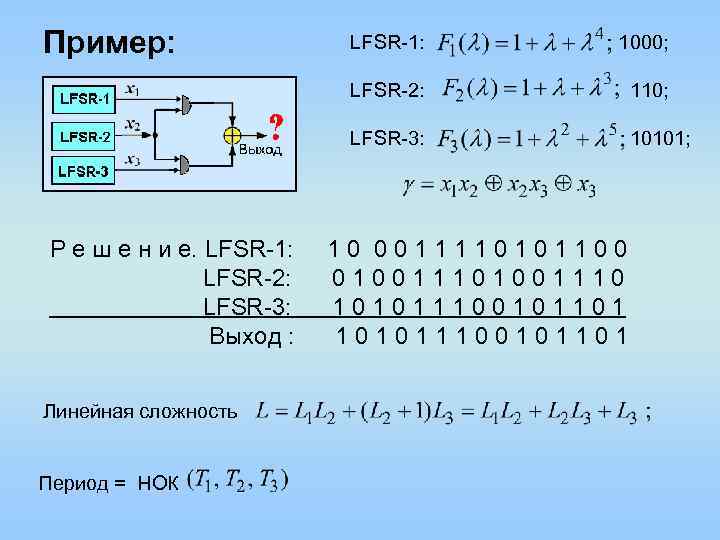Пример: LFSR-1: 1000; LFSR-2: 110; LFSR-3: 10101; Р е ш е н и е. Пример: LFSR-1: 1000; LFSR-2: 110; LFSR-3: 10101; Р е ш е н и е. LFSR-1: 1 0 0 0 1 1 0 0 LFSR-2: 0 1 0 0 1 1 1 0 LFSR-3: 1 0 1 1 1 0 0 1 1 0 1 Выход : 1 0 1 1 1 0 0 1 1 0 1 Линейная сложность Период = НОК

Криптоанализ генератора Геффе выходящие биты трех LFSR и выходной последовательности генератора соответственно Криптоанализ генератора Геффе выходящие биты трех LFSR и выходной последовательности генератора соответственно

Генератор BBS Назван по первым буквам авторов Леоноры Блюм, Мануэля Блюма и Майкла Шуб Генератор BBS Назван по первым буквам авторов Леоноры Блюм, Мануэля Блюма и Майкла Шуб (англ. Blum – Shub)

Генератор BBS 1. 2. 3. 4. Выбрать случайно два больших простых числа p и Генератор BBS 1. 2. 3. 4. Выбрать случайно два больших простых числа p и q, для которых ; Найти n=pq; Выбрать число ; НОД ; Вычислить число – начальное значение генератора; 5. Вычислить ; 6. Псевдослучайная битовая последовательность – это младшие биты чисел .

Пример: Найти выходную последовательность генератора BBS , если p=31, q =43. • n=pq=1333; х=919; Пример: Найти выходную последовательность генератора BBS , если p=31, q =43. • n=pq=1333; х=919; НОД(n; х)=1 • • • На выходе генератора 0 1 0 0 1 1 1. . . …

Результаты прохождения графического теста для последовательности BBSn(x 0) последовательности Распределение на плоскости Результаты прохождения графического теста для последовательности BBSn(x 0) последовательности Распределение на плоскости

Вольный пересказ старой газетной статьи. Шпион статьи. несколько раз прикурил, фотографируя спрятанным в зажигалке Вольный пересказ старой газетной статьи. Шпион статьи. несколько раз прикурил, фотографируя спрятанным в зажигалке фотоаппаратом открытую шифровальную машину с разных сторон. Затем, введя ключ из одних пробелов, он несколько сот раз нажал букву «А» . Полученная перфолента шифровки после внимательного рассмотрения была свернута в рулон и незаметно отправлена в карман. • Теперь вопрос: почему шпиона заинтересовала шифровка дурацкого текста из одной повторяющейся буквы?