Лекция N 12 Лектор:

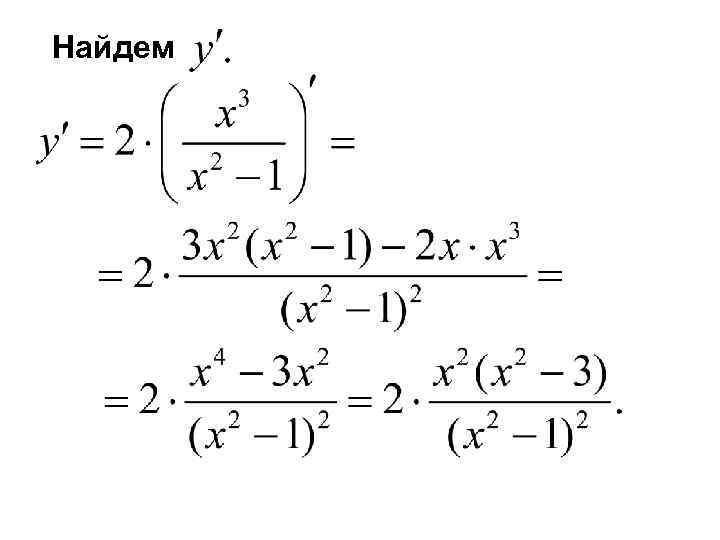
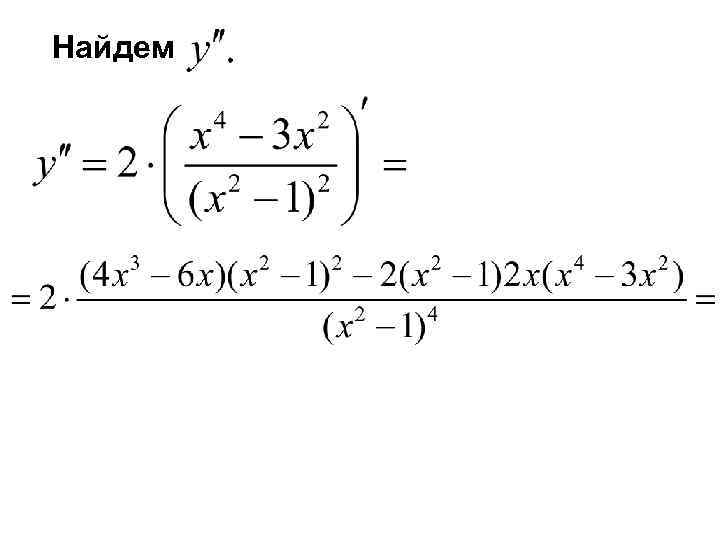
Лекция N 12 Лектор: доц. Лаптева Надежда Александровна Тема: Дифференциал функции. Исследование функции с помощью производной

Дифференциал функции Рассмотрим функцию Найдем

Приращение функции можно рассматривать как сумму двух слагаемых: - линейное относительно - нелинейное относительно

При оба слагаемых стремятся к нулю, но второе слагаемое быстрее стремится к нулю. Поэтому при малых считают, что (т. е. считают, что приближенно равно линейной части). Эту часть называют главной частью приращения функции или дифференциалом. Дифференциал функции обозначают

Теорема. Если функция имеет в точке дифференциал, то она имеет в этой точке производную и наоборот, если функция имеет в точке производную, то она имеет в этой точке дифференциал. Выражение для дифференциала записывается в форме

Примеры. Найти дифференциалы функций 1) 2)

Связь между дифференцируемостью и непрерывностью функции Теорема. Если функция дифференцируема в точке то она в этой точке непрерывна. Обратная теорема неверна: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми.

Пример. В точке функция непрерывна, так как

Справа от нуля поэтому Слева от нуля поэтому

Таким образом, отношение при справа и слева имеет различные пределы, а это значит, что при это отношение предела не имеет, т. е. производная в точке не существует.

Схема исследования функции 1) Найти область определения функции 2) Исследовать функцию на четность и нечетность 3) Найти точки пересечения с осями координат

4) Найти асимптоты кривой 5) Исследовать функцию по знаку первой производной , т. е. найти интервалы возрастания, убывания, точки экстремума

6) Исследовать функцию по знаку второй производной , т. е. найти интервалы выпуклости, вогнутости, точки перегиба 7) Построить график. Для построения графика можно все результаты исследования свести в таблицу.

Пример. Исследовать функцию и построить график: 1) Область определения:

2) Чётность, нечётность. четная, если нечетная, если функция нечетная, следовательно график функции симметричен относительно начала координат.

3) Точки пересечения с осями координат 4) Асимптоты – это прямые, к которым стремится график функции при неограниченном удалении от начала координат.

Асимптоты бывают: a) вертикальные. Они параллельны оси Уравнение вертикальной асимптоты b) наклонные. Уравнение где

c) если то и наклонная асимптота становится горизонтальной, т. е. параллельной оси Найдем асимптоты кривой Т. к. то - вертикальная асимптота.

Аналогично, - вертикальная асимптота. Заметим, что кривая может иметь сколько угодно вертикальных асимптот. Пример. Вертикальные асимптоты где

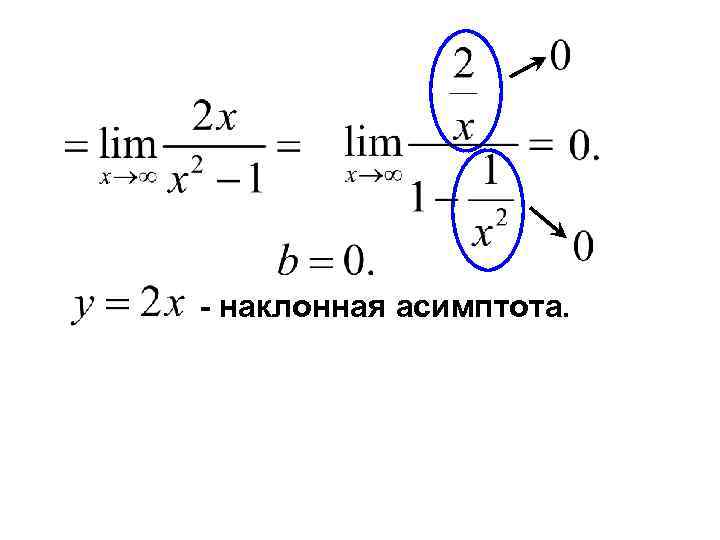
Найдем наклонную асимптоту

- наклонная асимптота.

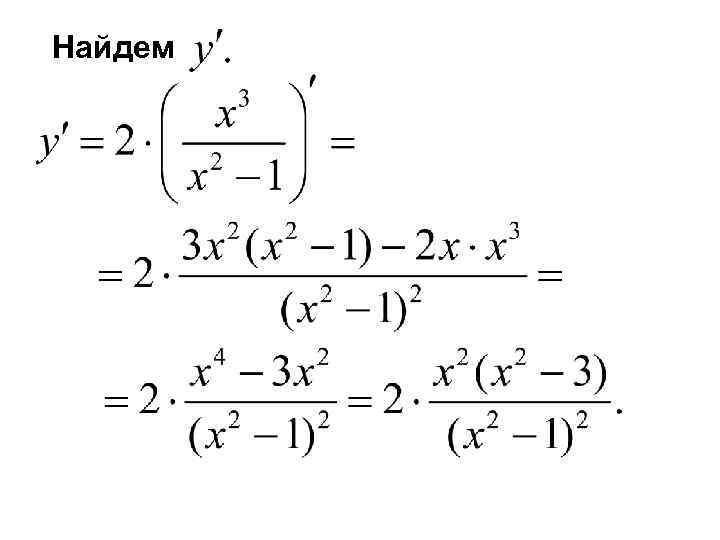Найдем

+ - - + - точка максимума. - точка минимума.

Можно было не рассматривать т. е. функция нечетная и достаточно построить график только для а затем отобразить график симметрично относительно начала координат.

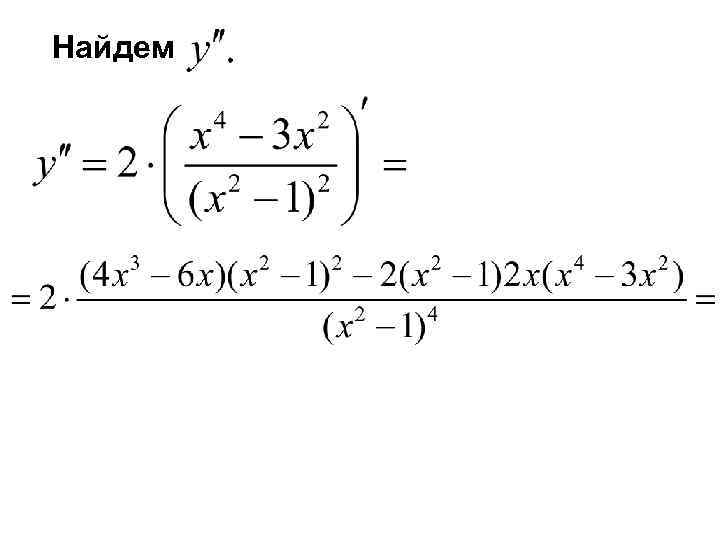Найдем

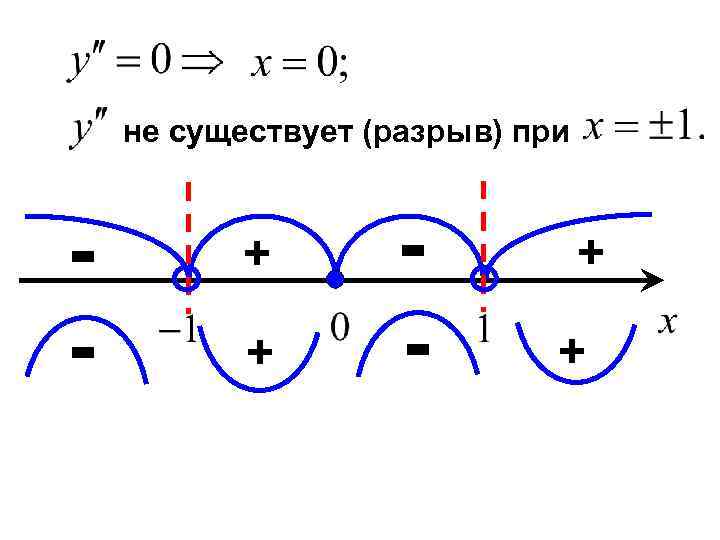
не существует (разрыв) при - +

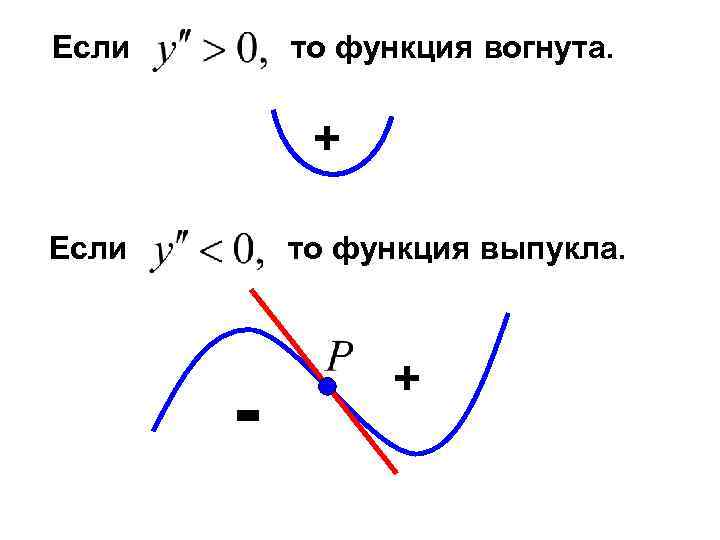
Если то функция вогнута. + Если то функция выпукла. + -

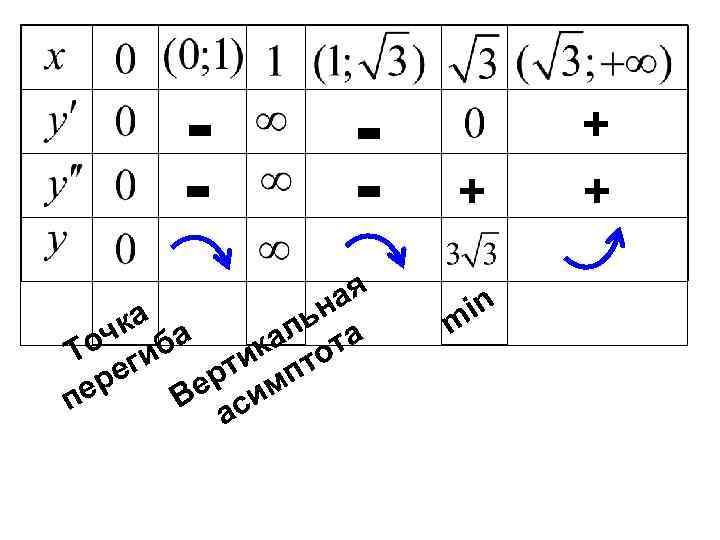
Точки, в которых выпуклость меняется на вогнутость или наоборот, называются точками перегиба. - точка перегиба. 7) Для построения графика сделаем сводную таблицу. Т. к. функция нечетная, то будем рассматривать только

- - + + ая in а чк ба ьн m о и ал ота Т г ик пт ер е рт м п Ве си а

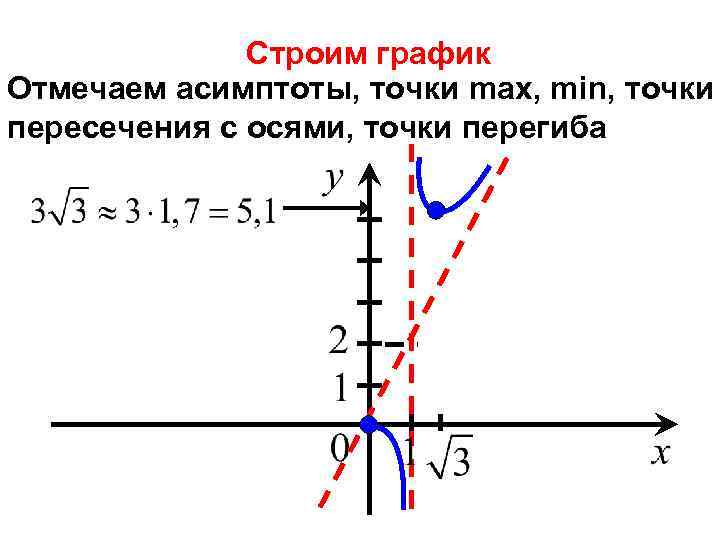
Строим график Отмечаем асимптоты, точки max, min, точки пересечения с осями, точки перегиба

Для строим график, используя нечетность функции.