ЛЕКЦИЯ Матрицы определители системы линейных уравнений Основные

ЛЕКЦИЯ Матрицы, определители, системы линейных уравнений

Основные определения

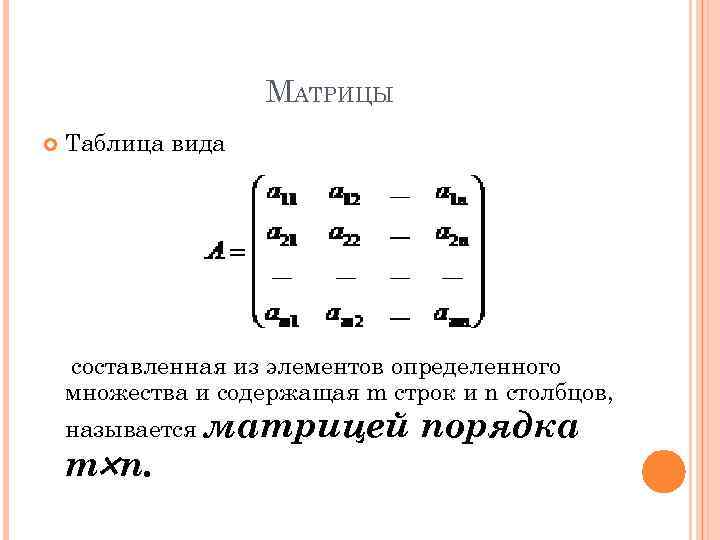МАТРИЦЫ Таблица вида составленная из элементов определенного множества и содержащая m строк и n столбцов, называется матрицей m n. порядка

РАВНЫЕ МАТРИЦЫ КВАДРАТНЫЕ МАТРИЦЫ Квадратная матрица 2 -го порядка Квадратная матрица 3 -го порядка

ГЛАВНАЯ И ПОБОЧНАЯ ДИАГОНАЛИ Главная диагональ состоит из нулевых элементов Побочная диагональ состоит их единичных элементов

ДИАГОНАЛЬНЫЕ И ЕДИНИЧНЫЕ МАТРИЦЫ Диагональные матрицы Единичные матрицы

ТРЕУГОЛЬНЫЕ МАТРИЦЫ Матрица А наз. треугольная сверху Матрица В наз. треугольная снизу

«ИНТЕРЕСНЫЕ» МАТРИЦЫ Вектор-столбец Вектор-строка

Операции над матрицами

СЛОЖЕНИЕ МАТРИЦ Сложение матриц обладает следующими свойствами: 1) коммутативность: А+В = В+А; 2) ассоциативность: (А+В)+С = А+(В+С).

УМНОЖЕНИЕ МАТРИЦЫ НА ЧИСЛО Умножение матрицы на число обладает следующими свойствами: 1) ассоциативность относительно числового множителя: ( )A = ( A); 2) дистрибутивность относительно суммы матриц: (A+B)= A+ B; 3) дистрибутивность относительно суммы чисел: ( + )A= A+ A.

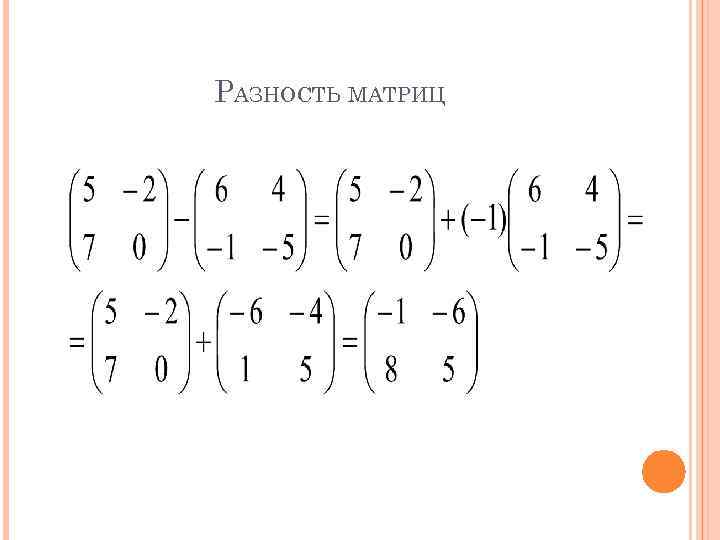РАЗНОСТЬ МАТРИЦ

УМНОЖЕНИЕ МАТРИЦ Произведение матриц обладает следующими свойствами: 1) ассоциативность: (АВ)С=А(ВС); 2) дистрибутивность относительно суммы матриц: А(В+С)=АВ+АС.

ЗАМЕЧАНИЯ Если А и В квадратные матрицы одного размера, то произведение A B и B A всегда существуют. Матрицы А и В называются перестановочными, если А В = В А. Кроме этого, А Е = Е А = А, где А - квадратная матрица, Е - единичная матрица того же размера.

ТРАНСПОНИРОВАНИЕ МАТРИЦ Пример Транспонированная матрица обладает следующими свойствами: 1) Дважды транспонированная матрица равна исходной матрице: (АТ)Т=А. 2) При транспонировании квадратных матриц элементы, находящиеся на главной диагонали, не меняют своих позиций. 3) Симметричная матрица не изменяется при транспонировании.

ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ Перестановка строк, а затем столбцов Элементы второй строки получены сложением элементов первой и второй строк

Определители матрицы

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Если порядок матрицы n=1, то есть A=(a 11), тогда det. A=ΔA=a 11 Если порядок матрицы n=2, то есть тогда det. A=ΔА=

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Если порядок матрицы n=3, то есть Тогда

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ

ОБРАТНАЯ МАТРИЦА

ОБРАТНАЯ МАТРИЦА

РАНГ МАТРИЦЫ

РАНГ МАТРИЦЫ Из определения ранга матрицы следуют его свойства: rang. A≤min(m; n), то есть ранг матрицы не превосходит меньшего из ее размеров. rang. A=0 тогда и только тогда, когда А – нулевая матрица. Ранг матрицы не изменится, если из нее вычеркнуть все нулевые строки и столбцы. Ранг матрицы не изменится при ее транспонировании. Элементарные преобразования матрицы не меняют ее ранга

Системы линейных уравнений и методы их решения

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ОБРАТНОЙ МАТРИЦЫ

РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ОБРАТНОЙ МАТРИЦЫ

РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ОБРАТНОЙ МАТРИЦЫ

РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ОБРАТНОЙ МАТРИЦЫ

РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ОБРАТНОЙ МАТРИЦЫ

РЕШЕНИЕ СЛАУ МЕТОДОМ КРАМЕРА

РЕШЕНИЕ СЛАУ МЕТОДОМ КРАМЕРА

РЕШЕНИЕ СЛАУ МЕТОДОМ ГАУССА

РЕШЕНИЕ СЛАУ МЕТОДОМ ГАУССА Прибавив ко второй строке первую, умноженную на (-2), к третьей - первую, умноженную на (-3), к четвертой – первую, умноженную на (-1), получим

РЕШЕНИЕ СЛАУ МЕТОДОМ ГАУССА Разделим третью строку на 13 и поменяем местами вторую и третью строки Прибавим к 3 -й строке 2 -ю, умноженную на (-9), и к четвертой вторую, умноженную на (-2), получим

РЕШЕНИЕ СЛАУ МЕТОДОМ ГАУССА Разделим 3 -ю строку на (-2), а четвертую на (-7), тогда Этой матрице соответствует система