ЛЕКЦИЯ Функция дифференцирование и интегрирование функций Дифференциальные уравнения

ЛЕКЦИЯ Функция, дифференцирование и интегрирование функций. Дифференциальные уравнения

ПОНЯТИЕ ФУНКЦИИ Если каждому элементу х множества Х по определенному правилу можно поставить в соответствие одно или несколько значений элемента у множества У, то говорят, что задана функция y от x y=f(x) Совокупность значений x для которых правило вычисления значений y имеет смысл, называется областью определения функции, а область изменения У называется множеством значений функции.

СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ Табличный способ задания функции. При этом способе выписываются в определенном порядке значения аргумента и соответствующие им значения функции. Примером таких таблиц могут служить таблицы тригонометрических функций, таблицы логарифмов. Х 1 2 … … n У У(1) У(2) … … У(n)

СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ Графический способ задания функции. Если в прямоугольной системе координат на плоскости изобразить в виде линии некоторую совокупность точек с координатами (х, у), где y=f(x), то получим график функции. 6 4 2 0 Ряд 1. . . ат е К К ат е . . . Ряд 2 Ряд 3

СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ Аналитический способ задания функции. В этом способе функция представлена аналитическим выражением, то есть через совокупность математических операций, которые производятся в определенной последовательности над числами и символами. Например: y=5 ln(x) или f(x)=x 2 -9

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 18 16 Y 14 12 10 8 6 4 2 0 1 -2 2 3 X 4 5

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ

ПЕРИОДИЧНОСТЬ ФУНКЦИИ

ВОЗРАСТАЮЩИЕ/УБЫВАЮЩИЕ ФУНКЦИИ

ПРЕДЕЛ ФУНКЦИИ

СЛОЖНАЯ ФУНКЦИИ

ПРОИЗВОДНАЯ ФУНКЦИИ

ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

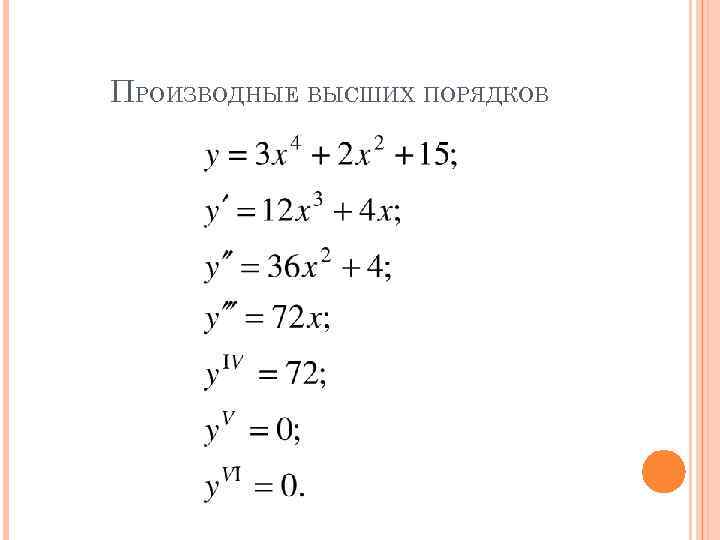ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ

ДИФФЕРЕНЦИАЛ ФУНКЦИИ

ПЕРВООБРАЗНАЯ ФУНКЦИИ

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА

МЕТОДЫ ИНТЕГРИРОВАНИЯ

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

НАХОЖДЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА Формула Ньютона. Лейбница

СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

МЕТОДЫ ИНТЕГРИРОВАНИЯ И ПРИМЕНЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

ПРОСТЕЙШЕЕ ДУ

ДУ С РАЗДЕЛЯЮЩИМИ ПЕРЕМЕННЫМИ

ДУ С РАЗДЕЛЯЮЩИМИ ПЕРЕМЕННЫМИ

ДУ С РАЗДЕЛЯЮЩИМИ ПЕРЕМЕННЫМИ