Фотограмметрия_Л9.pptx
- Количество слайдов: 24
 Лекция № 9 ТЕОРИЯ ПАРЫ СНИМКОВ
Лекция № 9 ТЕОРИЯ ПАРЫ СНИМКОВ
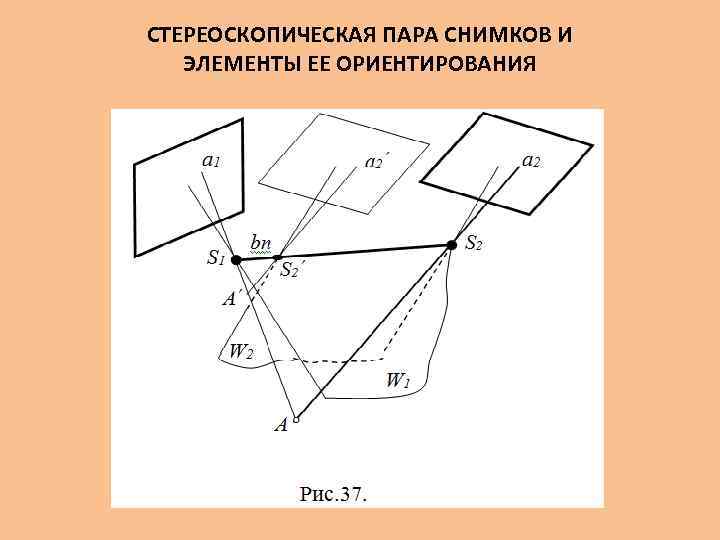
 СТЕРЕОСКОПИЧЕСКАЯ ПАРА СНИМКОВ И ЭЛЕМЕНТЫ ЕЕ ОРИЕНТИРОВАНИЯ Два снимка с изображениями одного и того же участка местности, полученные с двух точек пространства, называются стереоскопической парой снимков (стереопарой). Снимок, полученный с точки фотографирования S 1, называется левым, а с S 2 – правым. На рис. 37 изображена пара снимков в положении, которое она занимала в момент фотографирования. А – точка местности, изобразившаяся на снимках в точках а 1 и а 2. Они называются соответственными или одноимёнными точками. Проектирующие лучи S 1 A и S 2 A, проходящие через эти точки называются соответственными или одноимёнными проектирующими лучами.
СТЕРЕОСКОПИЧЕСКАЯ ПАРА СНИМКОВ И ЭЛЕМЕНТЫ ЕЕ ОРИЕНТИРОВАНИЯ Два снимка с изображениями одного и того же участка местности, полученные с двух точек пространства, называются стереоскопической парой снимков (стереопарой). Снимок, полученный с точки фотографирования S 1, называется левым, а с S 2 – правым. На рис. 37 изображена пара снимков в положении, которое она занимала в момент фотографирования. А – точка местности, изобразившаяся на снимках в точках а 1 и а 2. Они называются соответственными или одноимёнными точками. Проектирующие лучи S 1 A и S 2 A, проходящие через эти точки называются соответственными или одноимёнными проектирующими лучами.
 СТЕРЕОСКОПИЧЕСКАЯ ПАРА СНИМКОВ И ЭЛЕМЕНТЫ ЕЕ ОРИЕНТИРОВАНИЯ
СТЕРЕОСКОПИЧЕСКАЯ ПАРА СНИМКОВ И ЭЛЕМЕНТЫ ЕЕ ОРИЕНТИРОВАНИЯ
 СТЕРЕОСКОПИЧЕСКАЯ ПАРА СНИМКОВ И ЭЛЕМЕНТЫ ЕЕ ОРИЕНТИРОВАНИЯ
СТЕРЕОСКОПИЧЕСКАЯ ПАРА СНИМКОВ И ЭЛЕМЕНТЫ ЕЕ ОРИЕНТИРОВАНИЯ
 Представим теперь, что одна из связок (например, правая) поступательно перемещается вдоль базиса из положения S 2 в S 2. Модель при этом не разрушится, но изменится ее масштаб. Расстояние bп между центрами проекций двух связок, по которым построена модель, называется базисом проектирования, и ее масштаб вычисляется по формуле: (62) Существует понятие элементы ориентирования стереопары. К ним относят рассмотренные ранее элементы ориентирования (внутреннего x 0, y 0, f и внешнего XS, YS, ZS, α, ω, и κ) каждого из образующих ее снимков, таким образом, общее их число 18. Другую тройку угловых элементов внешнего ориентирования снимков на практике также используют, но значительно реже.
Представим теперь, что одна из связок (например, правая) поступательно перемещается вдоль базиса из положения S 2 в S 2. Модель при этом не разрушится, но изменится ее масштаб. Расстояние bп между центрами проекций двух связок, по которым построена модель, называется базисом проектирования, и ее масштаб вычисляется по формуле: (62) Существует понятие элементы ориентирования стереопары. К ним относят рассмотренные ранее элементы ориентирования (внутреннего x 0, y 0, f и внешнего XS, YS, ZS, α, ω, и κ) каждого из образующих ее снимков, таким образом, общее их число 18. Другую тройку угловых элементов внешнего ориентирования снимков на практике также используют, но значительно реже.
 ЗАВИСИМОСТЬ МЕЖДУ КООРДИНИТАМИ ТОЧКИ МЕСТНОСТИ И КООРДИНАТАМИ ЕЕ ИЗОБРАЖЕНИЯ НА ПАРЕ СНИМКОВ
ЗАВИСИМОСТЬ МЕЖДУ КООРДИНИТАМИ ТОЧКИ МЕСТНОСТИ И КООРДИНАТАМИ ЕЕ ИЗОБРАЖЕНИЯ НА ПАРЕ СНИМКОВ
 ЗАВИСИМОСТЬ МЕЖДУ КООРДИНИТАМИ ТОЧКИ МЕСТНОСТИ И КООРДИНАТАМИ ЕЕ ИЗОБРАЖЕНИЯ НА ПАРЕ СНИМКОВ
ЗАВИСИМОСТЬ МЕЖДУ КООРДИНИТАМИ ТОЧКИ МЕСТНОСТИ И КООРДИНАТАМИ ЕЕ ИЗОБРАЖЕНИЯ НА ПАРЕ СНИМКОВ
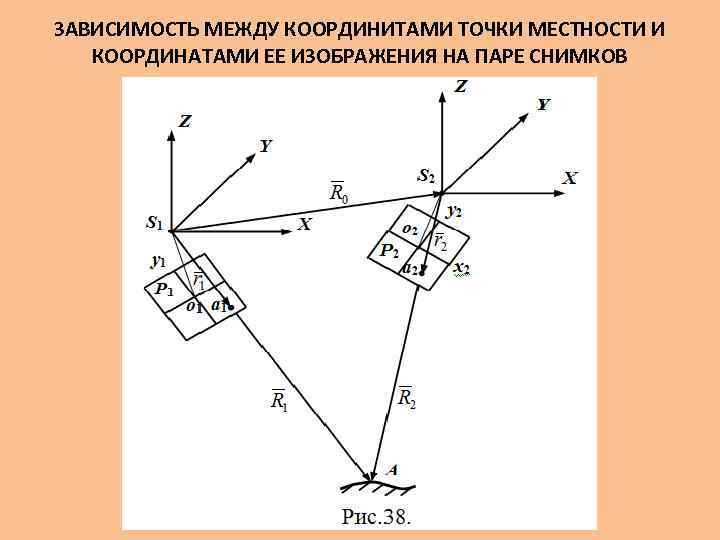
 ЗАВИСИМОСТЬ МЕЖДУ КООРДИНИТАМИ ТОЧКИ МЕСТНОСТИ И КООРДИНАТАМИ ЕЕ ИЗОБРАЖЕНИЯ НА ПАРЕ СНИМКОВ Задача определения пространственных координат точки местности по её изображению на снимках стереопары называется прямой пространственной фотограмметрической засечкой. Ее решение значительно проще для идеальной пары снимков. Случай съемки называется идеальным, если снимки получены с одной и той же высоты фотографирования, а их углы При указанных условиях справедливо: (69) Примем, что ось X совпадает с направлением базиса фотографирования, а ось Y параллельна плоскости снимков. Тогда BZ = BY = 0, BX = B.
ЗАВИСИМОСТЬ МЕЖДУ КООРДИНИТАМИ ТОЧКИ МЕСТНОСТИ И КООРДИНАТАМИ ЕЕ ИЗОБРАЖЕНИЯ НА ПАРЕ СНИМКОВ Задача определения пространственных координат точки местности по её изображению на снимках стереопары называется прямой пространственной фотограмметрической засечкой. Ее решение значительно проще для идеальной пары снимков. Случай съемки называется идеальным, если снимки получены с одной и той же высоты фотографирования, а их углы При указанных условиях справедливо: (69) Примем, что ось X совпадает с направлением базиса фотографирования, а ось Y параллельна плоскости снимков. Тогда BZ = BY = 0, BX = B.
 ЗАВИСИМОСТЬ МЕЖДУ КООРДИНИТАМИ ТОЧКИ МЕСТНОСТИ И КООРДИНАТАМИ ЕЕ ИЗОБРАЖЕНИЯ НА ПАРЕ СНИМКОВ Разность абсцисс p соответственных точек, измеренных на паре снимков, называется продольным параллаксом: p = x 1 – x 2, или на идеальной паре (71) Искомая формула зависимости координат точек местности и на паре снимков выглядит следующим образом: (73) (74)
ЗАВИСИМОСТЬ МЕЖДУ КООРДИНИТАМИ ТОЧКИ МЕСТНОСТИ И КООРДИНАТАМИ ЕЕ ИЗОБРАЖЕНИЯ НА ПАРЕ СНИМКОВ Разность абсцисс p соответственных точек, измеренных на паре снимков, называется продольным параллаксом: p = x 1 – x 2, или на идеальной паре (71) Искомая формула зависимости координат точек местности и на паре снимков выглядит следующим образом: (73) (74)
 ЗАВИСИМОСТЬ МЕЖДУ КООРДИНИТАМИ ТОЧКИ МЕСТНОСТИ И КООРДИНАТАМИ ЕЕ ИЗОБРАЖЕНИЯ НА ПАРЕ СНИМКОВ
ЗАВИСИМОСТЬ МЕЖДУ КООРДИНИТАМИ ТОЧКИ МЕСТНОСТИ И КООРДИНАТАМИ ЕЕ ИЗОБРАЖЕНИЯ НА ПАРЕ СНИМКОВ
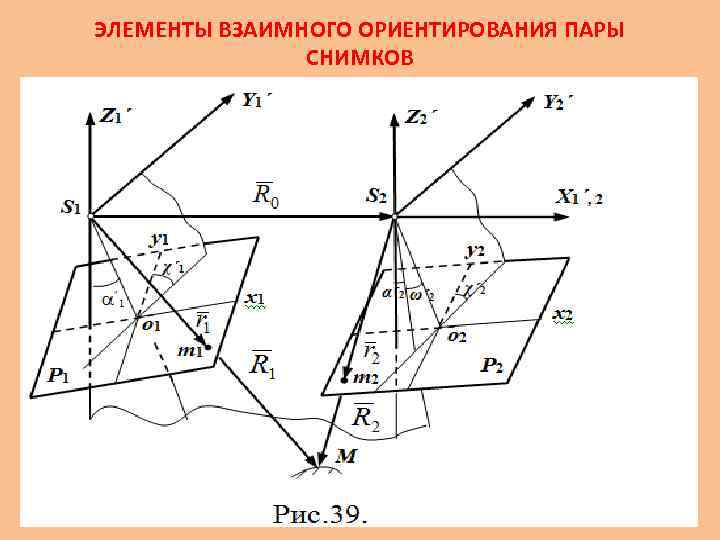
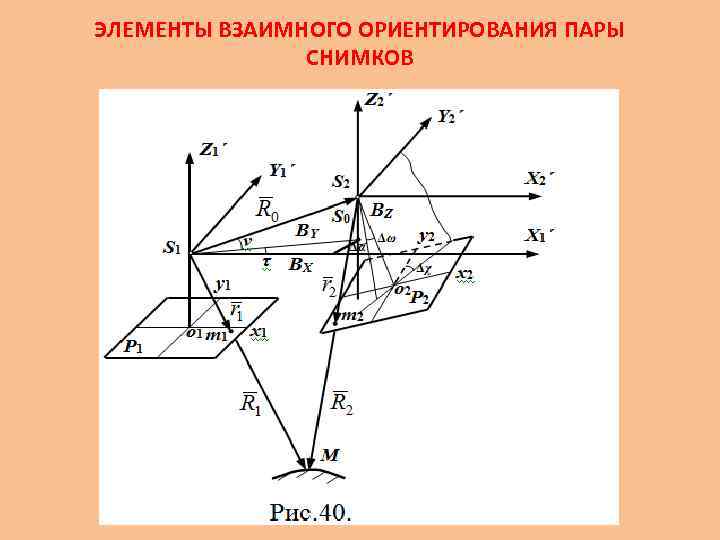
 ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ • Взаимное ориентирование снимков стереопары это установка их в положение, при котором любая пара соответственных лучей пересекается, то есть обеспечивается построение модели. Величины, определяющие такое положение снимков, называются элементами взаимного ориентирования (Эвз. О). • На практике выполнение условия пересечения соответственных лучей достигается поворотом обоих снимков или поворотами и смещениями только одного из них при неподвижном положении второго. В соответствии с этим различают две системы элементов взаимного ориентирования. В первой неподвижными считают базис фотографирования и главную базисную плоскость левого снимка; во второй – левый снимок.
ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ • Взаимное ориентирование снимков стереопары это установка их в положение, при котором любая пара соответственных лучей пересекается, то есть обеспечивается построение модели. Величины, определяющие такое положение снимков, называются элементами взаимного ориентирования (Эвз. О). • На практике выполнение условия пересечения соответственных лучей достигается поворотом обоих снимков или поворотами и смещениями только одного из них при неподвижном положении второго. В соответствии с этим различают две системы элементов взаимного ориентирования. В первой неподвижными считают базис фотографирования и главную базисную плоскость левого снимка; во второй – левый снимок.
 ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ
ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ
 ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ
ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ
 ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ
ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ
 ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ
ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ
 ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ
ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ
 ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ
ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ ПАРЫ СНИМКОВ
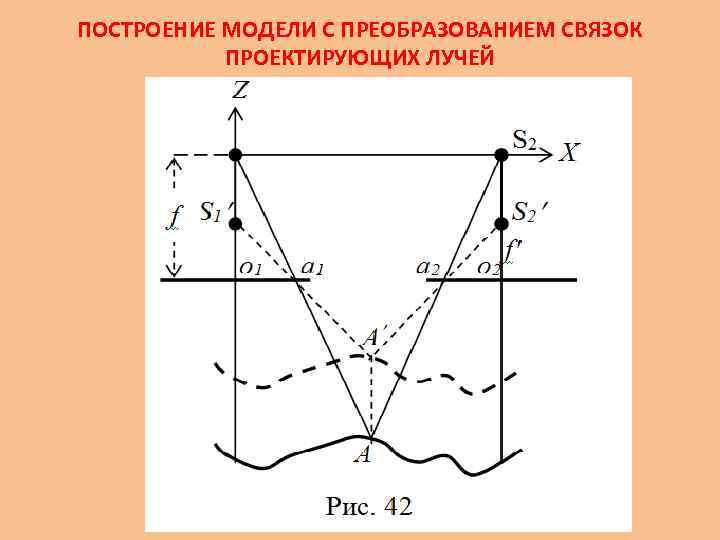
 ПОСТРОЕНИЕ МОДЕЛИ С ПРЕОБРАЗОВАНИЕМ СВЯЗОК ПРОЕКТИРУЮЩИХ ЛУЧЕЙ Иногда строят модель, когда расстояние f' от центра проекции до снимка не соответствует фокусному расстоянию f камеры АФА. В этом случае говорят, что связка проектирующих лучей преобразована. Для того чтобы понять к чему это приводит, изменим фокусное расстояние АФА в k раз при построении модели по паре горизонтальных снимков нормального случая съемки (Рис. 42).
ПОСТРОЕНИЕ МОДЕЛИ С ПРЕОБРАЗОВАНИЕМ СВЯЗОК ПРОЕКТИРУЮЩИХ ЛУЧЕЙ Иногда строят модель, когда расстояние f' от центра проекции до снимка не соответствует фокусному расстоянию f камеры АФА. В этом случае говорят, что связка проектирующих лучей преобразована. Для того чтобы понять к чему это приводит, изменим фокусное расстояние АФА в k раз при построении модели по паре горизонтальных снимков нормального случая съемки (Рис. 42).
 ПОСТРОЕНИЕ МОДЕЛИ С ПРЕОБРАЗОВАНИЕМ СВЯЗОК ПРОЕКТИРУЮЩИХ ЛУЧЕЙ
ПОСТРОЕНИЕ МОДЕЛИ С ПРЕОБРАЗОВАНИЕМ СВЯЗОК ПРОЕКТИРУЮЩИХ ЛУЧЕЙ
 ПОСТРОЕНИЕ МОДЕЛИ С ПРЕОБРАЗОВАНИЕМ СВЯЗОК ПРОЕКТИРУЮЩИХ ЛУЧЕЙ
ПОСТРОЕНИЕ МОДЕЛИ С ПРЕОБРАЗОВАНИЕМ СВЯЗОК ПРОЕКТИРУЮЩИХ ЛУЧЕЙ
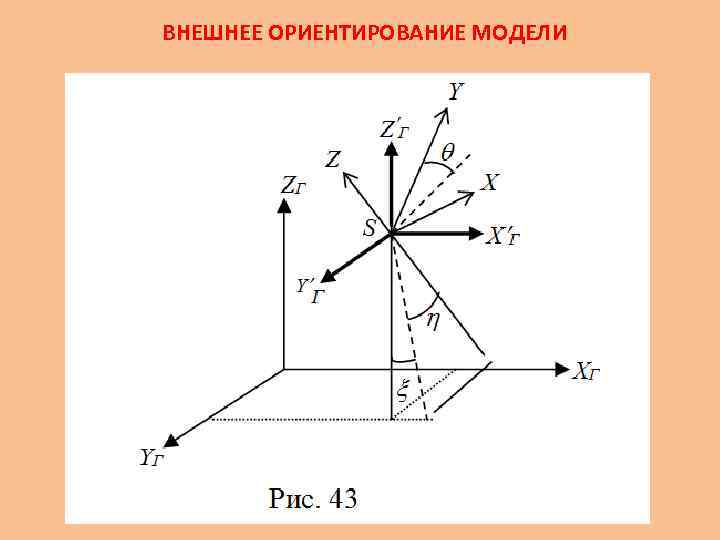
 ВНЕШНЕЕ ОРИЕНТИРОВАНИЕ МОДЕЛИ
ВНЕШНЕЕ ОРИЕНТИРОВАНИЕ МОДЕЛИ
 ВНЕШНЕЕ ОРИЕНТИРОВАНИЕ МОДЕЛИ
ВНЕШНЕЕ ОРИЕНТИРОВАНИЕ МОДЕЛИ
 ВНЕШНЕЕ ОРИЕНТИРОВАНИЕ МОДЕЛИ
ВНЕШНЕЕ ОРИЕНТИРОВАНИЕ МОДЕЛИ
 ВНЕШНЕЕ ОРИЕНТИРОВАНИЕ МОДЕЛИ
ВНЕШНЕЕ ОРИЕНТИРОВАНИЕ МОДЕЛИ


