Лекция 9 Тема Применение булевых функций

Лекция № 9 Тема: Применение булевых функций

Учебные вопросы: 1. Минимизация булевых функций в классе дизъюнктивных нормальных форм. 2. Применение булевых функций для анализа и синтеза дискретных устройств. Упрощение и преобразование комбинационных схем. 3. Применение булевых функций для анализа и синтеза релейно-контактных схем. Упрощение и преобразование релейно-контактных схем.

1. Минимизация булевых функций в классе дизъюнктивных нормальных форм Методы минимизации булевых функций: • Метод Квайна - Мак. Класски. • Метод Блейка - Порецкого. • Метод диаграмм Вейча. • Метод минимизирующих карт. • Метод Петрика. • Минимизация частично определенных булевых функций. • Минимизация систем булевых функций.

Любую логическую функцию f (x, y) можно представить в виде комбинаций конституэнт: C 0 = X Y ; C 1 = X Y ; C 2 = X Y ; C 3 = X Y ; Тогда СДНФ булевой функции f (x, y) запишется: СДНФ = (C 0 f(0, 0)) (C 1 f(0, 1)) (C 2 f(1, 0)) (C 3 f(1, 1, )) C 0 C 1 C 3

Алгоритм Квайна-Мак. Класски минимизации булевых функций 1. Все конституэнты единицы из СДНФ булевой функции f записываются их двоичными номерами. 2. Все номера разбиваются на непересекающиеся группы. Признак образования i-й группы: i единиц в каждом двоичном номере конституэнты единицы. 3. Склеивание производят только между номерами соседних групп. Склеиваемые номера отмечаются каким-либо знаком (зачеркиванием). 4. Производят всевозможные склеивания. Неотмеченные после склеивания номера являются простыми импликантами.

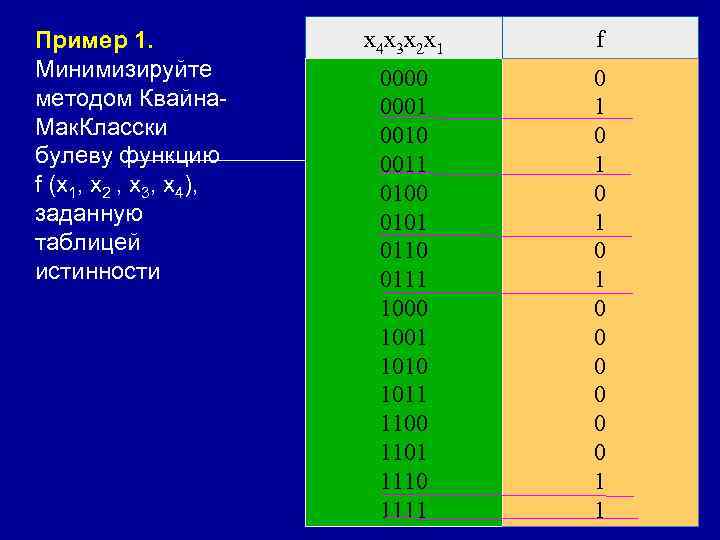
Пример 1. Минимизируйте методом Квайна- Мак. Класски булеву функцию f (x 1, x 2 , x 3, x 4), заданную таблицей истинности x 4 x 3 x 2 x 1 f 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 0 1 0 1 0 0 0 1 1

РЕШЕНИЕ: 1. Находим СДНФ функции. СДНФ = x 4 & x 3 & x 2 & x 1 x 4 & x 3 & x 2 & x 1 x 4 & x 3 & x 2 & x 1 x 4 & x 3 & x 2 & x 1 2. В СДНФ функции f заменим все конституэнты единицы их двоичными номерами: f = 0001 v 0011 v 0101 v 0111 v 1110 v 1111.

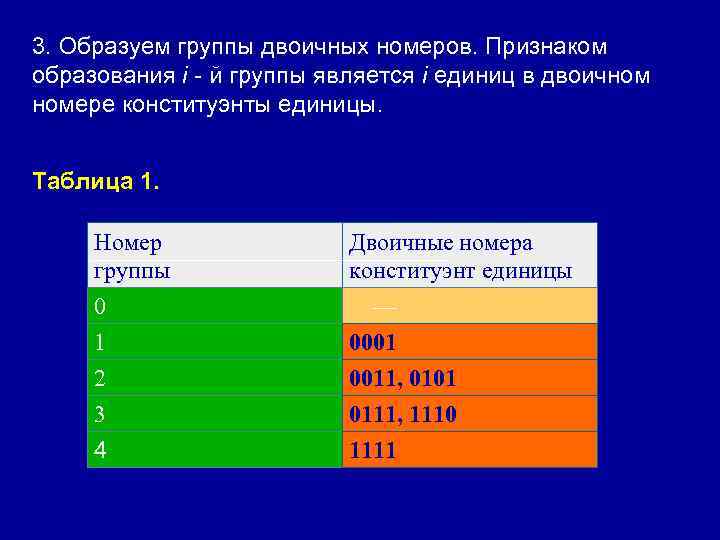
3. Образуем группы двоичных номеров. Признаком образования i - й группы является i единиц в двоичном номере конституэнты единицы. Таблица 1. Номер группы Двоичные номера конституэнт единицы 0 1 2 3 — 0001 0011, 0101 0111, 1110 1111 4

4. Склеим номера из соседних групп таблицы 1. Склеиваемые номера вычеркнем (Прим. - выделяем цветом). Результаты склеивания занесем в таблицу 2. Таблица 2. Номер группы Двоичные номера конституэнт единицы 1 00*1, 0*01 2 3 0*11, 01*1 *111, 111*

5. Склеим номера из соседних групп таблицы 2. Склеиваться могут только номера, имеющие звездочки в одинаковых позициях. Склеиваемые номера вычеркнем. Результаты склеивания занесем в таблицу 3. Таблица 3. Номер группы Двоичные номера конституэнт единицы 1 0**1 Получаем три простые импликанты: *111, 111*, 0**1.

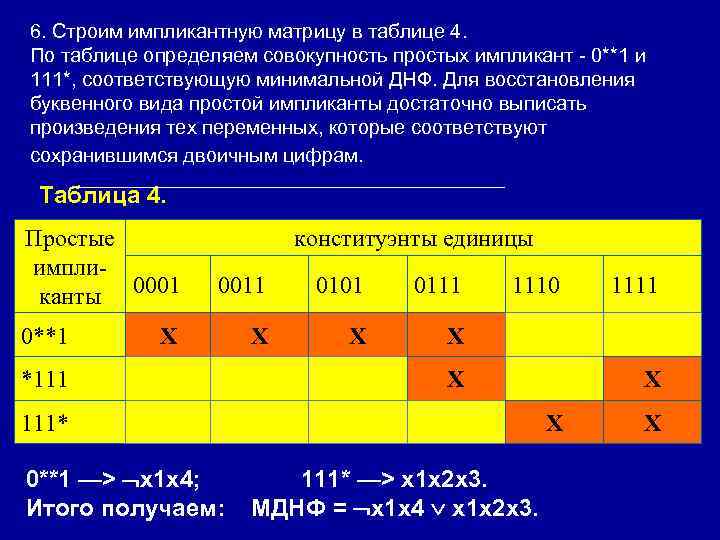
6. Строим импликантную матрицу в таблице 4. По таблице определяем совокупность простых импликант - 0**1 и 111*, соответствующую минимальной ДНФ. Для восстановления буквенного вида простой импликанты достаточно выписать произведения тех переменных, которые соответствуют сохранившимся двоичным цифрам. Таблица 4. Простые импликанты 0001 0**1 *111 X конституэнты единицы 0011 0101 0111 X X 1110 X X 111* 0**1 —> x 1 x 4; 111* —> x 1 x 2 x 3. Итого получаем: МДНФ = x 1 x 4 x 1 x 2 x 3. 1111 X Х Х

2. Применение булевых функций для анализа и синтеза дискретных устройств. Упрощение и преобразование комбинационных схем Логические устройства Комбинационные схемы Цифровые автоматы с памятью

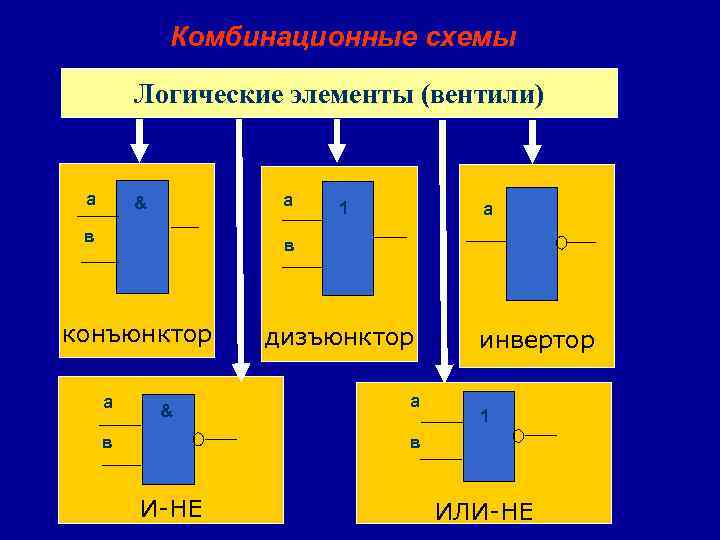
Комбинационные схемы Логические элементы (вентили) а а & в 1 а в конъюнктор а & дизъюнктор а инвертор 1 в в И-НЕ ИЛИ-НЕ

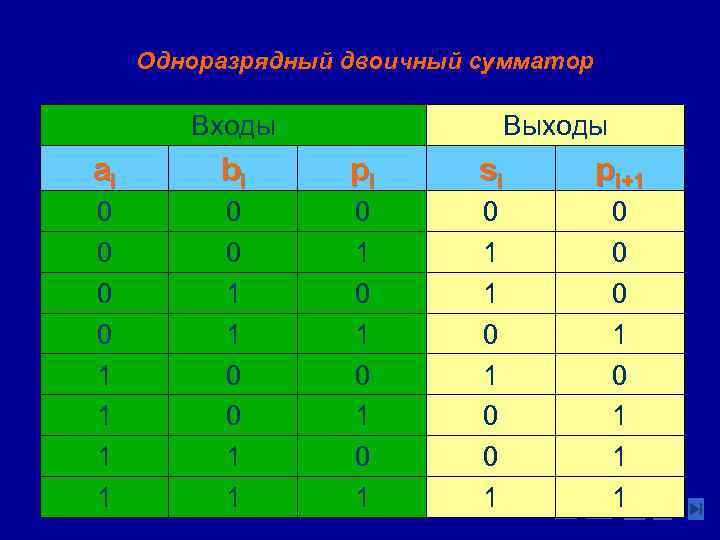
Одноразрядный двоичный сумматор Входы Выходы ai bi pi si pi+1 0 0 1 1 0 1 0 1 0 1 1 0 0 0 1 1 1

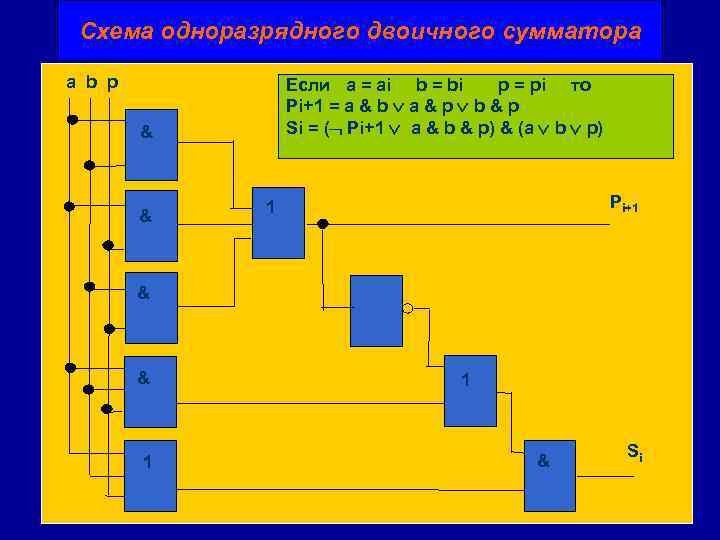
Схема одноразрядного двоичного сумматора a b p Если a = ai b = bi p = pi то Pi+1 = a & b a & p b & p Si = ( Pi+1 a & b & p) & (a b p) а & & Pi+1 1 & & 1 1 & Si

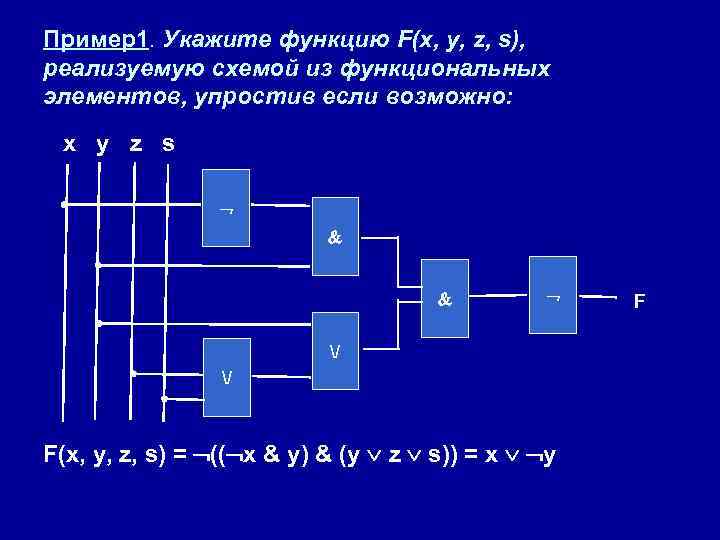
Пример1. Укажите функцию F(x, y, z, s), реализуемую схемой из функциональных элементов, упростив если возможно: x y z s / / F(x, y, z, s) = (( x & y) & (y z s)) = x y F

Пример2. Представьте функцию F(x, y, z) = z y x & z y в виде схемы из функциональных элементов, упростив если возможно. Преобразуем: F(x, y, z) = (z y) x & z y = x & z y x y z & / F

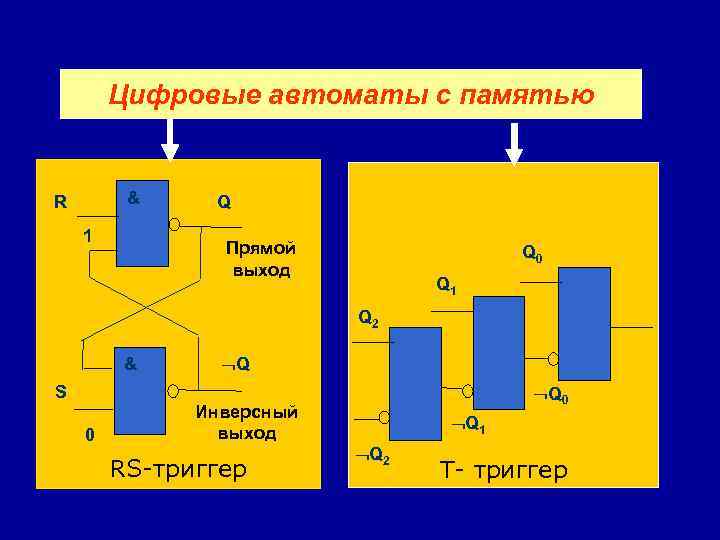
Цифровые автоматы с памятью & R 1 Q Прямой выход Q 0 Q 1 Q 2 & S 0 Q Инверсный выход RS-триггер Q 0 Q 1 Q 2 T- триггер

3. Применение булевых функций для анализа и синтеза релейно-контактных схем. Упрощение и преобразование релейно-контактных схем. Переключательной (релейно-контактной) схемой считают участок электрической цепи, включающий ряд переключателей. Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю поставим в соответствие логическую переменную х, которая принимает значение И в том случае, когда переключатель замкнут и схема проводит ток; если же переключатель разомкнут, то значение х будет Л. Будем считать, что переменные х и связаны таким образом, что когда контакт х замкнут, то разомкнут, и наоборот. Всей переключательной схеме можно поставить в соответствие логическую переменную, равную И, если схема проводит ток, и равную Л - если не проводит. Эта переменная является функцией от переменных, соответствующих всем переключателям схемы, и называется функцией проводимости.

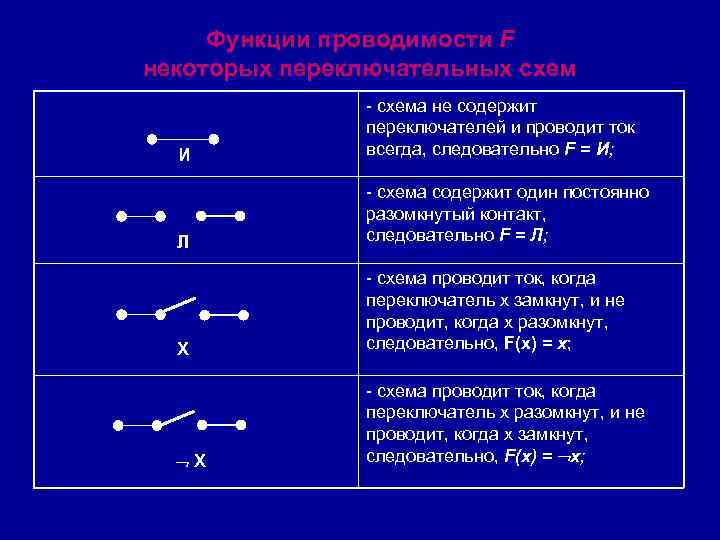
Функции проводимости F некоторых переключательных схем И - схема не содержит переключателей и проводит ток всегда, следовательно F = И; Л - схема содержит один постоянно разомкнутый контакт, следовательно F = Л; X - схема проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут, следовательно, F(x) = x; X - схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х замкнут, следовательно, F(x) = x;

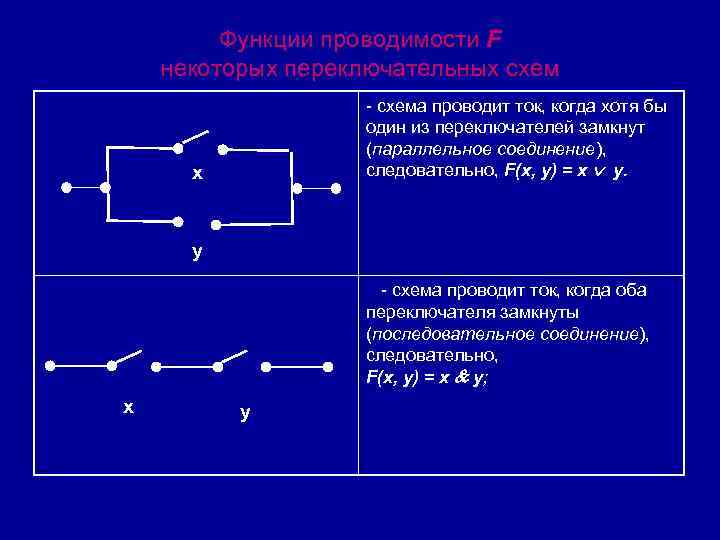
Функции проводимости F некоторых переключательных схем - схема проводит ток, когда хотя бы один из переключателей замкнут (параллельное соединение), следовательно, F(x, y) = x y. x y - схема проводит ток, когда оба переключателя замкнуты (последовательное соединение), следовательно, F(x, y) = x y; x y

Синтез схемы по заданным условиям ее работы сводится к : составлению функции проводимости по таблице истинности, отражающей эти условия; упрощению этой функции и построению соответствующей схемы. Анализ схемы сводится к: определению значений её функции проводимости при всех возможных наборах входящих в эту функцию переменных и получению упрощённой формулы. Пример1. Необходимо спроектировать (синтезировать) электрическую цепь, содержащую 4 переключателя x, y, z и t, такую, чтобы она проводила ток тогда и только тогда, когда замкнут контакт переключателя t и какой-нибудь из остальных трёх контактов. Функция имеет вид: F(x, y, z, t) = t (x y z). Схема имеет вид: x t y z

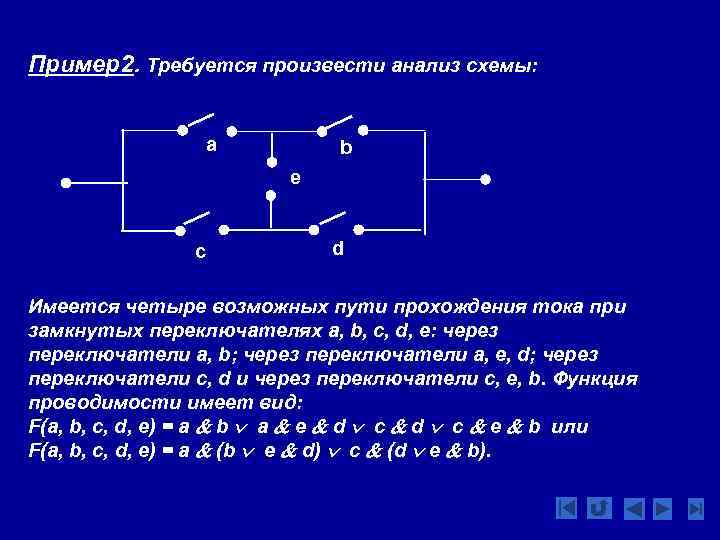
Пример2. Требуется произвести анализ схемы: a b e c d Имеется четыре возможных пути прохождения тока при замкнутых переключателях a, b, c, d, e: через переключатели a, b; через переключатели a, e, d; через переключатели c, d и через переключатели c, e, b. Функция проводимости имеет вид: F(a, b, c, d, e) = a b a e d c e b или F(a, b, c, d, e) = a (b e d) c (d e b).

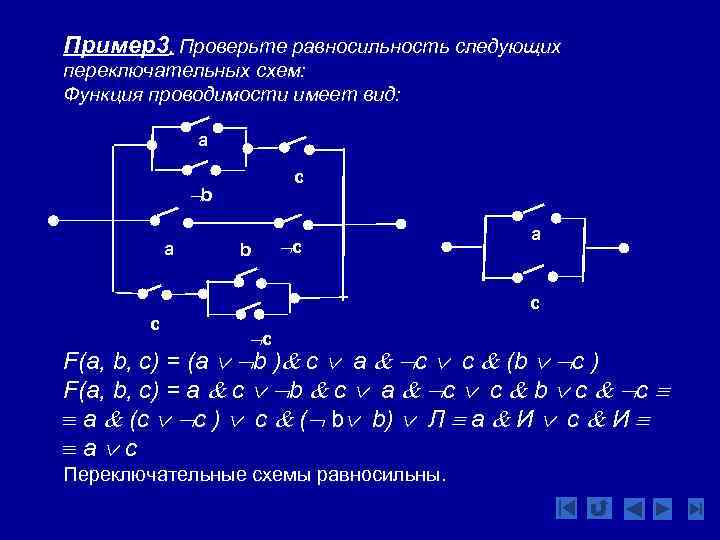
Пример3. Проверьте равносильность следующих переключательных схем: Функция проводимости имеет вид: a c b a b c a c c c F(a, b, c) = (a b ) c a c c (b c ) F(a, b, c) = a c b c a c c b c c º a (c c ) с ( b b) Л a И с И ºa с Переключательные схемы равносильны.

Литература: 1. Колесников Н. Г. Математические и логические основы информатики. Краснодар издат. Куб. АГУ. 2000 г. 224 с. 2. Калбертсон Дж. Т. Математика и логика цифровых устройств. -М. : Прсвещение, 1965. -267 с. 3. Кук Д. , Бейз Г. Компьютерная математика. – М. : Наука, 1990. 4. Мальцев А. И. Алгебраические системы. – М. : Наука, 1970. 5. Ершов Ю. Л. , Палютин Е. А. Математическая логика. – М. : Наука, 1979. 6. Верещагин Н. К. , Шень А. Начала теории множеств М. МЦНМО, 1999 г. , 127 с.