Лекция 9 Модели ЗО в телах.ppt
- Количество слайдов: 18

Лекция № 9 Тема лекции: Модели зародышеобразования в твердых телах ЗО в твердых телах с идеальной кристаллической решеткой Возникновение зародыша новой фазы с удельным объемом и структурой, отличными от материнской, приводят к появлению напряжений из-за деформации решетки в результате образования зародыша Упругая энергия матрицы и зародыша если • U 0 ik – деформация решетки, вызванная образованием зародыша материнской фазы и характеризующая при i≠k величину сдвига; • U 0 ii = U 0 xx + U 0 yy + U 0 zz – соответствующее относительное изменение объема • λ – модуль сдвига (отношение угла сдвига к касательному напряжению) λ –одинаков для новой и то материнской фаз возникающую упругую энергию матрицы и зародыша в общем виде можно 1 представить как (ΔGj )упр = λ (U 0 ik)2 jΩ

Упругая энергия ЗО Как и поверхностная энергия (ΔGj)пов = γ (jΩ )2/3, упругая энергия (ΔGj)упр пропорциональна объему зародыша, ее увеличение также приводит к возрастанию энергии Гиббса системы то Если Полное изменение энергии Гиббса системы при твердофазном образовании зародыша (1) зарождение новой фазы происходит лишь при условии Δμ ≥ λ(U 0 ik)2Ω используем типичные значения λ ≈ 105 Дж/ см 3, Ω ≈ 2. 10 -23 см 3, U 0 ik ≈ 3. 10 -2 Δμ ≥ 2. 10 -21 Дж Если Δμ ≈ ΔНΔТ/Т 0, где ΔН – теплота перехода (как правило, ≤ 7. 10 -21 Дж); То – температура перехода; ΔТ=Т 0 -Т – переохлаждение то Новая фаза может формироваться в объеме твердой материнской, если относительное переохлаждение 2 ΔТ/Т 0 ≥ 0. 3

Твердые тела с идеальной кристаллической решеткой критический зародыш возникает, когда следовательно При γ ≈ 5. 10 -6 Дж/см 2, λ ≈ 105 Дж/см 3, U 0 ik ≈ 3. 10 -2, Ω ≈ 2. 10 -23 см 3 и Δμ ≥ 2. 10 -21 Дж получаем jкр ≈140 Соответственно 3

В реальных кристаллических телах всегда присутствуют дефекты решетки, такие как • дефекты упаковки, дислокации и дислокационные системы, • структурные комплексы, создаваемые примесями и междоузельными атомами, • границы зерен и доменов и т. п. , которые повышают термодинамический потенциал кристалла Поэтому образование определенным образом расположенных относительно них областей новой фазы может быть сопряжено с выигрышем энергии по сравнению с образованием подобных областей в идеальной решетке Наличие дефектов приводит к уменьшению энергии ЗО, катализирует процесс ЗО в некоторых случаях настолько, что ЗНФ может протекать без преодоления значительных энергетических барьеров, с Еа порядка Еа диффузии 4

процессы ЗО на дефектах применительно к превращениям первого рода 1 Можно выделить два вида превращений первого рода, различающихся способами протекания • связан с перераспределением компонентов, не сопровождающимся изменением симметрии решетки, и назван когерентным, так как вдоль поверхности сопряжения фаз не происходит изменения расположения атомов в отсутствие релаксации упругих напряжений на начальных стадиях превращения 2 В превращениях второго вида – меняется симметрия решетки; такие превращения названы структурными Качественная общая картина зарождения когерентной фазы Образование зародыша – участка когерентной фазы в некоторой ограниченной области кристалла υ приводит к изменению энергии Гиббса кристалла 5

Энергия зарождения когерентной фазы при существовании достаточно резкой границы раздела фаз можно представить изменение ∆G в виде (2) Первое слагаемое в этом соотношении отражает изменения, связанные с возникновением поверхности раздела фаз, и пропорционально площади поверхности раздела S где γ – удельная поверхностная энергия С увеличением характерного размера зародыша R эта энергия возрастает как ~ R 2 Второй член, пропорциональный объему V, учитывает вклад как • изменения химического потенциала фаз Δμ при превращении, так и • работы на создание напряжений в ходе превращения: где λ – модуль сдвига; Um – наибольший компонент тензора деформации превращения Uik; ζ – числовой множитель, зависящий от формы области деформации 6 С увеличением R энергия ΔGV повышается как R 3

Энергия зарождения когерентной фазы Третье слагаемое отражает вклад взаимодействия зародыша с полем упругих напряжений σik(д) дефекта кристаллической решетки с ростом R убывает ~ R 3 -α – закон убывания напряжения дефекта Вследствие разного хода зависимости членов в выражении (2) от характерного размера зародыша и различным их вкладом в изменение энергии, с ростом R потенциал ΔGj сначала увеличивается, но после достижения некоторого критического значения Rкр, соответствующего критическому зародышу, убывает Форму критического зародыша находят из условия превращения в нуль первой производной ΔGj средняя кривизна в некоторой точке поверхности критического зародыша определяется разностью химических потенциалов фаз Δμ, поверхностной энергией зародыша γ, полной деформацией зародыша U*ik, и полным напряжением в этой точке где σ(з)ik – напряжение, создаваемое зародышем 7

гомогенное и гетерогенное фазообразование Зарождение новой фазы на линейных дефектах (дислокациях) Напряжения дислокации убывают с расстоянием r от ее оси σ(а)ik ~ Аik/r параметр Аik зависит от ориентации дислокации и вида зародыша и в целом характеризует убыль поверхностного натяжения зародыша в поле дислокации Вследствие того, что в этом случае показатель убывания напряжения α=1, (ΔGj)I подобно (ΔGj)S возрастает с увеличением характерного размера зародыша R пропорционально R 2 оставаясь отрицательным, но по размерности совпадая с (ΔGj)S По мере приближения к дислокации кривизна поверхности критического зародыша стремится к бесконечности критический зародыш представляет собой наблюдаемую экспериментально веретенообразную, вытянутую вдоль дислокации фигуру 8

Аik - убыль поверхностного натяжения зародыша в поле дислокации σ(а)ik ~ Аik/r Изменение параметра Aik приводит к тому, что при его приближении к γ энергия образования критического зародыша (ΔGj)кр ~ (γ-А)3/2 стремится к нулю, причем зародыш все более прижимается к дислокации. При А ≥ γ на дислокации возможно безбарьерное зарождение новой фазы При структурных превращениях, как и при когерентных, происходит однородная перестройка решетки 2 Но, если То в случае когерентных превращений степень искривления кристаллической решетки мала, и возможно когерентное сопряжение старой и новой фаз Структурные превращения, протекающие с изменением симметрии решетки, могут сопровождаться значительными ее искривлениями, требующими больших энергетических затрат И все же Дефекты кристалла, создающие большие локальные искажения решетки, способны перестроить часть материала около себя 9 до состояния, близкого к решетке новой фазы

Итак, для образования в однокомпонентной гомогенной системе зародышей НФ, способных к дальнейшему росту, необходимо значительное смещение фазы в метастабильную область, приводящее к достаточному для достижения критического состояния пересыщению (переохлаждению) Рассмотренные модели гомогенного зародышеобразования позволяют оценить уровень критического пересыщения, размер и количественный состав критического зародыша 10
Гетерогенное зародышеобразование Вероятность гетерогенного образования зародышей новой фазы увеличивается в следующих случаях • Появление пространственных макронеоднородностей с поверхностью раздела посторонние частицы, специально вводимые затравки, уже образовавшиеся кристаллические частицы • введение или присутствие в системе посторонних поверхностей стенки реакционного сосуда, подложки (оксиды металлов, полимеры) 11

Гетерогенное зародышеобразование В реальных твердых кристаллических телах ЗО может происходить не только гомогенно, но и в силу их кристаллического несовершенства и гетерогенно как в области nмакродефектов (трещин, сколов и т. п. ), так и nмикродефектов, в частности вблизи ступеней роста, дислокаций, границ зерен Хорошо известный пример выделение в объеме фотолизируемых кристаллов Ag. Br частичек металлического Ag в виде наноразмерных агломератов, объединенных в цепочки связано с преимущественной кристаллизацией серебра вдоль линий расположения дислокаций и на границах зерен 12

Гетерогенное зародышеобразование любые поверхности, на которых происходит образование зародышей, имеющие радиус кривизны более 10 -5 см, по отношению к формирующемуся зародышу можно рассматривать как плоские объем шарового сегмента (соотношение между высотой hj и диаметром основания 2 rj) выражается формулой h = R(1 -cosΘ) рассматриваем образование из 2 -фазной системы 3 -фазной с 3 повер-ми раздела: : матрица (м) – среда (с) с поверхностной энергией γмс, зародыш (з) – среда с поверхностной энергией γзс, и матрица – зародыш с γмз Схема модели изотропного ОЗ на Для линейной границы смачивания твердой поверхности: Θ - равновесный угол контакта; R (1) радиус кривизны сферической чем больше отношение γмс-γмз/ γзс, тем поверхности зародыша; h лучше смачивание высота сферического сегмента; r - радиус основания сегмента 13
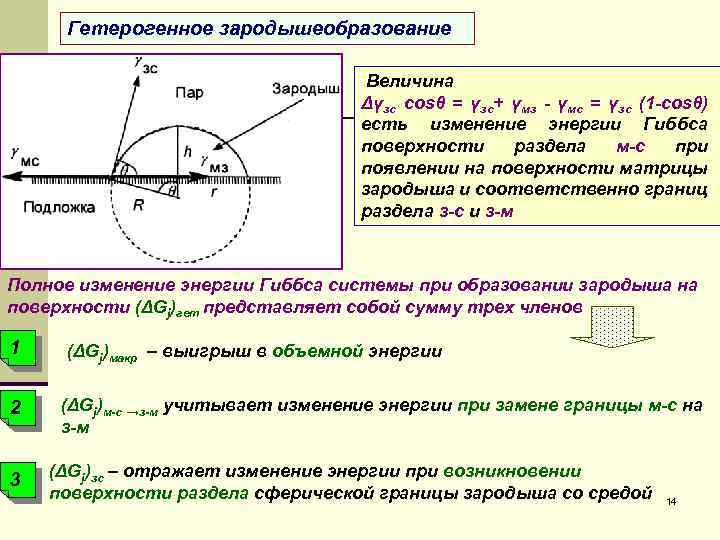
Гетерогенное зародышеобразование Величина Δγзс cosθ = γзс+ γмз - γмс = γзс (1 -cosθ) есть изменение энергии Гиббса поверхности раздела м-с при появлении на поверхности матрицы зародыша и соответственно границ раздела з-с и з-м Полное изменение энергии Гиббса системы при образовании зародыша на поверхности (ΔGj)гет представляет собой сумму трех членов 1 2 3 (ΔGj)макр – выигрыш в объемной энергии (ΔGj)м-с →з-м учитывает изменение энергии при замене границы м-с на з-м (ΔGj)зс – отражает изменение энергии при возникновении поверхности раздела сферической границы зародыша со средой 14

Гетерогенное зародышеобразование Полное изменение энергии Гиббса системы С учетом условия равновесного смачивания (1) (2), где Сопоставление уравнения (2) с выражением для ГЗ показывает, что для модели гетерогенно-конденсирующейся капли полное изменение энергии Гиббса системы равно полному изменению энергии системы при гомогенной конденсации, умноженной на функцию угла смачивания f(θ): 15

Критический зародыш Полное изменение энергии Гиббса системы достигает своего максимального значения при образовании критического зародыша: при (3) Сравнение (3) и показывает, что при данном Δμ (данном пересыщении) кривизна поверхности зародыша, образовавшегося как гомогенно в объеме МФ, так и гетерогенно на поверхности матрицы, одинакова Функция угла смачивания f(θ) изменяется от нуля (θ = 0 о- поверхность абсолютно смачиваемая) до 1 (θ = 180 о – поверхность абсолютно несмачиваемая) энергетический барьер гетерогенного образования критического зародыша на поверхности меньше соответствующего барьера гомогенного зарождения в объеме: Если вероятность ЗО на поверхности становится столь большой, что пересыщение 16 (переохлаждение) становится ниже величины, необходимой для гомогенного объемного ЗО

в случае абсолютно смачиваемой поверхности невозможно получить пар в присутствии твердой фазы, а следовательно ЗО будет протекать исключительно на поверхности твердой фазы Важно для металлизации поверхности функционализированных полимеров Т. о. , зарождение НФ на пространственных неоднородностях, в частности поверхности, намного выгоднее гомогенного ЗО в объеме Даже при умеренном смачивании (θ = 45 о) ((ΔGj)кр. гет ≈ 0. 2(ΔGj)кр. гом 17
18
Лекция 9 Модели ЗО в телах.ppt