лекция 9 СПИСКИ ОКОНЧАНИЕ ГРАФЫ План лекции

лекция 9 СПИСКИ (ОКОНЧАНИЕ). ГРАФЫ

План лекции Очередь Реализация с помощью списка Реализация с помощью циклического буфера Графы Определения Вычисление кратчайших расстояний с помощью очереди

Очередью называется линейный список, в котором все включения производятся на одном конце списка, все исключения – на другом его конце FIFO (first-in-first-out) – первый вошел, первый вышел Исключить Начало Включить Второй Третий Четвертый Конец

Операции работы с очередью create(&Q) – создает очередь makeempty (&Q) – делает очередь Q пустой front (&Q) – выдает значение первого элемента очереди, не удаляя его get(&Q) – выдает значение первого элемента очереди и удаляет его из очереди put(&Q, x) – помещает в конец очереди Q новый элемент со значением x empty (&Q) -- если очередь пуста, то 1 (истина), иначе 0 (ложь) destroy(&Q) -- уничтожает очередь

Реализация очереди с помощью списка struct Element { T struct Element * }; value; next; struct Queue { struct Element * }; front; back; typedef struct Queue typedef Element * Queue; ptr. Element;

Create, put void create(Queue *q) { q->front = q->back = NULL; } void put(Queue *q, T a) { ptr. Element p = malloc(sizeof(*p)); p->value = a; p->next = NULL; if (q->front == NULL) q->front = p; else q->back->next = p; q->back = p; }

Get, empty T get(Queue *q) { ptr. Element p = q->front; T a = p->value; q->front = p->next; free(p); if (q->front == NULL) q->back = NULL; return a; } int empty(const Queue *q) { return q->front == NULL; }

Реализация очереди с помощью циклического буфера value[ 6 0] [5] va lue va [3] Queue; ptr. Element; lue [4] e valu front 1] [ alue v ] va typedef struct Queue typedef T * val ue[ 7] ue[ val struct Queue { T *value; int front; int back; int size; }; back [2]

Create, put void create(Queue *q, int size) { q->value = malloc(*q->value*size); q->front = q->back = 0; q->size = size; } void put(Queue *q, T a) { q->value[q->back] = a; // Как узнать, что в очереди нет места? q->back = (q->back+1) % q->size; }

Get, empty T get(Queue *q) { T a = q->value[q->front]; q->front = (q->front+1) % q->size; return a; } int empty(const Queue *q) { return q->front == q->back; }

Пример работы с очередью int main() { Queue Q; create(&Q); // create(&Q, 100); put(&Q, 5); put(&Q, 7); while (!empty(Q)) { int b = get(Q); printf("%dn", b); } destroy(&Q); return 0; }

Дек (double-ended queue) очередь с двумя концами Деком называется линейный список, в котором включения и исключения производятся на обоих концах списка Включить или исключить Левый конец Включить или исключить Второй слева Третий слева или справа Второй справа Правый конец

Графы Очередь Реализация с помощью списка Реализация с помощью циклического буфера Графы Определения Вычисление кратчайших расстояний с помощью очереди

Упорядоченная пара Пусть А и В – множества Упорядоченная пара (а, b), состоящая из а А и b B, это конечное множество {a, b}} Упорядоченные пары (а, b) и (с, d) равны, если а = с и b = d Почему? Чем отличается упорядоченная пара от множества {а, b}?

Декартово произведение Декартовым произведением Ах. В множеств A и B называется множество упорядоченных пар { (а, b) | а А и b B } Пример A = {1, 2} В = {2, 3, 4} Aх. B = {(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4)}

Отношения Пусть А и В —множества Отношением из А в В называется любое подмножество множества Ах. В A называется областью определения отношения R В называется множеством значений отношения R Факт (а, b) R сокращенно записывается а. Rb Отношение {(b, а) | (а, b) R} называется обратным к отношению R и часто обозначается через R-1. Ax. B B R A

Виды отношений Пусть A—множество Отношение R называется на А рефлексивным, если а. Rа для всех a из А симметричным, если а. Rb влечет b. Ra для a и b из A транзитивным, если для любых а, b и с из A из а. Rb и b. Rс следует а. Rс Рефлексивное, симметричное и транзитивное отношение называется отношением эквивалентности Отношение эквивалентности на множестве A разбивает множество A на непересекающиеся подмножества, называемые классами эквивалентности Приведите примеры каждого вида отношений

Графы Графом называется пара (А, R), где А — конечное множество, а R — отношение на множестве А Элементы А называются вершинами (узлами) Элементы R называются дугами (ребрами) Если отношение R несимметричное, то граф ориентированный Если отношение R симметричное, то граф неориентированный

Изображение графов на плоскости Вершины графа изображают точками Дуги графа изображают прямо- или криволинейных отрезков Пример изображения графа на плоскости A={1, 2, 3, 4} , R = {(1, 1), (1, 2), (2, 3), (2, 4), (3, 4), (4, 1), (4, 3)} 2 1 3 4

Изображение графов на плоскости Изображения дуг графа могут пересекаться -- точки пересечения не являются вершинами Граф, который можно изобразить на плоскости без пересечений дуг, называется планарным. Пример различных изображений графа на плоскости A={1, 2, 3, 4} , R = {(1, 2), (1, 3), (2, 4), (3, 4), (4, 1)} 2 1 3 4

Дуги графа Пара (а, b) R называется дугой (ребром) графа G Дуга выходит из вершины а и входит в вершину b Вершина а предшествует вершине b, а вершина b следует за вершиной a Вершина b смежна с вершиной a a b

Путь и цикл в графе Последовательность вершин (а 0, а 1, . . . , аn), n≥ 1, называется путем (маршрутом) длины n из вершины а 0 в вершину аn, если для каждого 1≤i≤n существует дуга, выходящая из вершины аi-1 и входящая в вершину аi Если существует путь из вершины а 0 в вершину аn, то говорят, что аn достижима из а 0 Циклом называется путь (а 0, а 1, . . . , аn), т. ч. а 0 = аn

Путь и цикл в графе A={1, 2, 3, 4} R = {(1, 1), (1, 2), (2, 3), (2, 4), (3, 4), (4, 1), (4, 3)} Путь ( 1, 2, 4, 3 ) Цикл ( 1, 2, 3, 4, 1 ) 2 1 3 4

Степень вершины Степенью по входу (полустепенью входа) вершины называется число входящих в нее дуг Степенью по выходу (полустепенью исхода) вершины называется число выходящих из нее дуг Если граф неориентированный, то степенью вершины называется количество инцидентных с ней ребер 2 1 3 4 Для вершины 2: полустепень входа = 1 полустепень исхода = 2

Ациклические графы Ациклическим графом называется (ориентированный) граф, не имеющий циклов Вершина, степень по входу которой равна 0, называется базовой Вершина, степень по выходу которой равна 0, называется листом (концевой вершиной) 5 8 3 2 1 6 9 4 7

Дуга и путь в ациклическом графе Пусть (a, b) – дуга в ациклическом графе Вершина a называется прямым предком b, b называется прямым потомком a Если существует путь из a в b, то a называется предком b, b называется потомком a a b

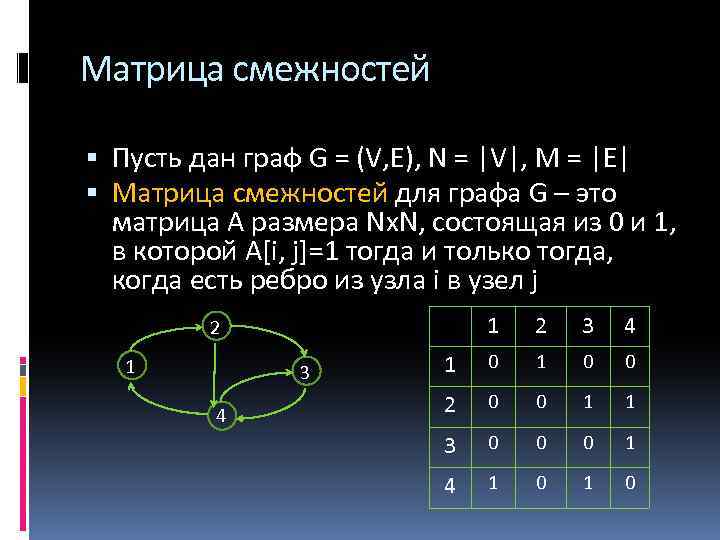Матрица смежностей Пусть дан граф G = (V, E), N = |V|, M = |E| Матрица смежностей для графа G – это матрица A размера Nх. N, состоящая из 0 и 1, в которой A[i, j]=1 тогда и только тогда, когда есть ребро из узла i в узел j 1 2 3 4 1 0 0 2 0 0 1 1 3 0 0 0 1 4 1 0 2 1 3 4

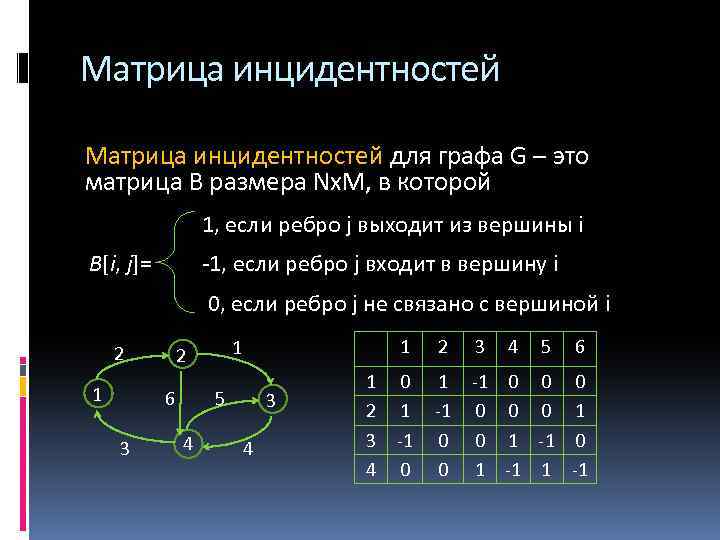Матрица инцидентностей для графа G – это матрица B размера Nх. M, в которой 1, если ребро j выходит из вершины i B[i, j]= -1, если ребро j входит в вершину i 0, если ребро j не связано с вершиной i 2 1 6 3 1 1 2 5 4 3 4 1 2 3 4 5 6 0 1 -1 0 0 0 1 0 1 -1

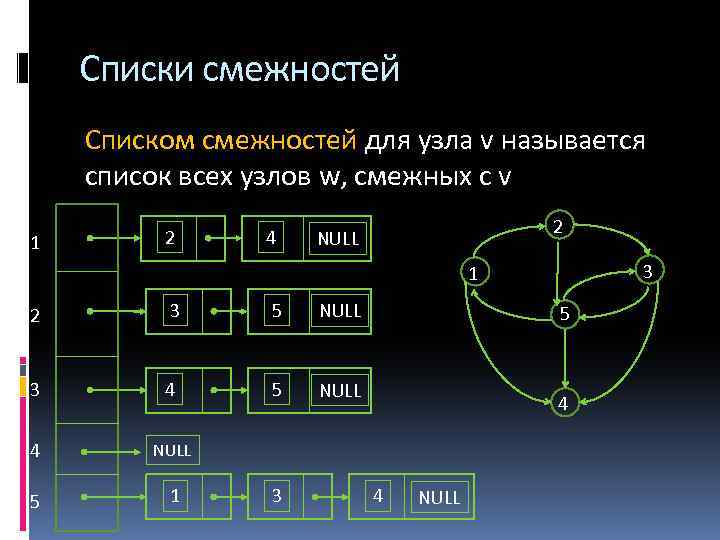Списки смежностей Списком смежностей для узла v называется список всех узлов w, смежных с v 1 2 4 2 NULL 3 1 2 3 5 NULL 3 4 5 NULL 4 NULL 5 1 3 5 4 4 NULL

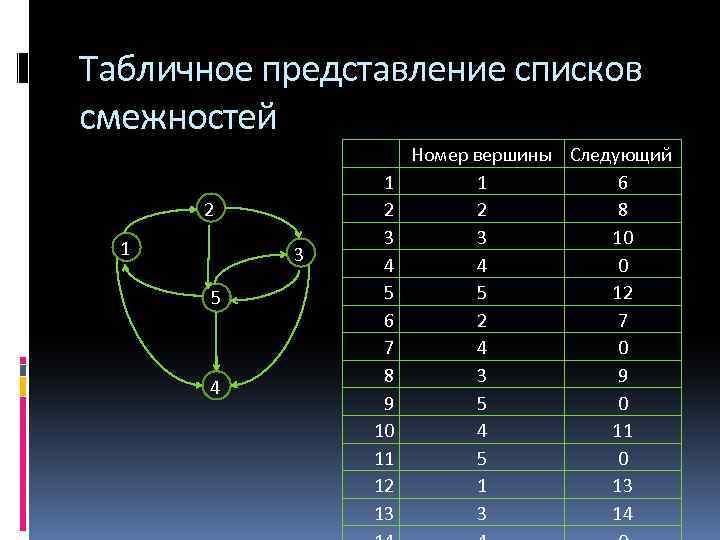Табличное представление списков смежностей 2 1 3 5 4 1 2 3 4 5 6 7 8 9 10 11 12 13 Номер вершины Следующий 1 6 2 8 3 10 4 0 5 12 2 7 4 0 3 9 5 0 4 11 5 0 1 13 3 14

Метод поиска в ширину Один из способов нумерации вершин произвольного графа Проектирование ИС и печатных плат, . . . Основа большого числа алгоритмов Поиск кратчайших путей Вычисление максимального потока в графе Проверка связности Breadth-first search, BFS

Метод поиска в ширину Пусть дан граф G и выбрана некоторая его вершина s Поиск в ширину вычисляет для каждой вершины u два номера П[u] предшественика вершины u при поиске в ширину d[u] кратчайшее расстояние от s до u Схема алгоритма Шаг 1: d[s] = 0 Шаг n: обрабатываем все вершины на расстоянии n-1 от s Каждого соседа v вершины u с пометкой d[u] = n-1 нумеруем П[v] = u и d[v] = n

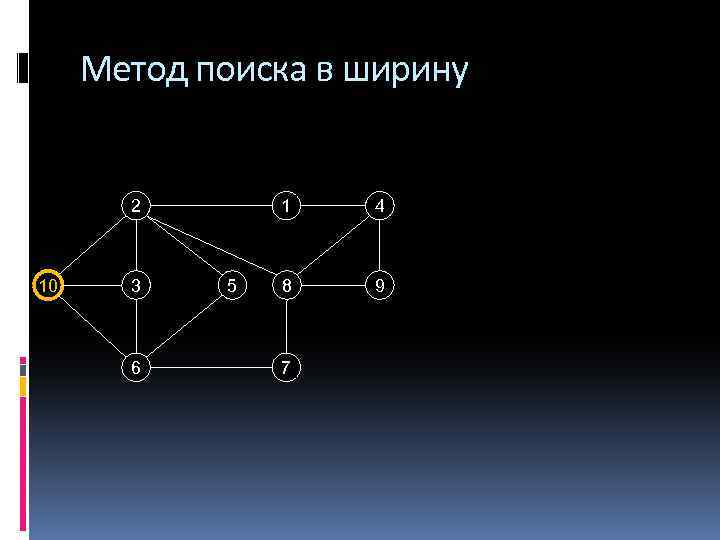Метод поиска в ширину 2 10 3 6 1 5 4 8 9 7

Метод поиска в ширину d[2] = 1 2 10 3 1 5 4 8 9 d[3] = 1 6 d[6] = 1 7

Метод поиска в ширину d[2] = 1 d[1] = 2 2 1 4 8 9 d[5] = 2 10 3 d[3] = 1 6 d[6] = 1 5 d[8] = 2 7 d[7] = 2

Метод поиска в ширину d[2] = 1 d[1] = 2 d[4] = 3 1 4 8 9 d[8] = 2 d[9] = 3 2 d[5] = 2 10 3 d[3] = 1 6 d[6] = 1 5 7 d[7] = 2

Метод поиска в ширину d[2] = 1 d[1] = 2 d[4] = 3 1 4 V Расстояние до 10 Путь через 1 2 2 2 1 3 1 4 3 2, 1 7 5 2 2 или 6 d[7] = 2 6 1 3 7 2 6 8 2 2 9 3 2, 8 2 d[5] = 2 10 3 d[3] = 1 6 d[6] = 1 5 8 9 d[8] = 2 d[9] = 3

Алгоритм BFS (матрица смежности граф G, число вершин n, вершина s) { for (u = 0; u < n; u++) d[u] = n; // почему? } d[s] = 0; put(s, Q); while (! empty(Q)) { u = get(Q); for (v = 0; v < n; v++) if (G[v][u] == 1) { // для всех соседей u if (d[v] > d[u]+1) { d[v]= d[u]+1; put(Q, v); }} }

Заключение Очередь Реализация с помощью списка Реализация с помощью циклического буфера Графы Определения Вычисление кратчайших расстояний с помощью очереди

КОНЕЦ ЛЕКЦИИ

Односвязный граф Граф называется сильно связным, если для любых двух разных вершин а и b существует путь из a в b. Содержит одну компоненту связности - Существует путь из любой вершины в любую другую вершину - Существует путь из заданной вершины в любую другую вершину - Содержит связный подграф, включающий все вершины исходного графа - Содержит в качестве подграфа дерево, включающее все вершины исходного графа (такое дерево называется остовным) - При произвольном делении его вершин на 2 группы всегда существует хотя бы 1 ребро, соединяющее пару вершин из разных групп. Компонента связности графа — некоторое множество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества.

Линейный список - это множество, состоящее из n (n≥ 0) узлов (элементов) X[1], X[2], … , X[n], структурные свойства которого ограничены линейным (одномерным) относительным положением узлов (элементов), т. е. следующими условиями: если n > 0, то X[1] – первый узел; если 1 < k < n, то k-му узлу X[k] предшествует узел X[k-1], а за узлом X[k] следует узел X[k+1]; X[n] – последний узел.

Реализация двусвязного списка struct Tlist 2 { char word[256]; //область данных struct Tlist 2 *next; //ссылка на следующий узел struct Tlist 2 *prev; //ссылка на предыдущий узел }; struct Tlist 2 * Head = NULL; //голова списка struct Tlist 2* new_el_2(char new. Word[]) { struct Tlist 2 * p=(struct Tlist 2 *) malloc( sizeof(struct Tlist 2)); if(p){ strcpy(p->word, new. Word); //записать слово p->next = NULL; //следующего узла нет p->prev = NULL; //предыдущего узла нет } return p; //результат функции – адрес элемента }

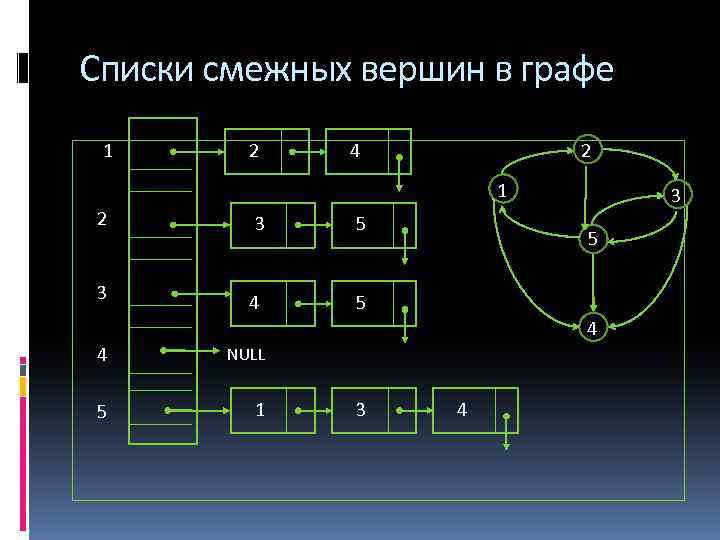Списки смежных вершин в графе 1 2 4 2 1 2 3 3 5 4 3 5 5 4 4 NULL 5 1 3 4

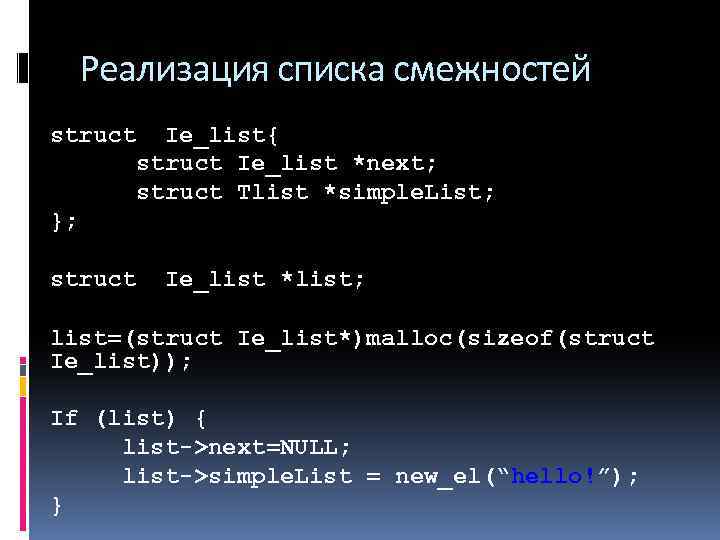Реализация списка смежностей struct Ie_list{ struct Ie_list *next; struct Tlist *simple. List; }; struct Ie_list *list; list=(struct Ie_list*)malloc(sizeof(struct Ie_list)); If (list) { list->next=NULL; list->simple. List = new_el(“hello!”); }

Реализация односвязного списка struct data_and_link { char data[256]; struct data_and_link *link; }; // данные // связь // список данных typedef struct data_and_link *list; list add_data(const char d[], list L) { list new_L = (list) malloc(sizeof(*new_L)); if (new_L != NULL) { // успешно? strcpy(new_L->data, d); // новые данные new_L->link = L; // привязаны старым } return new_L; // результат – обновлённый список }

Пример работы с односвязным списком struct Tlist *head=NULL; struct Tlist *p; int main() { list L = add_data("A", add_data("B", add_data("C", NULL))); } p = (struct Tlist*) malloc(sizeof(struct Tlist)); p->data = 5; p->next = NULL; head = p; head p 5 NULL

Вставка элемента в односвязный список после элемента с адресом prev typedef struct Tlist *Node; //указатель на элемент void Add. After (Node prev, char data[]) { Node cur = new_el(data); if (cur) { cur ->next = prev->next; prev->next = cur; } }

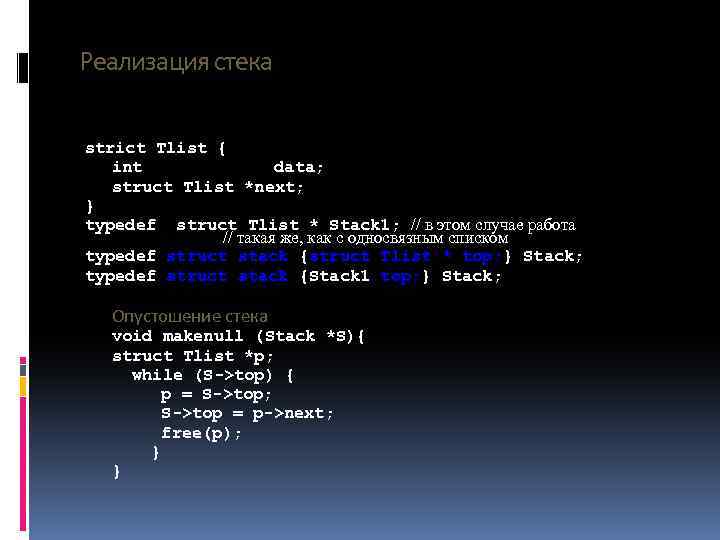Реализация стека strict Tlist { int data; struct Tlist *next; } typedef struct Tlist * Stack 1; // в этом случае работа // такая же, как с односвязным списком typedef struct stack {struct Tlist * top; } Stack; typedef struct stack {Stack 1 top; } Stack; Опустошение стека void makenull (Stack *S){ struct Tlist *p; while (S->top) { p = S->top; S->top = p->next; free(p); } }

Создание стека Stack * create () { Stack *S; S = (Stack *)malloc(sizeof(Stack)); S->top = NULL; return S; } Верхушка стека int top (Stack *S) { if (S->top) return (S->top->data); else return 0; //здесь может быть реакция на //ошибку – обращение к пустому стеку }

Взятие верхнего элемента стека int pop(Stack *S){ int a; struct Tlist *p; p = S->top; a = p->data; S-> top = p->next; free(p); return a; }

Помещение в стек нового элемента void push(int a, Stack *S){//return NULL? struct Tlist *p; p =(struct Tlist *)malloc(sizeof(struct Tlist)); if(p) { p->data = a; p->next = S-> top; S->top = p ; } } Проверка на пустоту int empty (Stack *S) { return (S->top == NULL); }