Лекция 9 Солодухин Е А Пересечение

Лекция № 9 Солодухин Е. А.

Пересечение прямой с поверхностью

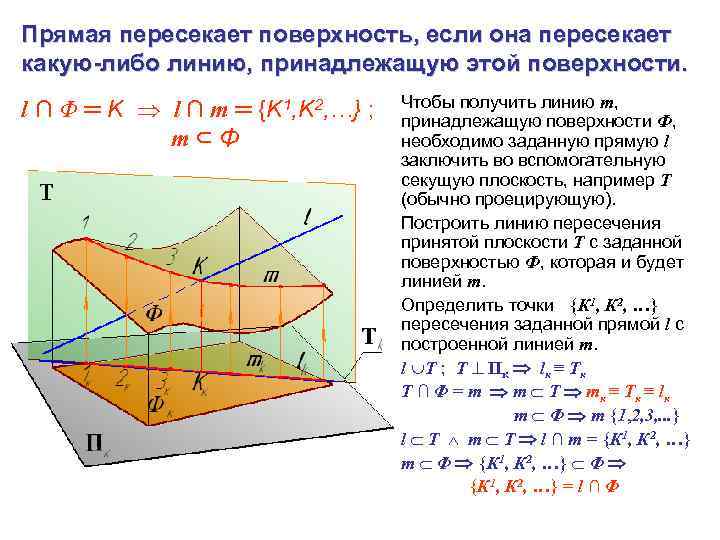Прямая пересекает поверхность, если она пересекает какую-либо линию, принадлежащую этой поверхности. l ∩ Φ ═ K l ∩ m ═ {K 1, K 2, …} ; m⊂Φ Чтобы получить линию m, принадлежащую поверхности Ф, необходимо заданную прямую l заключить во вспомогательную секущую плоскость, например Т (обычно проецирующую). Построить линию пересечения принятой плоскости Т с заданной поверхностью Ф, которая и будет линией m. Определить точки {К 1, К 2, …} пересечения заданной прямой l с построенной линией m. l Т ; Т Пк lк ≡ Тк Т ∩ Φ = m m Т mк ≡ Тк ≡ lк m Φ m {1, 2, 3, . . . } l Т m Т l ∩ m = {К 1, К 2, …} m Φ {К 1, К 2, …} = l ∩ Φ

Плоскость Т следует выбирать так, чтобы линия m на проекциях имела наиболее простую форму – прямой, ломаной или окружности. В противном случае необходимо построение дополнительной проекции.

Алгоритм решения задачи на построение точек пересечения прямой с поверхностью

Взаимное положение прямой линии и плоскости

Прямая по отношению к плоскости может занимать следующие положения: • Принадлежать; • Быть параллельной; • Пересекать; • Быть перпендикулярной.

Прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости. l ‖T l ‖ m ; m T Прямая пересекает плоскость, если она пересекает какую-либо прямую, принадлежащую этой плоскости. l ∩T l ∩ m ; m T Прямая принадлежит плоскости, если она тождественна какой-либо прямой, принадлежащей этой плоскости. l T l ≡ m ; m T

Плоскость Т задана треугольником АВС. Необходимо определить положение прямой l по отношению к этой плоскости. Выбрано l 2≡ m 2 l 1 ‖ m 1 l ‖ T Выбрано l 1≡ m 1 l 2 ∩ m 2= K 2 l ∩ T =K Выбрано l 1≡ m 1 l 2 ≡ m 2 l ⊂ T

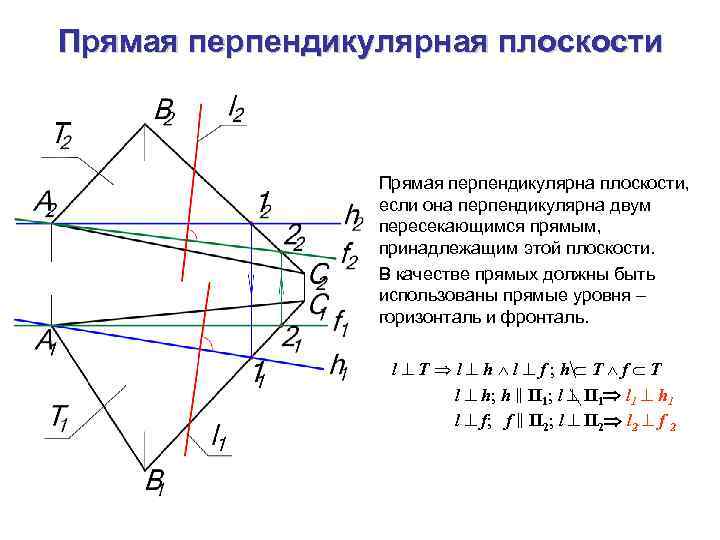Прямая перпендикулярная плоскости Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. В качестве прямых должны быть использованы прямые уровня – горизонталь и фронталь. l T l h l f; h T f T l h; h ‖ П 1; l П 1 l 1 h 1 l f; f ‖ П 2; l П 2 l 2 f 2

Пересечение прямой с гранной поверхностью

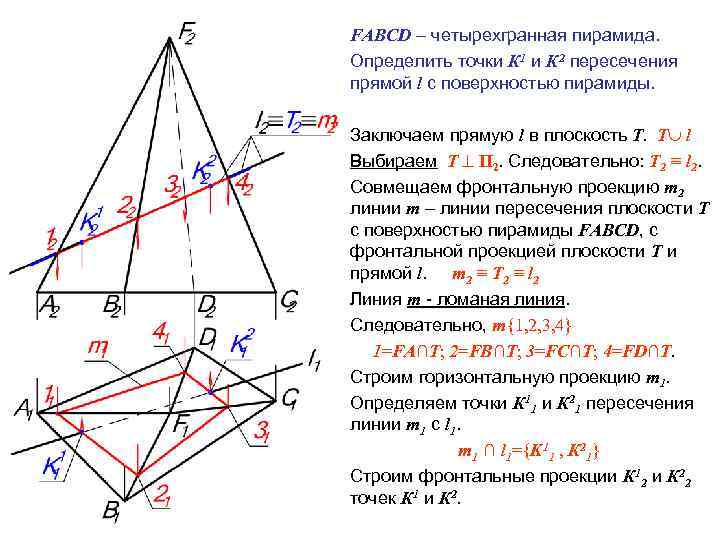FABCD – четырехгранная пирамида. Определить точки К 1 и К 2 пересечения прямой l с поверхностью пирамиды. Заключаем прямую l в плоскость Т. Т l Выбираем Т П 2. Следовательно: Т 2 ≡ l 2. Совмещаем фронтальную проекцию m 2 линии m – линии пересечения плоскости Т с поверхностью пирамиды FABCD, с фронтальной проекцией плоскости Т и прямой l. m 2 ≡ Т 2 ≡ l 2 Линия m - ломаная линия. Следовательно, m{1, 2, 3, 4} 1=FA∩T; 2=FB∩T; 3=FC∩T; 4=FD∩T. Строим горизонтальную проекцию m 1. Определяем точки К 11 и К 21 пересечения линии m 1 с l 1. m 1 ∩ l 1={K 11 , К 21} Строим фронтальные проекции К 12 и К 22 точек К 1 и К 2.

Пересечение прямой с конической поверхностью

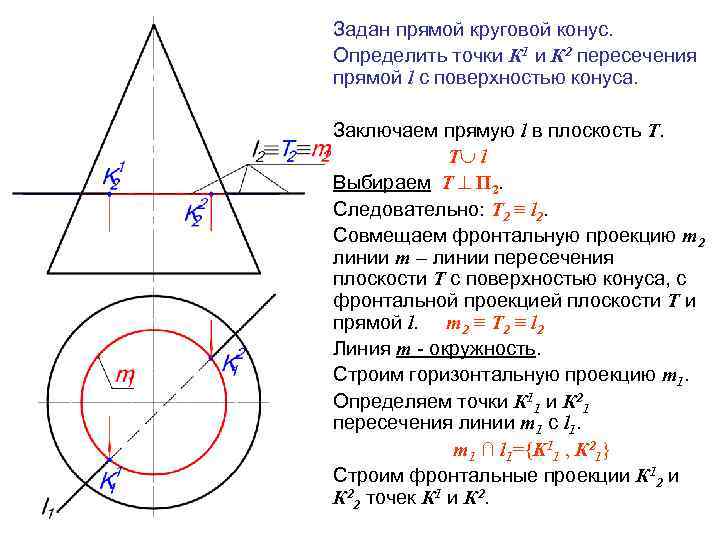Задан прямой круговой конус. Определить точки К 1 и К 2 пересечения прямой l с поверхностью конуса. Заключаем прямую l в плоскость Т. Т l Выбираем Т П 2. Следовательно: Т 2 ≡ l 2. Совмещаем фронтальную проекцию m 2 линии m – линии пересечения плоскости Т с поверхностью конуса, с фронтальной проекцией плоскости Т и прямой l. m 2 ≡ Т 2 ≡ l 2 Линия m - окружность. Строим горизонтальную проекцию m 1. Определяем точки К 11 и К 21 пересечения линии m 1 с l 1. m 1 ∩ l 1={K 11 , К 21} Строим фронтальные проекции К 12 и К 22 точек К 1 и К 2.

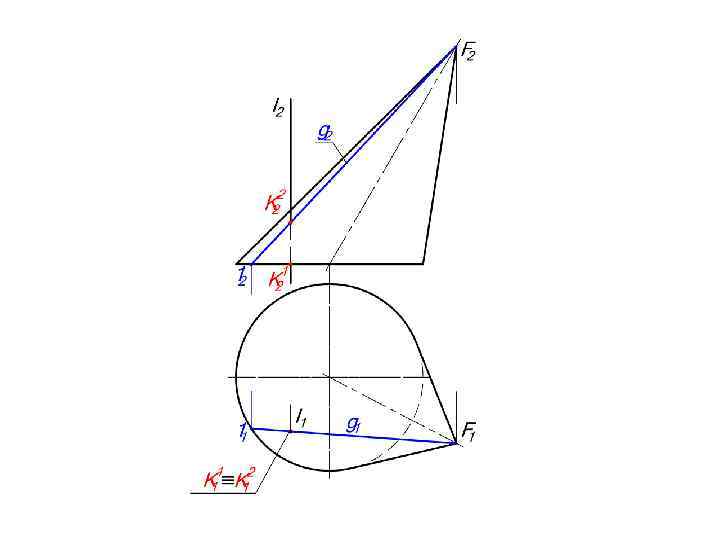
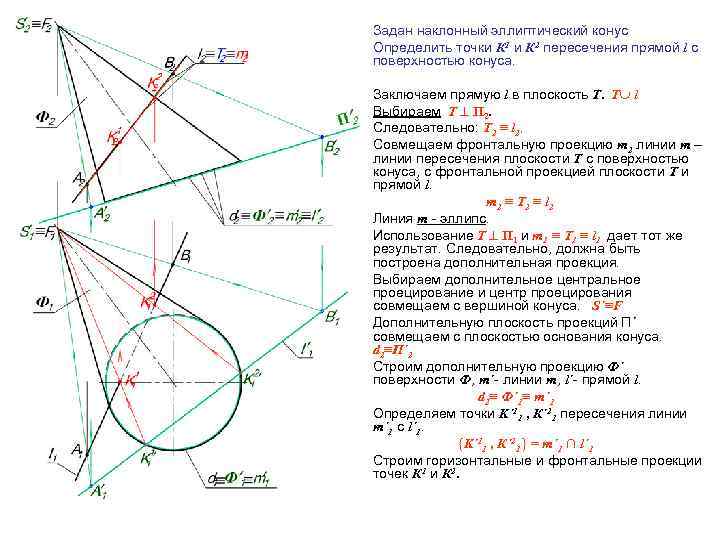Задан наклонный эллиптический конус Определить точки К 1 и К 2 пересечения прямой l с поверхностью конуса. Заключаем прямую l в плоскость Т. Т l Выбираем Т П 2. Следовательно: Т 2 ≡ l 2. Совмещаем фронтальную проекцию m 2 линии m – линии пересечения плоскости Т с поверхностью конуса, с фронтальной проекцией плоскости Т и прямой l. m 2 ≡ Т 2 ≡ l 2 Линия m - эллипс. Использование Т П 1 и m 1 ≡ Т 1 ≡ l 1 дает тот же результат. Следовательно, должна быть построена дополнительная проекция. Выбираем дополнительное центральное проецирование и центр проецирования совмещаем с вершиной конуса. S´≡F Дополнительную плоскость проекций П´ совмещаем с плоскостью основания конуса. d 2≡П´ 2 Строим дополнительную проекцию Ф´ поверхности Ф, m´- линии m, l´- прямой l. d 2≡ Ф´ 1≡ m´ 1 Определяем точки K´ 11 , К´ 21 пересечения линии m´ 1 с l´ 1. {K´ 11 , К´ 21} = m´ 1 ∩ l´ 1 Строим горизонтальные и фронтальные проекции точек К 1 и К 2.

Пересечение прямой с цилиндрической поверхностью

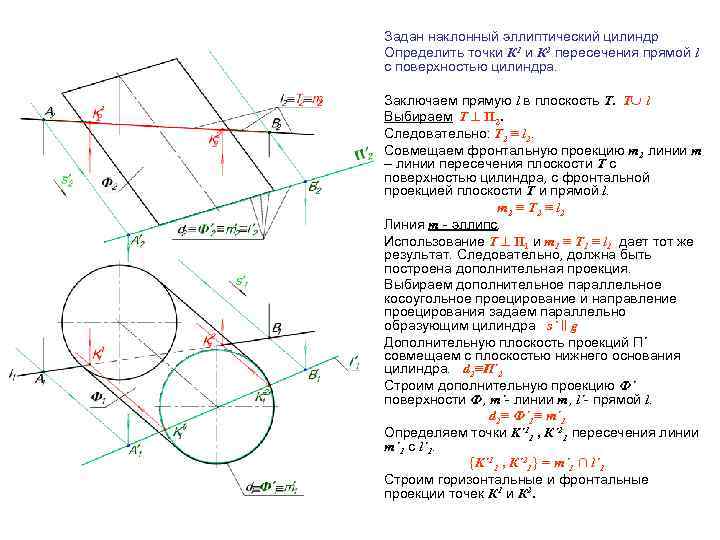Задан наклонный эллиптический цилиндр Определить точки К 1 и К 2 пересечения прямой l с поверхностью цилиндра. Заключаем прямую l в плоскость Т. Т l Выбираем Т П 2. Следовательно: Т 2 ≡ l 2. Совмещаем фронтальную проекцию m 2 линии m – линии пересечения плоскости Т с поверхностью цилиндра, с фронтальной проекцией плоскости Т и прямой l. m 2 ≡ Т 2 ≡ l 2 Линия m - эллипс. Использование Т П 1 и m 1 ≡ Т 1 ≡ l 1 дает тот же результат. Следовательно, должна быть построена дополнительная проекция. Выбираем дополнительное параллельное косоугольное проецирование и направление проецирования задаем параллельно образующим цилиндра s´ ‖ g Дополнительную плоскость проекций П´ совмещаем с плоскостью нижнего основания цилиндра. d 2≡П´ 2 Строим дополнительную проекцию Ф´ поверхности Ф, m´- линии m, l´- прямой l. d 2≡ Ф´ 1≡ m´ 1 Определяем точки K´ 11 , К´ 21 пересечения линии m´ 1 с l´ 1. {K´ 11 , К´ 21} = m´ 1 ∩ l´ 1 Строим горизонтальные и фронтальные проекции точек К 1 и К 2.

Пересечение прямой с сферической поверхностью

Задан шар. Определить точки К 1 и К 2 пересечения прямой l с поверхностью шара. Заключаем прямую l в плоскость Т. Т l Выбираем Т П 1. Следовательно: Т 1 ≡ l 1. Совмещаем фронтальную проекцию m 1 линии m – линии пересечения плоскости Т с поверхностью цилиндра, с фронтальной проекцией плоскости Т и прямой l. m 1 ≡ Т 1 ≡ l 1 Линия m – окружность, но ее фронтальная проекция имеет форму эллипса. Использование Т П 2 и m 2 ≡ Т 2 ≡ l 2 дает тот же результат. Следовательно, должна быть построена дополнительная проекция. Выбираем перемену плоскостей проекций. Дополнительную плоскость П 4 располагаем параллельно плоскости Т и перпендикулярно плоскости П 1. x 1, 4 ‖ (m 1 ≡ Т 1 ≡ l 1) На поле плоскости П 4 строим проекции прямой l и линии m. Определяем точки K 14 , К 24 пересечения линии m 4 с l 4. {K 14 , К 24} = m 4 ∩ l 4 Строим горизонтальные и фронтальные проекции точек К 1 и К 2.