Лекция 9 Построение элементарной геометрии на основе аксиоматики

Лекция 9 Построение элементарной геометрии на основе аксиоматики Вейля. Прямые и плоскости. Литература [1] § 81 ‑ 83, [2] § 12 ‑ 15. .

Основные объекты и основные отношения аксиоматики Вейля Основные объекты: R – множество действительных чисел, Ev 3 – элементы этого множества будем называть векторами и E 3 его элементы в дальнейшем называются точками. Основные отношения: операции сложения векторов, умножения вектора на число, скалярного произведения пары векторов; операция , ставящая в соответствие упорядоченной паре точек X, Y из E 3, вектор (X, Y) из Еv 3

Аксиомы линейного векторного пространства BI 1. Для любых векторов V 3 справедливо равенство . BI 2. Для любых трех векторов выполнено: . BI 3. Существует вектор V 3 такой, что для любого имеет место: BI 4. Для любого вектора V 3 найдется вектор V 3 такой, что . BI 5. Для любых чисел , R и любого вектора V 3 справедливо равенство ( + ) = + . BI 6. Для любого числа R и любых векторов и из V 3 справедливо равенство = . BI 7. Для любых чисел , R и любого вектора V 3 справедливо равенство ( ) = ( ). BI 8. Для любого вектора V 3 справедливо равенство 1 = .

Аксиомы размерности трехмерного векторного пространства V 3. BII 1. Существует линейно независимая тройка векторов , т. е. такая тройка векторов, для которой из соотношения следует = = =0. BII 2. Любые четыре вектора линейно зависимы, т. е. для любых векторов существуют числа , , , R, не все равные нулю, для которых .

Аксиомы скалярного произведения . BIII 1. Для любых чисел , R, и любых векторов справедливо равенство . BIII 2. Для любых векторов справедливо равенство BIII 3. Для любого ненулевого вектора имеет место неравенство . BIII 4. На пространстве V 3 задано множество положительно определенных симметрических билинейных форм, которое включает в себя скалярное произведение векторов, такое, что если , то , где положительное действительной число.

Аксиомы соответствия пар точек и векторов BIV 1. (Аксиома откладывания вектора) Для любой точки A Ev 3 и любого вектора существует единственная точка B Ev 3 такая, что . BIV 2. (Аксиома треугольника) Для любых трех точек A, B, C Ev 3 , справедливо равенство .

Теорема Если аксиоматика Гильберта трехмерного евклидова пространства непротиворечива, то справедливы утверждения аксиомы BI 1 – BIV 2 аксиоматики Вейля.

Непротиворечивость аксиоматики Вейля Аксиоматика Вейля трехмерного евклидова пространства непротиворечива, если непротиворечива арифметика.

Независимость аксиоматики Вейля Аксиоматика Вейля трехмерного евклидова пространства является независимой.

Определение прямой и плоскости Две точки А и В будут находиться в отношении (А В), в том и только в том случае, когда . Свойства отношения : рефлексивность, симметричность, транзитивность. Отношение является отношением эквивалентности Пусть дано одномерное векторное подпространство V 1 евклидова трехмерного векторного пространства E 3. Класс эквивалентности, определяемый отношением , соответствующим V 1, называется прямой пространства Ev 3. В случае, когда дано двумерное векторное подпространство V 2 пространства E 3, класс эквивалентности, определяемый отношением , соответствующим V 2, называется плоскостью пространства Ev 3.

Аксиомы принадлежности Утверждение I 1. Каковы бы ни были две точки А и В, существует прямая а, проходящая через эти две точки. Утверждение I 2. Каковы бы ни были две точки А и В, существует не более одной прямой а, проходящей через эти две точки. Утверждение I 3. На каждой прямой лежит, по крайней мере, две точки. Существует, по крайней мере, три точки, не принадлежащие одной прямой. Утверждение I 4. Каковы бы ни были три точки А, . В и С, не лежащие на одной прямой, существует плоскость , проходящая через эти три точки. На каждой плоскости лежит по крайней мере одна точка.

Аксиомы принадлежности (продолжение) Утверждение I 5. Каковы бы ни были три точки, не лежащие на одной прямой, существует не более одной плоскости, содержащей эти точки. Утверждение I 6. Если две точки А и В прямой а лежат в плоскости , то любая точка, принадлежащая прямой а, лежит в плоскости . Утверждение I 7. Если две плоскости и имеют общую точку А, то существует по крайней мере еще одна В, принадлежащая этим плоскостям. Утверждение I 8. Существует по крайней мере четыре точки, не лежащие в одной плоскости.

Аксиома параллельности Утверждение V 1. Пусть а – произвольная прямая, А – точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует не более одной прямой, проходящей через А и не пересекающей прямую а.

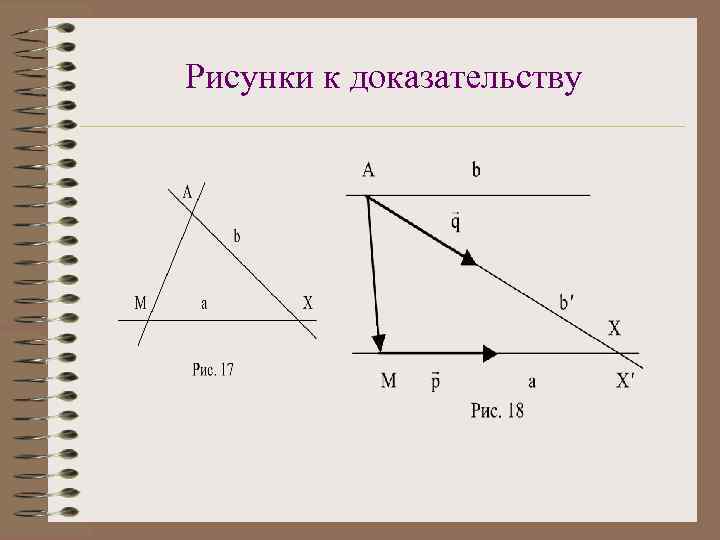Рисунки к доказательству

Определение понятия «лежать между» Пусть даны три различные точки А, В и С, принадлежащие одной прямой. Тогда под их простым отношением (АС, В) понимается число , удовлетворяющее условию. Пусть даны три различные точки А, В и С, принадлежащие одной прямой. Тогда точка В лежит между точками А и С (А-В-С), если простое отношение (АС, В) положительно

Утверждение II 1. Если точка В лежит между точками А и С, то А, В, С – три различные точки одной прямой, и при этом В лежит между С и А.

Утверждение II 2. Какова бы ни были точки А и В, существует по крайней мере одна точка С, такая, что В лежит между А и С.

Утверждение II 3. Среди любых трех точек прямой существует не более одной, лежащей между двумя другими.

Теорема о разбиении точек прямой точкой на два множества Пусть О – произвольная точка прямой l. Тогда она разбивает множество остальных точек прямой на два непустых подмножества так, что для любых двух точек А и В, принадлежащих одному подмножеству, точка О является внешней точкой отрезка АВ, а для любых двух точек C и D, принадлежащих различным подмножествам, точка О – внутренняя точка отрезка CD.

Теорема о разбиении плоскости прямой на два множества Прямая а, лежащая в плоскости , разделяет ее множество точек, не принадлежащих прямой, на два непустых подмножества, так, что если точки А и В принадлежат одному подмножеству, то отрезок АВ не имеет общих точек с прямой l, а если точки А и В принадлежат различным подмножествам, то отрезок АВ пересекает прямую l в своей внутренней точке.

Следствие Если дана прямая l и выбрана аффинная система координат так, чтобы ее начало, точка О, принадлежала прямой l, а вектор был ей параллелен, то полуплоскость, в которой лежит конец вектора , отложенный от начала О, характеризуется условием – вторые координаты ее точек положительны. Вторые же координаты точек другой полуплоскости отрицательны.

Утверждение. (Аксиома Паша) Пусть А, В и С – три точки, не лежащие на одной прямой, а l – прямая плоскости АВС, на проходящая через эти точки. Тогда, если прямая l проходит через точку отрезка АВ, то она содержит либо точку отрезка АС, либо точку отрезка ВС.

Угол, внутренние точки и лучи угла Под углом понимается пара лучей h и k, имеющие общее начало О и не лежащие на одной прямой. Если дан угол ОАВ, то через обозначим полуплоскость, граница которой совпадает с прямой Оа и которая содержит луч ОВ, а через - полуплоскость, граница которой совпадает с прямой ОВ и которая содержит луч ОА. Точки, принадлежащие пересечению полуплоскостей и , называются внутренними точками угла. Они образуют его внутреннюю область. Луч, вершина которого совпадает с вершиной угла, и все точки которого являются внутренними, мы называется внутренними лучом угла.

Лемма Пусть дан угол. Выберем аффинную систему координат плоскости так, чтобы ее начало совпадало с вершиной угла О, а векторы были, соответственно, направляющими векторами лучей ОА и ОВ. Тогда точка М является внутренней точкой угла в том и только в том случае, когда ее координаты относительно этой системы координат положительны.

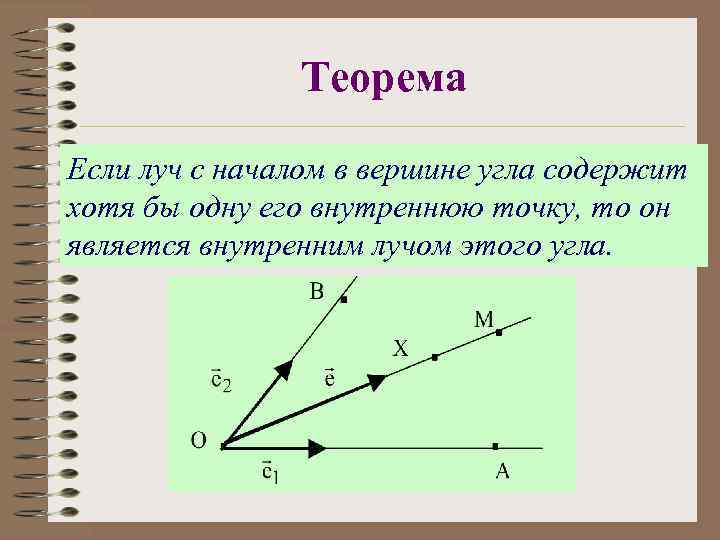Теорема Если луч с началом в вершине угла содержит хотя бы одну его внутреннюю точку, то он является внутренним лучом этого угла.

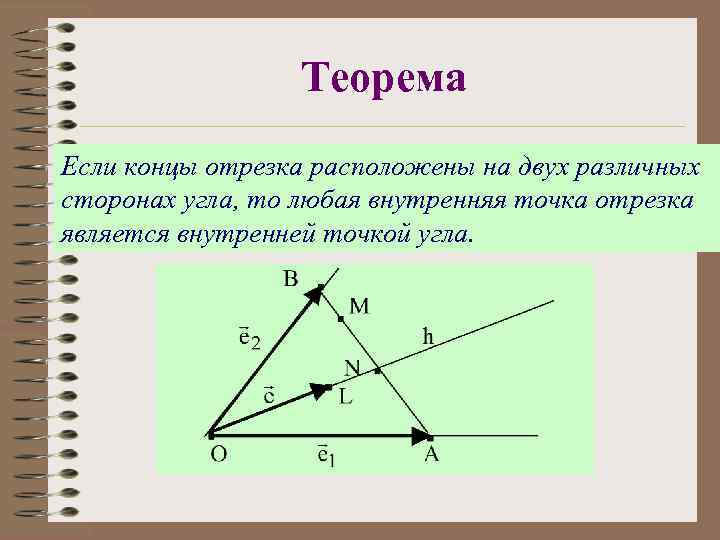Теорема Если концы отрезка расположены на двух различных сторонах угла, то любая внутренняя точка отрезка является внутренней точкой угла.

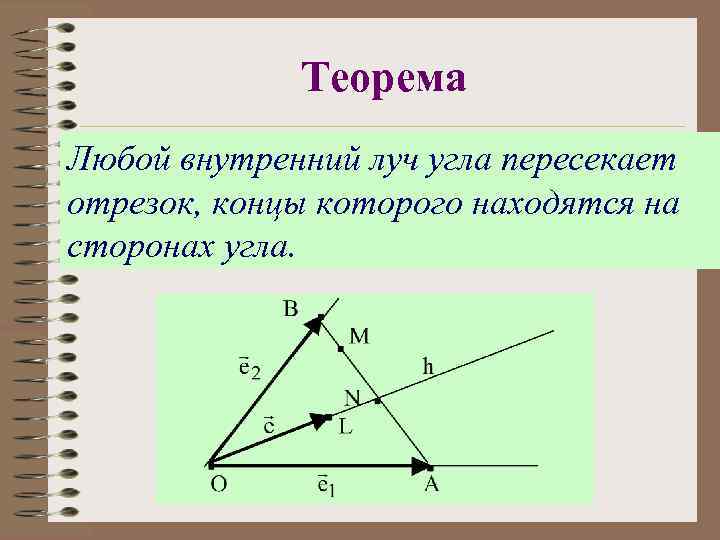Теорема Любой внутренний луч угла пересекает отрезок, концы которого находятся на сторонах угла.

Определение равенства отрезков Отрезки АВ и CD назовем конгруэнтными или равными, если равны скалярные произведения векторов Отрезки равны в том и только в том случае, когда равны квадраты длин векторов, соответствующих парам точек, определяемых концами отрезков. Так как длина вектора – положительное число, то равны и сами длины этих векторов. .

Утверждение III 1. Если дан отрезок АВ и луч с началом в точке A , то существует такая точка В этого луча, такая, что АВ = А В. Для каждого отрезка АВ требуется, чтобы АВ = ВА.

Утверждение III 2 Если отрезок АВ конгруэнтен отрезкам А В и А В , то отрезки А В конгруэнтны между собой. Доказательство этого утверждения непосредственно следует из определения 8. 1 и свойств равенства чисел

Утверждение III 3. Если точка В лежит между точками А и С, А-В-С, а точка В между точками А и С , А -В -С , и АВ = А В , ВС = В С , то АС = А С.

Определение равенства углов Индексом угла назовем число, равное: - направляющие векторы соответственно лучей h и k. Индекс угла не зависит от выбора направляющих векторов лучей h и k. Определение Два угла называются конгруэнтными или равными, если их индексы равны между собой. .

Утверждение III 4. Пусть дан угол и дан флаг ( ), то в полуплоскости существует один и только один луч k с началом в точке О , такой, что =. Каждый угол конгруэнтен сам себе.

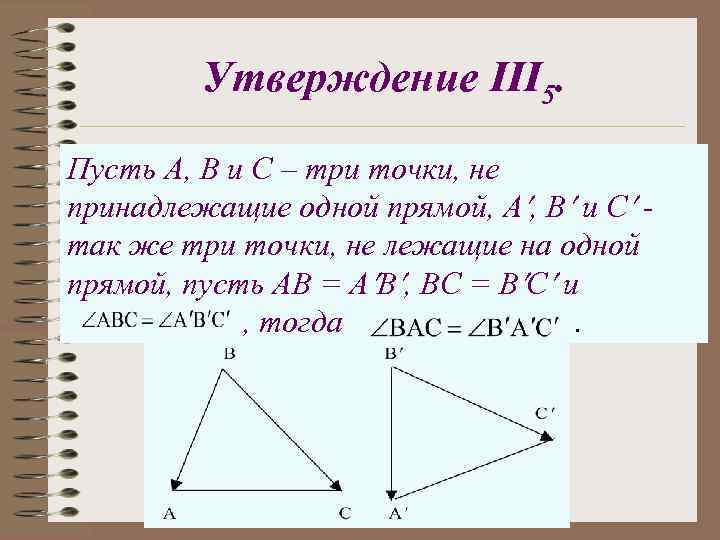Утверждение III 5. Пусть А, В и С – три точки, не принадлежащие одной прямой, А , В и С так же три точки, не лежащие на одной прямой, пусть АВ = А В , ВС = В С и , тогда.

Утверждение (Аксиома Архимеда). Пусть даны два отрезка АВ и CD. Тогда на прямой АВ существует такая конечная система, состоящая из n точек , расположенных так, что точка лежит между точками А и , точка - между точками и и так далее. При этом отрезки равны отрезку CD. Тогда точка В лежит между А и .

Утверждение (Аксиома Кантора). Пусть на произвольной прямой а дана бесконечная система отрезков , …, , … из которых каждый последующий лежит внутри предыдущего. Пусть далее, для любого отрезка CD найдется такой номер n, что . Тогда на прямой а существует такая точка Х, которая лежит внутри отрезков , , … …, и т. д. .

Равносильность аксиоматик Гильберта и Вейля, непротиворечивость аксиоматики Гильберта Аксиоматики Гильберта и Вейля трехмерного евклидова пространства эквивалентны. Аксиоматика Гильберта трехмерного евклидова пространства непротиворечива, если непротиворечива арифметика. Она также обладает свойством полноты.