ЛЕКЦИЯ 9. ОСОБЕННОСТИ

ЛЕКЦИЯ 9. ОСОБЕННОСТИ ПРИМЕНЕНИЯ ВЫБОРОЧНОГО МЕТОДА ОБСЛЕДОВАНИЯ. 1

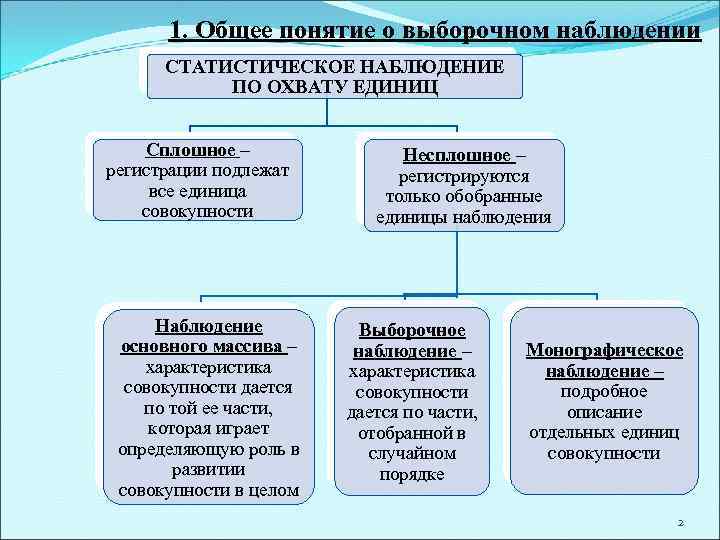
1. Общее понятие о выборочном наблюдении СТАТИСТИЧЕСКОЕ НАБЛЮДЕНИЕ ПО ОХВАТУ ЕДИНИЦ Сплошное – Несплошное – регистрации подлежат регистрируются все единица только обобранные совокупности единицы наблюдения Наблюдение Выборочное основного массива – наблюдение – Монографическое характеристика наблюдение – совокупности дается совокупности подробное по той ее части, дается по части, описание которая играет отобранной в отдельных единиц определяющую роль в случайном совокупности развитии порядке совокупности в целом 2

Выборочное наблюдение – это такое наблюдение, при котором обследованию подвергается часть единиц изучаемой совокупности, отобранных на основе научно разработанных принципов, обеспечивающих получение достаточного количества достоверных данных, для того чтобы охарактеризовать всю совокупность в целом. Основные требования, предъявляемые к статистическому наблюдению: ü информация должна быть достоверной, т. е. максимально соответствовать реальной действительности; ü сведения должны быть достаточно полными для решения задач исследования; ü отбор информации должен быть проведен в максимально сжатые сроки для использования ее в оперативных целях; ü денежные и трудовые затраты на организацию и проведение должны быть минимальными. 3

Генеральная совокупность - изучаемая совокупность единиц, подлежащая изучению по интересующим исследователя признакам. Выборочная совокупность - случайно выбранная из генеральной совокупности некоторая ее часть. Принципы отбора 1) обеспечение случайности - при отборе каждой из единиц изучаемой совокупности обеспечивается равная возможность попасть в выборку. 2) обеспечение достаточного числа отобранных единиц - связано с понятием репрезентативности выборки, т. е. при изучении лишь части генеральной совокупности полученные выводы можно применять ко всей совокупности. 4

Генеральная Выборочная Характеристика совокупность Объем совокупности (численность N n единиц) Численность единиц, обладающих М m обследуемым признаком Доля единиц, обладающих р= M / N w=m/n обследуемым признаком Средний размер признака Дисперсия признака Среднее квадратическое отклонение 5

2. Ошибки выборочного наблюдения Сделать вывод о том, насколько попавшие в выборку единицы наблюдения могут представлять генеральную совокупность, позволяют ошибки репрезентативности: 1. Средняя ошибка выборки ( µ ) - характеризует среднюю величину возможных расхождений выборочной и генеральной средней (или доли) и представляет собой по форме и содержанию среднее квадратическое отклонение возможных значений выборочной средней от генеральной. 2. Предельная ошибка выборки (Δ) - разность между величиной средней в генеральной совокупности и ее величиной, вычисленной по результатам выборочного наблюдения. Предельная ошибка рассчитывается: Δ = t µ , где t – коэффициент доверия (коэффициен кратности), то есть показатель, зависящий от вероятности p, с которой рассчитывается предельная ошибка, находится по таблице - удвоенной функции Лапласа. 6

Средняя ошибка выборки находится: ü В прямой зависимости от дисперсии изучаемого признака в генеральной совокупности (чем больше разброс единиц в генеральной совокупности, тем больше ошибка выборки); ü В обратной зависимости от объема выборки (чем больше объем выборочной совокупности, тем меньше ошибка выборки). Предельная ошибка выборки находится: ü Величины средней ошибки выборки; ü Уровня вероятности, который гарантирует, что генеральная средняя не выйдет за указанные пределы. 7

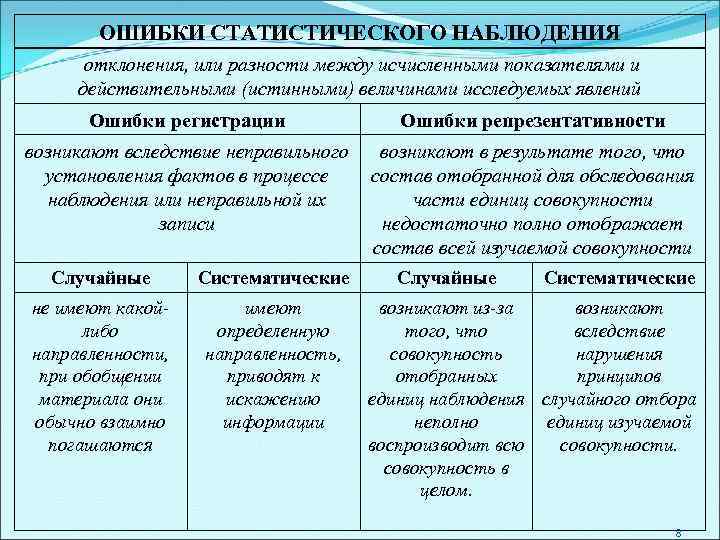
ОШИБКИ СТАТИСТИЧЕСКОГО НАБЛЮДЕНИЯ отклонения, или разности между исчисленными показателями и действительными (истинными) величинами исследуемых явлений Ошибки регистрации Ошибки репрезентативности возникают вследствие неправильного возникают в результате того, что установления фактов в процессе состав отобранной для обследования наблюдения или неправильной их части единиц совокупности записи недостаточно полно отображает состав всей изучаемой совокупности Случайные Систематические Случайные Систематические не имеют какой- имеют возникают из-за возникают либо определенную того, что вследствие направленности, направленность, совокупность нарушения при обобщении приводят к отобранных принципов материала они искажению единиц наблюдения случайного отбора обычно взаимно информации неполно единиц изучаемой погашаются воспроизводит всю совокупности. совокупность в целом. 8

3. Формирование выборочной совокупности 1. Бесповторный отбор - попавшая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор. При этом объем генеральной совокупности по мере формирования выборки уменьшается. 2. Повторный отбор - попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в исходную (генеральную) совокупность для участия в дальнейшей процедуре отбора. В этом случае объем генеральной совокупности остается постоянным, что упрощает формулы ошибок. Метод отбора определяет конкретный механизм выборки единиц из генеральной совокупности и подразделяется на: ü собственно случайный; ü механический; ü типический; ü серийный; ü комбинированный. 9

3. 1. Простая случайная выборка. Выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки. Организуется таким образом, чтобы у всех единиц генеральной совокупности были равные возможности попасть в выборку. Сделать вывод о том, насколько попавшие в выборку единицы наблюдения могут представлять генеральную совокупность, позволяют ошибки репрезентативности: средняя и предельная ошибки выборки. 10

Средняя ошибка в условиях большой выборки (n>30) Способ отбора единиц повторный бесповторный Средняя ошибка для средней для доли 11

Средняя ошибка в условиях большой выборки Способ отбора единиц повторный бесповторный Средняя ошибка для средней для доли Предельная ошибка для средней для доли 12

Формулы предельной ошибки позволяют решать задачи трех видов: 1. Определение пределов генеральных характеристик с заданной степенью надежности (доверительной вероятностью) на основе показателей, полученных по данным выборки. Доверительные интервалы для генеральной средней: Доверительные интервалы для генеральной доли: 13

Формулы предельной ошибки позволяют решать задачи трех видов: 2. Определение доверительной вероятности того, что генеральная характеристика может отличаться от выборочной не более чем на определенную заданную величину. Доверительная вероятность является функцией от t, определяемой по формуле: По величине t определяется доверительная вероятность. 14

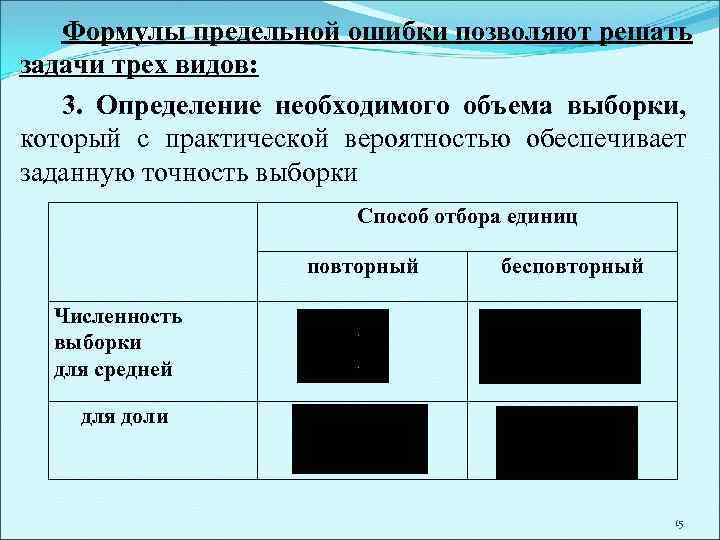
Формулы предельной ошибки позволяют решать задачи трех видов: 3. Определение необходимого объема выборки, который с практической вероятностью обеспечивает заданную точность выборки Способ отбора единиц повторный бесповторный Численность выборки для средней для доли 15

3. 2. Механическая выборка. Заключается в отборе единиц из генеральной совокупности через равные промежутки времени из определенного расположения их в генеральной совокупности, например, по алфавиту. Задачи: 1) определение «шага отчета» (расстояния между отбираемыми единицами) – определяется путем деления численности генеральной совокупности на численность выборочной совокупности; 2) выбор единицы, с которой надо начинать отчет – рекомендуется производить путем случайного отбора из единиц первого интервала – первого «шага отчета» . Если в генеральной совокупности единицы располагаются случайным образом по отношению к изучаемому признаку, то механический отбор можно рассматривать как разновидность случайного отбора, поэтому для оценки ошибки механической выборки применяются формулы случайной выборки. 16

3. 3. Типическая выборка. Генеральная совокупность вначале расчленяется на однородные типические группы. По каждой группе определяются ее объем ( N) и число подлежащих наблюдению единиц (n). Общее число единиц выборочной совокупности распределяется между группами пропорционально численности групп в составе генеральной совокупности. Такой отбор называется пропорциональным. , где N – общая численность единиц в генеральной совокупности - численность отдельных групп генеральной совокупности, n – общий объем выборочной совокупности. 17

3. 3. Типическая выборка. Кроме пропорционального размещения применяется оптимальное размещение, при котором число наблюдений в группе определяется по формуле: 18

Условные обозначения - средняя групповая выборочная дисперсия средней; - внутригрупповая дисперсия данной (i-ой) группы в выборочной совокупности; - средняя групповая выборочная дисперсия доли; Предельная (максимально возможная) ошибка типической выборки: ; 19

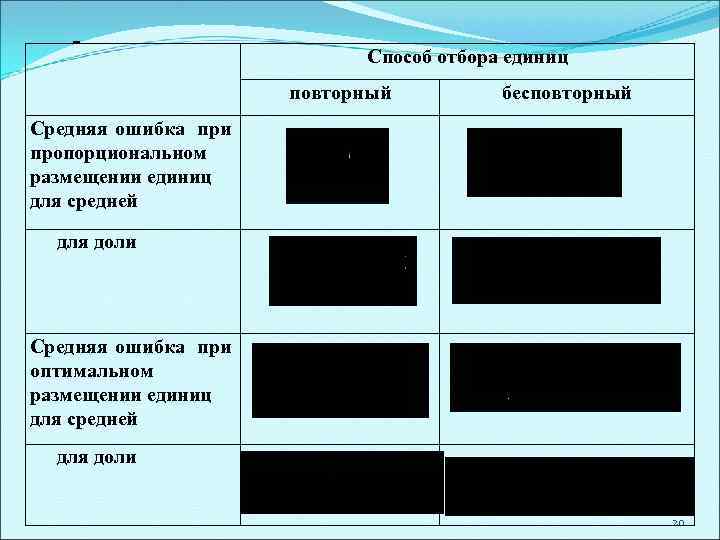
Способ отбора единиц повторный бесповторный Средняя ошибка при пропорциональном размещении единиц для средней для доли Средняя ошибка при оптимальном размещении единиц для средней для доли 20

3. 4. Серийный или гнездовой отбор. Случайный выбор групп единиц с последующим сплошным наблюдением внутри отобранных серий. Способ отбора единиц повторный бесповторный Средняя ошибка для средней для доли 21

Условные обозначения - межгрупповая выборочная дисперсия средней; - средний уровень признака в серии; - средний уровень признака для всей выборочной совокупности; m - число равных серий в выборочной совокупности; M - число равных серий в генеральной совокупности; - межгрупповая выборочная дисперсия доли; - доля единиц, обладающих данным признаком в серии; - доля единиц, обладающих данным признаком во всей выборочной совокупности 22

3. 5. Комбинированный отбор. Предполагает использование нескольких способов выборки. Можно комбинировать, например, серийную выборку и случайную. В этом случае, разбив генеральную совокупность на серии (группы) и отобрав нужное число серий, производят случайную выборку единиц в серии. Такая комбинированная выборку может быть повторной и бесповторной. Средняя ошибка определяется по формуле: При повторном отборе: При бесповторном отборе: 23

4. Малая выборка. Выборочное наблюдение, численность единиц которого не превышает 30. Разработка теории малой выборки была начата английским статистиком В. С. Госсетом (печатавшимся под псевдонимом Стьюдент). Он доказал, что оценка расхождения между средней малой выборки и генеральной средней имеет особый закон распределения. Предельная ошибка малой выборки определяется по формуле: Средняя ошибка малой выборки: , где - дисперсия малой выборки. - среднее значение признака по выборке; n-1 – число степеней свободы t - коэффициент доверия малой выборки, зависящей не только от заданной доверительной вероятности, но и от численности единиц выборки. 24

5. Способы распространения характеристик выборки на генеральную совокупность. Способ прямого пересчёта. Применяется для определения по данным о выборочной доле величины интервала, в пределах которого в генеральной совокупности с заданной вероятностью находится число единиц, обладающих изучаемым признаком. Он состоит в том, что показатели выборочной доли или средней распространяется на генеральную совокупность с учётом ошибки выборки. Способ поправочных коэффициентов. Применяется в случаях, когда целью выборочного метода является уточнение результатов сплошного учета. Основное назначение метода поправочных коэффициентов – уточнение данных сплошного массового наблюдения посредством выборочных проверок. 25