Лекция 9 23 04 2012 Информационные системы

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Управление инвестиционными процессами, связанными с вложениями денежных средств в долгосрочные материальные и финансовые активы, представляет собой сложный процесс, поскольку принимаемые решения: 1. рассчитаны на длительные периоды времени; 2. являются частью стратегии развития фирмы в перспективе; 3. влекут за собой значительные оттоки средств; 4. с определенного момента времени могут стать необратимыми; 5. опираются на прогнозные оценки будущих затрат и доходов. 1

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Одним из ключевых моментов принятии инвестиционных решений является оценка эффективности предполагаемых капиталовложений. Совокупность методов, применяемых для оценки эффективности инвестиций, подразделяется на две группы: динамические (учитывающие временной фактор) и статические. 2

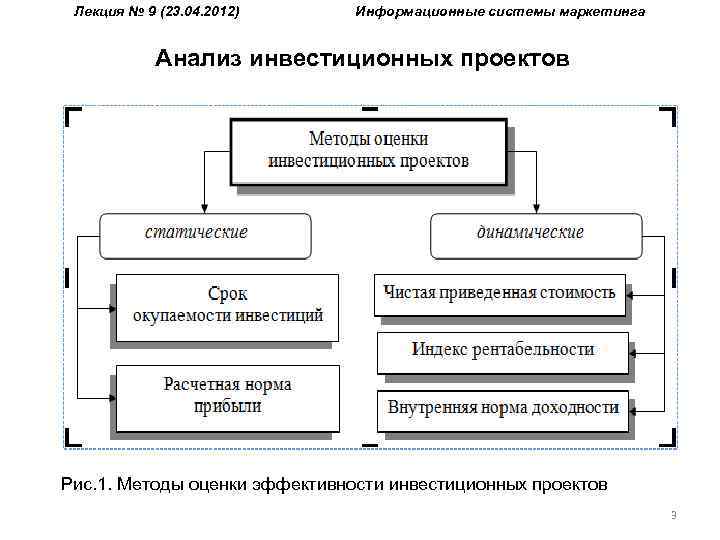Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Рис. 1. Методы оценки эффективности инвестиционных проектов 3

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Динамические методы позволяют учесть фактор времени, они отражают современные подходы к оценке эффективности инвестиций и преобладают в практике крупных и средних предприятий развитых стран. В хозяйственной практике России применение этих методов обусловлено также и все еще сравнительно высоким уровнем инфляции. Эти методы являются более точными и используются при более детальном рассмотрении проектов, тогда как методы, основанные на учетных оценках (статические методы), используются в основном для экспресс-оценки. 4

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Динамические методы часто называют дисконтными, поскольку они базируются на определении современной величины (т. е. на дисконтировании) денежных потоков, связанных с реализацией инвестиционного проекта. При этом делаются важные допущения: 1. потоки денежных средств на конец (начало) каждого периода реализации проекта известны; 2. определена оценка, выраженная в виде процентной ставки (нормы дисконта), в соответствии с которой средства могут быть вложены в данный проект. 5

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Метод чистой приведенной стоимости (NPV). Основная идея заключается в том, чтобы найти разницу между инвестиционными затратами и будущими доходами, выраженную в скорректированной во времени (как правило, к моменту начала реализации проекта) денежной величине. При заданной норме дисконта можно определить современную величину всех оттоков и притоков денежных средств в течение срока экономической жизни проекта, а также сопоставить их друг с другом. 6

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Результатом такого сопоставления будет положительная или отрицательная величина (чистый приток или чистый отток денежных средств), показывающая, удовлетворяет или нет проект принятой норме дисконта. В простейшем случае денежный поток проекта состоит из первоначальных инвестиций I 0 и последующих поступлений средств от его реализации CFt. 7

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Чистая приведенная стоимость вычисляется по формуле: где PV — приведенная стоимость денежного потока на протяжении экономической жизни проекта. Величину PV определяем по формуле: где r — норма дисконта; n — число лет реализации проекта; СFt — чистый поток платежей в периоде t (чистый кэш-флоу или поток наличности). 8

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов NPV определяем по формуле: Если NPV>0, это означает, что в течение своей экономической жизни проект возместит первоначальные затраты I 0, обеспечит получение прибыли согласно заданному стандарту r, а также ее некоторый резерв, равный NPV. Отрицательная NPV показывает, что заданная норма прибыли не обеспечивается и проект убыточен. При NPV = 0 проект только окупает произведенные затраты, но не приносит дохода. 9

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Общее базовое правило NPV: если NPV > 0, то проект принимается, иначе, его следует отклонить. Использование критерия NPV теоретически обоснованно, и в целом он считается наиболее корректной мерой эффективности инвестиций. Вместе с тем применение абсолютных показателей при анализе проектов с различными исходными условиями (первоначальными инвестициями, сроками экономической жизни и др. ) может приводить к затруднениям принятии управленческих решений. 10

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Поэтому наряду с абсолютным показателем эффективности инвестиций NPV используется также и относительные — индекс рентабельности и внутренняя норма доходности. Индекс рентабельности проекта PI показывает, сколько единиц современной величины денежного потока приходится на единицу предполагаемых первоначальных затрат. Для расчета этого показателя используется формула: где опять I 0 — сумма инвестиций на начало проекта; PV — приведенная стоимость денежного потока на протяжении экономической жизни проекта. 11

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Если критерий PI > 1, то современная стоимость денежного потока проекта превышает первоначальные инвестиции, обеспечивая тем самым наличие положительной величины NPV — чистой приведенной стоимости. При этом рентабельность превышает заданную норму и проект следует принять. При PI = 1 величина чистой современной стоимости NPV равна 0 и инвестиции не приносят дохода. Если PI < 1, проект не обеспечивает заданного уровня рентабельности и его следует отклонить. 12

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Базовое правило для PI: если PI > 1, то проект принимается, иначе — его следует отклонить. Обычно расчет индекса рентабельности дополняет расчет NPV с целью отбора проектов, порождающих максимальную современную стоимость на единицу затрат. Внутренняя норма доходности IRR — это наиболее широко используемый критерий эффективности инвестиций. Под внутренней нормой доходности понимают процентную ставку, при которой чистая современная стоимость инвестиционного проекта равна нулю. 13

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Внутренняя норма доходности определяется из уравнения: Уравнение решается относительно IRR какимлибо итерационным методом. Нетрудно заметить, что при NPV = 0 современная стоимость проекта (PV) равна по абсолютной величине первоначальным инвестициям I 0, следовательно, они окупаются. В общем случае, чем выше IRR, тем больше эффективность инвестиций. 14

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов На практике IRR сравнивается с заданной нормой дисконта r. При этом если IRR > r, проект обеспечивает положительную NPV и доходность, равную IRR – r. Если IRR < r, затраты превышают доходы, и проект будет убыточным. Общее правило IRR: если IRR > r, то проект принимается, иначе его следует отклонить. 15

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Анализ инвестиционных проектов Расчет вручную показателей, базирующихся на дисконтных методах, особенно NPV и IRR, достаточно трудоемок. Однако табличные процессоры позволяют быстро и эффективно выполнить эти расчеты с помощью специальной группы финансовых функций, предназначенных для автоматизации анализа эффективности инвестиционных проектов. 16

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Для расчета чистой приведенной стоимости потока платежей в Excel реализовано две функции — ЧПС и ЧИСТНЗ. В Calc их аналоги называются NPV и XNPV. 17

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Эти функции используют следующие аргументы: ставка, процент — норма дисконта (процентная ставка); значения — значения элементов денежного потока; даты — даты платежей (только для ЧИСТНЗ). Рассмотрим технологию применения этих функций для расчета NPV. ЧПС позволяет определить чистую приведенную стоимость потока равномерно распределенных по времени платежей PV с учетом заданной оценки. 18

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Следует обратить внимание на то, что функция не учитывает величину первоначальных затрат I 0, то есть инвестиций, сделанных на момент времени t = 0. Поэтому для определения показателя чистой приведенной стоимости (NPV) из полученного результата следует вычесть размер первоначальных вложений I 0. При проведении анализа с применением функции ЧПС I 0 удобно задавать как отрицательную величину. Тогда показатель NPV рассчитывается по формуле: NPV = I 0 + PV, I 0 < 0. 19

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Пример 1. Фирма собирается вложить средства в приобретение нового оборудования, стоимость которого вместе с доставкой и установкой составит 100 000 руб. Ожидается, что внедрение оборудования обеспечит получение на протяжении 6 лет чистых доходов в 25 000, 30 000, 35 000, 40 000, 45 000 и 50 000 руб. соответственно. Принятая норма дисконта равна 10%. Определить экономическую эффективность проекта. 20

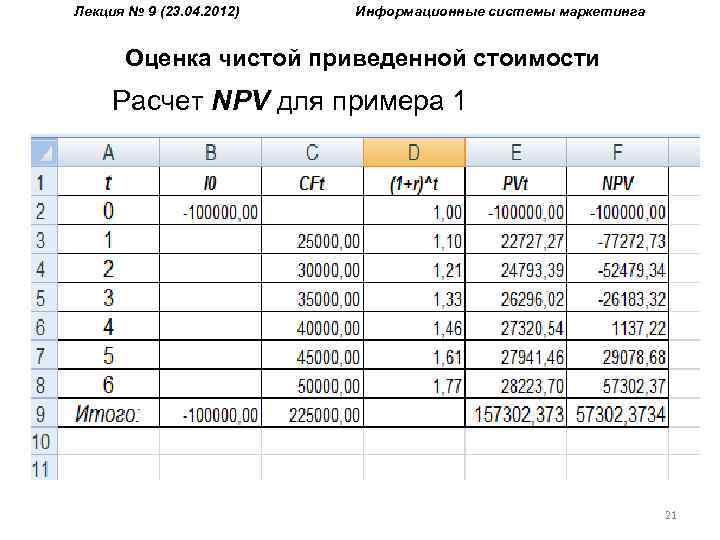Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Расчет NPV для примера 1 21

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости При условии правильной оценки денежного потока проект обеспечивает возмещение произведенных затрат (примерно к концу 4 -го года) и получение 10% чистой прибыли, а также дополнительной (сверх установленной нормы) прибыли, равной величине NPV (57 302 руб. ) в F 10. Другое объяснение полученного показателя NPV: если проект финансировался за счет долгосрочной ссуды в 100 000 руб. , взятой на 6 лет под 10% годовых, то ее величина и проценты могли бы быть полностью выплачены из поступлений наличности от проекта. Кроме того, после расчетов с кредиторами остаток полученной от проекта наличности составил бы сумму в 57 302. 37 руб. 22

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости При прогнозировании потоков платежей по периодам должны учитываться все виды поступлений и выплат, связанных с данным проектом, как производственного, так и непроизводственного характера. Амортизационные отчисления, поступления от ликвидации либо продажи оборудования по окончанию проекта должны включаться в доходы соответствующих периодов. Гораздо проще рассчитать показатели экономической эффективности проекта с помощью финансовых функций. В Calc воспользуемся формулой в F 11: =NPV(C 1; C 5: C 10)+B 4. Можно констатировать совпадение результатов. 23

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Пример 2. После начальных инвестиций начата реализация проекта. В последующие три года ожидаются доходы 3000 у. е. , 4200 у. е. , 6800 у. е. Издержки привлечения капитала составляют 10%. Рассчитать чистую приведенную стоимость проекта при начальных инвестициях в проект: а) 10000 руб. , б) 20000 руб. , в) 5000 руб. 24

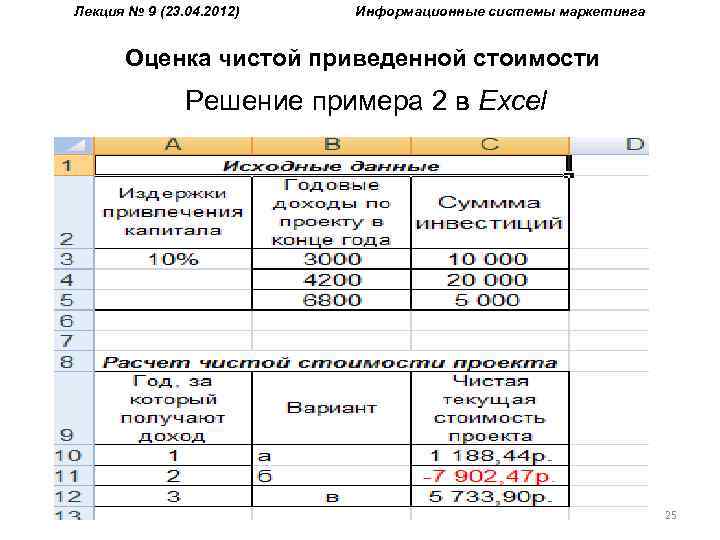Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Решение примера 2 в Excel 25

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Для удобства расчетов и в Excel и в Calc целесообразно комбинировать абсолютный и относительный способы адресации ячеек. Полученные результаты подтверждают очевидное соображение, что наибольшую чистую современную стоимость имеет вариант проекта, при котором начальные инвестиции будут минимальны (5000 у. е. ). Отрицательное значение чистой современной стоимости, полученное для варианта б, характеризует его как абсолютно неэффективный для вложения денежных средств. 26

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Пример 3. По инвестиционному проекту предполагается, что после затрат в начальный момент его реализации, ожидаемые доходы за первые пять лет составят 8000 руб. , 9200 руб. , 10000 руб. , 13900 руб. и 14500 руб. соответственно. На 6 -ой год ожидается убыток в 5000 руб. Цена капитала считается постоянной и равной 8% годовых. 27

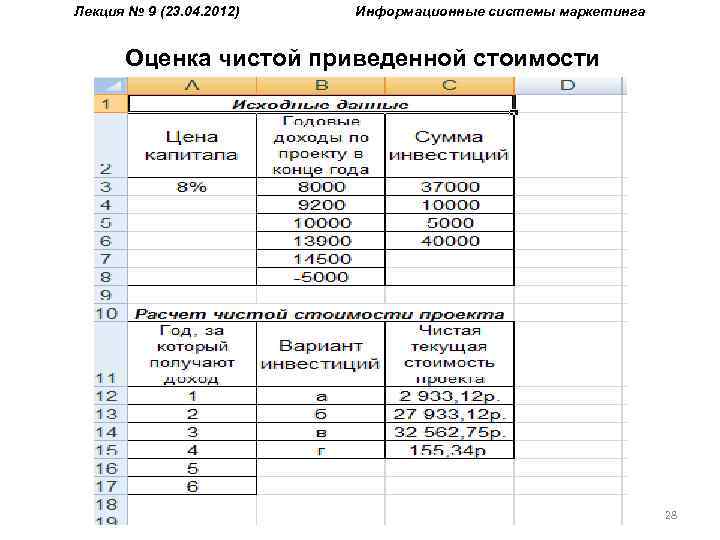Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости 28

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Итак, наибольшую чистую приведенную стоимость имеет вариант в). Низкое значение чистой приведенной стоимости, полученное для варианта г), характеризует данный проект как наименее эффективный из 4 сопоставляемых для вложения денежных средств. Однако положительное значение этого показателя дает возможность не исключать этот проект из инвестиционного портфеля фирмы. Вместе с тем, практическое применение функции ЧПС ограничено случаем равномерного распределения платежей во времени. 29

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Данное ограничение позволяет преодолеть ЧИСТНЗ (XNPV). Она позволяет определить показатель NPV для потоков с платежами произвольного размера, осуществляемых за любые промежутки времени. Для каждого платежа должна быть указана предполагаемая дата его осуществления. Кроме того, в отличие от ЧПС (NPV), ее продвинутый аналог ЧИСТНЗ (XNPV) корректно учитывает величину первоначальных инвестиций I 0 и позволяет рассчитать NPV напрямую, без выполнения дополнительных действий. 30

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Пример 4. Вложение на дату 12. 03. 2004 суммы в 1000 ден. ед. обеспечивает получение 02. 07. 2004 суммы в 500 и 23. 08. 2005 суммы в 700 ден. ед. Необходимо определить эффективность операции при норме дисконта в 10%. Непосредственно как третий аргумент функции даты введены быть не могут, так как ЧИСТНЗ работает с порядковыми номерами дат. По умолчанию отсчет начинается с 1 января 1900 г. Изменив тип ячеек с Дата на Общий, можно узнать, что перечисленные в задании даты имеют числовые коды 38058, 38170, 38587. 31

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Несомненно, было бы крайне неудобно оформлять вызов функции в виде: =ЧИСТНЗ(0, 1; 500; 700; {38058; 38170; 38587) Проблема заключается в сложности определения порядковых номеров дат вручную. Существуют два пути ее решения: • использование функций для преобразования дат; • задание аргументов в виде адресов содержащих их ячеек. Первый способ основан на возможности использования функции ДАТА (год; месяц; день). Однако при большом числе платежей формула станет слишком длинной и малопонятной. 32

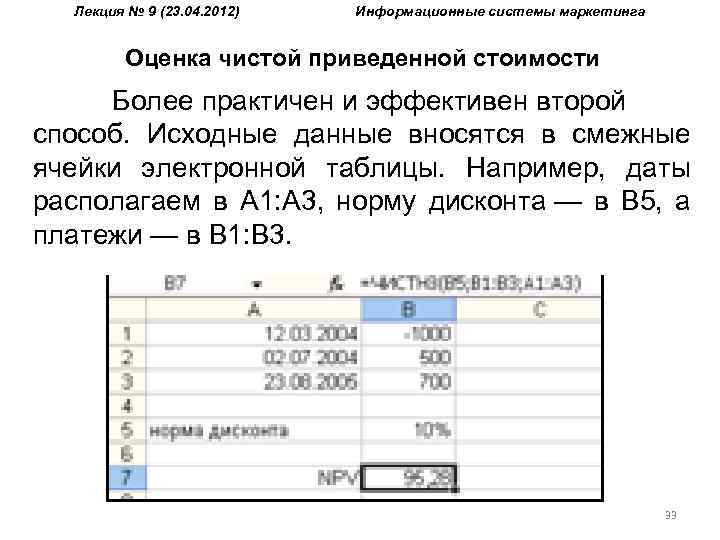Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Более практичен и эффективен второй способ. Исходные данные вносятся в смежные ячейки электронной таблицы. Например, даты располагаем в А 1: А 3, норму дисконта — в B 5, а платежи — в В 1: В 3. 33

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости Эксперименты показывают, что в целом показатель NPV должным образом отражает соотношение между притоками и оттоками денежных средств в течение определенного периода времени, а также дает представление как о возмещении произведенных затрат, так и о достижении нормы доходности вложения средств. Являясь абсолютным показателем, NPV обладает важнейшим свойством — свойством аддитивности (NPV различных проектов можно суммировать): NPV(А, В, С) = NPV(А) + NPV(B) + NPV(С). 34

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Оценка чистой приведенной стоимости К числу других важнейших свойств этого критерия следует отнести более реалистические предположения о ставке реинвестирования поступающих средств. В методе NPV неявно предполагается, что средства, поступающие от реализации проекта, реинвестируются по заданной норме дисконта. Реинвестирование — использование полученной в результате предпринимательской деятельности прибыли для новых инвестиций. 35

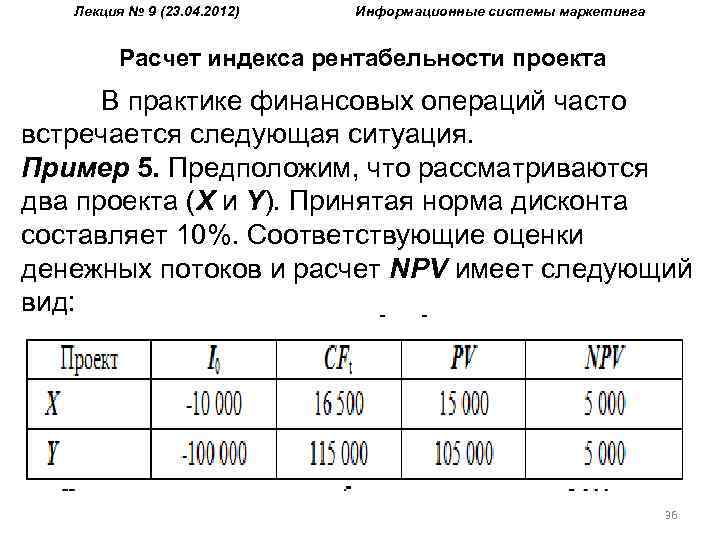Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет индекса рентабельности проекта В практике финансовых операций часто встречается следующая ситуация. Пример 5. Предположим, что рассматриваются два проекта (X и Y). Принятая норма дисконта составляет 10%. Соответствующие оценки денежных потоков и расчет NPV имеет следующий вид: 36

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет индекса рентабельности проекта Чистая современная стоимость обоих проектов составляет 5 000 и в случае необходимости выбора не позволяет однозначно определить лучший вариант. Поэтому наряду с абсолютным показателем эффективности инвестиций NPV используется также и относительные — индекс рентабельности и внутренняя норма доходности. Рассчитаем индексы рентабельности для вышеприведенного примера. PI(X) = 15 000 / 10 000 = 1. 50; PI(Y) = 105 000 / 100 000 = 1. 05. 37

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет индекса рентабельности проекта Таким образом, проект X обеспечивает большую рентабельность инвестиций и, в случае невозможности одновременной реализации обоих проектов, ему следует отдать предпочтение. Хотя ни в Exсel, ни в Calc нет специальной функции для вычисления индекса рентабельности, он легко определяется. Применение показателя PI часто бывает полезным в случае, когда существует возможность финансирования нескольких проектов, но при этом инвестиционный бюджет фирмы ограничен. 38

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет индекса рентабельности проекта Индекс рентабельности не всегда обеспечивает однозначную оценку эффективности инвестиций, и проект с наиболее высоким PI не обязательно соответствует проекту с самой высокой NPV. В частности, использование индекса рентабельности может привести к ошибочным результатам при оценке взаимоисключающих проектов. 39

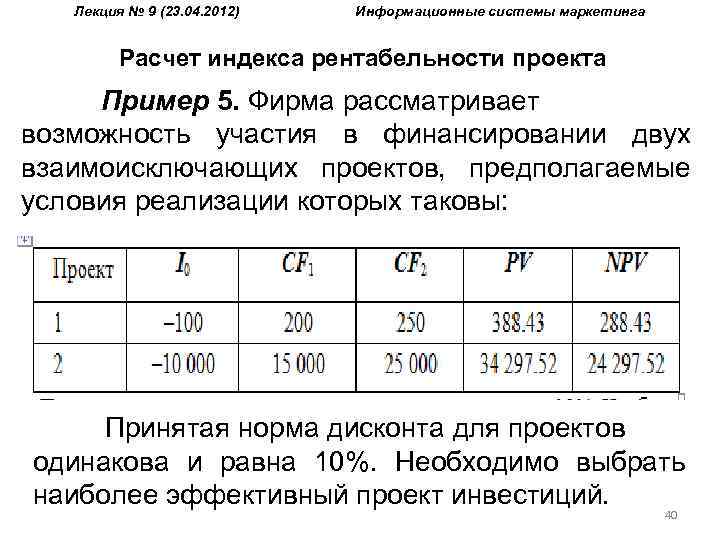Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет индекса рентабельности проекта Пример 5. Фирма рассматривает возможность участия в финансировании двух взаимоисключающих проектов, предполагаемые условия реализации которых таковы: Принятая норма дисконта для проектов одинакова и равна 10%. Необходимо выбрать наиболее эффективный проект инвестиций. 40

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет индекса рентабельности проекта Определим индексы рентабельности для проектов 1 и 2: PI 1 = (288. 43/100) + 1 = 3. 88; PI 2 = (24297. 52/10000) + 1 = 3. 43. Нетрудно заметить, что при наличии у фирмы соответствующих средств второй проект предпочтительнее, так как он генерирует большую NPV. Однако индекс рентабельности «отдает» предпочтение первому проекту. Поэтому обычно расчет индекса рентабельности дополняет расчет NPV с целью отбора проектов, порождающих максимальную современную стоимость на единицу затрат. 41

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет внутренней нормы доходности IRR вручную достаточно сложен. Однако современные табличные процессоры позволяют быстро определить этот показатель путем использования специальных функций: 42

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет внутренней нормы доходности 1. 2. 3. 4. 5. Функции используют следующие аргументы: значения — массив элементов денежного потока, которые соответствуют расписанию выплат; ставка_финанс — норма дисконта; ставка_реинвест — ставка реинвестирования (процентная ставка, начисляемая на денежные суммы при их реинвестировании); даты — даты платежей (расписание выплат); предположение, предп, прогноз — предполагаемый результат (необязательный аргумент для ускорения сходимости итерационного алгоритма). 43

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет внутренней нормы доходности Для корректной работы денежный поток должен состоять из хотя бы одного отрицательного и одного положительного элемента (то есть должны иметь место хотя бы одна выплата и одно поступление средств). Рассчитаем внутреннюю норму доходности для примера 5 с помощью функции ВСД (IRR). Поскольку полученный результат превышает норму дисконта (10%), критерий IRR также рекомендует принять данный проект. При этом эффективность данной операции составит: 25. 5% – 10% = 15. 5%. 44

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет внутренней нормы доходности Критерий внутренней нормы доходности несет в себе также информацию о приблизительной величине предела безопасности для проекта. Если предположить, что в предыдущем случае при оценке денежного потока возможна ошибка и IRR проекта окажется равной 20%, при прежней процентной ставке по кредиту (10%) проект все равно обеспечит получение дохода. 45

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет внутренней нормы доходности При повышении стоимости займа до 22– 24% при IRR = 26% остается слишком малый предел безопасности на случай ошибки и, возможно, такой проект будет сразу отвергнут, а проведение дальнейшего анализа не потребуется. Таким образом и Exсel, и Calc позволяют быстро и эффективно осуществить анализ предела безопасности для инвестиционных проектов. Рассмотренные достоинства критерия IRR объясняют его популярность на практике. Исследования зарубежного опыта показывают, что более 40% фирм используют этот критерий для оценки эффективности инвестиций. 46

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет внутренней нормы доходности Вместе с тем его недостатки также требуют серьезного рассмотрения. К одному из наиболее существенных следует отнести нереалистичное предположение о ставке реинвестирования. В отличие от NPV критерий внутренней нормы доходности неявно предполагает реинвестирование получаемых доходов по ставке IRR. Если финансирование проекта в примере 5 осуществляется за счет банковской ссуды под 10% годовых, то получаемые в процессе его реализации доходы должны быть реинвестированы по ставке 25. 5% годовых, то есть в 2. 55 раза превышающей ставку по долгосрочным кредитам. Очевидно, что это вряд ли осуществимо в реальной практике. 47

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет внутренней нормы доходности Для корректного учета предположения о реинвестировании в Exсel реализована функция МВСД (MIRR), вычисляющая модифицированную внутреннюю норму доходности. Данная функция имеет специальный аргумент — предполагаемую ставку реинвестирования. Предположим, что в примере 5 имеется возможность реинвестирования получаемых доходов по ставке 8% годовых. Тогда модифицированная внутренняя норма доходности составит 17. 7% 48

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет внутренней нормы доходности Нетрудно заметить, что модифицированная норма рентабельности оказалась почти на треть ниже, однако все же выше заданной, поэтому даже при более пессимистичной оценке внешних условий проект можно считать прибыльным. Варьируя значение ставки реинвестирования, легко проследить изменения IRR. Второй недостаток показателя внутренней нормы доходности связан с возможностью существования его нескольких значений. В общем случае, если анализируется единственный или несколько независимых проектов с «обычным» денежным потоком (то есть после первоначальных затрат следуют положительные притоки денежных средств), применение критерия IRR всегда приводит к тем же результатам, что и NPV. 49

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Расчет внутренней нормы доходности Однако, в случае чередования притоков и оттоков наличности (например, в случае капитального ремонта или модернизации оборудования) для одного проекта могут существовать несколько значений IRR. Самое простое в такой ситуации — руководствоваться наименьшим значением IRR среди полученных. Вместе с тем самым рациональным подходом к оценке эффективности долгосрочных инвестиций будет применение всех рассмотренных показателей, так как различные способы оценки обеспечивают лиц, принимающих решения, более полной информацией. 50

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов Применение электронных таблиц позволяет быстро определить значения всех необходимых критериев оценки проектов и провести анализ чувствительности. Вместе с тем, попытка создать универсальный шаблон для анализа инвестиций связана с рядом проблем, порождаемых, прежде всего, индивидуальными особенностями каждого конкретного проекта. Методика разработки шаблона, позволяющего автоматизировать процесс расчета основных критериев эффективности инвестиций: 51

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов 52

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов Первая часть (блок А 1: В 4) предназначена для ввода условий реализации проекта: принятой нормы дисконта — r, срока реализации — n, предполагаемой ставки реинвестирования — r 1. Вторая часть таблицы предназначена для исходных данных — потока платежей. Она состоит из двух граф: дата платежа и его сумма. Поскольку заранее неизвестно распределение потока платежей для того или иного проекта, эта часть таблицы пока состоит из двух строк, позволяющих задать минимально возможный поток. 53

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов Такой поток состоит из начальных инвестиций (В 7) и последнего (возможно единственного) поступления средств (В 8). Соответственно ячейки А 7: А 8 предназначены для хранения дат платежей минимального потока. Перед тем как приступить к дальнейшему проектированию второй части модели, полезно определить собственные имена для ячеек, в которые будут вводиться исходные данные. Например, ячейкам А 7: А 8 присвоить имя Даты и т. д. 54

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов Третья часть шаблона (В 9: В 13) содержит формулы расчета значений показателей эффективности. Имея базовый шаблон, легко получить таблицу для любого числа периодов, вставив необходимое число строк в блок А 7: В 8 перед девятой строкой. При этом адреса ячеек в формулах будут корректно перенастроены, поскольку их абсолютная адресация обеспечена заранее заданием собственных имен. 55

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов Пример 6. Реализация проекта, предусматривающего затраты в размере 60000 ден. ед. должна дать чистый поток наличности, имеющий следующую структуру: 10000, 15000, 20000, 15000, 10000, 5000. Требуется определить: а) NPV, PI, IRR для проекта при норме дисконта 10% и 15%; б) NPV, PI, IRR при условии, что притоки денежной наличности одинаковы и составляют 13000 денежных единиц, а норма дисконта 12%; в) как изменятся NPV, PI, IRR, если последний приток наличности возрастет до 10000 денежных единиц; снизится до 2000 денежных единиц, а норма дисконта при этом составит 10%. 56

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов 57

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов 58

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов 59

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов 60

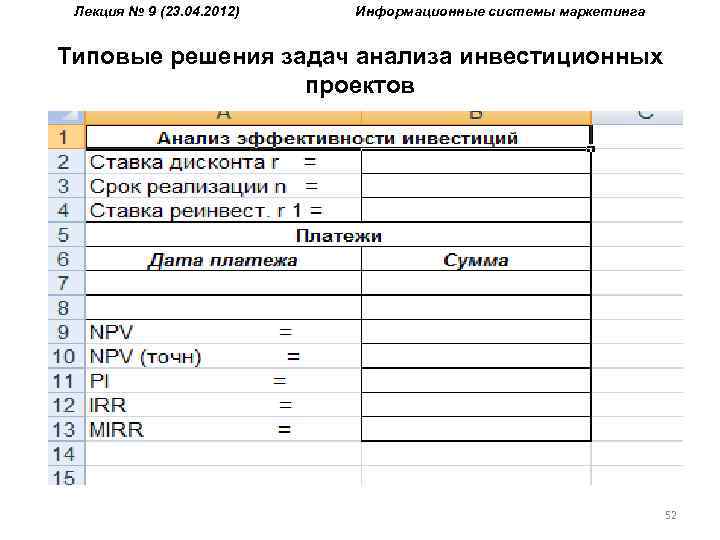
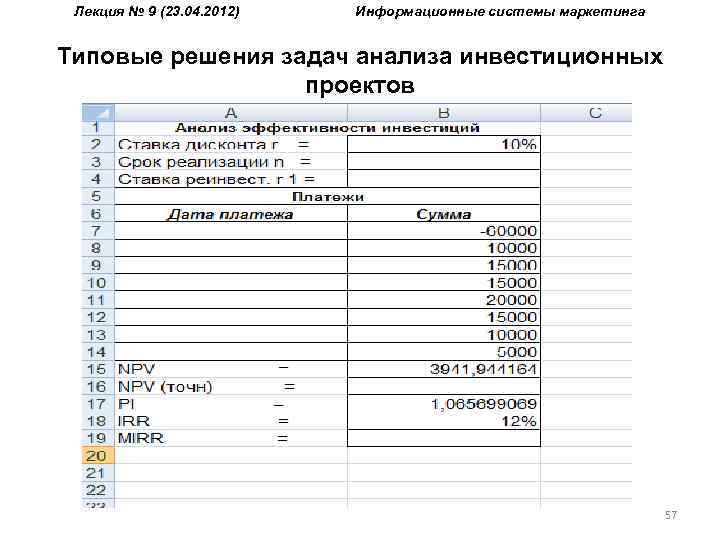
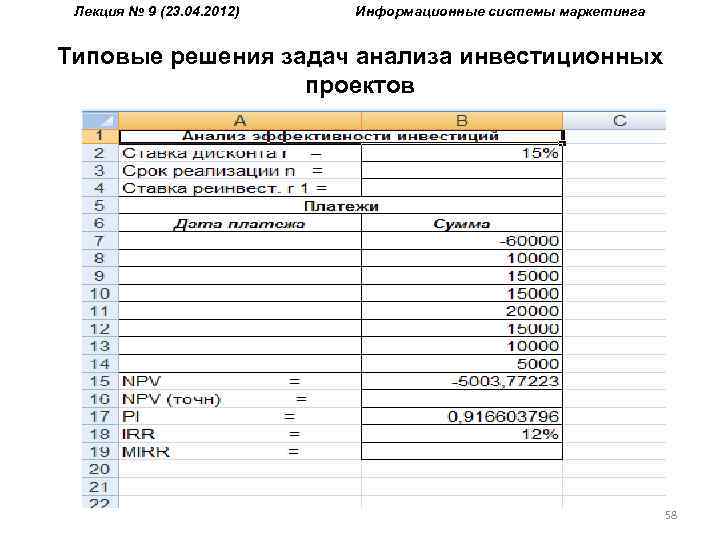
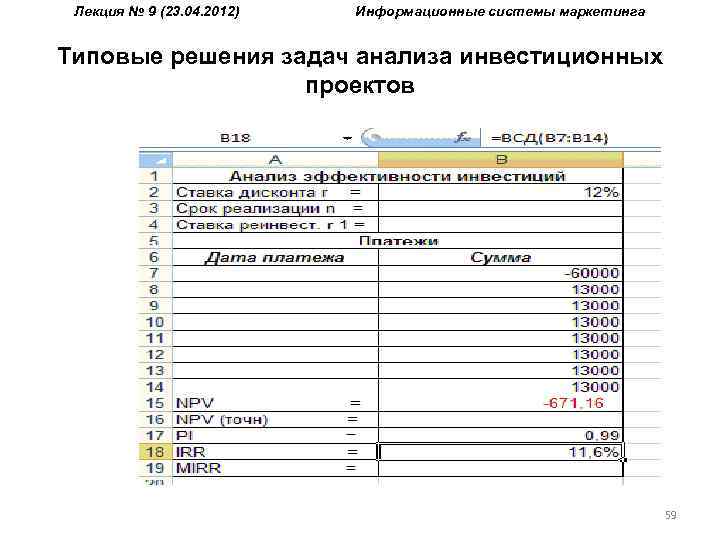
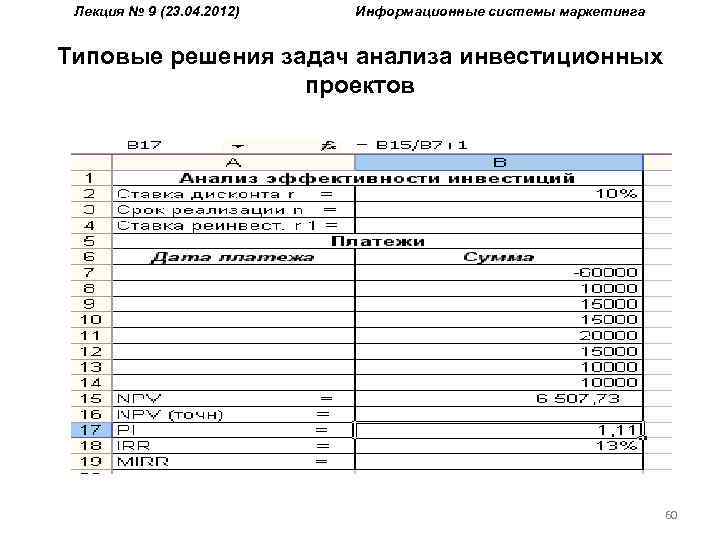
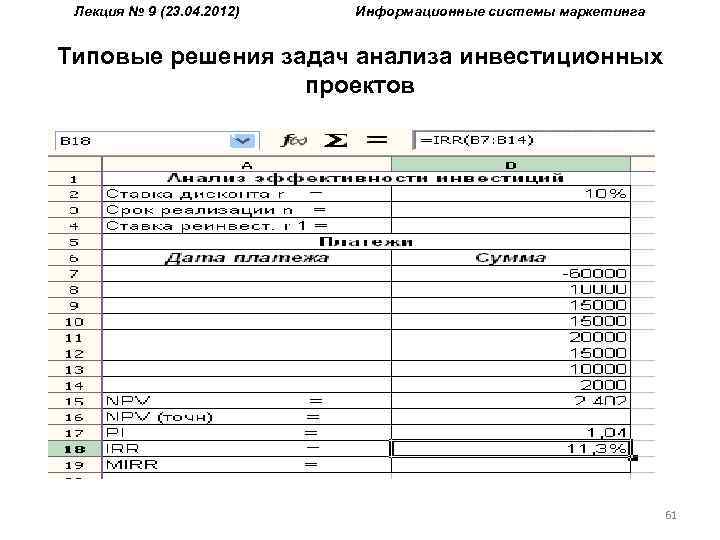
Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов 61

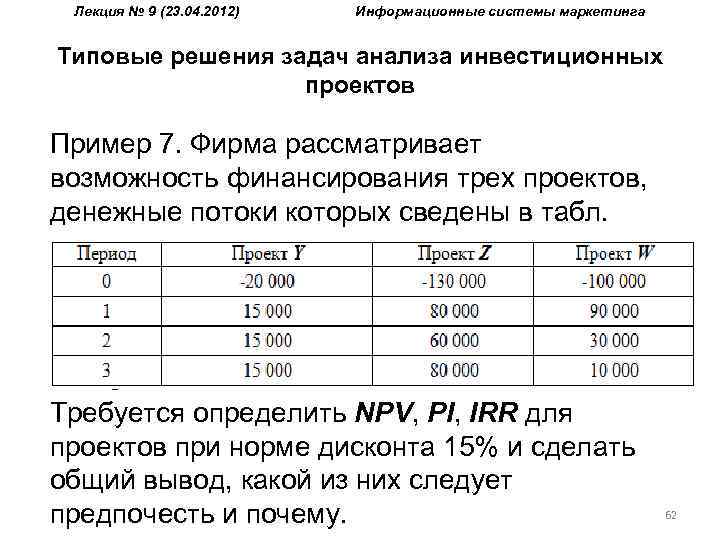Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов Пример 7. Фирма рассматривает возможность финансирования трех проектов, денежные потоки которых сведены в табл. Требуется определить NPV, PI, IRR для проектов при норме дисконта 15% и сделать общий вывод, какой из них следует предпочесть и почему. 62

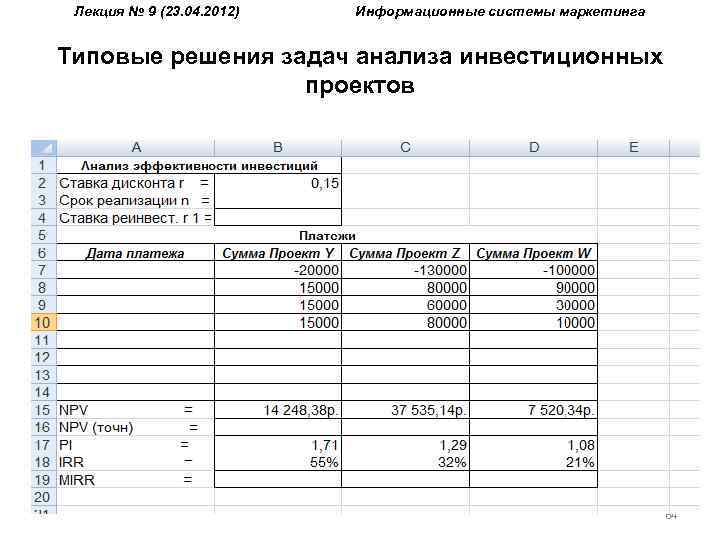
Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов Для примера 7 подготовленный шаблон необходимо видоизменить, применив известные методы работы в табличных процессорах. Обобщив все результаты, среди рассмотренных проектов следует выбрать проект Z, как обеспечивающий наибольшую чистую приведенную стоимость. 63

Лекция № 9 (23. 04. 2012) Информационные системы маркетинга Типовые решения задач анализа инвестиционных проектов 64