Лекция 9 1 Содержание предыдущей лекции Механические

Лекция 9 1

Содержание предыдущей лекции Механические колебания • • Разложение и синтез колебаний. Понятие о спектре колебаний. Связанные колебания. Волновое движение. Уравнение волны в газах, жидкостях и твердых телах. Плоская механическая волна. Длина волны, волновое число, фазовая скорость. Одномерное волновое уравнение. 2

Контрольный вопрос Скорость поперечной волны в упругой среде при увеличении амплитуды волны: а) возрастает, б) убывает, в) не меняется, г) нельзя однозначно ответить. в) 3

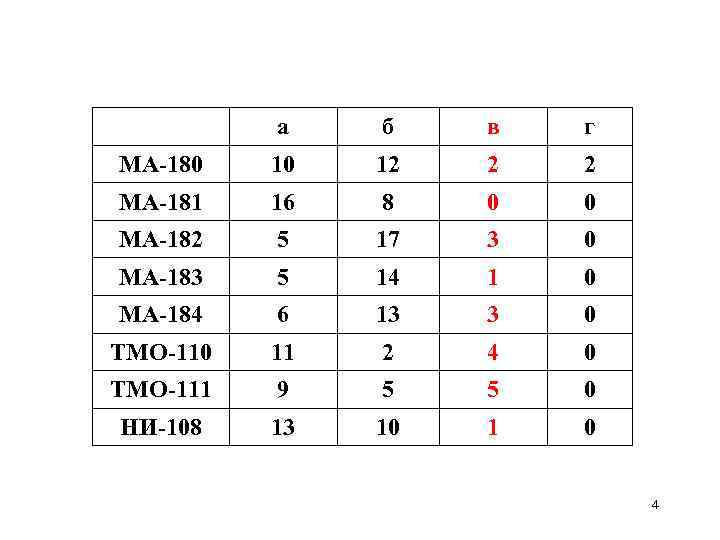а б в г МА-180 10 12 2 2 МА-181 16 8 0 0 МА-182 5 17 3 0 МА-183 5 14 1 0 МА-184 6 13 3 0 ТМО-110 11 2 4 0 ТМО-111 9 5 5 0 НИ-108 13 10 1 0 4

Содержание сегодняшней лекции Статистическая физика и термодинамика • Статистический и термодинамический методы. Термодинамические параметры. Равновесные и неравновесные состояния и процессы. Молекулярно-кинетическая теория (МКТ) • Макроскопическое состояние. Макроскопические параметры как средние значения микроскопических. Модель идеального газа. • Законы идеального газа. • Уравнение состояния идеального газа. • Давление газа с точки зрения МКТ. • Основное уравнение МКТ. • Среднеквадратичная скорость молекул. • Распределение Максвелла для молекул и проекций скорости молекул идеального газа, экспериментальное обоснование распределения Максвелла. 5

Статистическая физика и термодинамика Статистический и термодинамический способы описания процессов, происходящих в макроскопических телах, состоящих из большого количества атомов или молекул. 6

Статистическая физика - раздел физики, задача которого выразить свойства макроскопических тел, т. е. систем, состоящих из очень большого числа одинаковых частиц (молекул, атомов, электронов и т. д. ), через свойства этих частиц и взаимодействие между ними. Молекулярная физика – раздел физики, изучающий строение и свойства вещества на основе так называемых молекулярно-кинетических представлений. 7

Статистическая физика Молекулы (маленькие обособленные частицы) – составная часть любого тела (твердого, жидкого или газообразного). 8

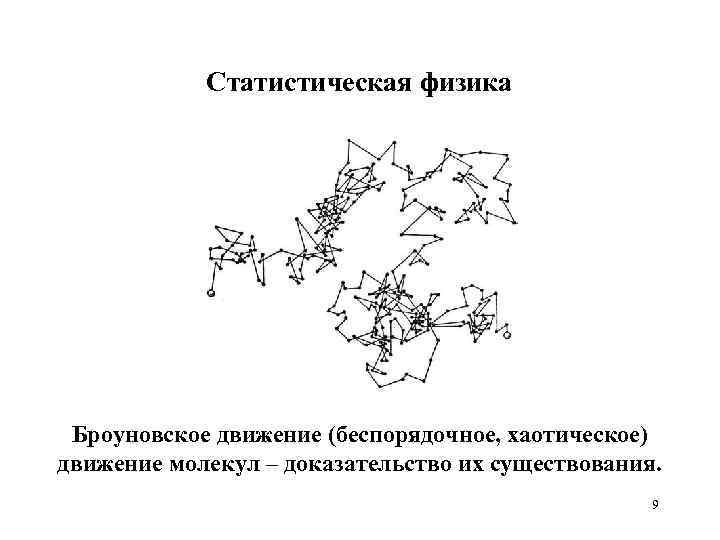Статистическая физика Броуновское движение (беспорядочное, хаотическое) движение молекул – доказательство их существования. 9

Статистическая физика Сложность наблюдения молекул – не столь устойчивые как атом структуры – разрушение при воздействии пучка электронов в просвечивающем электронном микроскопе. 10

Статистическая физика Ограничения статистического подхода: 1 см 3 газа (комнатная температура) – 3 · 1019 молекул. Около 1020 уравнений (по 3 на каждую молекулу) для описания движения молекул. Соотношение неопределенностей Гейзенберга – невозможность абсолютно точного одновременного определения координат и скоростей молекул. 11

Термодинамика – рассмотрение не отдельных молекул, а макроскопических тел, состоящих из огромного числа частиц. Термодинамика – описание тепловых явлений с помощью макроскопических величин (давление, температура, объем), которые не применимы к отдельным молекулам и атомам. Термодинамика - раздел физики, изучающий соотношения и превращения теплоты и других форм энергии. 12

Термодинамика Термодинамическая система – совокупность макроскопических тел, которые могут обмениваться энергией между собой и с внешней средой. 13

Модель идеального газа Допущения: • число молекул в газе велико, среднее расстояние между ними велико по сравнению с их размерами, • хаотичное движение молекул, соответствующее законам Ньютона, • взаимодействие молекул посредством упругих короткодействующих сил, • упругое взаимодействие молекул со стенками сосуда, • все молекулы газа одинаковы – простое вещество. 14

Модель идеального газа Соответствие модели поведению газа, состоящего из отдельных атомов при низких давлениях. Исключение из рассмотрения вращения и колебания молекул. 15

Уравнение состояния идеального газа Эксперимент: параметры состояния идеального газа связаны между собой b – постоянная, пропорциональная массе газа. 16

Уравнение состояния идеального газа 1 моль вещества – количество вещества, в котором содержится число частиц (атомов, молекул, ионов, электронов или других структурных единиц), равное числу атомов в 0, 012 кг изотопа углерода 12 С. Равенство числа частиц, содержащихся в 1 моле вещества, числу Авогадро NA = 6, 02213× 1023 моль-1. Закон Авогадро: 1 моль любого газа при нормальных условиях, т. е. при температуре 0 °С (273, 15 К) и давлении 1 атм (1, 013× 105 Па), занимает объем Vm = 22, 4 л. 17

Уравнение состояния идеального газа Относительная молекулярная масса вещества Mr – отношение массы молекулы этого вещества к 1/12 массы атома 12 С. Атомная единица массы mед – масса, равная 1/12 массы атома 12 С. Молярная масса (масса 1 моля) M = NAMrmед. 18

Уравнение состояния идеального газа Для 1 моля вещества: - молярная газовая постоянная или газовая постоянная. 19

Уравнение состояния идеального газа Для произвольного числа молей идеального газа 20

Давление газа с точки зрения МКТ Идеальный газ из N молекул в контейнере кубической формы с ребром d и объемом V. 21

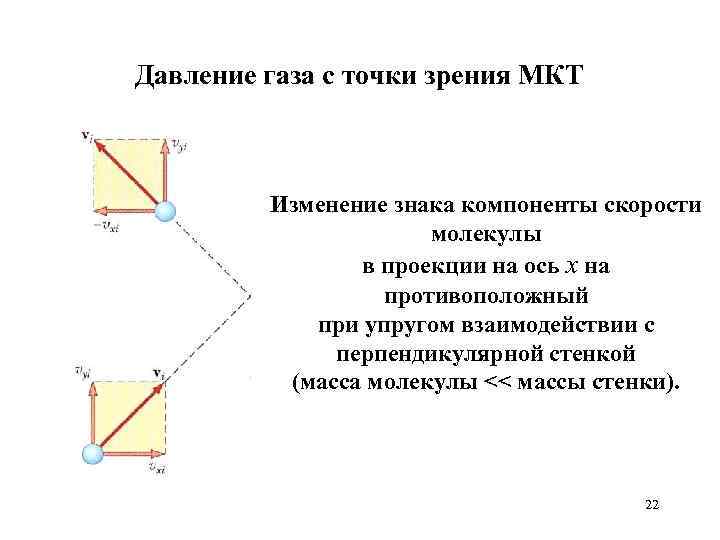Давление газа с точки зрения МКТ Изменение знака компоненты скорости молекулы в проекции на ось x на противоположный при упругом взаимодействии с перпендикулярной стенкой (масса молекулы << массы стенки). 22

Давление газа с точки зрения МКТ Модуль x - компоненты импульса молекулы: mvxi - до взаимодействия, mvxi - после взаимодействия. Изменение x - компоненты импульса молекулы в результате взаимодействия со стенкой Δpxi = mvxi (mvxi) = 2 mvxi. 23

Δpxi = mvxi (mvxi)= 2 mvxi Давление газа с точки зрения МКТ Второй закон Ньютона: - модуль x - компоненты усредненной силы, действующей на молекулу со стороны стенки за время ее взаимодействия со стенкой, - время взаимодействия молекулы со стенкой. 24

Давление газа с точки зрения МКТ Интервал времени между двумя последовательными соударениями молекулы с одной и той же стенкой 2 d - расстояние, пройденное молекулой между столкновениями внутри куба (перпендикулярно к стенке в направлении от нее и к ней). 25

Давление газа с точки зрения МКТ Второй закон Ньютона − модуль x - компоненты силы, действующей на молекулу со стороны стенки, усредненный по времени между двумя последовательными столкновениями молекулы со стенкой. 26

Давление газа с точки зрения МКТ Модуль x - компоненты средней силы, действующей на молекулу со стороны стенки, Третий закон Ньютона: усредненная x - компонента силы, действующей на стенку со стороны молекулы, 27

Давление газа с точки зрения МКТ Модуль средней силы, действующей на стенку, со стороны всех молекул газа, Большое количество молекул в газе – модуль средней силы, действующей на стенку, со стороны всех молекул газа, постоянен во времени. 28

Давление газа с точки зрения МКТ Cреднее значение квадрата скорости N молекул Сила, действующая на стенку со стороны всех молекул газа, 29

Давление газа с точки зрения МКТ Общий случай движения молекулы с проекциями компонентов вектора скорости vxi, vyi, vzi. Для молекул в целом: Движение молекул хаотичное: 30

Давление газа с точки зрения МКТ Сила, действующая на стенку, Давление, оказываемое на стенку молекулами газа, 31

Давление газа с точки зрения МКТ - ключевое соотношение, связывающее макро (давление) и микро (среднеквадратичная скорость молекул) параметры – макро и микромир. Давление газа прямо пропорционально числу молекул в единице объема и средней кинетической энергии их поступательного движения. 32

Давление газа с точки зрения МКТ - давление газа прямо пропорционально концентрации молекул и температуре. 33

Основное уравнение МКТ - основное уравнение МКТ, связывающее макроскопические (давление, объем, температура) и микроскопические (масса молекул, средняя скорость их движения) параметры термодинамической системы. 34

Cреднеквадратическая скорость молекул - мера средней кинетической энергии молекул. 35

Cреднеквадратическая скорость молекул Каждая поступательная степень свободы дает вклад, равный в энергию системы вдобавок к вкладу, связанному с перемещениями, вызванными с вращением и колебанием молекул. 36

Cреднеквадратическая скорость молекул Полная кинетическая энергия поступательного движения N молекул газа где k = R / NA – постоянная Больцмана, n = N / NA – число молей газа. Вывод: внутренняя энергия идеального газа зависит только от температуры. 37

Cреднеквадратическая скорость молекул M – молярная масса, равная m. NA. 38

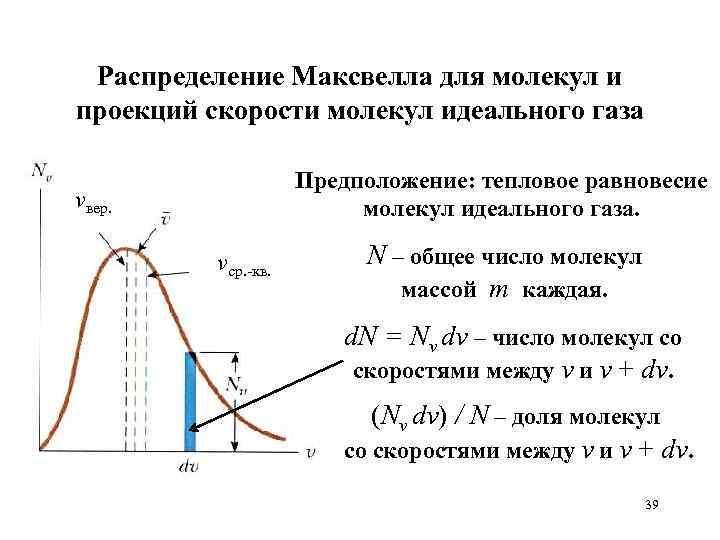Распределение Максвелла для молекул и проекций скорости молекул идеального газа Предположение: тепловое равновесие молекул идеального газа. vвер. vср. -кв. N – общее число молекул массой m каждая. d. N = Nv dv – число молекул со скоростями между v и v + dv. (Nv dv) / N – доля молекул со скоростями между v и v + dv. 39

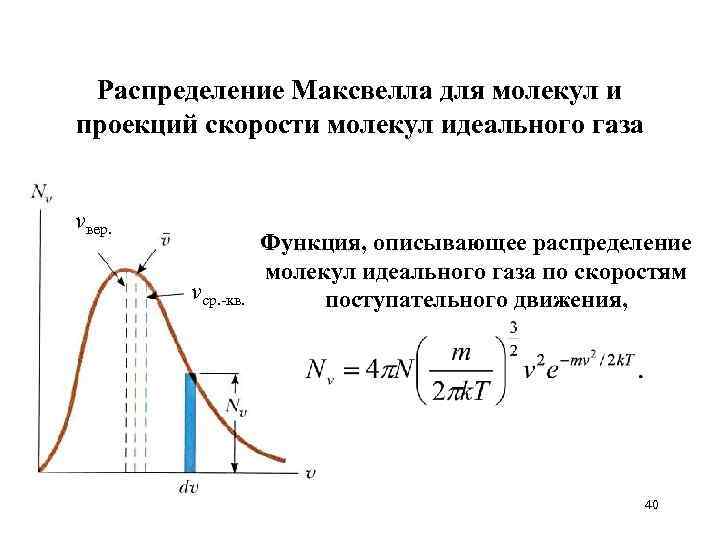Распределение Максвелла для молекул и проекций скорости молекул идеального газа vвер. vср. -кв. Функция, описывающее распределение молекул идеального газа по скоростям поступательного движения, 40

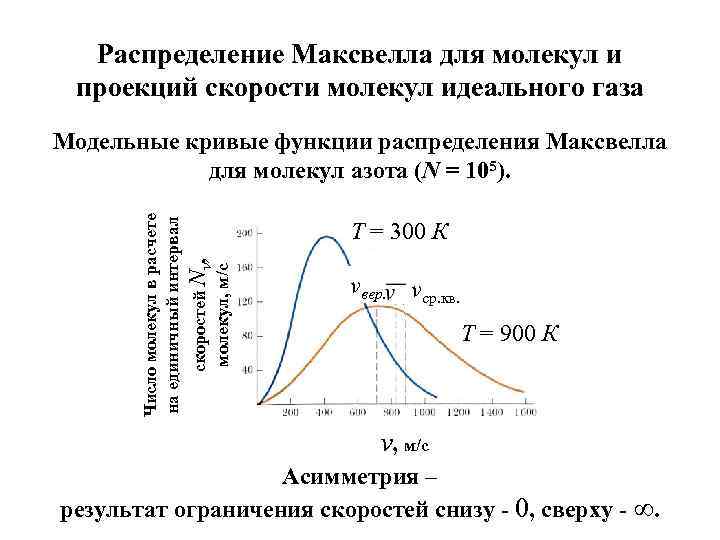Распределение Максвелла для молекул и проекций скорости молекул идеального газа Т = 300 К скоростей Nv, молекул, м/с Число молекул в расчете на единичный интервал Модельные кривые функции распределения Максвелла для молекул азота (N = 105). vвер. vcр. кв. Т = 900 К v, м/с Асимметрия – результат ограничения скоростей снизу - 0, сверху - ∞.

Распределение Максвелла для молекул и проекций скорости молекул идеального газа Сдвиг кривой вправо для менее массивных молекул – молекулы водорода и гелия легче покидают атмосферу Земли, чем более массивные молекулы азота и кислорода. Охлаждение воды при испарении – уход более энергетических молекул в воздух. 42

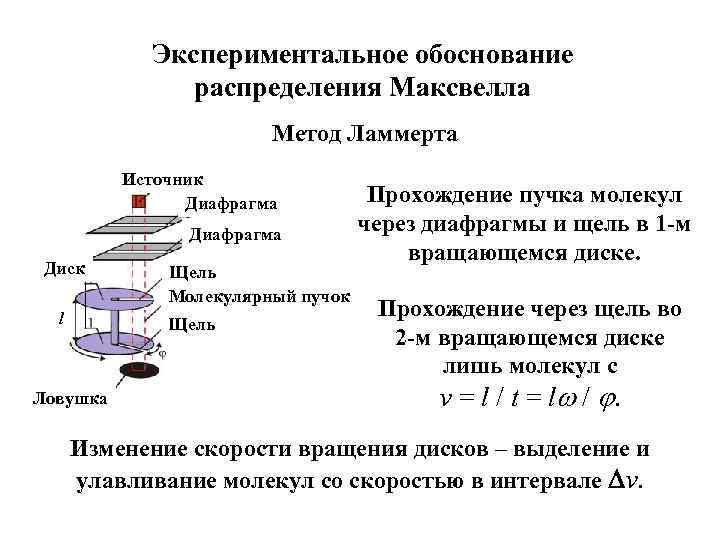Экспериментальное обоснование распределения Максвелла Метод Ламмерта Источник Диафрагма Диск l Щель Молекулярный пучок Щель Ловушка Прохождение пучка молекул через диафрагмы и щель в 1 -м вращающемся диске. Прохождение через щель во 2 -м вращающемся диске лишь молекул с v = l / t = l / . Изменение скорости вращения дисков – выделение и улавливание молекул со скоростью в интервале v.

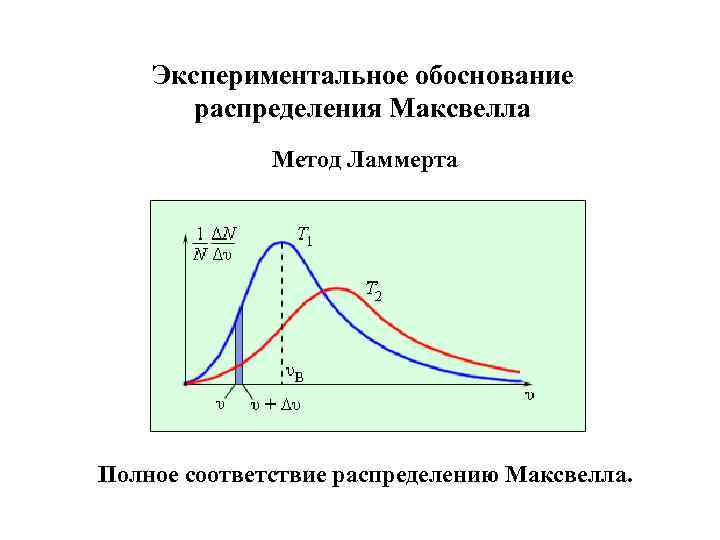Экспериментальное обоснование распределения Максвелла Метод Ламмерта Полное соответствие распределению Максвелла.

Контрольный вопрос В контейнерах А и Б содержится при одной и той же температуре один и тот же идеальный газ одинаковой массы. Объем контейнера Б в 2 раза больше, чем объем контейнера А. Средняя кинетическая энергия поступательного движения в расчете на 1 молекулу газа в контейнере Б по сравнению с таковой в контейнере А: а) больше в 2 раза, б) такая же, в) меньше в 2 раза, г) нельзя однозначно определить. 45