Лекция 8 ВЕКТОРНЫЙ АНАЛИЗ -ТЕОРИЯ ПОЛЯ Основные характеристики

Лекция 8 ВЕКТОРНЫЙ АНАЛИЗ -ТЕОРИЯ ПОЛЯ Основные характеристики скалярных полей I. Геометрические характеристики 2. Дифференциальные характеристики 3. Интегральные характеристики 4. Связь характеристик скалярного поля

Скалярное поле 1. Определение. Если с каждой точкой некоторой пространственной области связана скалярная величина, то в области задано скалярное поле( , , )P x y z G ( , , )u f x y z G — функция поля , , f x y z Примеры: поле температур, поле давления, поле плотности, поле концентраций, поле электрического заряда.

Геометрические характеристики скалярного поля — поверхности и линии уровня. Определение. Поверхностью уровня скалярного поля называется геометрическое место точек, удовлетворяющих уравнению)(Puu : ( )u P const Поверхность уровня эквипотенциальная поверхность

), ( yx. P), (yxuu. Линия уровня — геометрическая характеристика плоского поля constyxu. L), (: При помощи геометрических характеристик скалярные поля можно рисовать.

Пример 2. 2 2 2 e e e u r rx y z r — потенциал точечного заряда. : e const r : e c r , r const r — уравнение сферы 2 2 2 x y y const

Дифференциальные характеристики скалярного поля -2. характеристики отдельной точки поля. Рассмотрим скалярное поле где дифференцируемая функция. ( , , ), u u x y z ), , (zyxu 1. Производная по направлению — скалярная характеристика. Найдем, как изменяется поле в некотором направлении.

S S 1( , , )P x y z 2( , , )P x x y y z z SS 1 2 S P P r 222 zyx. SS Производной скалярного поля по направлению вектора в точке называется число Pu S P S u S 0 lim где ), , ( zyxuzzyyxxuu Определение.

Из определения следует : Смысл производной по направлению поле возрастает в точке в направлении . 0 S u u S P скорость изменения поля в точке в направлении . S u u S P поле убывает в точке в направлении . u S 0 S u P

Формула для вычисления u S Рассмотрим 2 1 ( )u u P ( , , )u x x y y z z u x y z ( ); u u u x y z 2 2 2 x y z S

Устремим 0 S 2 1 P P Рассмотрим *) ( )u u x u y u z S x S y S z S S 0 coscoscos

S x cos S z cos S y cos-направляющие косинусы коллинеарных векторов ( , , ) , S x y z S r r 0 cos , cos. S S S r r r. Координаты орта этих векторов: Таким образом, при правая часть равенства *) стремится к выражению 0 S SS z zu S y yu S x xu S u )( *) coscoscos zu yu xu

Следовательно, при существует предел левой части равенства *) , совпадающий с пределом правой части. 0 S cos cos P P PPu u S x y z Формула для вычисления производной по направлению

2. Градиент скалярного поля — векторная характеристика. , , u u u grad u u x y z r. Определение. Градиентом скалярного поля в точке называется вектор Pu. P Смысл характеристики — позже. Формула для вычисления – в определении характеристики.

Обозначим, , x y z r Формальный дифференциальный векторный оператор Гамильтона ( оператор “ набла ” ) , , u u x y z r , , u u u x y z Действие оператора “ набла ” на — результат формального умножения “ набла ” на . u u

Свойства оператора “ набла ” ; u v r r r 1. ; u u r r 2. ; uv v u u v r r r 3. ‘ ; f u u r r 4.

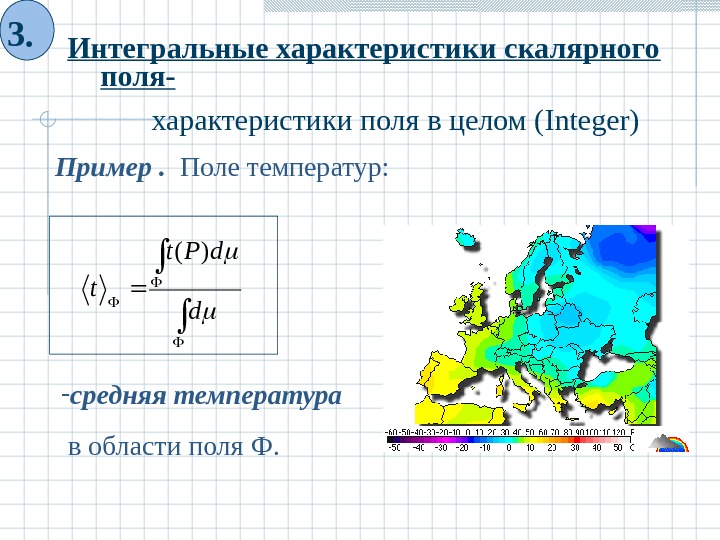
Интегральные характеристики скалярного поля-3. характеристики поля в целом ( Integer) Пример . Поле температур : d d. Pt t )( — средняя температура в области поля Ф.

Связь характеристик скалярного поля 4. 1. Градиент и производная по направлению. Другая запись формулы для вычисления S u coscoscos P PPP zu yu xu S u 0 P Pu u S S Ñ r r

2. Смысл градиента. Из формулы вычисления градиента следуетcos S P P u пр u u S r r r Если направление совпадает с направлением в точке Р , S u r то значение будет наибольшим ! P u S u r S

S P Pu пр u S Ñ r r а) — направлен в сторону наибыстрейшего возрастания поля u. u rб) max u u S Ñ r Длина градиента численно равна максимальной скорости возрастания скалярного поля u . S r uÑ r

3. Градиент и поверхности уровня. Рассмотрим : ( , , )u x y z c — уравнение поверхности уровня , , u u u gradu u x y z r u n r r- вектор нормали к касательной плоскости или к поверхности уровня Через точку проведем касательную плоскость: ( , , )P x y z 0 u u u x x y y z z x y z , , u u u n x y z r

Выводы. 1. Градиент направлен по нормали к поверхности уровня. 2. Направление нормали к поверхности уровня есть направление наибыстрейшего изменения скалярного поля. Понятие градиента может быть использовано для отыскания экстремума функции нескольких переменных численными методами.

Пример. 2 2 2 ; u x y z (1, 1, 1); P(1, 1, 1); S r ? P u S Решение. 0, P Pu u S S Ñ r r 2 , 2 u x y zÑ r 2, 2, 2 P uÑ r 0 (1, 1, 1) ; 3 S S S r r r 6 0 3 В точке Р в направлении поле возрастает с максимальной скоростью . S r

Основные характеристики скалярных полей I. Геометрические характеристики 2. Дифференциальные характеристики 3. Интегральные характеристики 4. Связь характеристик скалярного поля Линии, поверхности уровня Скалярная Векторная. P u S P uÑ r u