Лекція 8 Тема Криві лінії другого порядку на

Лекція 8 Тема. Криві лінії другого порядку на площині. Означення 1. Кривими лініями другого порядку називають лінії, координати точок яких задовольняють рівняння другого степеня відносно цих координат.

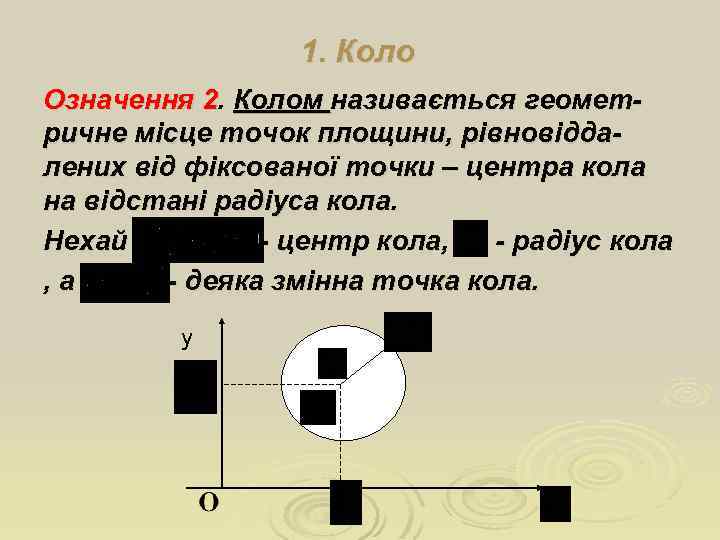1. Коло Означення 2. Колом називається геометричне місце точок площини, рівновіддалених від фіксованої точки – центра кола на відстані радіуса кола. Нехай - центр кола, - радіус кола , а - деяка змінна точка кола. у

За означенням кола , де , звідки випливає, що. Піднесемо до квадрата обидві сторони рівняння і одержимо рівняння кола: . Якщо в цьому рівнянні , то одержимо рівняння кола з центром у початку координат .

Обидва рівняння називають канонічними рівняннями кола. Якщо в рівнянні розкрити дужки, то одержимо загальне рівняння кола , де

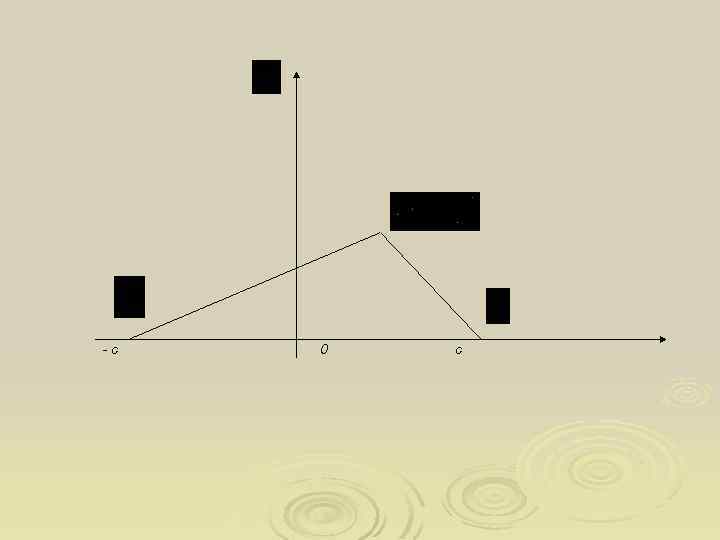
2. Еліпс Означення 3. Еліпсом називається геометричне місце точок площини, сума відстаней яких до двох заданих точок, які називають фокусами еліпса, є величиною сталою (позначимо її 2 а). Нехай - задані точки – фокуси еліпса. Вісь Ох проведемо через фокуси, а вісь Оу – через середину відрізка перпендикулярно до осі Ох.

-с 0 с

Нехай - довільна змінна точка еліпса, тоді за означенням еліпса маємо: . Перепишемо цю рівність в координатній формі і одержимо. Зробимо спрощення і виведемо позначення. - канонічне рівняння еліпса.

Дослідимо це рівняння. 1. Змінні х та у входять у рівняння еліпса у парних степенях, тому еліпс є фігурою симетричною відносно осей Ох та Оу. Точка О(0; 0) є центром симетрії еліпса і називається центром еліпса. 2. Знайдемо вершини еліпса як перетин його з осями координат: -з віссю Ох: ; -з віссю Оу: Отже, маємо дві вершини еліпса на осі Ох: і дві вершини на осі Оу: .

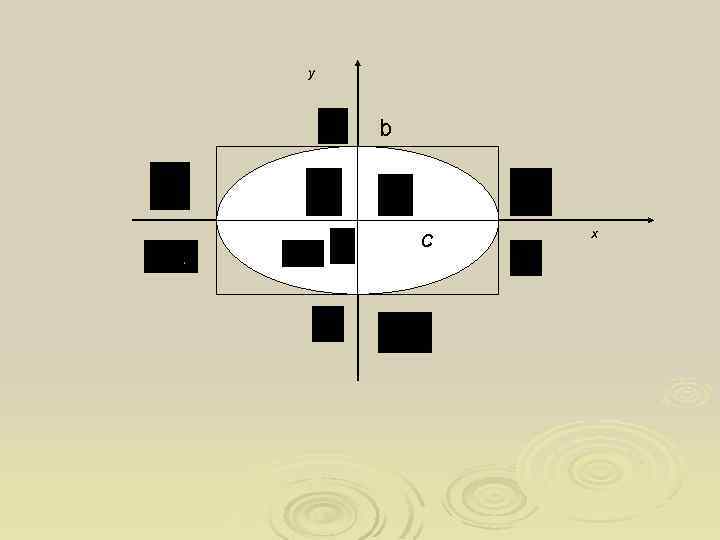
Відрізок називають великою віссю еліпса, відрізок а- великою піввіссю еліпса, відрізок - мала вісь еліпса, відрізок - мала піввісь еліпса. 3. Якщо в рівнянні еліпса , то одержимо рівняння кола: . Отже, коло – це частинний випадок еліпса. 4. Подальші дослідження рівняння еліпса показують, що еліпс має форму овала, який вписується у прямокутник зі сторонами і з центром у точці з двома взаємно перпендикулярними осями симетрії – осями координат.

y b c x

3. Гіпербола Означення 6. Гіперболою називається геометричне місце точок площини, модуль різниці відстаней яких до двох заданих точок, які називаються фокусами гіперболи, є величина стала. Нехай - фокуси гіперболи. Позначимо , тоді. Нехай - довільна точка гіперболи (рис. 5).

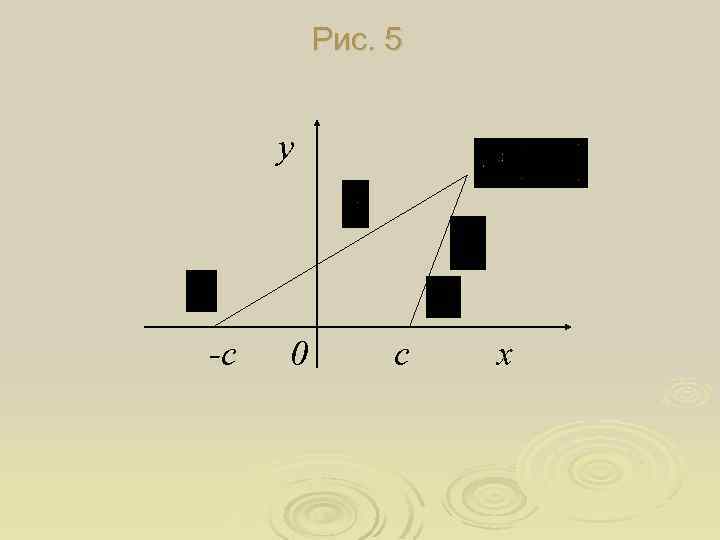Рис. 5 у -с 0 с х

і - фокальні радіуси точки гіперболи. З означення гіперболи випливає, що. Перепишемо останню рівність в координатній формі, враховуючи, що , . Маємо: .

Виконаємо перетворення, враховуючи той факт, що для гіперболи і можливе позначення , одержимо канонічне рівняння гіперболи: Знайдемо вершини гіперболи як точки перетину гіперболи з осями координат: Øз віссю Ох: ; Ø з віссю Оу: .

Дослідження рівняння гіперболи Ø гіпербола складається з двох нескінчених віток, які є симетричними відносно осей координат і початку координат; Ø будь-яка змінна точка гіперболи при її віддаленні у нескінченість необмежено наближається до однієї з двох прямих , які називають асимптотами гіперболи (рис. 6 );

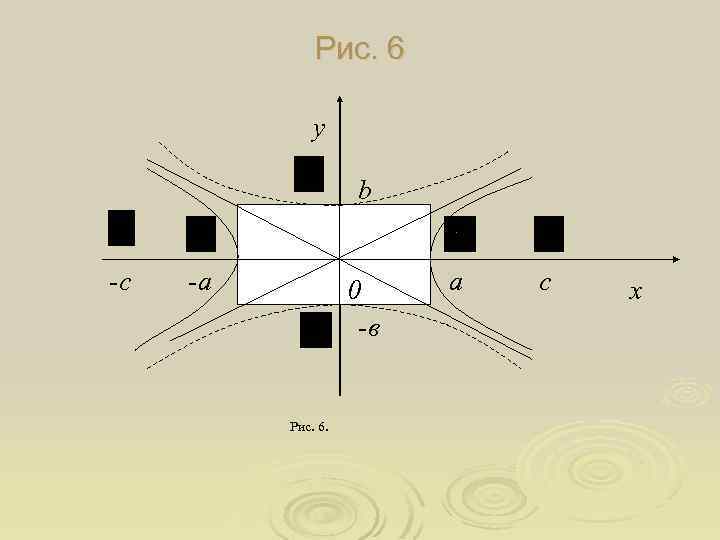Рис. 6 y b -c -а 0 -в Рис. 6. a c x

Øкожна гіпербола має так звану спряжену гіпер- болу, рівняння якої і яка має ті ж самі асимптоти і будується на тому ж самому малюнку, що і сама гіпербола (рис. 6). Графік спряженої гіперболи – пунктирна лінія.

Øфокуси гіперболи знаходяться на дійсній осі (яка лежить на осі Ох), зовні прямокутника зі сторонами , діагоналі якого є асимптотами гіперболи (фокуси спряженої гіперболи знаходяться на осі Оу); Øякщо , то така гіпербола називається рівнобічною; її рівняння має вигляд: ; асимптоти її є бісектрисами І і ІІІ та ІІ і ІV координатних кутів.

4. Парабола. Означення 8. Параболою називається геометричне місце точок площини, рівновіддалених від даної точки (фокуса параболи) і даної прямої (директриси параболи). Нехай - фокус параболи, - директриса параболи, а деяка змінна точка параболи (рис. 8). Тоді за означенням маємо рівняння параболи:

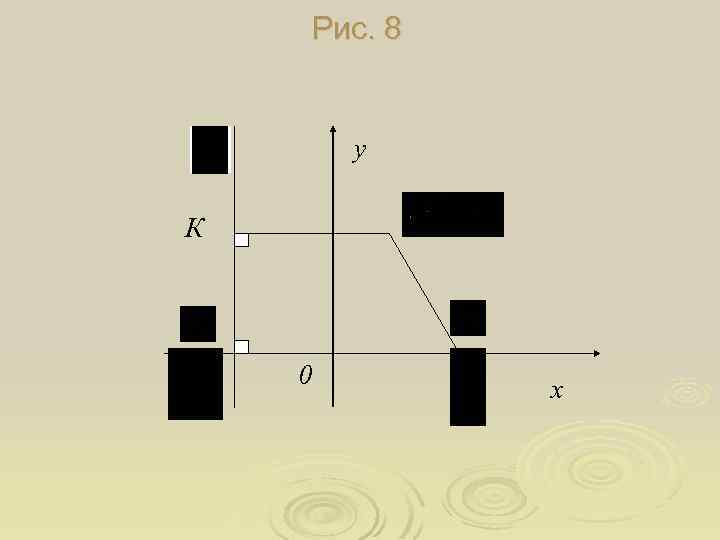Рис. 8 у К 0 х

Позначимо відстань між фіксованою точкою фіксованою прямою через вісь Ох пройде через точки через середину відрізка нього. Тоді ; і і . Нехай , а вісь Оу – перпендикулярно до , а рівняння директриси параболи має вигляд Перепишемо рівняння формі, враховуючи, що . в координатній

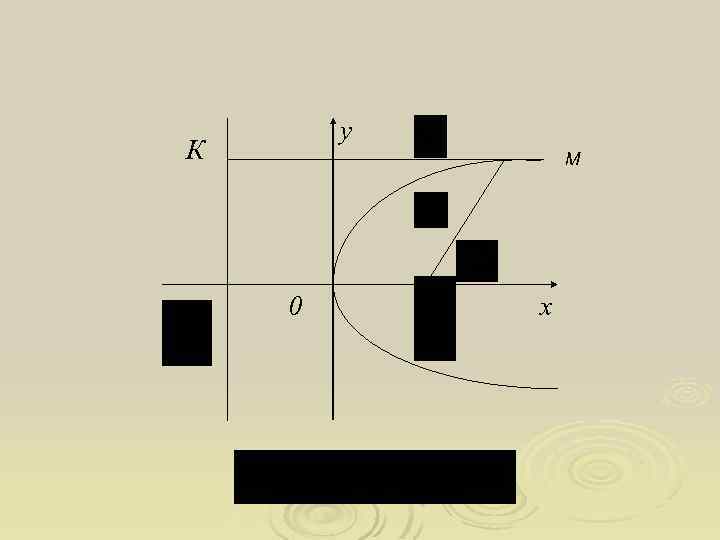
Маємо . Піднесемо обидві частини рівняння до квадрату і одержимо рівняння , яке називають канонічним рівнянням параболи. Це рівняння другого степеня. Дослідимо його. 1. Оскільки у рівнянні змінна у входить у парному степені, то парабола є фігурою, симетричною відносно осі Ох. 2. Якщо , то , і навпаки, тобто парабола перетинає вісі Ох, Оу в точці , яка називається вершиною параболи.

3. Оскільки , то звідси , тобто парабола розміщується справа від початку координат. 4. Із зростанням х зростає. Рівняння також є канонічними рівняннями параболи.

у К М 0 х

5. Дослідження рівняння другого порядку. Розглянемо загальне рівняння другого порядку, яке не містить добутку , а саме: . Якщо це рівняння є рівнянням деякої кривої другого порядку і, крім того, 1. , то це рівняння кола; 2. , тобто коефіцієнти А і В одного знаку, але різні за величиною, то це рівняння еліпса; 3. , тобто коефіцієнти А і В мають різні знаки, то це рівняння гіперболи; 4. ( або ), то це рівняння параболи.