Лекция 8 “ Конвективный теплообмен” Вопросы: 1. Конвективный

Лекция 8 “ Конвективный теплообмен” Вопросы: 1. Конвективный теплообмен Основные определения. 2. Использование основ теории подобия для расчета коэффициентов свободной и вынужденной конвекции. 3. Безразмерные комплексы для теплотехнических расчетов. 4. Теплоотдача при свободной и вынужденной конвекции.

Конвективным теплообменом (тепло-отдачей) называется процесс передачи тепла при омывании теплоносителем стенки. Процесс передачи тепла в этом случае осуществляется как за счет теплопроводности , так и конвекции. На процесс теплоотдачи влияют факторы: 1) природа возникновения движения жидкости вдоль стенки (свободное и вынужденное), свободное движение - естественная конвекция, обусловлена различием в плотности слоев жидкости из-за различия в температуре; вынужденное движение - перемещение жидкос-ти вентиляторами, насосами (движущая сила возникает за счет разности давлений ).

2) режим движения жидкости (лами- нарный и турбулентный). При ламинарном режиме средняя скорость в 2 раза меньше макси- мальной скорости движения потока вдоль стенки, при турбулентном - 1,2 -1,3 раза. Рейнольдс установил, что для течения жидко- сти в трубе при значениях комплекса Re = wd / менее 2300 - поток ламинарный , более 10000 - поток турбулентный, между ними – переходный режим. Здесь w- средняя скорость, d- диаметр трубы, - плотность жидкости, - ди- намическая вязкость жидкости. Длина участка стабилизации для ламинарного режима состав- ляет 0,03 d, для турбулентного - 40 d.

Режим движения жидкости определяет механизм переноса теплоты. При ламинарном режиме перенос осуще- ствляется за счет теплопроводности; при турбулентном - путем конвекции (лишь в приграничном ламинарном слое – теплопроводностью). Температура в тепловом пограничном слое при ламинарном режиме практичес- ки совпадает с характером распределения скоростей потока.

При турбулентном - температура распре- деляется полого лишь в пристенном лами- нарном слое, который имеет значительно меньшую толщину, чем в ламинарном. 3) Физические свойства жидкости ( , , , с, температуропроводность).  -динами- ческая вязкость характеризует силу тре- ния между соседними слоями на ед. повер- хности, =/  - кинематическая вязкость. 4) Форма, размеры, состояние поверх- ности стенки, омываемой жидкостью.

Для расчета теплового потока используют уравнение Ньютона Q=tS , q=t [7. 1] ; =/погр. слоя - коэффициент теплоотдачи (теплообмена, в строительной технике называется коэффициентом теплоперехода или тепловосприятия). t- температурный напор. Дифференциальное уравнение теплообмена описывает, согласно закона Фурье, процесс теплоотдачи на границах тела или [7.2] Для нахождения  необходимо знать температурный градиент, распределение температур в жидкости.

Для нахождения  необходимо знать температурный градиент, распределение температур в жидкости. Определение  и теплового потока на поверхности теплообмена является основной задачей теории конвективного теплообмена, которая решается с помощью основ теории подобия, её критериев. При решении данной задачи принимаются условия: тело омывается несжимаемой жидкостью, имеющую температуру и скорость вдали от тела постоянными и равными соответственно t0 и w0. Размер тела l0 задан и имеет постоянную величину для данного случая. Температура поверхности тела равна tc

Для определенности примем tc  t0. Полагаем, что физические параметры жидкости постоянны (учитываем только подъемную силу, возникающую в результате зависимости плотности от температуры ). Теплота трения не учитывается, процесс стационарный. Ось Оy нормальна к поверхности тела. Ось Ох направлена вдоль тела и вертикальна, при этом gx=g, а проекции вектора сил тяжести (или подъемной силы) на оси Ох и Оz равны нулю (gx=gz=0) Размер тела вдоль оси Oz намного больше l0

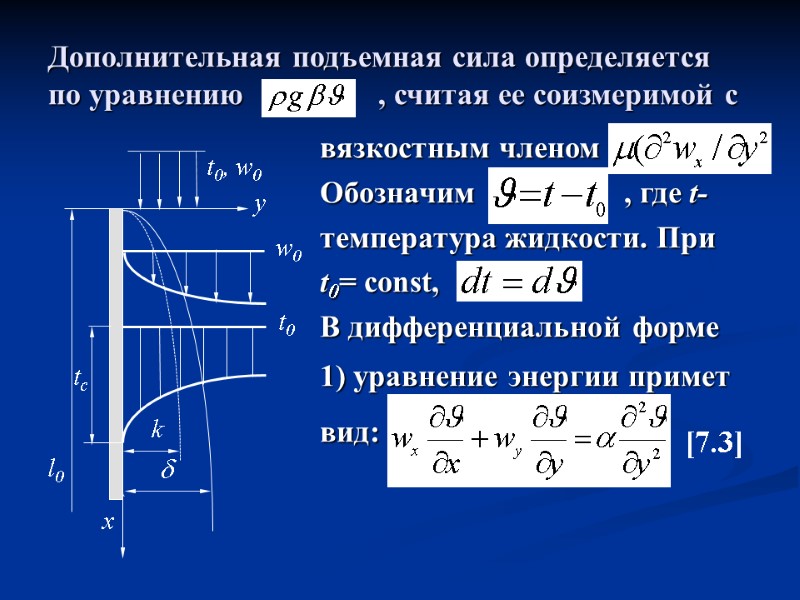
Дополнительная подъемная сила определяется по уравнению , считая ее соизмеримой с вязкостным членом Обозначим , где t- температура жидкости. При t0= const, В дифференциальной форме 1) уравнение энергии примет вид: [7.3]

2) уравнение движения: 3) уравнение сплошности потока: [7.5] [7.4] Здесь независимые переменные координаты х,у Зависимые переменные: , wx и wу Постоянные величины: w0 ; t0 ; l0 ;

Искомые переменные величины wх ; wу ; зависят от большого числа переменных и постоянных величин, входящих в условие однозначности. Все величины, входящие в перечисленные уравнения можно сгруппировать в комплексы, и количество безразмерных комплексов будет меньше числа размерных величин

Обозначим безразмерные величины: Для приведения к безразмерному виду выбирают масштаб: для линейных - длину поверхности теплообмена l0 , скорость w0, избы-точную температуру

Приведя выражение к безразмерному виду имеем: [7.8] ; ; ; ; Граничные условия в безразмерном виде будут выглядеть: 1) вдали от тела Wx=1, Wy=0 ; 2) на поверхности тела (Y=0, 0  X  1); ; Wx= Wy=0 ; При известном температур- ном поле коэффициент теплоотдачи определяется : [7.7]