ЛЕКЦИЯ 8 ИНТЕРФЕРЕНЦИЯ СВЕТА 8 1 Интерференция световых

ЛЕКЦИЯ 8. ИНТЕРФЕРЕНЦИЯ СВЕТА 8. 1 Интерференция световых волн от двух когерентных источников

Условия наблюдения интерференции Две гармонические световые волны называются когерентными, если они имеют одинаковую частоту и постоянную разность фаз колебаний световых векторов, возбуждаемыми этими волнами в какой-либо точке пространства. Интерференция – это явление перераспределения интенсивности света в пространстве в результате наложения когерентных волн. Условия, достаточные для наблюдения интерференции: когерентность световых волн; параллельность направлений колебаний световых векторов в волнах.

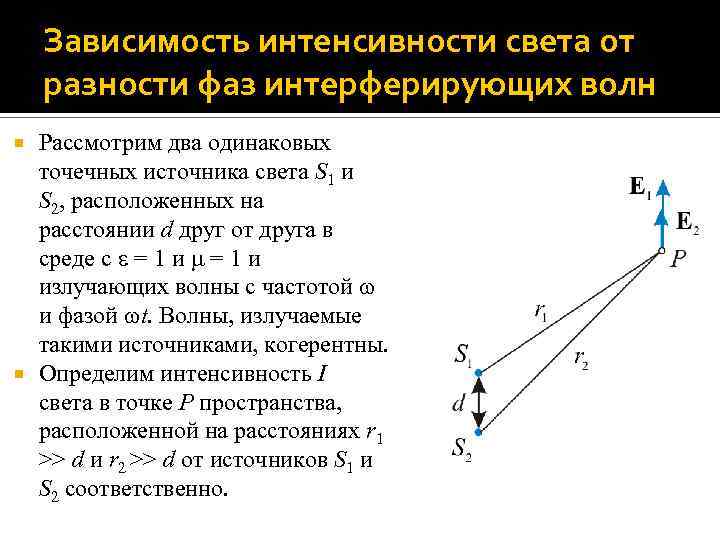Зависимость интенсивности света от разности фаз интерферирующих волн Рассмотрим два одинаковых точечных источника света S 1 и S 2, расположенных на расстоянии d друг от друга в среде с = 1 и излучающих волны с частотой и фазой t. Волны, излучаемые такими источниками, когерентны. Определим интенсивность I света в точке P пространства, расположенной на расстояниях r 1 >> d и r 2 >> d от источников S 1 и S 2 соответственно.

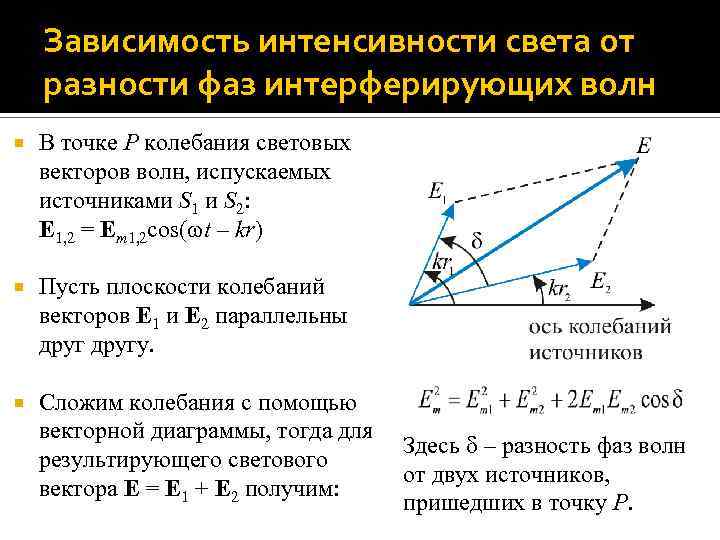Зависимость интенсивности света от разности фаз интерферирующих волн В точке P колебания световых векторов волн, испускаемых источниками S 1 и S 2: E 1, 2 = Em 1, 2 cos( t – kr) Пусть плоскости колебаний векторов E 1 и E 2 параллельны другу. Сложим колебания с помощью векторной диаграммы, тогда для Здесь – разность фаз волн результирующего светового от двух источников, вектора E = E 1 + E 2 получим: пришедших в точку P.

Зависимость интенсивности света от разности фаз интерферирующих волн Обозначим: – оптическая разность хода световых лучей, пришедших в точку P от источников. Тогда

Зависимость интенсивности света от разности фаз интерферирующих волн Интенсивности I 1 и I 2 света, пришедшего в точку P от каждого из источников, пропорциональны квадратам амплитуд Em 1 и Em 2 и соответственно равны: Здесь n – абсолютный показатель преломления среды, в которой распространяются волны. Тогда результирующая интенсивность света в точке P:

Зависимость интенсивности света от разности фаз интерферирующих волн Таким образом, зависимости интенсивности света от разности фаз складываемых волн дается выражением: Если интенсивности волн источников одинаковы (I 1 = I 2 = I 0), то

Зависимость интенсивности света от разности фаз интерферирующих волн Таким образом, интенсивность света в точке наблюдения зависит от разности фаз (разности хода ) когерентных волн, пришедших в точку P, и изменяется в пределах от 0 до 4 I 0. В результате наложения когерентных волн происходит перераспределение интенсивности света в пространстве: при переходе от одной точке к другой интенсивность света меняется (в случае наложения некогерентных волн интенсивность I была бы одинаковой и равной 2 I 0 в любой точке пространстве).

Условия максимума интерференции Для того, чтобы в точке P интенсивность света I была максимальной и равной 4 I 0 (при этом говорят, что в точке P наблюдается интерференционный максимум), должно выполняться условие: Тогда

Условия максимума интерференции Здесь число m называется порядком интерференционного максимума (или порядком интерференции). Это равенство означает, что оптическая разность хода лучей в точке максимума равна целому числу длин волн.

Найдем условия интерференционного минимума. Минимальное значение интенсивности света при наложении когерентных волн ( I = 0) имеет место, если Условия минимумаинтерференции Найдем условия интерференционного минимума Минимальное значение интенсивности света при наложении когерентных волн (I = 0) имеет место, если Тогда

Найдем условия интерференционного минимума. Минимальное значение интенсивности света при наложении когерентных волн ( I = 0) имеет место, если Условия минимума интерференции Таким образом, в точке, где наблюдается минимум интерференции, разность хода двух интерферирующих лучей равна полуцелому числу длин волн.

ЛЕКЦИЯ 5 ИНТЕРФЕРЕНЦИЯ СВЕТА 5. 2 Расчет интерференционной картины от двух щелей. Основные интерференционные схемы

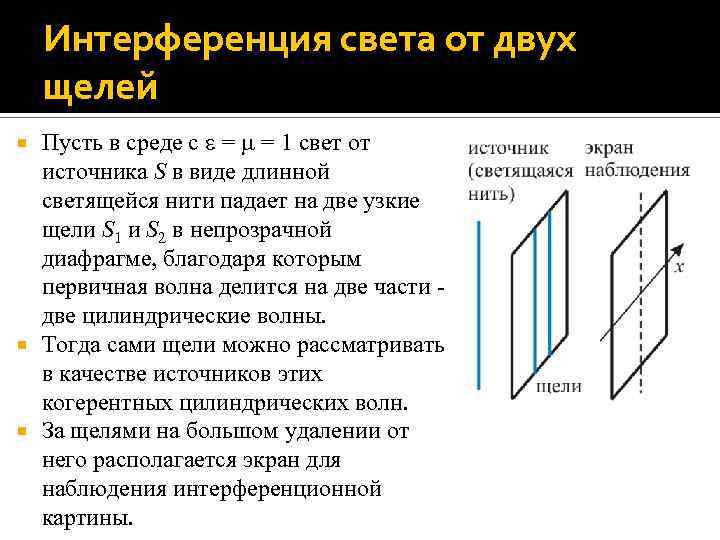Интерференция света от двух щелей Пусть в среде с = = 1 свет от источника S в виде длинной светящейся нити падает на две узкие щели S 1 и S 2 в непрозрачной диафрагме, благодаря которым первичная волна делится на две части - две цилиндрические волны. Тогда сами щели можно рассматривать в качестве источников этих когерентных цилиндрических волн. За щелями на большом удалении от него располагается экран для наблюдения интерференционной картины.

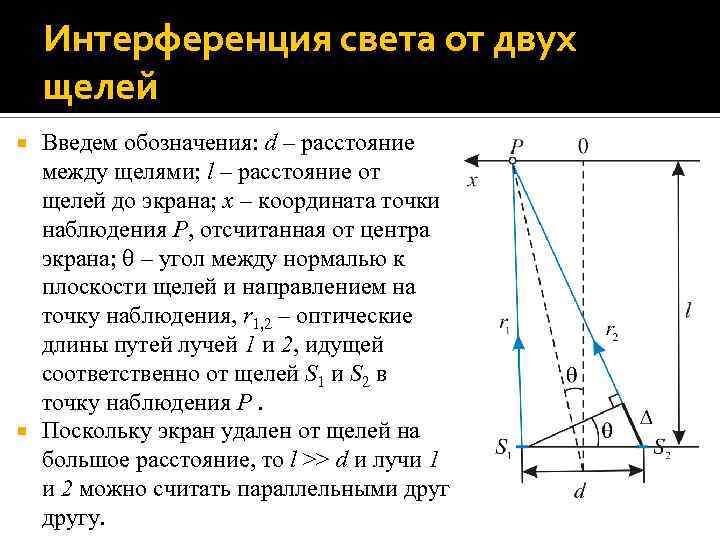Интерференция света от двух щелей Введем обозначения: d – расстояние между щелями; l – расстояние от щелей до экрана; x – координата точки наблюдения P, отсчитанная от центра экрана; – угол между нормалью к плоскости щелей и направлением на точку наблюдения, r 1, 2 – оптические длины путей лучей 1 и 2, идущей соответственно от щелей S 1 и S 2 в точку наблюдения P. Поскольку экран удален от щелей на большое расстояние, то l >> d и лучи 1 и 2 можно считать параллельными другу.

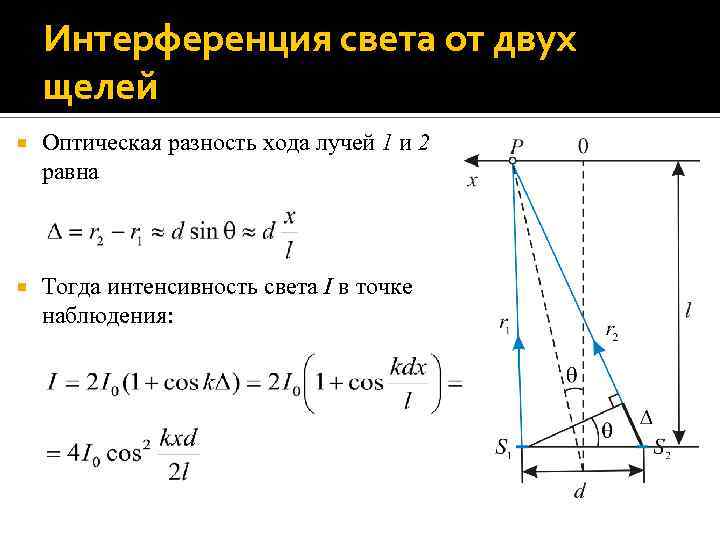Интерференция света от двух щелей Оптическая разность хода лучей 1 и 2 равна Тогда интенсивность света I в точке наблюдения:

Интерференция света от двух щелей Таким образом, наблюдается чередование светлых и темных полос, называемых интерференционными полосами. Светлые полосы соответствуют большей, темные – меньшей интенсивности света в интерференционной картине.

Ширина интерференционной полосы Шириной интерференционной полосы называется расстояние между двумя соседними максимумами (или минимума) интенсивности. Найдем положения на экране интерференционных максимумов. Из условия максимума интерференции имеем: Здесь m – порядок интерференции, или порядковый номер интерференционной полосы. Максимум 0 -го порядка (m = 0) и соответствующая интерференционная полоса располагаются на экране в центре интерференционной картины. С увеличением номера m соответствующая полоса смещается к периферии интерференционной картины.

Ширина интерференционной полосы Отсюда следует, что координата x m-й светлой полосы на экране: Ширина интерференционной полосы в этом случае равна:

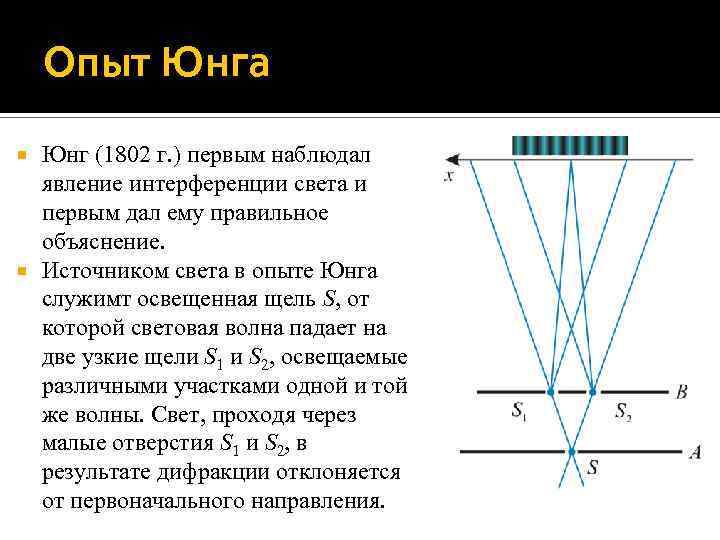Опыт Юнга Юнг (1802 г. ) первым наблюдал явление интерференции света и первым дал ему правильное объяснение. Источником света в опыте Юнга служимт освещенная щель S, от которой световая волна падает на две узкие щели S 1 и S 2, освещаемые различными участками одной и той же волны. Свет, проходя через малые отверстия S 1 и S 2, в результате дифракции отклоняется от первоначального направления.

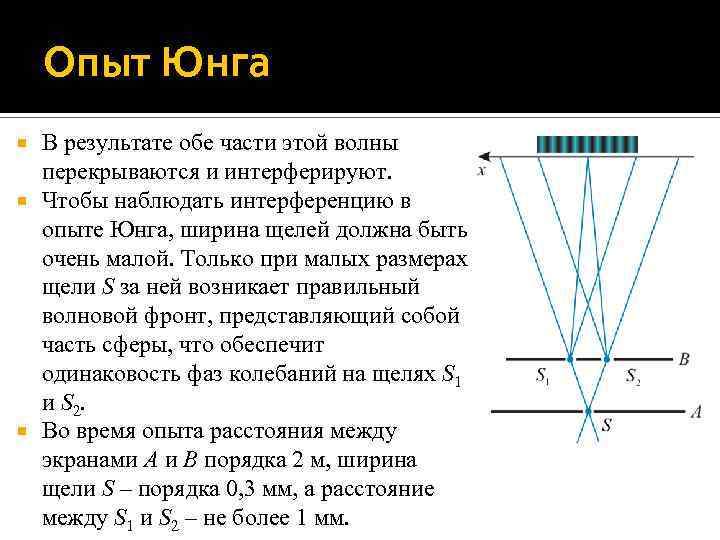Опыт Юнга В результате обе части этой волны перекрываются и интерферируют. Чтобы наблюдать интерференцию в опыте Юнга, ширина щелей должна быть очень малой. Только при малых размерах щели S за ней возникает правильный волновой фронт, представляющий собой часть сферы, что обеспечит одинаковость фаз колебаний на щелях S 1 и S 2. Во время опыта расстояния между экранами A и B порядка 2 м, ширина щели S – порядка 0, 3 мм, а расстояние между S 1 и S 2 – не более 1 мм.

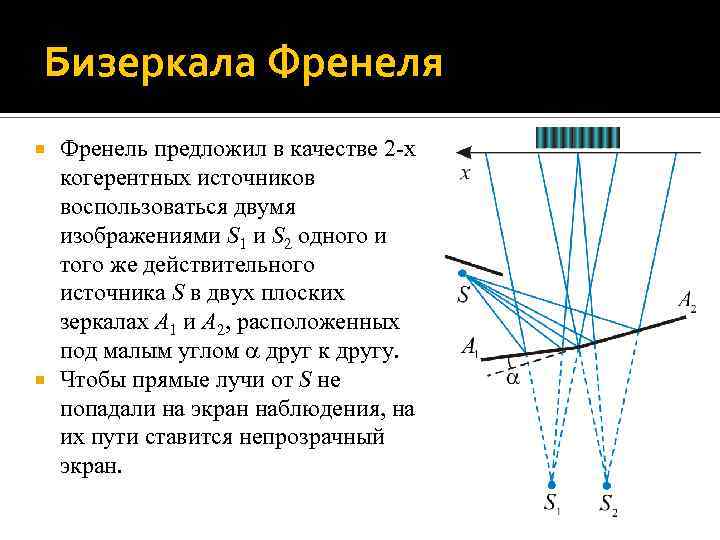Бизеркала Френеля Френель предложил в качестве 2 -х когерентных источников воспользоваться двумя изображениями S 1 и S 2 одного и того же действительного источника S в двух плоских зеркалах A 1 и A 2, расположенных под малым углом друг к другу. Чтобы прямые лучи от S не попадали на экран наблюдения, на их пути ставится непрозрачный экран.

Бизеркала Френеля Волны, идущие от S и отражающиеся зеркалами A 1 и A 2, представляют собой две системы когерентных волн, как бы исходящих от источников S 1 и S 2, являющихся мнимыми изображениями действительного источника S в зеркалах A 1 и A 2. Источник S в опыте Френеля берется в виде узкой щели, параллельной ребру, образованному зеркалами A 1 и A 2. При этом интерференционные максимумы имеют вид параллельных полос.

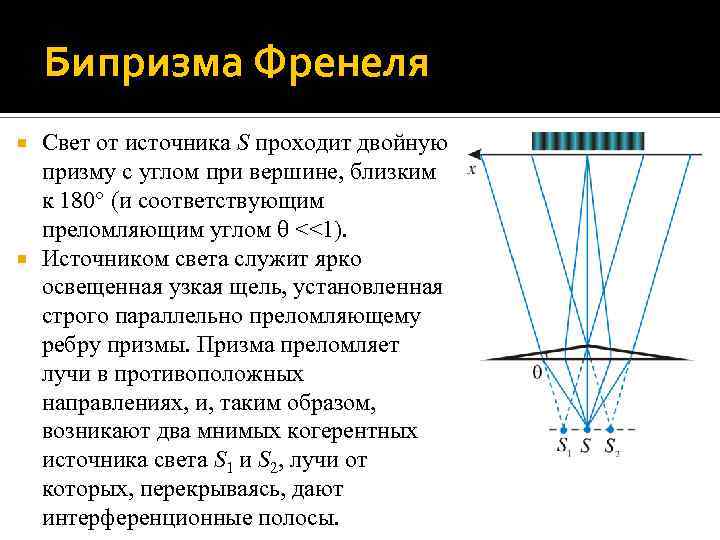Бипризма Френеля Свет от источника S проходит двойную призму с углом при вершине, близким к 180 (и соответствующим преломляющим углом <<1). Источником света служит ярко освещенная узкая щель, установленная строго параллельно преломляющему ребру призмы. Призма преломляет лучи в противоположных направлениях, и, таким образом, возникают два мнимых когерентных источника света S 1 и S 2, лучи от которых, перекрываясь, дают интерференционные полосы.

ЛЕКЦИЯ 8. ИНТЕРФЕРЕНЦИЯ СВЕТА 8. 2 Когерентность световых волн

Понятие когерентности. Критерий когерентности волн Две световые волны называются когерентными, если они характеризуются одинаковой частотой и постоянной в любой точке пространства разностью фаз. Расширим понятие когерентности не только на монохроматические волны, но и на естественный свет, представляющий собой суперпозицию гармонических волн с различными частотами, амплитудами и начальными фазами. Когерентностью называется согласованное протекание нескольких колебательных или волновых процессов. Критерий когерентности световых волн: две световые волны являются когерентными, если при их наложении возникает интерференционная картина (происходит пространственное перераспределение интенсивности света)

Понятие когерентности Пусть в некоторой точке пространства складываются волны, зависимость от времени световых векторов которых E 1 и E 2 описывается функциями: Эти функции можно считать гармоническими, но с изменяющимися во времени амплитудами E 1 m(t) и E 2 m(t) и начальными фазами 1(t) и 2(t). Обозначим: – характерное время, в течение которого параметры E 1 m, E 2 m, 1 и 2 успевают существенно измениться. Так, для монохроматического естественного света ~ 10 -8 с и намного порядков превышает период колебаний электромагнитного поля в световой волне: T ~ 10 -15 с.

Интенсивность света при интерференции Рассмотрим эти колебания в течение промежутка времени t, достаточно малого по сравнению с характерным временем . В течение этого промежутка времени E 1 m, E 2 m, 1 и 2 можно приближенно считать постоянными величинами, а сами колебания рассматривать как гармонические. Тогда интенсивность света в точке, в которой складываются две световые волны: Здесь = 2 – 1 const (в течение времени t) – разность фаз складываемых колебаний.

Мгновенная интенсивность В течение следующие промежутка времени t значения E 1 m, E 2 m, 1 и 2 вновь можно считать постоянными (но другими!). Тогда и интенсивность I света в точке сложения волн изменится. Таким образом, при наложении двух световых волн в какойлибо точке пространства интенсивность света зависит от времени: I = I(t) (мгновенная интенсивность света).

«Наблюдаемая» интенсивность света При наблюдении интерференции визуально (глазом) или с помощью какого-било оптического прибора регистрирует не мгновенное, а среднее по времени t значение интенсивности света: При этом усреднение осуществляется в течение времени срабатывания прибора или человеческого глаза, которое много больше введенного выше характерного времени . Сформулируем критерий когерентности световых волн.

Критерий когерентности световых волн Если две световые волны не когерентны, то при их наложении в пространстве интерференция не наблюдается, перераспределения интенсивности света не происходит, так что интенсивность в каждой точке равна сумме интенсивностей складываемых волн: Таким образом, в рассматриваемом случае

Критерий когерентности световых волн Если же две световые волны когерентны, то при их наложении в пространстве возникает интерференция; в каждой точке пространства интенсивность света Таким образом, в рассматриваемом случае

Критерий когерентности световых волн Таким образом, критерием когерентности световых волн (т. е. необходимым и достаточным условием когерентности) служит отличие от нуля среднего по времени значения рассчитываемого в каждой точке пространства, где имеет место наложение световых волн.

Характеристики естественного света Излучение светящегося тела слагается из волн, испускаемых многими атомами. Отдельные атомы излучают волновые цуги длительностью ~ 10 -8 с и пространственной протяженностью l ~ с 3 м (где c = 3 108 м/с – скорость света в вакууме). Каждый волновой цуг можно считать «обрывком» монохроматической волны ограниченной длительности и протяженности, которая характеризуется определенной частотой , амплитудой Em, начальной фазой и плоскостью колебаний светового вектора E. Эти параметры (за исключением ) никак не связаны с такими же параметрами предыдущего цуга. Таким образом, через время 10 -8 с излучение одной группы атомов хаотически сменяется излучением другой группы, из которых и складывается результирующая волна.

Характеристики естественного света Будем полагать, что испускаемая телом естественная световая волна – монохроматическая, т. е. у всех цугов = const. Естественный свет, как результат наложения отдельных «гармонических» цугов, является гармонической волной, однако ее амплитуда и начальная фаза претерпевают случайные изменения: Здесь E – проекция вектора E на определенное направление. Характерное время изменения амплитуды и начальной фазы имеет порядок средней длительности волнового цуга: ~ 10 -8 с.

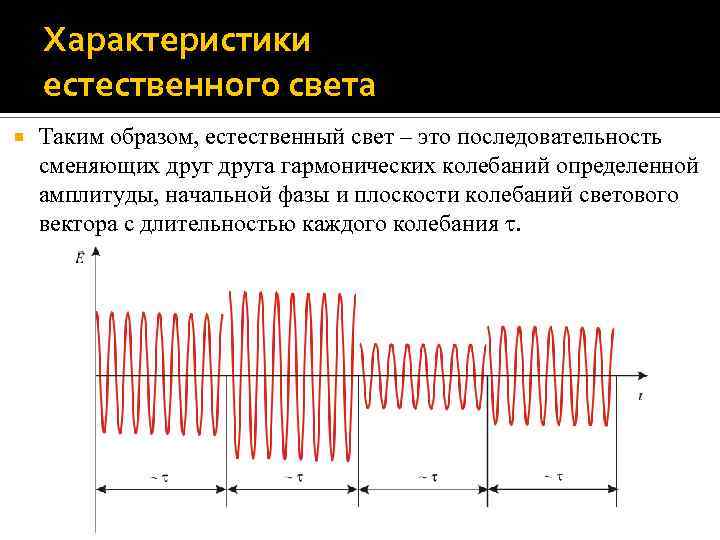Характеристики естественного света Таким образом, естественный свет – это последовательность сменяющих друга гармонических колебаний определенной амплитуды, начальной фазы и плоскости колебаний светового вектора с длительностью каждого колебания .

Время когерентности Временем когерентности с световой волны называется промежуток времени, в течение которого случайные изменения начальной фазы волны (t) достигают значения порядка . За это время волна «забывает» свою первоначальную фазу и становится некогерентной по отношению к самой себе. В рассматриваемой модели естественной световой волны время когерентности приблизительно равно длительности волнового цуга : Время когерентности c монохроматической естественной волны порядка 10 -8 с.

Длина когерентности Длиной когерентности lс световой волны называется расстояние, на которое распространяется волна за время, равное времени когерентности: Таким образом, длина когерентности приблизительно равно длине волнового цуга. Тогда для монохроматической естественной волны

Сложение естественных волн от двух независимых источников Рассмотрим два независимых источника естественного света S 1 и S 2, находящиеся в среде с = = 1, и точку наблюдения P, расстояния от которой до источников равны соответственно r 1 и r 2. Световые векторы в точке наблюдения: Разность фаз колебаний световых векторов в точке наблюдения P:

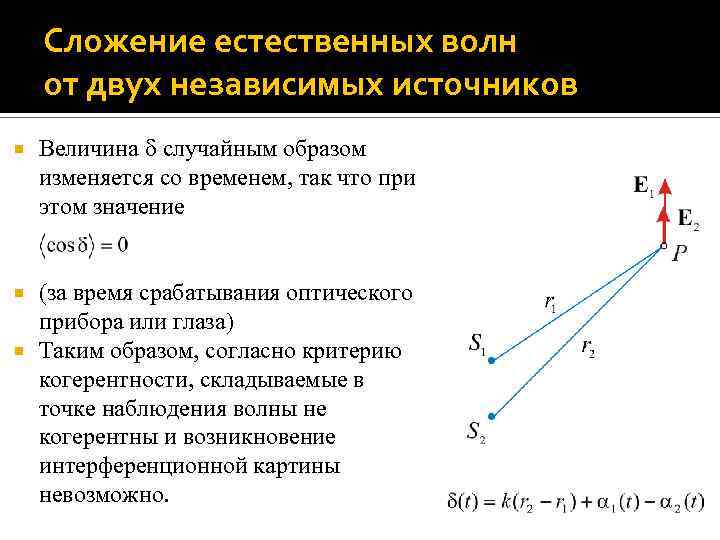Сложение естественных волн от двух независимых источников Величина случайным образом изменяется со временем, так что при этом значение (за время срабатывания оптического прибора или глаза) Таким образом, согласно критерию когерентности, складываемые в точке наблюдения волны не когерентны и возникновение интерференционной картины невозможно.

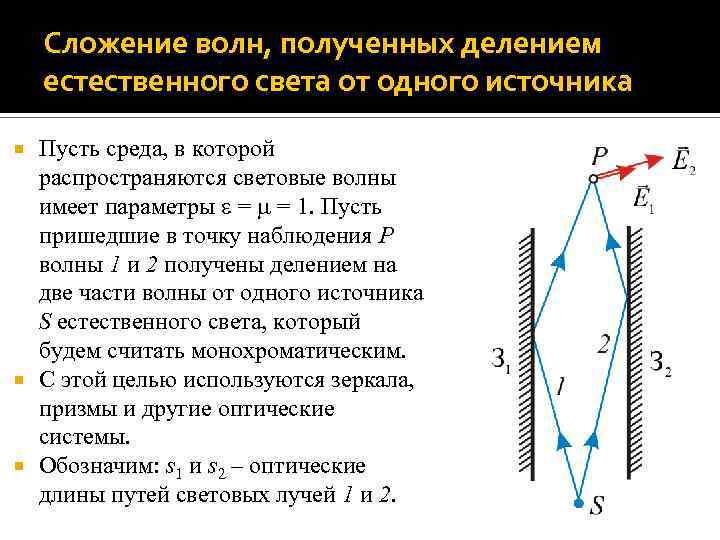Сложение волн, полученных делением естественного света от одного источника Пусть среда, в которой распространяются световые волны имеет параметры = = 1. Пусть пришедшие в точку наблюдения P волны 1 и 2 получены делением на две части волны от одного источника S естественного света, который будем считать монохроматическим. С этой целью используются зеркала, призмы и другие оптические системы. Обозначим: s 1 и s 2 – оптические длины путей световых лучей 1 и 2.

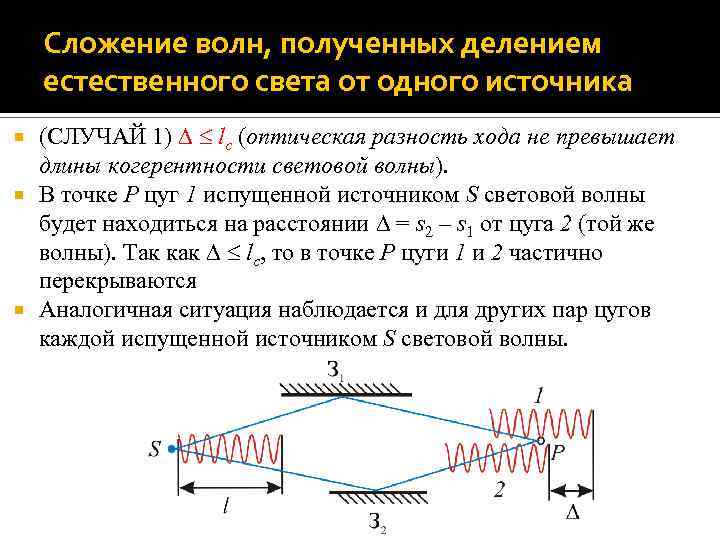Сложение волн, полученных делением естественного света от одного источника (СЛУЧАЙ 1) lc (оптическая разность хода не превышает длины когерентности световой волны). В точке P цуг 1 испущенной источником S световой волны будет находиться на расстоянии = s 2 – s 1 от цуга 2 (той же волны). Так как lc, то в точке P цуги 1 и 2 частично перекрываются Аналогичная ситуация наблюдается и для других пар цугов каждой испущенной источником S световой волны.

Сложение волн, полученных делением естественного света от одного источника Амплитуды и начальные фазы цугов 1 и 2 одинаковы (цуги – части одной и той же световой волны), поэтому световые волны результирующих волн в точке наблюдения: Таким образом, согласно критерию когерентности, наблюдение интерференции в естественном свете при наложении волн, полученных делением волны от одного источника, возможно, при условии того, что оптическая разность хода лучей не превышает длины когерентности естественной световой волны.

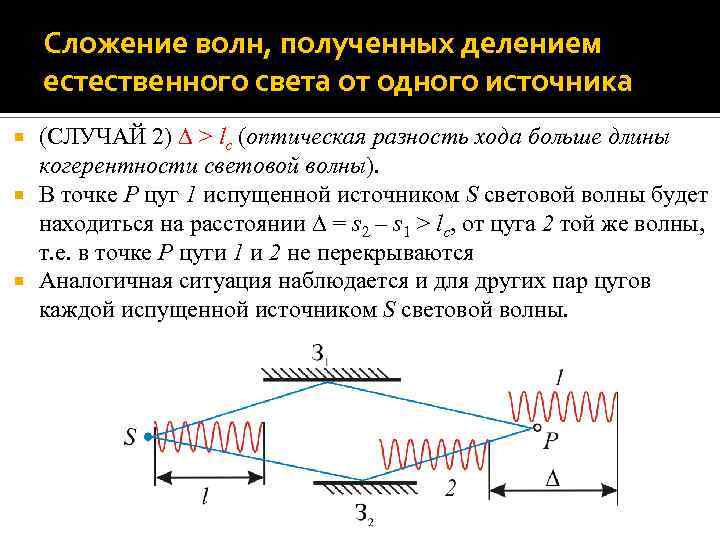Сложение волн, полученных делением естественного света от одного источника (СЛУЧАЙ 2) > lc (оптическая разность хода больше длины когерентности световой волны). В точке P цуг 1 испущенной источником S световой волны будет находиться на расстоянии = s 2 – s 1 > lc, от цуга 2 той же волны, т. е. в точке P цуги 1 и 2 не перекрываются Аналогичная ситуация наблюдается и для других пар цугов каждой испущенной источником S световой волны.

Сложение волн, полученных делением естественного света от одного источника Следовательно, амплитуды и начальные фазы цугов 1 и 2 различны (цуги, складывающиеся в точке P – это уже части различных световых волн), поэтому световые волны результирующих волн в точке наблюдения: Таким образом, согласно критерию когерентности, наблюдение интерференции в естественном свете при наложении волн, полученных делением волны от одного источника, невозможно в случае, если что оптическая разность хода лучей больше длины когерентности естественной световой волны.

ЛЕКЦИЯ 8. ИНТЕРФЕРЕНЦИЯ СВЕТА 8. 3 Интерференция в тонких пленках

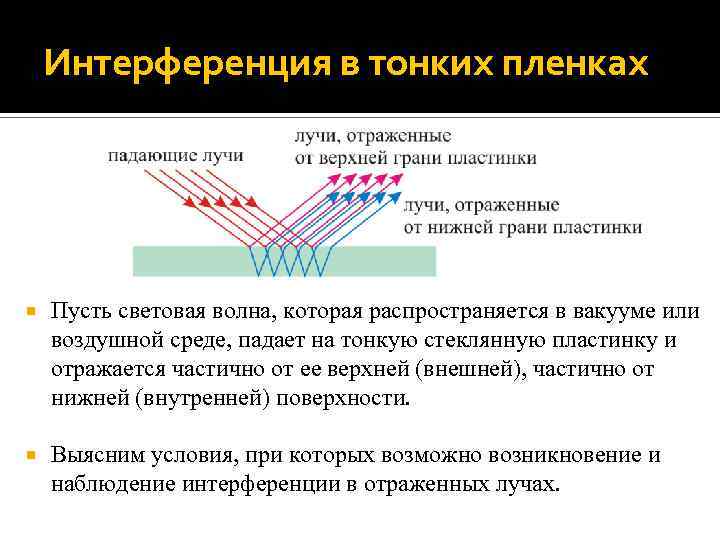Интерференция в тонких пленках Пусть световая волна, которая распространяется в вакууме или воздушной среде, падает на тонкую стеклянную пластинку и отражается частично от ее верхней (внешней), частично от нижней (внутренней) поверхности. Выясним условия, при которых возможно возникновение и наблюдение интерференции в отраженных лучах.

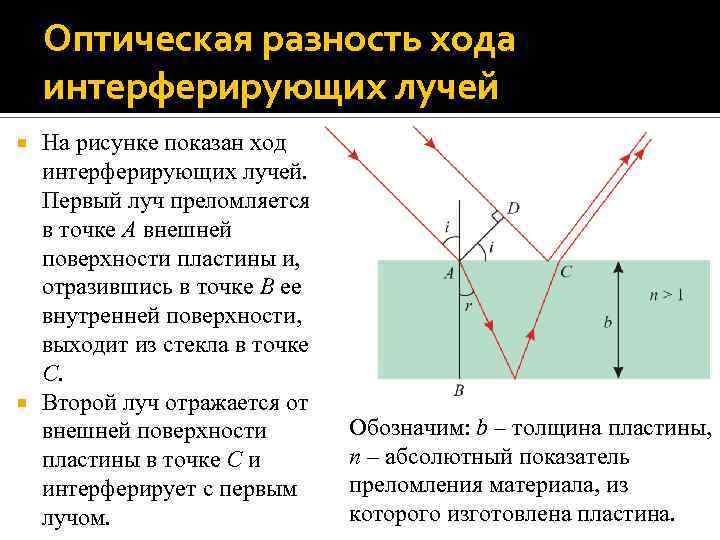Оптическая разность хода интерферирующих лучей На рисунке показан ход интерферирующих лучей. Первый луч преломляется в точке A внешней поверхности пластины и, отразившись в точке B ее внутренней поверхности, выходит из стекла в точке C. Второй луч отражается от внешней поверхности пластины в точке C и интерферирует с первым лучом. Обозначим: b – толщина пластины, n – абсолютный показатель преломления материала, из которого изготовлена пластина.

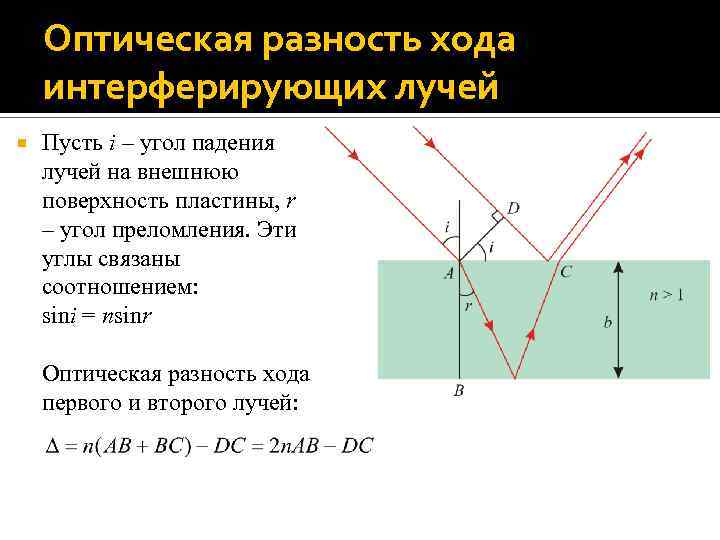Оптическая разность хода интерферирующих лучей Пусть i – угол падения лучей на внешнюю поверхность пластины, r – угол преломления. Эти углы связаны соотношением: sini = nsinr Оптическая разность хода первого и второго лучей:

Оптическая разность хода интерферирующих лучей Преобразуем выражение: При отражении от поверхности стекла световой волны, падающей на эту поверхность из воздуха (вакуума), фаза волны скачком изменяется на , что соответствует дополнительному оптическому пути /2.

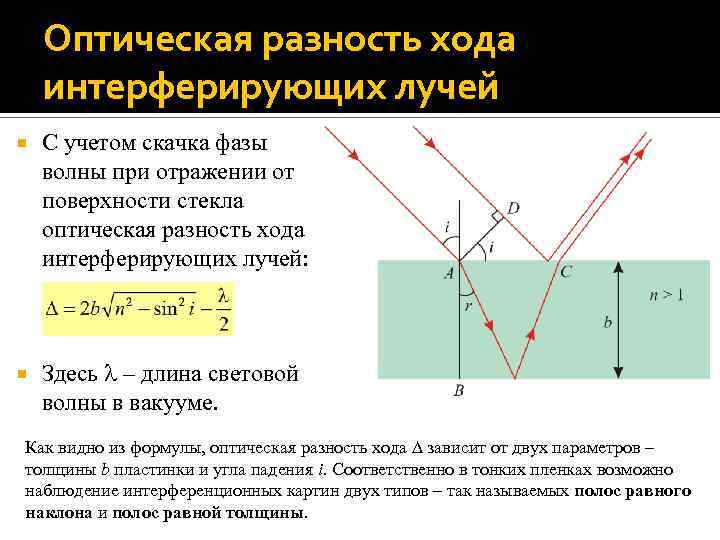Оптическая разность хода интерферирующих лучей С учетом скачка фазы волны при отражении от поверхности стекла оптическая разность хода интерферирующих лучей: Здесь – длина световой волны в вакууме. Как видно из формулы, оптическая разность хода зависит от двух параметров – толщины b пластинки и угла падения i. Соответственно в тонких пленках возможно наблюдение интерференционных картин двух типов – так называемых полос равного наклона и полос равной толщины.

Полосы равного наклона возникают и наблюдаются при выполнении следующих условий: тонкая прозрачная пластинка или пленка является плоскопараллельной, т. е. имеет постоянную толщину b = const; пластинка освещается рассеянным светом: световые лучи падают на поверхность пластинки под разными углами, 0 i /2; Интерференционная картина наблюдается либо на экране в фокальной плоскости линзы, расположенной вблизи пластинки, либо (в отсутствие линзы) непосредственно глазом, смотрящим на пластинку и аккомодированным на бесконечность (в этом случае хрусталик глаза играет роль линзы, а сетчатка – роль экрана).

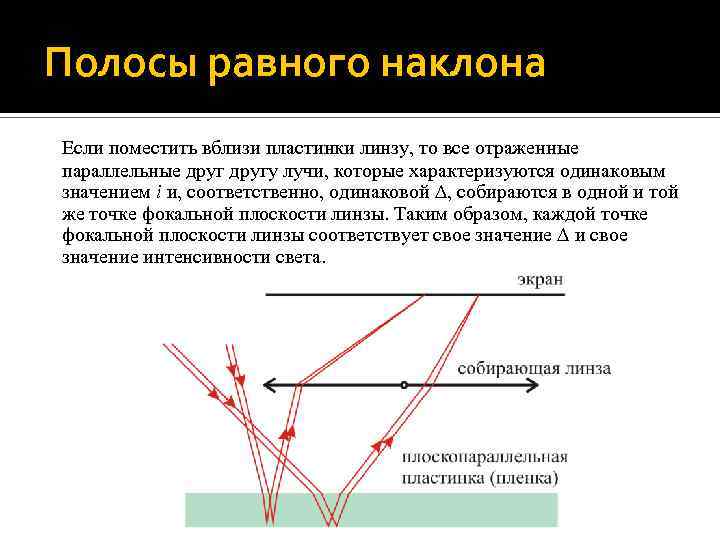Полосы равного наклона Если поместить вблизи пластинки линзу, то все отраженные параллельные другу лучи, которые характеризуются одинаковым значением i и, соответственно, одинаковой , собираются в одной и той же точке фокальной плоскости линзы. Таким образом, каждой точке фокальной плоскости линзы соответствует свое значение и свое значение интенсивности света.

Полосы равной толщины возникают и наблюдаются при выполнении следующих условий: Толщины пластинки b меняется от точки к точке (например, стеклянная пластинки имеет форму клина; в качестве пластинки можно взять линзу и т. д. ); Пластинка освещается параллельным пучком света, так что углы падения всех лучей одинаковы: i = const. Интерференционные полосы наблюдаются непосредственно на поверхности пластинки или вблизи этой поверхности (в окружающем пластинку пространстве)

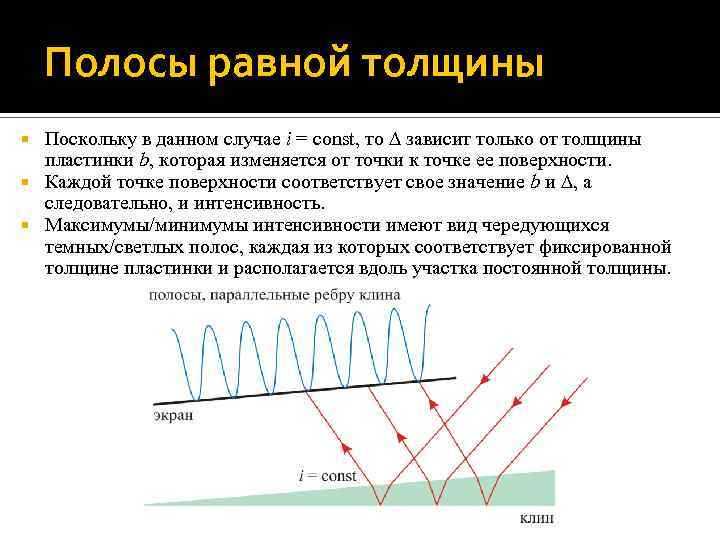Полосы равной толщины Поскольку в данном случае i = const, то зависит только от толщины пластинки b, которая изменяется от точки к точке ее поверхности. Каждой точке поверхности соответствует свое значение b и , а следовательно, и интенсивность. Максимумы/минимумы интенсивности имеют вид чередующихся темных/светлых полос, каждая из которых соответствует фиксированной толщине пластинки и располагается вдоль участка постоянной толщины.

Полосы равной толщины По порядку величины во всех интерференционных опытах с тонкими пленками оптическая разн 6 ость хода равна: Как известно, для того чтобы интерференция была возможна, необходимо, чтобы Здесь lc – длина когерентности. Если, например, длина световой волны = 550 нм, а ширина спектрального интервала = 2 нм, то lc ~ 0, 1 мм, следовательно для стекла (n = 1, 5) толщина пленки не должна превышать b ~ 0, 03 м.

Полосы равной толщины Примерами из повседневной жизни, в которых наблюдается интерференция в тонких пластинках (пленках), служат окрашенные полосы на поверхности нефтяных и масляных пятен и мыльных пузырей, а также цвета на поверхности закаленного металла.

Кольца Ньютона Классическим примером полос равной толщины являются кольца Ньютона, образующиеся в зазоре между сферической линзой и плоскопараллельной пластинкой. Их лучше наблюдать в отраженном свете. В этом случае в центре картины за счет фазового скачка при отражении образуется темное пятно.

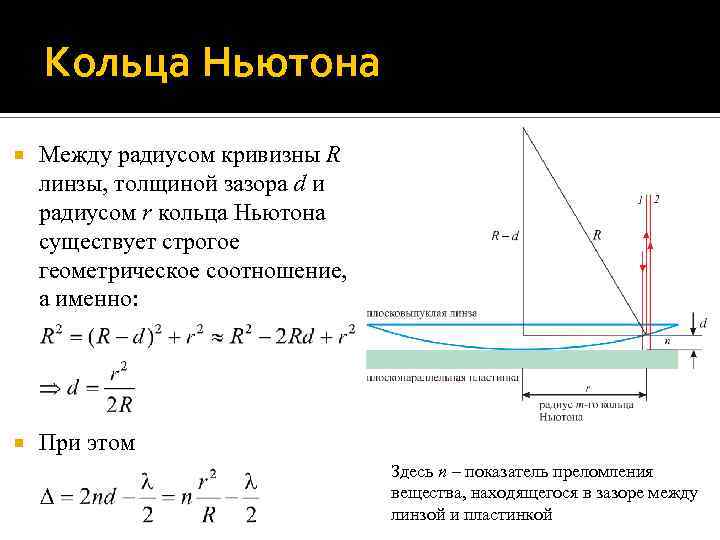Кольца Ньютона Между радиусом кривизны R линзы, толщиной зазора d и радиусом r кольца Ньютона существует строгое геометрическое соотношение, а именно: При этом Здесь n – показатель преломления вещества, находящегося в зазоре между линзой и пластинкой

Кольца Ньютона С учетом условия максимума интерференции ( = m ), радиусы светлых колец Ньютона в отраженном свете: При выполнении условия минимума интерференции ( = (m + 1/2) ) получим формулу для расчета радиусов темных колец Ньютона в отраженном свете: