
Лекция 8 1). II 2). а). Различные способы определения м. ц. с. II ; и направлены в разные стороны
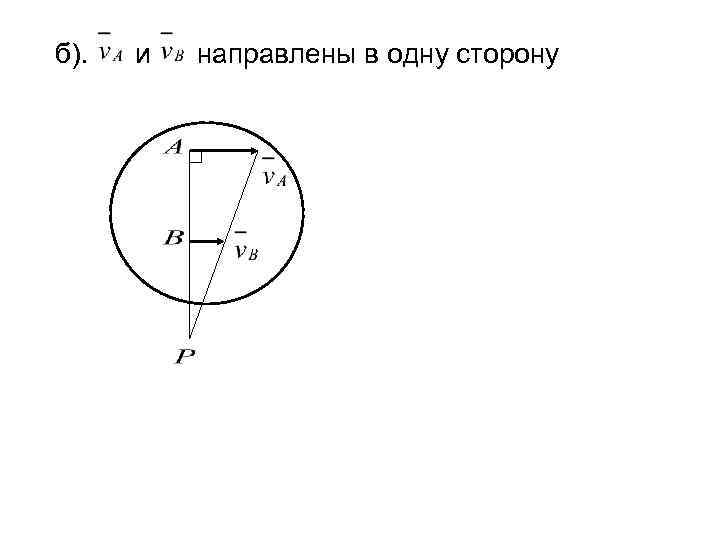
б). и направлены в одну сторону

3). II ; М. ц. с. находится в , сл. Такое движение плоской фигуры называется мгновенно поступательным.
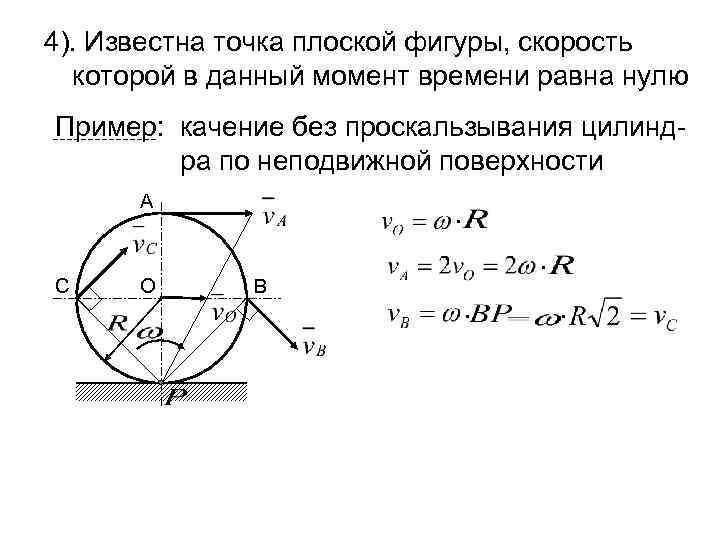
4). Известна точка плоской фигуры, скорость которой в данный момент времени равна нулю Пример: качение без проскальзывания цилиндра по неподвижной поверхности А . . С О В . .

Ускорения точек плоской фигуры Как было показано ранее т. М плоской фигуры совершает сложное движение: поступательное вместе с полюсом и вращательное вокруг полюса сл. но где Итак: . , ;

Динамика – раздел механики, в котором изучается движение тел или материальных точек под действием приложенных к ним сил. В основании динамики лежат законы, сформулированные И. Ньютоном в его классическом труде «Математические начала натуральной философии» (1687 г. ). Законы динамики I закон (закон инерции): всякая изолированная материальная точка находится либо в состоянии покоя, либо движется равномерно и прямолинейно ( открыт Галилеем в 1638 г. )

Изолированной называется м. т. , которая не взаимодействует с другими телами (м. точками) или когда действующие на нее силы взаимно уравновешиваются. Движение, совершаемое точкой при отсутствии сил, называется движением по инерции. Системы отсчета, в которых выполняется закон инерции называются инерциальными. Установить инерциальность системы отсчета можно только экспериментально. С достаточной для практики точностью, инерциальной можно считать систему отсчета, жестко связанную с Землей. Неинерциальные системы отсчета рассматриваются в общей теории относительности.

II закон (основной закон динамики): сила, действующая на м. т. , сообщает ей ускорение, которое в инерциальной системе отсчета пропорционально величине силы и направлено по этой силе. , где - масса м. т. , являющаяся мерой ее инертности. В системе СИ: ; Если на м. т. действует одновременно несколько сил, то:

III закон (закон равенства действия и противодействия) (IV аксиома статики): силы взаимодействия двух м. т. равны по величине и противоположны по направлению.

Дифференциальные уравнения движения материальной точки , т. к. , то Спроектируем его на оси координат а). Декартовы оси Oxyz: дифференциальные уравнения движения точки в декартовой системе координат

б). Естественные оси: дифференциальные уравнения движения точки в естественной системе координат Две основные задачи динамики точки I задача: по заданной массе и уравнениям движения м. т. определить силу, вызывающую это движение ; ;

II задача: по заданной массе и силе, действующей на м. т. , определить ее движение Сводится к решению системы трех дифференциальных уравнений: , , , где - постоянные интегрирования. Начальные условия: начальное - положение точки начальная - скорость точки

Решение системы дифференциальных уравнений зависит от вида правой части, т. е. от вида силы, действующей на точку. В общем случае и решение задачи составляет значительные математические трудности. Однако существуют группы сил, зависящие от отдельных параметров, для которых II задача динамики легко решаема: 1. 2. 3. 4. ; ; ; .