Лекция 7 Временные

Лекция 7 Временные ряды 1. Понятие временного ряда 2. Основные этапы анализа временных рядов 3. Модели DL и ADL

Временной ряд - это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы: • факторы, формирующие тенденцию ряда Т(t); • факторы, формирующие циклические колебания ряда S(t); • случайные факторы e(t) или (t). Аддитивная модель: Y(t)=Т(t)+S(t)+ (t). Мультипликативная модель: Y(t)=Т(t)*S(t)* (t).

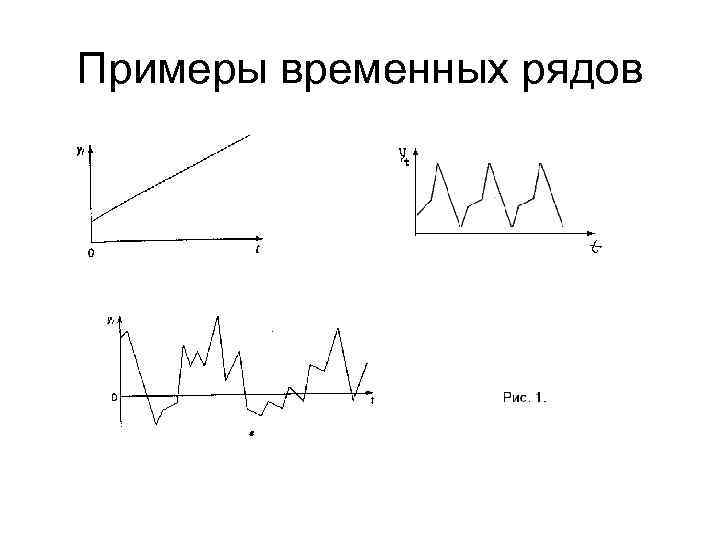
Примеры временных рядов

Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.

• Важнейшей классической задачей при исследовании экономических временных рядов является выявление и статистическая оценка основной тенденции развития изучаемого процесса и отклонения от нее.

Основные этапы анализа временных рядов: • графическое представление и описание поведения временного ряда; • выделение или удаление закономерных (неслу- чайных) составляющих временного ряда (тренда, сезонных и циклических составляющих); • сглаживание и фильтрация (удаление низко- и высокочастотных составляющих временного ряда); • исследование случайной составляющей временного ряда, построение и проверка адекватности математической модели для ее описания; • прогнозирование развития изучаемого процесса на основе имеющегося временного ряда; • исследование взаимосвязи между различными временными рядами.

Модели распределенных лагов Yt — выпуск предприятия в год t, может зависеть не только от инвестиций It в этот год, но и от инвестиций в предыдущие годы: Для статистического моделирования полезно различать два случая: Модель распределенных лагов и динамическая или авторегрессионная модель Обе модели включают в себя лагированные значения переменных, но существенно различаются с точки зрения статистического оценивания параметров.

В модели распределенных лагов (distributed lags), DL(1). В скобках указан порядок модели — максимальный лаг. Уравнение (2) является авторегрессиоинной моделью распределенных лагов или динамической моделью, ADL(1, 0). В скобках указаны максимальные лаги эндогенной (зависимой) и экзогенной (независимой) переменных.

Оператор сдвига Для аналитических вычислений с моделями, включающими лаговые переменные, удобно использовать оператор сдвига (lag operator) Так, например, модель где t=1, …, n, с использованием оператора сдвига может быть записана в более компактном виде: где A(L) и B(L) – полиномы от оператора сдвига:

Роль моделей с распределенными лагами Модели с распределенными лагами призваны сыграть большую роль в эконометрике. Адаптация экономических процессов чаще всего бывает постепенной. Так, изменение в относительной цене двух взаимозаменяемых видов сырья приводит к быстрому пересмотру методов производства. Однако полный эффект этого пересмотра проявляется лишь после обновления оборудования, которое было лучше приспособлено к использованию одного вида сырья, чем другого. Таким образом, адекватное представление фактов часто требует явного введения распределенных запаздываний.

• Нельзя правильно понять роль многочисленных мер экономической политики, если мы не знаем, когда ее эффекты начнут проявляться и когда они будут действовать в полную силу. Сюда относятся уменьшение или возрастание прямых налогов, изменение уровня учетной ставки, валютного курса и т. д

Оценивание в моделях распределенных лагов Может производиться МНК (при соблюдении всех предпосылок). Однако , если по смыслу задачи ожидается влияние с большим запаздыванием, то может оказаться, что количество коэффициентов слишком велико.

Уравнение с авторегрессионными членами может быть оценено при помощи МНК. Существенными тут являются два условия: 1) Устойчивость. Для уравнения авторег- рессии |b| < 1, лучше, если значения параметров будут отстоять на некоторое расстояние от границы критической области. 2) Отсутствует автокорреляция ошибок t.

В том случае, если ряд xi имеет некоторую структуру, например, автокорреляцию или сезонность, мы оказываемся в ситуации мультикол- линеарности. Для уменьшения числа оцениваемых параметров используют модели полиномиальных лагов (метод Алмон (Almon)) и геометрических лагов (модель Койка (Koyck)).

Выводы: Построение моделей с распределенным лагом и моделей авторегрессии имеет свою специфику: 1. Оценка параметров моделей авторегрессии, а в большинстве случаев и моделей с распределенным лагом не может быть произведена с помощью обычного МНК ввиду нарушения его предпосылок и требует специальных статистических методов. 2. Исследователям приходится решать проблемы выбора оптимальной величины лага и определения его структуры. 3. Между моделями с распределенным лагом и моделями авторегрессии существует определенная взаимосвязь, и в некоторых случаях необходимо осуществлять переход от одного типа моделей к другому.

• В динамических моделях временных рядов на зависимую переменную влияют значения независимой переменной в предыдущие периоды времени. • а) да • б) нет • в) не только

Какой МНК используется для получения оценок параметров моделей временных рядов? • а) обычный МНК • б) взвешенный МНК • в) обобщенный (ОМНК) • г) зависит от структуры ряда и выполнения основных предпосылок для модели

Вопросы для экзамена 14. Анализ вариации зависимой 1. Определение эконометрики. переменной в регрессии. 2. Этапы эконометрического 15. Гомоскедастичность и гетероске- дастичность дисперсии остатков. исследования. 16. Коэффициент детерминации R 2 3. Типы данных в эконометрическом 17. Использование статистик для исследовании. определения значимости оценок 4. Типы шкал, по которым параметров (уравнения регрессии). производятся измерения в 18. Нелинейные относительно эконометрике. включенных в анализ 5. Специфика экономических измерений. объясняющих переменных, но линейные по оцениваемым 6. Роль моделей в экономической параметрам. теории и принятии решений. 19. Регрессии нелинейные по 7. Типы эконометрических моделей. оцениваемым параметрам. 8. Линейный характер связи между 20. Отбор факторов при построении двумя экономическими факторами множественной регрессии. 9. Метод наименьших квадратов. 21. Множественная линейная 10. Предпосылки МНК. регрессия: основные понятия. 22. Фиктивные переменные. 11. Уравнения в отклонениях. 23. ОМНК. 12. Линейная регрессионная модель с 24. Использование ОМНК двумя переменными 32. Основные эл-ты временного ряда. 13. Определение качества оценок. 33. Модели DL и ADL 33. Прогнозирование.

Пример теста на установление последовательности Укажите 1. Рассчитать теоретические значения Yt последовательность по формулам для соответствующих функций. действий для 2. Построить точечные графики Y(X) по выбора оптимальной количеству функций. аппроксимирующей 3. вычислить отклонения по формуле |(Y функции -Yt. )/Y| для каждой функции. 4. Добавить на графики линии тренда для соответствующей функции. 5. Определить функцию с минимальным средним отклонением, она и будет оптимальной. 6. Для каждой функции вычислить среднее значение отклонения.