Лекция 7 Тема 8 Методы принятия решений в

Лекция 7 Тема 8. Методы принятия решений в условиях риска

Тема 8. Методы принятия решений в условиях риска 8. 1. Внутренние и внешние факторы рисков. 8. 2. Классификация рисков. 8. 3. Методы решения организационно-управленческих задач условиях риска. • Целевая функция задачи принятия решения в условиях риска. • Правило модального значения (аксиома рациональности). • Байесово правило ожидаемого значения. • Матрица решения в условиях риска, (µ, σ)-принцип. • Принцип Бернулли.

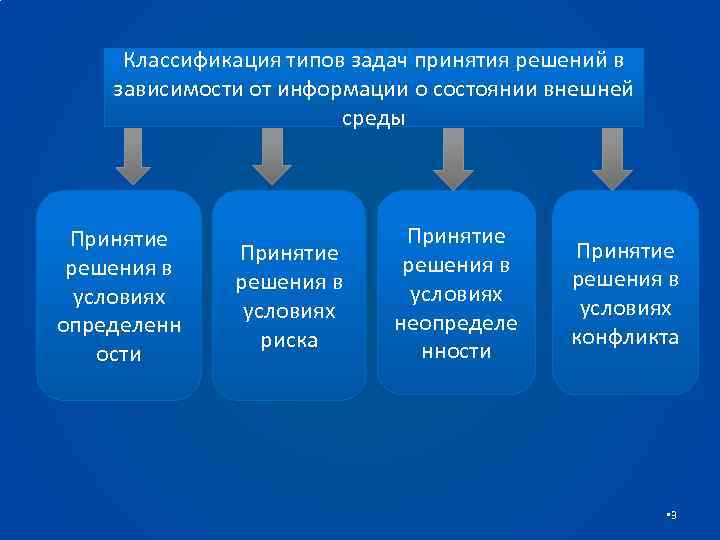Классификация типов задач принятия решений в зависимости от информации о состоянии внешней среды Принятие решения в условиях определенн ости Принятие решения в условиях риска Принятие решения в условиях неопределе нности Принятие решения в условиях конфликта • 3

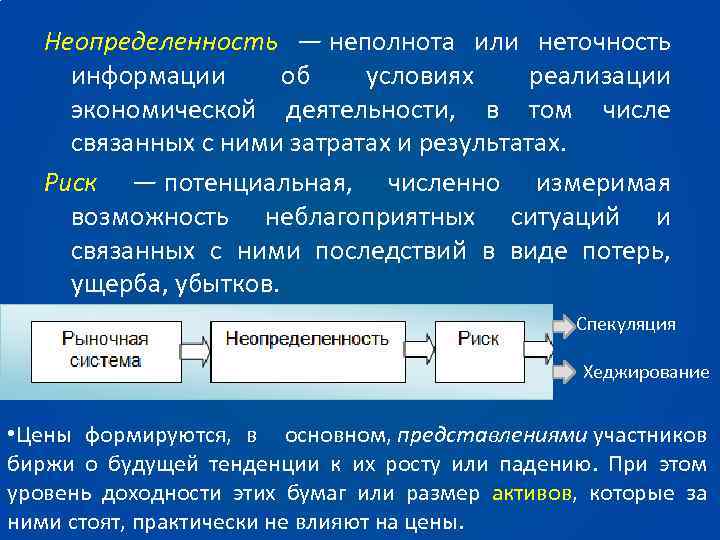Неопределенность — неполнота или неточность информации об условиях реализации экономической деятельности, в том числе связанных с ними затратах и результатах. Риск — потенциальная, численно измеримая возможность неблагоприятных ситуаций и связанных с ними последствий в виде потерь, ущерба, убытков. Спекуляция Хеджирование • Цены формируются, в основном, представлениями участников биржи о будущей тенденции к их росту или падению. При этом уровень доходности этих бумаг или размер активов, которые за ними стоят, практически не влияют на цены.

8. 1. Внешние, объективные факторы риска • законодательные и нормативно-правовые акты, которые регулируют хозяйственную и предпринимательскую деятельность; • бюджетная, финансово-кредитная и налоговая системы; • действия органов власти; • действия экономических контрагентов (поставщиков, потребителей, торговых и сбытовых посредников и т. п. ); • конкуренция; • действия криминалитета и т. п. . • политическая, экономическая, демографическая, социальная, экологическая ситуации и их изменения; • стихийные бедствия; • международные экономические связи и торговля; • инновации и т. п.

8. 1. Внутренние, субъективные факторы риска • • стратегия развития; маркетинг; производственные мощности; технологии; кадры и мотивация их деятельности; качество продукции; система управления; местоположение и т. п.

8. 2. Классификация рисков 1. По сфере проявления выделяют экономический, политический, экологический, социальный, технологический риск и т. п. . 2. По видам деятельности – ресурсный (деньги, люди, материалы), производственный, инновационный, инвестиционный, маркетинговый (коммерческий), транспортный риск и т. п. . 3. По масштабам влияния - страновой (в масштабах страны), региональный, отраслевой, риск отдельных субъектов хозяйствование. 4. По источникам возникновения - систематический или рыночный (присущ всем субъектам рынка вызванный процессами, происходящими в рыночной среде в целом); несистематический (риск отдельных субъектов хозяйствования, зависит от особенностей их деятельности).

5. Относительно самого риска - риск активной деятельности, риск пассивного ожидания. 6. По отношению источников риска к предприятию - внутренний и внешний риск. 7. По степени обоснования решений или действий - оправданный и неоправданный риски. 8. По природе риска - хозяйственный риск, риск связанный с природой человека, риск вызванный действиями естественных факторов, риск форс-мажорных обстоятельств и т. п. .

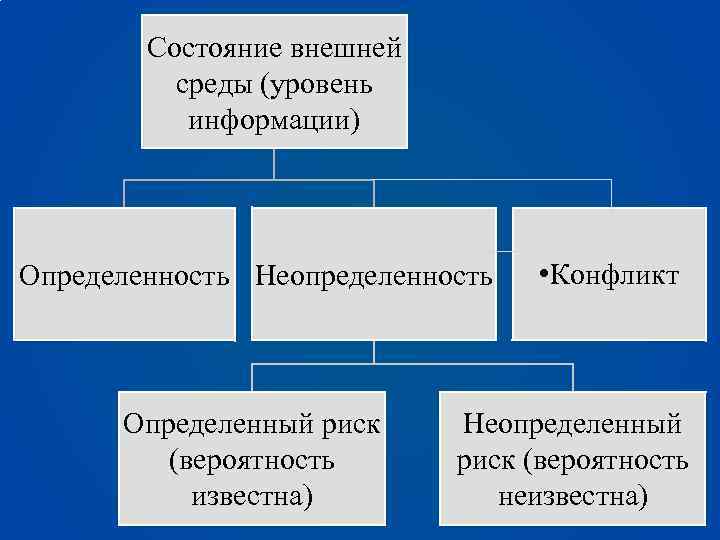Состояние внешней среды (уровень информации) Определенность Неопределенность Определенный риск (вероятность известна) • Конфликт Неопределенный риск (вероятность неизвестна)

Принятие решения в условиях риска • Принятие решения в условиях риска означает, что управляющая подсистема имеет информацию стохастического характера о поведении среды (например ей известно распределение вероятностей на множестве состояний среды). • Например, модели задач, основанные на оценке математического ожидания и среднеквадратического отклонения оцениваемой величины. • 10

Структура риска • Риск вызванный воздействием на принимаемое решение внешней среды. • Ценностный риск - определяется субъективными характеристиками ЛПР.

8. 3. Правила принятия решений в случае риска: Ш правило модального значения; Ш правило принятия решений по Байесу (µ — принцип); Ш (µ, σ) — принцип; Ш принцип принятия решений по Бернулли.

Правило модального значения (аксиома рациональности) Состояние среды Вероятность появления А 1 А 2 А 3 Р 1 Р 2 Р 3 Р 4 Р 5 Р 6 Р 7 Р 8 Р 9 Р 10 0, 14 0, 10 0, 06 0, 08 0, 07 0, 15 0, 13 0, 12 0, 07 0, 08 5 10 11 4 4 3 4 6 7 5 7 7 1 2 1 6 5 3 8 9 7 6 8 7 10 13 12 3 5 4 • Состояние среды Р 6 имеет наибольшую вероятность 0, 15 и в соответствии с правилом должна быть выбрана альтернатива А 1, дающая результат, равный 6. Однако состояние среды Р 1, имеющее незначительно меньшую вероятность появления 0, 14, для альтернатив А 2 и А 3 дает заметно лучший результат. Поэтому целесообразность выбора альтернативы А 1 может вызывать сомнения.

• В соответствии с правилом модального значения учитываются только те результаты, вероятность появления которых максимальна. • Недостатки: q ряд состояний имеют равную вероятность появления; q максимальный результат дают несколько альтернатив; q вероятность появления модального значения при одном из состояний среды только незначительно выше, чем для других состояний среды, при этом другие альтернативы оказываются более оптимальными, иногда значительно.

Байесово правило ожидаемого значения Состояние среды Р 1 Р 2 Р 3 Р 4 Р 5 Р 6 Р 7 Р 8 Р 9 Р 10 Вероятность появления 0, 14 0, 10 0, 06 0, 08 0, 07 0, 15 0, 13 0, 12 0, 07 0, 08 А 1 А 2 А 3 0, 70 1, 40 1, 54 0, 3 0, 24 0, 56 0, 40 0, 56 0, 07 0, 14 0, 07 0, 90 0, 75 0, 45 1, 04 1, 17 0, 91 0, 72 0, 96 0, 84 0, 07 0, 91 0, 84 0, 24 0, 40 0, 32 Сумма 4, 78 7, 05 5, 25 • Правило Байеса в отличие от предыдущего вовлекает в процесс выбора решения все имеющиеся значения.

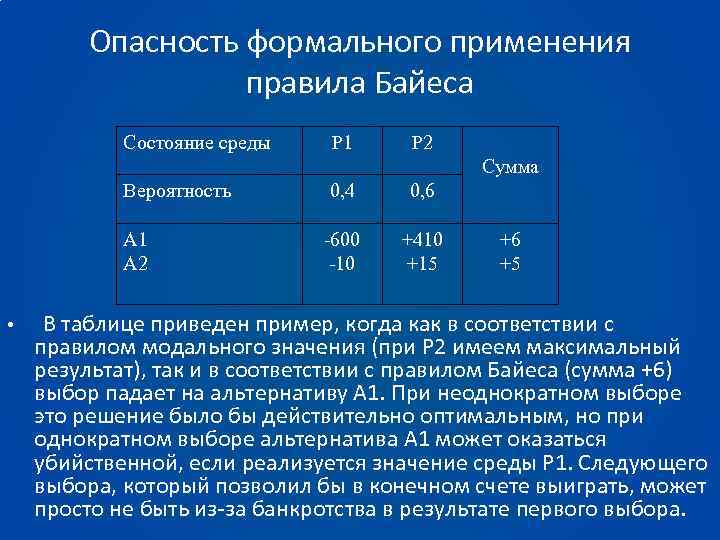Опасность формального применения правила Байеса Состояние среды Р 1 Р 2 Сумма Вероятность 0, 6 А 1 А 2 • 0, 4 -600 -10 +410 +15 +6 +5 В таблице приведен пример, когда как в соответствии с правилом модального значения (при Р 2 имеем максимальный результат), так и в соответствии с правилом Байеса (сумма +6) выбор падает на альтернативу А 1. При неоднократном выборе это решение было бы действительно оптимальным, но при однократном выборе альтернатива А 1 может оказаться убийственной, если реализуется значение среды Р 1. Следующего выбора, который позволил бы в конечном счете выиграть, может просто не быть из-за банкротства в результате первого выбора.

• То мас Ба йес (1702 — 1761) — английский математик и священник.

Математическая запись правила принятия решений по Байесу Формула учитывает суммарную степень важности ожидаемого результата при различных состояниях внешней среды, где aij – альтернативы с соответствующей вероятностью pij; Сумма дает ожидаемое значение µ : Затем выбирается та альтернатива, которая имеет наивысшее значение математического ожидания.

(µ, σ)-принцип Решение наряду с математическим ожиданием зависит от среднего квадратического отклонения σ: которое должно оцениваться как мера дисперсии.

Матрица решения в условиях риска, (µ, σ) -принцип Состояние внешней p p 1 2 3 среды p 0, 3 0, 5 0, 2 µ σ Альтернативы а 1 а 2 90 110 150 112 20, 9 95 105 120 105 8, 7

Принцип Бернулли: «ценность вещей определяется не их ценой, а их полезностью» . Т. е. каждому отдельному результату eij приписывается полезность п(eij). Тогда решение принимается в соответствии с максимизируемым значением математического ожидания полезности: Если функция полезности п(eij) линейная (выпуклая, вогнутая) , то имеет место нейтральность (склонность, несклонность по отношению к риску).

Дании л Берну лли (1700 -1782) - швейцарский физик- универсал, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук.

• Преимущество этого подхода заключается в учете индивидуальных предпочтений ЛПР. • Недостаток правила связан с тем, что функция полезности должна быть определена настолько точно, чтобы быть справедливой для ЛПР и в других ситуациях.

Управление риском • Рассмотрим особенности управления риском на историческом примере оценки опасности нападения морских пиратов — подход Бернулли и подход Колумба. Четверть тысячелетия тому назад Бернулли обнаружил возможность при страховании торговых судов снижать страховой тариф. За счет низкого тарифа он привлекал клиентов, а за счет большого числа клиентов мог с достаточной точностью рассчитывать вероятность потерь и получать приличную прибыль.

• Четвертью тысячелетия ранее Колумб отправился на поиски пути в Индию. Для его кораблей, как и для торговых судов времен Бернулли, главную угрозу представляли пираты. Вероятность нападения пиратов высока. Но нужно ли было Колумбу знать величину этой вероятности? Колумб оснастил свои корабли прямоугольными парусами с максимальной площадью. Он потерял в маневренности, но существенно увеличил скорость каравана.

Принятие решения в условиях риска. Пример: выбор варианта продаваемого товара Фирма А может выставить на продажу один из товаров Т 1 или Т 2, а фирма В – один из товаров Т 1’, Т 2’, Т 3’. Товары Т 1 и Т 1’ являются конкурирующими (например, пиво и лимонад), товары Т 1 и Т 3’ – дополнительными (например, пиво и вобла); остальные пары товаров практически нейтральны. Прибыль фирмы А зависит от сочетания товаров, выставляемых на продажу обеими фирмами, и определяется таблицей 1. Известно, что фирма В выставляет на продажу товар Т 3’ в три раза реже, чем Т 1’ и в четыре раза реже, чем Т 2’. Какой товар следует выставить на продажу фирме А?

Выбор варианта продаваемого товара в условиях риска. Решение примера Т 1’(p=3/8) Т 2’(p=4/8) Т 3’(p=1/8) Т 1 8 18 40 Т 2 18 15 14 Найдем математические ожидания МТ 1=8*3/8+ 18*4/8+40*1/8=17, МТ 2=18*3/8+15*4/8+14*1/8=16. Оптимальной является альтернатива Т 1.

Выводы по теме 8: 1. Риск—потенциальная, численно измеримая возможность неблагоприятных ситуаций и связанных с ними последствий в виде потерь, ущерба, убытков. 2. Риск характеризуется внешними – объективными и внутренними - субъективными причинами. Последнюю составляющую еще называют ценностным риском определяемым ЛПР. 3. Целевая функция задачи принятия решения в условиях риска есть композиция функции реализации и оценочной функции с учетом влияния степени риска. 4. Классические правила принятия решений в условиях риска (правило модального значения, Байесово правило ожидаемого значения, (µ, σ)-принцип, принцип Бернулли) широко используются в практике принятия решений.