Лекция № 7 Солодухин Е. А.

Лекция № 7 Солодухин Е. А.

Метрические задачи

Метрическими называются задачи, в ходе решения которых определяется значение измеряемой величины – расстояния между двумя точками (длина отрезка), величины линейного угла или истинной формы и размеров плоской фигуры. Решение метрических задач основывается только на методе прямоугольного проециро- вания.

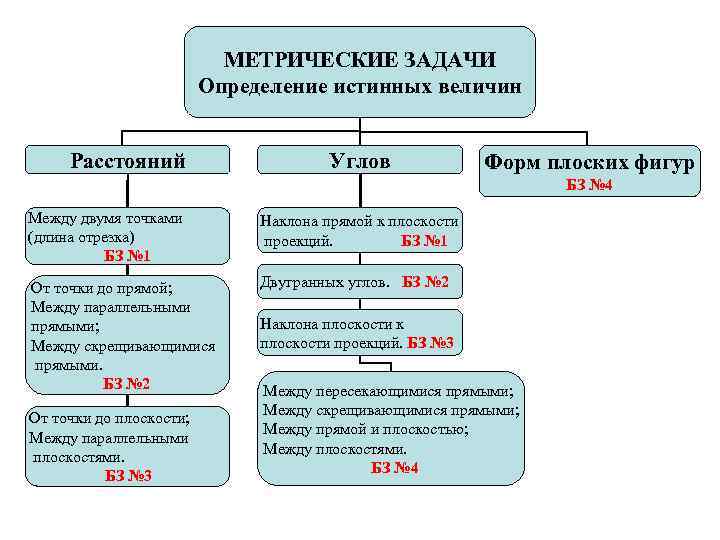
МЕТРИЧЕСКИЕ ЗАДАЧИ Определение истинных величин Расстояний Углов Форм плоских фигур БЗ № 4 Между двумя точками Наклона прямой к плоскости (длина отрезка) проекций. БЗ № 1 От точки до прямой; Двугранных углов. БЗ № 2 Между параллельными прямыми; Наклона плоскости к Между скрещивающимися плоскости проекций. БЗ № 3 прямыми. БЗ № 2 Между пересекающимися прямыми; Между скрещивающимися прямыми; От точки до плоскости; Между прямой и плоскостью; Между параллельными Между плоскостями. БЗ № 4 БЗ № 3

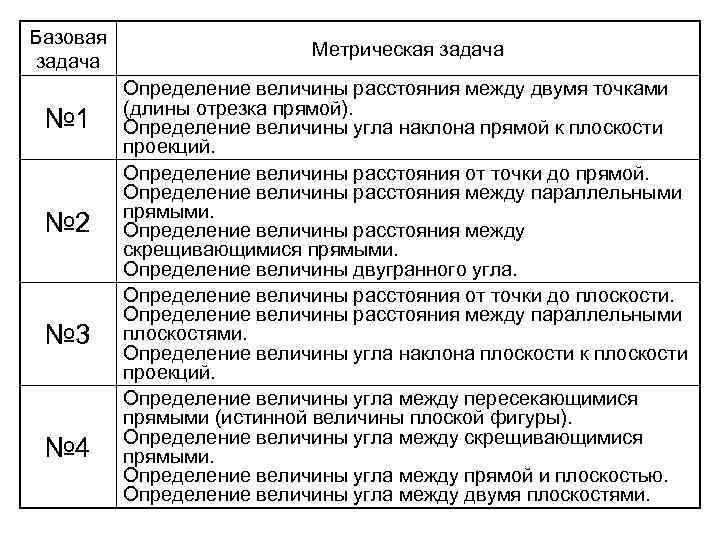
Базовая Метрическая задача Определение величины расстояния между двумя точками (длины отрезка прямой). № 1 Определение величины угла наклона прямой к плоскости проекций. Определение величины расстояния от точки до прямой. Определение величины расстояния между параллельными прямыми. № 2 Определение величины расстояния между скрещивающимися прямыми. Определение величины двугранного угла. Определение величины расстояния от точки до плоскости. Определение величины расстояния между параллельными № 3 плоскостями. Определение величины угла наклона плоскости к плоскости проекций. Определение величины угла между пересекающимися прямыми (истинной величины плоской фигуры). Определение величины угла между скрещивающимися № 4 прямыми. Определение величины угла между прямой и плоскостью. Определение величины угла между двумя плоскостями.

Метрические задачи, в основе решения которых лежит базовая задача № 1

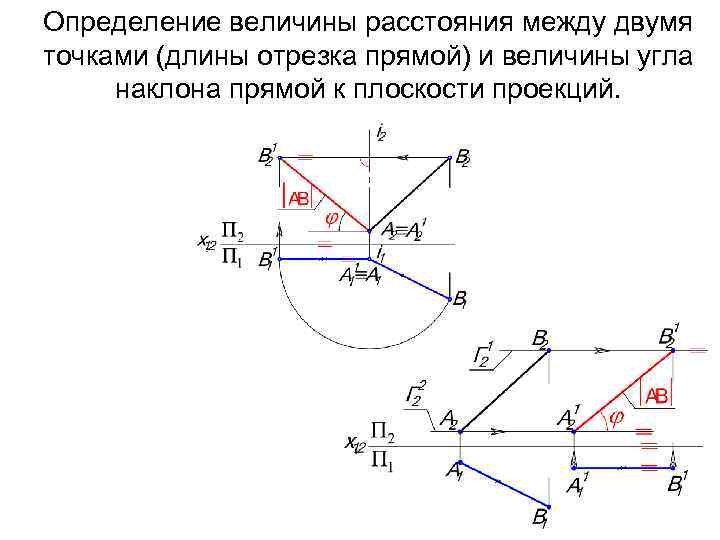
Определение величины расстояния между двумя точками (длины отрезка прямой) и величины угла наклона прямой к плоскости проекций.

Метрические задачи, в основе решения которых лежит базовая задача № 2

Определение величины расстояния от точки до прямой и между параллельными прямыми

Определение величины расстояния между скрещивающимися прямыми Выбирается одна из двух заданных прямых ( на примере это прямая l) и преобразовывается в проецирующую прямую. Вторая прямая (на примере прямая m) перестраивается совместно с первой прямой.

Определение величины двугранного угла Ребро АВ двугранного угла (ABCD) преобразовывается в проецирующую прямую. Две другие точки C и D перестраиваются совместно с ребром АВ.

Метрические задачи, в основе решения которых лежит базовая задача № 3

Определение величины угла наклона плоскости к плоскости проекций и расстояния от точки до плоскости Задано: Т(ΔАВС) и точка D. Определить: величины DE=(D, T); DE T и ∠φ=(T^П 2). П 2=const П 1 → П 4 Х 1, 2(П 1/П 2) → Х 2, 4(П 2/П 4) П 4 Т и П 4 П 2 П 4 f, f⊂T ∠φ=(T 4^ x 2, 4) DE T D 4 E 4 T 4 и (D 4 E 4)=ⅼDEⅼ

Определение величины расстояния между параллельными плоскостями Задано: Т(ΔАВС) ‖ Λ(m, n). Определить: величину DE=(Λ, T) Выбираем П 2=const П 1 → П 4 Х 1, 2(П 1/П 2) → Х 2, 4(П 2/П 4) (П 4 Т и П 4 Λ) и П 4 П 2 П 4 f, f⊂T DE T и DE Λ D 4 E 4 T 4 и D 4 E 4 Λ 4 (D 4 E 4)=ⅼDEⅼ

Метрические задачи, в основе решения которых лежит базовая задача № 4

Определение величины угла между пересекающимися прямыми (истинной величины плоской фигуры) Задано: пересекающиеся прямые “m” и “n”. Определить: величину угла между прямыми “m” и “n”. Решение задачи выполняется способом вращения вокруг прямой уровня. На примере это вращение вокруг горизонтали.

Задано: пересекающиеся прямые “m” и “n”. Определить: величину угла между прямыми “m” и “n”. Решение задачи выполняется способом перемены плоскостей проекций.

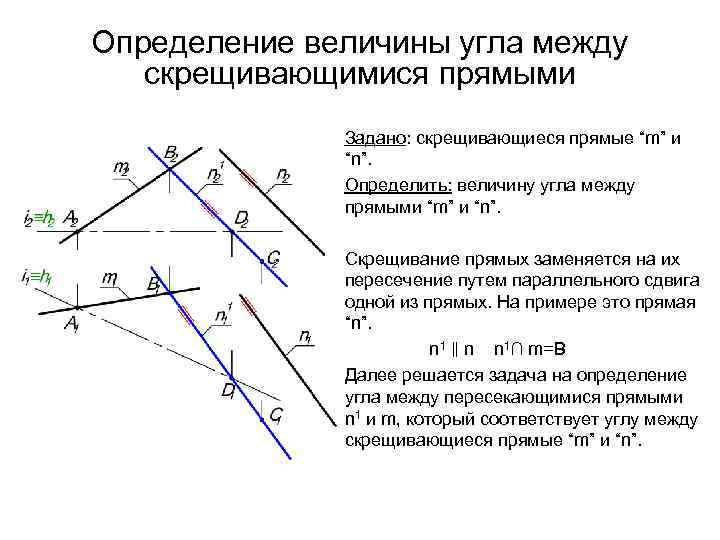
Определение величины угла между скрещивающимися прямыми Задано: скрещивающиеся прямые “m” и “n”. Определить: величину угла между прямыми “m” и “n”. Скрещивание прямых заменяется на их пересечение путем параллельного сдвига одной из прямых. На примере это прямая “n”. n 1 ‖ n n 1∩ m=B Далее решается задача на определение угла между пересекающимися прямыми n 1 и m, который соответствует углу между скрещивающиеся прямые “m” и “n”.