лекция 7 - Синтез КС на DС и СD.pptx
- Количество слайдов: 16

Лекция 7 Синтез комбинационных схем на дешифраторах
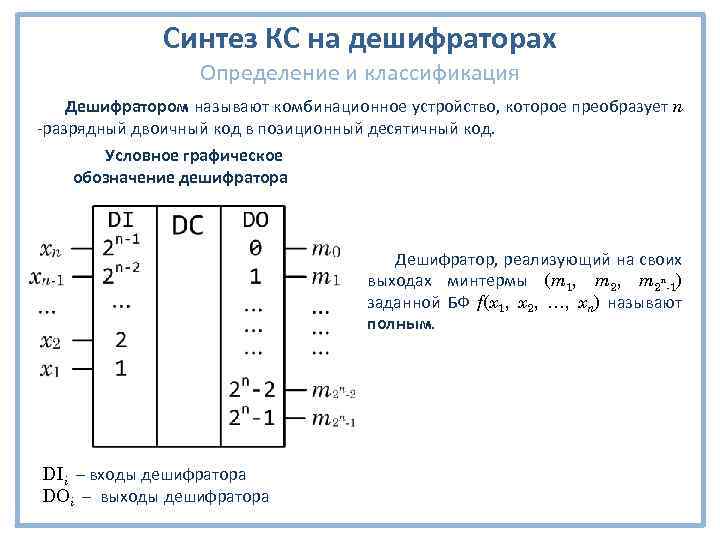
Синтез КС на дешифраторах Определение и классификация Дешифратором называют комбинационное устройство, которое преобразует n -разрядный двоичный код в позиционный десятичный код. Условное графическое обозначение дешифратора Дешифратор, реализующий на своих выходах минтермы (m 1, m 2 n-1) заданной БФ f(x 1, x 2, …, xn) называют полным. DIi – входы дешифратора DOi – выходы дешифратора
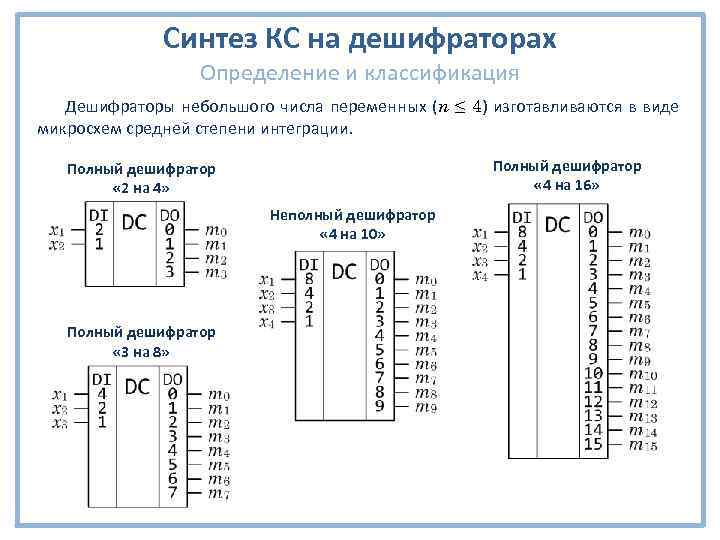
Синтез КС на дешифраторах Определение и классификация Дешифраторы небольшого числа переменных (n ≤ 4) изготавливаются в виде микросхем средней степени интеграции. Полный дешифратор « 4 на 16» Полный дешифратор « 2 на 4» Неполный дешифратор « 4 на 10» Полный дешифратор « 3 на 8»
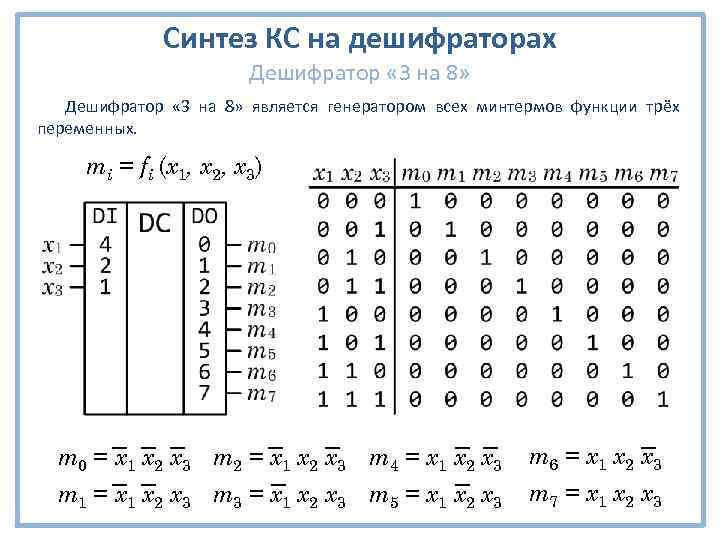
Синтез КС на дешифраторах Дешифратор « 3 на 8» является генератором всех минтермов функции трёх переменных. mi = fi (x 1, x 2, x 3) m 0 = x 1 x 2 x 3 m 2 = x 1 x 2 x 3 m 4 = x 1 x 2 x 3 m 6 = x 1 x 2 x 3 m 1 = x 1 x 2 x 3 m 3 = x 1 x 2 x 3 m 5 = x 1 x 2 x 3 m 7 = x 1 x 2 x 3

Синтез КС на дешифраторах Синтез КС на дешифраторе « 3 на 8» Пример 1: Задана функция трёх переменных в дизъюнктивной нормальной форме: (1) f (x 1, x 2, x 3) = x 1 x 2 x 3 + x 1 x 2 Необходимо спроектировать схему, реализующую f(x 1, x 2, x 3) с использованием дешифратора « 3 на 8» . Используя правило расширения БФ, представим (1) в СДНФ: f (x 1, x 2, x 3) = x 1 x 2 x 3 + x 2 x 3(x 1 + x 1) + x 1 x 2(x 3 + x 3) = = x 1 x 2 x 3 + x 1 x 2 x 3 Если входы дешифратора запитать переменными x 1, x 2, x 3, то для реализации требуемой функции следует задействовать следующие выходы дешифратора: m 0 = x 1 x 2 x 3 m 3 = x 1 x 2 x 3 m 6 = x 1 x 2 x 3 m 7 = x 1 x 2 x 3

Синтез КС на дешифраторах Синтез КС на дешифраторе « 3 на 8» Совершенная дизъюнктивная нормальная форма (СДНФ) f (x 1, x 2, x 3) : f (x 1, x 2, x 3) = m 0 + m 5 + m 6 + m 7 = Σm(0, 3, 6, 7) Реализация этой функции с использованием дешифратора « 3 на 8» : Таким образом, любая функция трёх переменных, представленная в СДНФ или таблицей истинности, может быть реализована на дешифраторе « 3 на 8» и элементе ИЛИ.
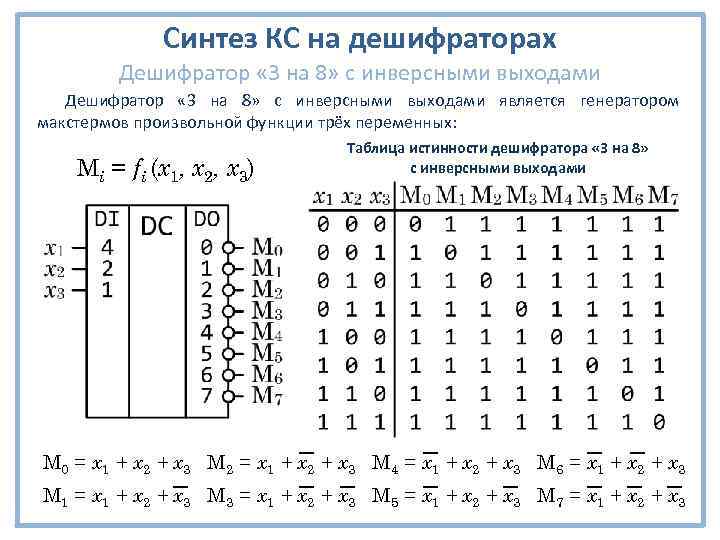
Синтез КС на дешифраторах Дешифратор « 3 на 8» c инверсными выходами Дешифратор « 3 на 8» с инверсными выходами является генератором макстермов произвольной функции трёх переменных: Mi = fi (x 1, x 2, x 3) Таблица истинности дешифратора « 3 на 8» с инверсными выходами M 0 = x 1 + x 2 + x 3 M 2 = x 1 + x 2 + x 3 M 4 = x 1 + x 2 + x 3 M 6 = x 1 + x 2 + x 3 M 1 = x 1 + x 2 + x 3 M 3 = x 1 + x 2 + x 3 M 5 = x 1 + x 2 + x 3 M 7 = x 1 + x 2 + x 3
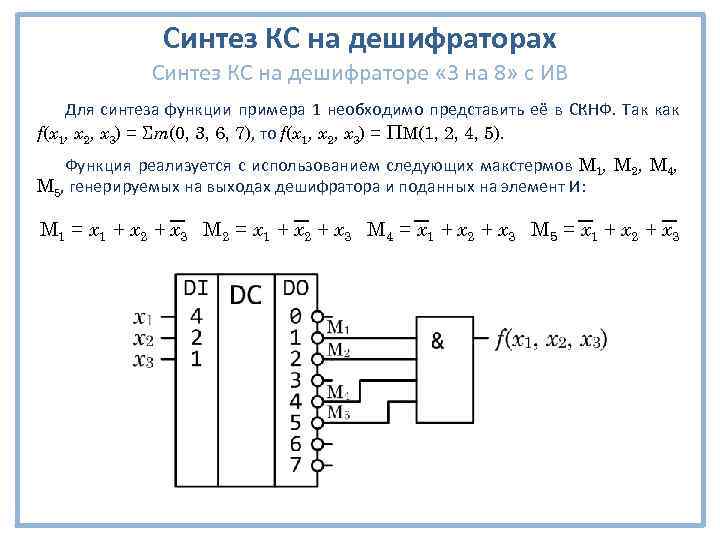
Синтез КС на дешифраторах Синтез КС на дешифраторе « 3 на 8» с ИВ Для синтеза функции примера 1 необходимо представить её в СКНФ. Так как f(x 1, x 2, x 3) = Σm(0, 3, 6, 7), то f(x 1, x 2, x 3) = ΠM(1, 2, 4, 5). Функция реализуется с использованием следующих макстермов M 1, M 2, M 4, M 5, генерируемых на выходах дешифратора и поданных на элемент И: M 1 = x 1 + x 2 + x 3 M 2 = x 1 + x 2 + x 3 M 4 = x 1 + x 2 + x 3 M 5 = x 1 + x 2 + x 3
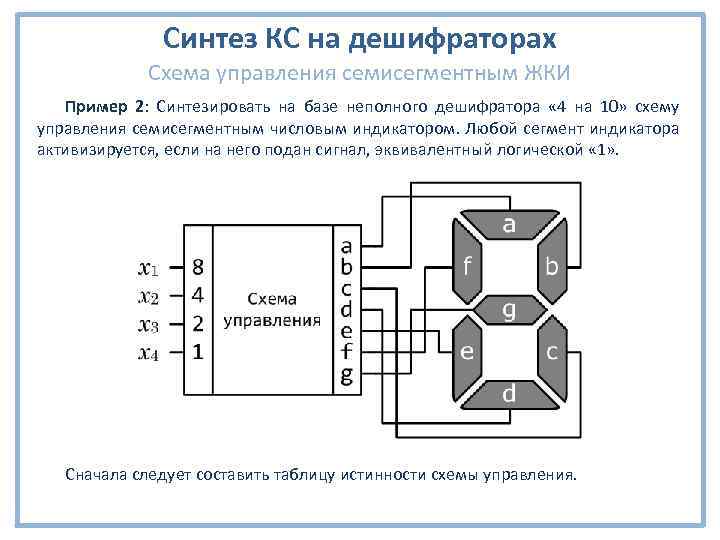
Синтез КС на дешифраторах Схема управления семисегментным ЖКИ Пример 2: Синтезировать на базе неполного дешифратора « 4 на 10» схему управления семисегментным числовым индикатором. Любой сегмент индикатора активизируется, если на него подан сигнал, эквивалентный логической « 1» . Сначала следует составить таблицу истинности схемы управления.

Синтез КС на дешифраторах Схема управления семисегментным ЖКИ Таблица истинности схемы управления Функции управления a = M 1∙M 4 b = M 5∙M 6 c = M 2 d = M 1∙M 4∙M 7 = a∙M 7 e = M 1∙M 3∙M 4∙M 5∙M 7∙M 9 = = d∙M 3∙M 5∙M 9 f = M 1∙M 2∙M 3∙M 7 g = M 0∙M 1∙M 7
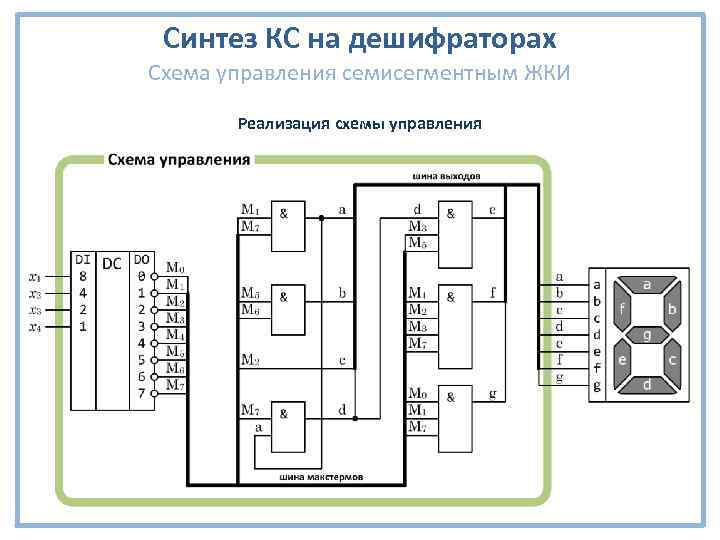
Синтез КС на дешифраторах Схема управления семисегментным ЖКИ Реализация схемы управления
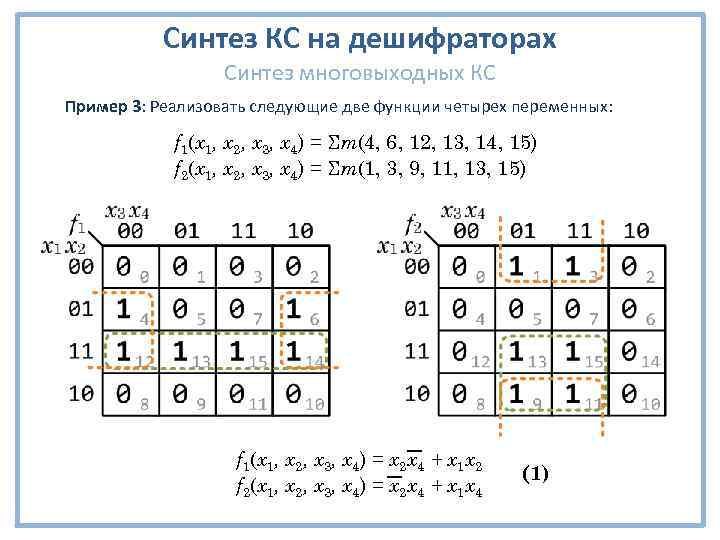
Синтез КС на дешифраторах Синтез многовыходных КС Пример 3: Реализовать следующие две функции четырех переменных: f 1(x 1, x 2, x 3, x 4) = Σm(4, 6, 12, 13, 14, 15) f 2(x 1, x 2, x 3, x 4) = Σm(1, 3, 9, 11, 13, 15) f 1(x 1, x 2, x 3, x 4) = x 2 x 4 + x 1 x 2 f 2(x 1, x 2, x 3, x 4) = x 2 x 4 + x 1 x 4 (1)
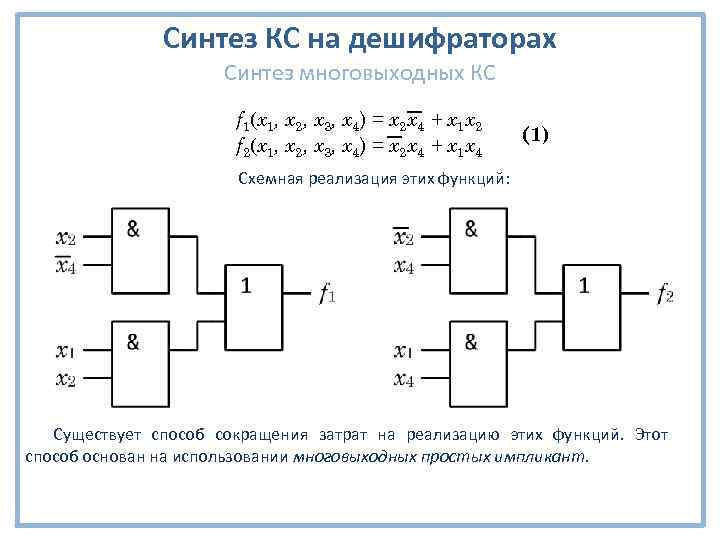
Синтез КС на дешифраторах Синтез многовыходных КС f 1(x 1, x 2, x 3, x 4) = x 2 x 4 + x 1 x 2 f 2(x 1, x 2, x 3, x 4) = x 2 x 4 + x 1 x 4 (1) Схемная реализация этих функций: Существует способ сокращения затрат на реализацию этих функций. Этот способ основан на использовании многовыходных простых импликант.
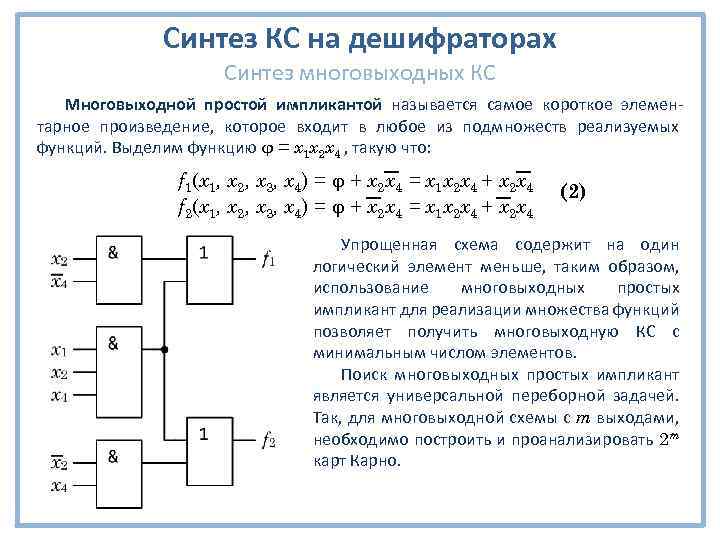
Синтез КС на дешифраторах Синтез многовыходных КС Многовыходной простой импликантой называется самое короткое элементарное произведение, которое входит в любое из подмножеств реализуемых функций. Выделим функцию φ = x 1 x 2 x 4 , такую что: f 1(x 1, x 2, x 3, x 4) = φ + x 2 x 4 = x 1 x 2 x 4 + x 2 x 4 f 2(x 1, x 2, x 3, x 4) = φ + x 2 x 4 = x 1 x 2 x 4 + x 2 x 4 (2) Упрощенная схема содержит на один логический элемент меньше, таким образом, использование многовыходных простых импликант для реализации множества функций позволяет получить многовыходную КС с минимальным числом элементов. Поиск многовыходных простых импликант является универсальной переборной задачей. Так, для многовыходной схемы с m выходами, необходимо построить и проанализировать 2 m карт Карно.

Синтез КС на дешифраторах Синтез многовыходных КС При реализации функций (1) на дешифраторе следует задействовать следующие минтермы: f 1(x 1, x 2, x 3, x 4) = x 2 x 4 + x 1 x 2 = (x 1 + x 1)x 2 x 4 + (x 4 + x 4)x 1 x 2 = = x 1 x 2 x 4 + x 1 x 2 x 4 = x 1 x 2 x 4 + x 1 x 2 x 4 f 2(x 1, x 2, x 3, x 4) = x 2 x 4 + x 1 x 4 = (x 1 + x 1)x 2 x 4 + (x 2 + x 2)x 1 x 4 = (3) = x 1 x 2 x 4 + x 1 x 2 x 4 = x 1 x 2 x 4 + x 1 x 2 x 4 Получилось так, что обе функции не зависят от переменной x 3, следовательно минтермы включают в себя только переменные x 1, x 2, x 4. Для реализации функций (2) необходимо задействовать следующие минтермы: f 1(x 1, x 2, x 3, x 4) = x 1 x 2 x 4 + x 2 x 4 = x 1 x 2 x 4 + (x 1 + x 1)x 2 x 4 = = x 1 x 2 x 4 + x 1 x 2 x 4 f 2(x 1, x 2, x 3, x 4) = x 1 x 2 x 4 + x 2 x 4 = x 1 x 2 x 4 + (x 1 + x 1)x 2 x 4 = = x 1 x 2 x 4 + x 1 x 2 x 4 (4)
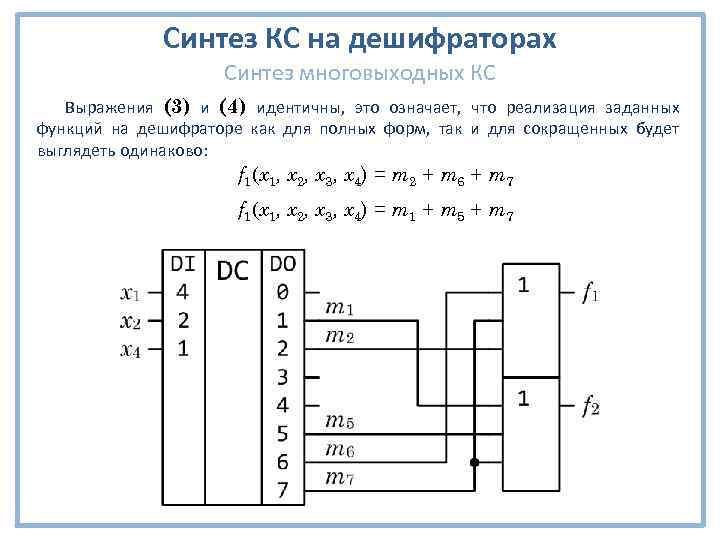
Синтез КС на дешифраторах Синтез многовыходных КС Выражения (3) и (4) идентичны, это означает, что реализация заданных функций на дешифраторе как для полных форм, так и для сокращенных будет выглядеть одинаково: f 1(x 1, x 2, x 3, x 4) = m 2 + m 6 + m 7 f 1(x 1, x 2, x 3, x 4) = m 1 + m 5 + m 7
лекция 7 - Синтез КС на DС и СD.pptx