ЛЕКЦИЯ 7 ПОВЕРХНОСТИ 1 Классификация поверхностей 2 Гранные

ЛЕКЦИЯ 7 ПОВЕРХНОСТИ 1. Классификация поверхностей. 2. Гранные поверхности и многогранники. 3. Чертежи многогранников. 4. Пересечение многогранника плоскостью. 5. Пересечение многогранника с прямой линией. 6. Взаимное пересечение многогранников.

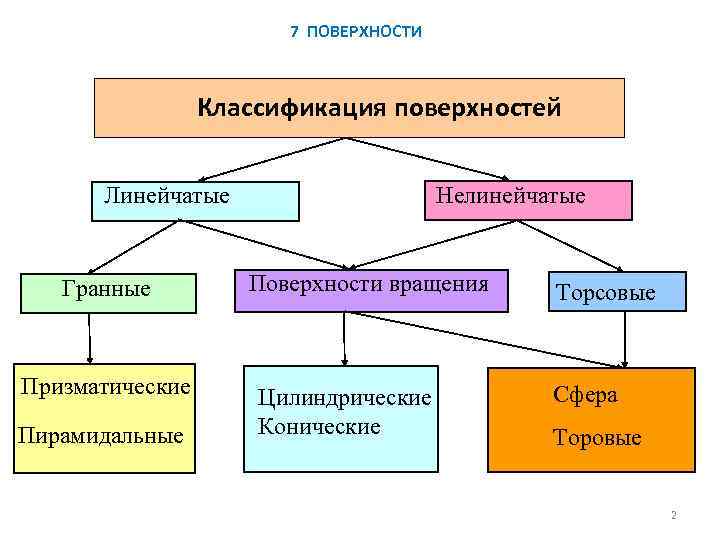7 ПОВЕРХНОСТИ Классификация поверхностей Нелинейчатые Линейчатые Гранные Призматические Пирамидальные Поверхности вращения Цилиндрические Конические Торсовые Сфера Торовые 2

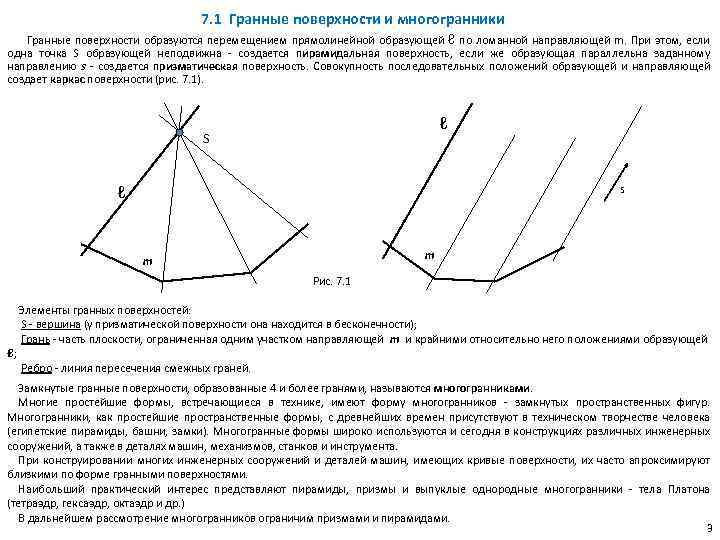7. 1 Гранные поверхности и многогранники Гранные поверхности образуются перемещением прямолинейной образующей ℓ по ломанной направляющей m. При этом, если одна точка S образующей неподвижна - создается пирамидальная поверхность, если же образующая параллельна заданному направлению s - создается призматическая поверхность. Совокупность последовательных положений образующей и направляющей создает каркас поверхности (рис. 7. 1). ℓ S ℓ s m m Рис. 7. 1 ℓ; Элементы гранных поверхностей: S - вершина (у призматической поверхности она находится в бесконечности); Грань - часть плоскости, ограниченная одним участком направляющей m и крайними относительно него положениями образующей Ребро - линия пересечения смежных граней. Замкнутые гранные поверхности, образованные 4 и более гранями, называются многогранниками. Многие простейшие формы, встречающиеся в технике, имеют форму многогранников - замкнутых пространственных фигур. Многогранники, как простейшие пространственные формы, с древнейших времен присутствуют в техническом творчестве человека (египетские пирамиды, башни, замки). Многогранные формы широко используются и сегодня в конструкциях различных инженерных сооружений, а также в деталях машин, механизмов, станков и инструмента. При конструировании многих инженерных сооружений и деталей машин, имеющих кривые поверхности, их часто апроксимируют близкими по форме гранными поверхностями. Наибольший практический интерес представляют пирамиды, призмы и выпуклые однородные многогранники - тела Платона (тетраэдр, гексаэдр, октаэдр и др. ) В дальнейшем рассмотрение многогранников ограничим призмами и пирамидами. 3

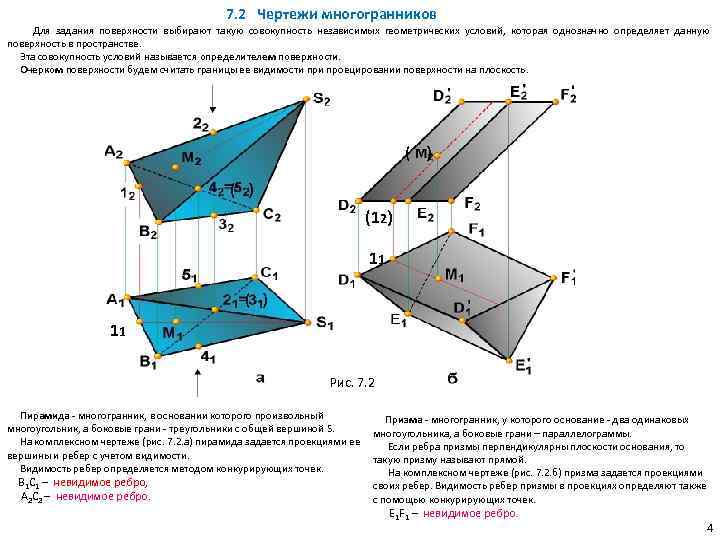7. 2 Чертежи многогранников Для задания поверхности выбирают такую совокупность независимых геометрических условий, которая однозначно определяет данную поверхность в пространстве. Эта совокупность условий называется определителем поверхности. Очерком поверхности будем считать границы ее видимости проецировании поверхности на плоскость. ( ) (12) 11 ( ) 11 Рис. 7. 2 Пирамида - многогранник, в основании которого произвольный многоугольник, а боковые грани - треугольники с общей вершиной S. На комплексном чертеже (рис. 7. 2. а) пирамида задается проекциями ее вершины и ребер с учетом видимости. Видимость ребер определяется методом конкурирующих точек. В 1 С 1 – невидимое ребро, А 2 С 2 – невидимое ребро. Призма - многогранник, у которого основание - два одинаковых многоугольника, а боковые грани – параллелограммы. Если ребра призмы перпендикулярны плоскости основания, то такую призму называют прямой. На комплексном чертеже (рис. 7. 2. б) призма задается проекциями своих ребер. Видимость ребер призмы в проекциях определяют также с помощью конкурирующих точек. Е 1 F 1 – невидимое ребро. 4

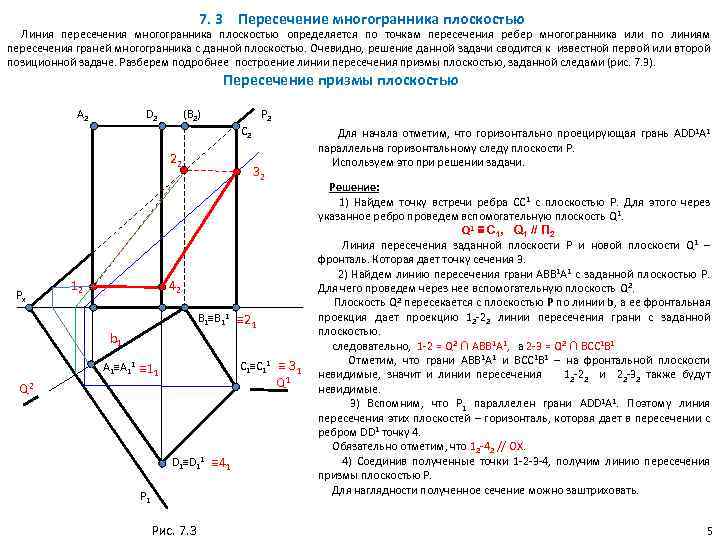7. 3 Пересечение многогранника плоскостью Линия пересечения многогранника плоскостью определяется по точкам пересечения ребер многогранника или по линиям пересечения граней многогранника с данной плоскостью. Очевидно, решение данной задачи сводится к известной первой или второй позиционной задаче. Разберем подробнее построение линии пересечения призмы плоскостью, заданной следами (рис. 7. 3). Пересечение призмы плоскостью A 2 D 2 (B 2) Р 2 C 2 22 Рх 12 Для начала отметим, что горизонтально проецирующая грань АDD 1 А 1 параллельна горизонтальному следу плоскости Р. Используем это при решении задачи. 32 42 В 1≡В 11 ≡ 21 b 1 С 1≡С 11 ≡ 31 А 1≡А 11 ≡ 11 Q 2 D 1≡D 11 ≡ 41 Р 1 Рис. 7. 3 Решение: 1) Найдем точку встречи ребра СС 1 с плоскостью Р. Для этого через указанное ребро проведем вспомогательную плоскость Q 1 ≡ C 1, Q 1 // П 2 Линия пересечения заданной плоскости Р и новой плоскости Q 1 – фронталь. Которая дает точку сечения 3. 2) Найдем линию пересечения грани АВВ 1 А 1 с заданной плоскостью Р. Для чего проведем через нее вспомогательную плоскость Q 2. Плоскость Q 2 пересекается с плоскостью Р по линии b, а ее фронтальная проекция дает проекцию 12 -22 линии пересечения грани с заданной плоскостью. следовательно, 1 -2 = Q 2 ∩ АВВ 1 А 1, а 2 -3 = Q 2 ∩ ВСС 1 В 1 Отметим, что грани АВВ 1 А 1 и ВСС 1 В 1 – на фронтальной плоскости невидимые, значит и линии пересечения 12 -22 и 22 -32 также будут невидимые. 3) Вспомним, что Р 1 параллелен грани АDD 1 А 1. Поэтому линия пересечения этих плоскостей – горизонталь, которая дает в пересечении с ребром DD 1 точку 4. Обязательно отметим, что 12 -42 // ОХ. 4) Соединив полученные точки 1 -2 -3 -4, получим линию пересечения призмы плоскостью Р. Для наглядности полученное сечение можно заштриховать. 5

Пересечение пирамиды плоскостью Решение типовой задачи на пересечение пирамиды плоскостью существенно облегчается, если найти точки пересечения каждого ребра пирамиды с заданной плоскостью, т. е. многократно решить 1 -ю позиционную задачу. S 2 Для этого можно воспользоваться алгоритмом, примененным нами ранее, при решении 1 -й позиционной задачи на рис. 4. 4. Однако, удобнее применить преобразование чертежа. Рассмотрим второй вариант. Р 2 К 2 32 22 42 Х Рх 12 21 31 11 41 Р 1 14 Х 1 24 44 34 К 4 Решение: 1) Заменой плоскостей проекций преобразовать чертеж так, чтобы плоскость Р заняла проецирующее положение (рис. 7. 4). ОХ 1 Р 1. Точку К возьмем произвольно на следе плоскости Р. Построим новое положение следа плоскости Р на П 4. 2) Найдем точки пересечения всех ребер пирамиды с плоскостью Р. 3) Обозначим полученные точки и перенесем их на заданные плоскости проекций П 1 и П 2. Отметим 14, 24, 34, 44. 4) По линии связи найдем горизонтальные и фронтальные проекции полученных точек. Соединим точки и получим многоугольник сечения. S 4 Рис. 7. 4 6

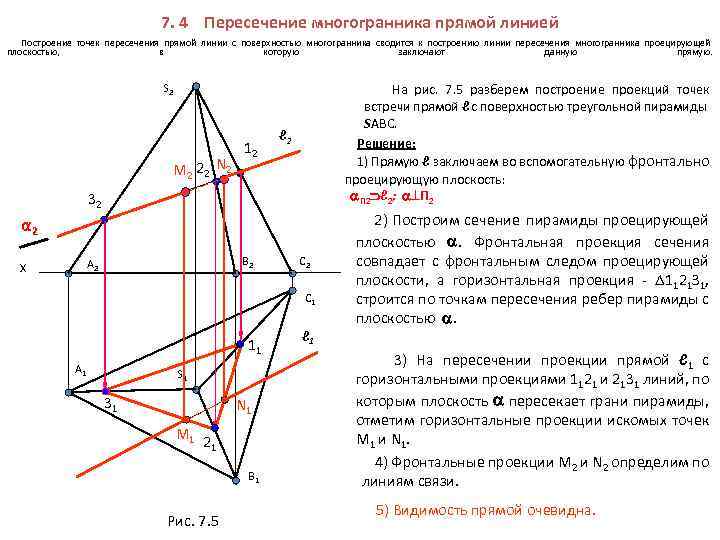7. 4 Пересечение многогранника прямой линией Построение точек пересечения прямой линии с поверхностью многогранника сводится к построению линии пересечения многогранника проецирующей плоскостью, в которую заключают данную прямую. На рис. 7. 5 разберем построение проекций точек встречи прямой ℓ с поверхностью треугольной пирамиды SАВС. Решение: 1) Прямую ℓ заключаем во вспомогательную фронтально проецирующую плоскость: П 2 ℓ 2; П 2 S 2 М 2 2 2 N 2 12 ℓ 2 32 α 2 В 2 А 2 Х С 2 С 1 11 А 1 S 1 31 N 1 М 1 21 В 1 Рис. 7. 5 ℓ 1 2) Построим сечение пирамиды проецирующей плоскостью . Фронтальная проекция сечения совпадает с фронтальным следом проецирующей плоскости, а горизонтальная проекция - 1121 З 1, строится по точкам пересечения ребер пирамиды с плоскостью . 3) На пересечении проекции прямой ℓ 1 с горизонтальными проекциями 1121 и 2131 линий, по которым плоскость пересекает грани пирамиды, отметим горизонтальные проекции искомых точек М 1 и N 1. 4) Фронтальные проекции М 2 и N 2 определим по линиям связи. 5) Видимость прямой очевидна.

7. 5 Взаимное пересечение многогранников Линия пересечения двух многогранников может быть определена по точкам пересечения ребер одного многогранника с гранями другого; это - известная задача на определение точки пересечения прямой с плоскостью. Линия пересечения многогранников может быть определена и как линия пересечения граней многогранников: это – известная задача на определение линии пересечения двух плоскостей. В зависимости от условия задачи применяют тот или иной способ, или эти два способа часто комбинируют (рис. 7. 6). B 2 Решение: 12 22 72 S 2 52 C 2 62 A 2 82 Х 42 32 A 1 31 41 71≡ 81 11 Р 1 S 1 21 51≡ 61 B 1 C 1 Г 1 Рис. 7. 6 Для начала отметим точки 1, 2, 3 и 4 пересечения ребер пирамиды с гранями призмы. Обозначим ребра пирамиды. 1) Выбираем одну из боковых граней призмы и определяем линию пересечения этой грани с гранями пирамиды. Горизонтально проецирующая плоскость Г этой боковой грани призмы пересекается с гранями пирамиды по треугольнику. Отрезки 5 -2, 2 -4, 4 -6 сторон этого треугольника, принадлежащие граням пирамиды, являются сторонами искомого многоугольника сечения. 2) Горизонтально проецирующая плоскость Р второй боковой грани призмы пересекается с пирамидой также по треугольнику. Отрезки 3 -7 и 3 -8 сторон этого треугольника представляют также стороны пространственного многоугольника пересечения заданных многогранников. 3) Горизонтально проецирующая плоскость Q третьей грани призмы пересекает пирамиду уже по четырехугольнику. Отрезки 1 -5, 1 -7 и 6 -8 принадлежат граням многогранников - призмы и пирамиды. Они также являются сторонами многоугольника пересечения. 4) Определим видимость пространственного многоугольника пересечения в проекциях. Отрезки 5 -2, 1 -5, 6 -8 и 4 -6 видимы во фронтальной проекции. Каждый из них принадлежит видимым граням многогранников. Отрезки 1 -7, 7 -3, 3 -8 и 2 -4 во фронтальной проекции невидимы. После этого нетрудно определить и видимость участвующих в пересечении ребер многогранников - видимость двух ребер пирамиды, пересекающих призму, а также видимость двух вертикальных ребер призмы, пересекающих грани пирамиды.