ЛЕКЦИЯ 7 ПОЛЯРИЗАЦИЯ СВЕТА 7 1 Поляризованный и

ЛЕКЦИЯ 7. ПОЛЯРИЗАЦИЯ СВЕТА 7. 1 Поляризованный и естественный свет. Закон Малюса

Поляризованный свет Поляризованным называется свет, в котором колебания светового вектора E каким-то образом упорядочены. В плоскополяризованном (линейно поляризованном) свете колебания светового вектора осуществляются в одной определенной плоскости, проходящей через луч. В эллиптически поляризованном по кругу свете конец вектора E описывает эллипс или окружность соответственно. Если направление распространение света и направление вращения светового вектора образуют правовинтовую систему, то поляризация называется правой эллиптической, в противном случае – левой эллиптической.

Естественный свет В естественном свете колебания светового вектора осуществляются во всевозможных направлениях, перпендикулярных к лучу; направления колебания быстро и беспорядочно сменяют друга. При решении многих задач поляризованный и естественный свет удобно представить в виде суперпозиции двух волн, поляризованных во взаимно перпендикулярных направлениях.

Плоскополяризованный свет Утверждение 1. Плоскополяризованный свет и эллиптически поляризованный свет можно представить в виде наложения (суперпозиции) двух когерентных электромагнитных волн, поляризованных во взаимно перпендикулярных плоскостях (это же относится и к свету, поляризованному по кругу, как частному случаю эллиптической поляризации).

Плоскополяризованный свет Рассмотрим в некоторой произвольной точке пространства колебания световых векторов двух плоских поляризованных во взаимно перпендикулярных плоскостях волн E 1 и E 2, распространяющихся вдоль оси Z, тогда колебания E 1 происходят вдоль оси X, а колебания E 2 – вдоль оси Y Здесь – не зависящая от времени разность фаз этих волн.

Плоскополяризованный свет Световой вектор результирующей волны – это векторная сумма E 1 и E 2: Определим вид траектории, которую описывает конец вектора E. Для этого исключим из уравнений колебаний E 1 и E 2 время t (см. Лекцию 1: сложение взаимно перпендикулярных колебаний): Т. о. , траектория конца светового вектора E – наклонный эллипс, лежащий в плоскости Z = const.

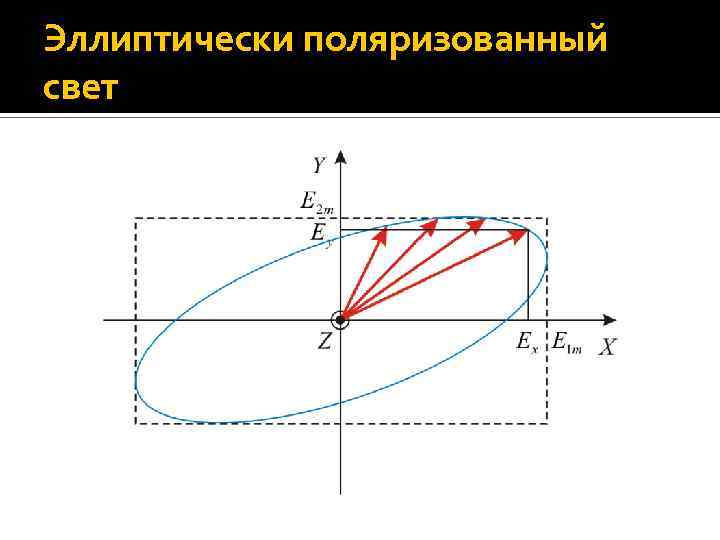Эллиптически поляризованный свет

Плоскополяризованный свет Положим = 0 или , тогда Траектория конца вектора E – прямая, т. е. при сложении двух когерентных плоскополяризованных волн с разностью фаз 0 или возникает плоскополяризованная волна. Утверждение 1 доказано.

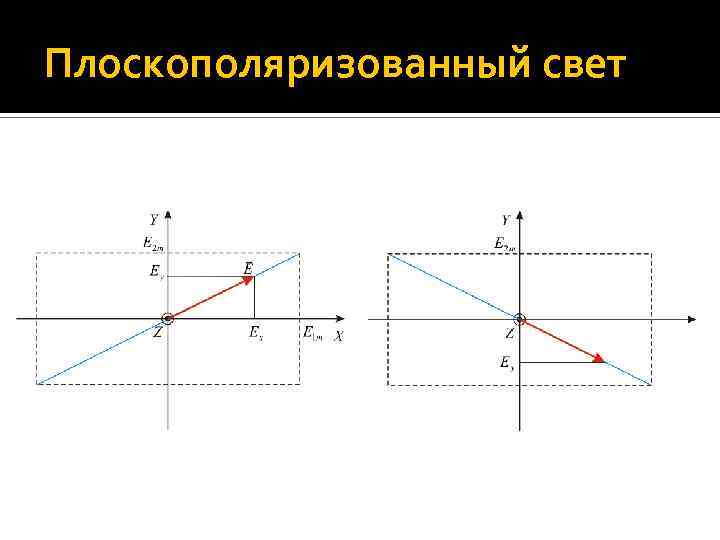Плоскополяризованный свет

Естественный свет Утверждение 2. Естественную световую волну можно представить в виде наложения (суперпозиции) двух некогерентных волн одинаковой амплитуды, поляризованных во взаимно перпендикулярных направлениях. Рассмотрим две плоские волны, световые векторы E 1 и E 2 которых параллельны осям X и Y соответственно. Тогда колебания E 1 и E 2 описываются уравнениями: Здесь (t) – разность фаз волн, хаотично изменяющаяся с течением времени.

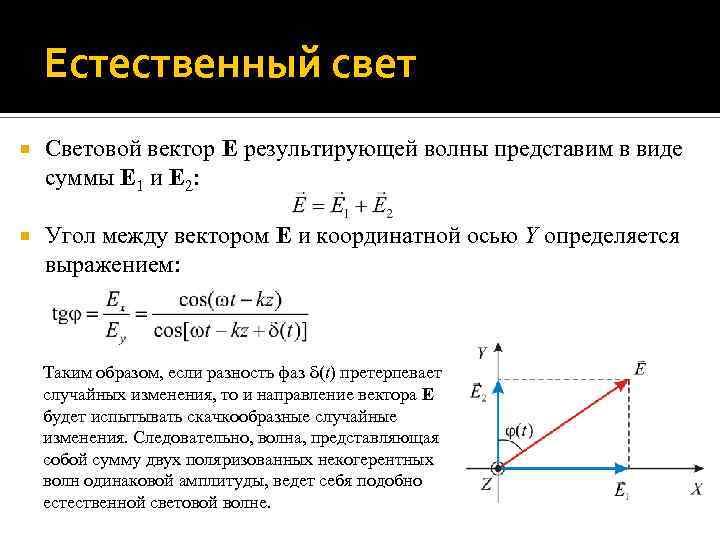Естественный свет Световой вектор E результирующей волны представим в виде суммы E 1 и E 2: Угол между вектором E и координатной осью Y определяется выражением: Таким образом, если разность фаз (t) претерпевает случайных изменения, то и направление вектора E будет испытывать скачкообразные случайные изменения. Следовательно, волна, представляющая собой сумму двух поляризованных некогерентных волн одинаковой амплитуды, ведет себя подобно естественной световой волне.

Поляризатор. Плоскость пропускания полизатора Поляризатором называется прибор, который свободно пропускает колебания светового вектора, параллельные одной определенной оси (она называется плоскостью пропускания поляризатора), и задерживает колебания, перпендикулярные к этой плоскости. Основной элемент поляризатора – прозрачная пластинка, вырезанная из кристалла с особыми свойствами, например, турмалина. Турмалин сильно поглощает световые лучи, в которых световой вектор перпендикулярен так называемой кристаллографической (оптической) оси кристалла. Если же электрический вектор параллелен этой оси, то такие лучи проходят через турмалин почти без поглощения. Естественный свет после прохождения через поляризатор становится плоскополяризованным.

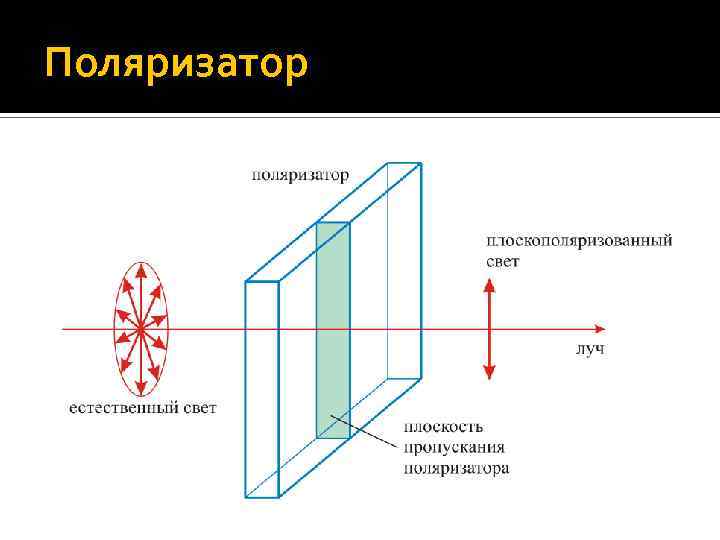Поляризатор

Частично поляризованный свет – это свет, в котором колебания светового вектора одного направления преобладают по амплитуде над колебаниями всех других направлений. Частично поляризованный свет можно рассматривать как смесь естественного и плоскополяризованного света. Проведем следующий опыт. Пусть частично поляризованный свет падает на поляризатор. Вращая прибор вокруг направления луча будем регистрировать изменение интенсивности I прошедшего через поляризатор света.

Степень поляризации Если плоскость поляризатора параллельна плоскости преобладающего колебания светового вектора частично поляризованной волны, то регистрируемая интенсивность окажется максимальной Imax. Если указанные плоскости перпендикулярны другу, интенсивность прошедшего света принимает наименьшее значение Imin

Степень поляризации Степенью поляризации частично поляризованного света называется величина, равная Здесь Imax и Imin – максимальное и минимальное значения интенсивности прошедшего через поляризатор света, регистрируемые в процессе вращения прибора вокруг направления луча.

Степень поляризации плоскополяризованного света Пример 1. Если на поляризатор падает плоскополяризованный свет, то минимальное значение интенсивность прошедшего через прибор света равно нулю, т. е. Imin = 0. Поэтому Таким образом, степень поляризации плоскополяризованного света равна единице.

Степень поляризации естественного света Пример 2. Если на поляризатор падает естественный свет, то интенсивность прошедшего света не меняется при вращении прибора. Поэтому Таким образом, степень поляризации естественного света равна нулю.

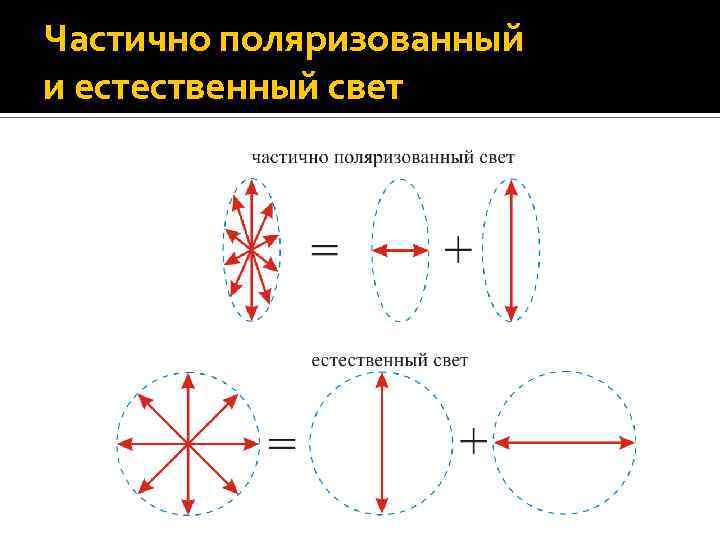Частично поляризованный и естественный свет

Закон Малюса Если на поляризатор падает плоскополяризованный свет интенсивности I 0, то интенсивность I прошедшего через поляризатор света связана с I 0 соотношением: Здесь – угол между плоскостью колебаний светового вектора в падающей волне и плоскостью пропускания поляризатора (т. е. плоскостью колебания светового вектора в прошедшей волне). Данное соотношение называется законом Малюса. Приведем его обоснование.

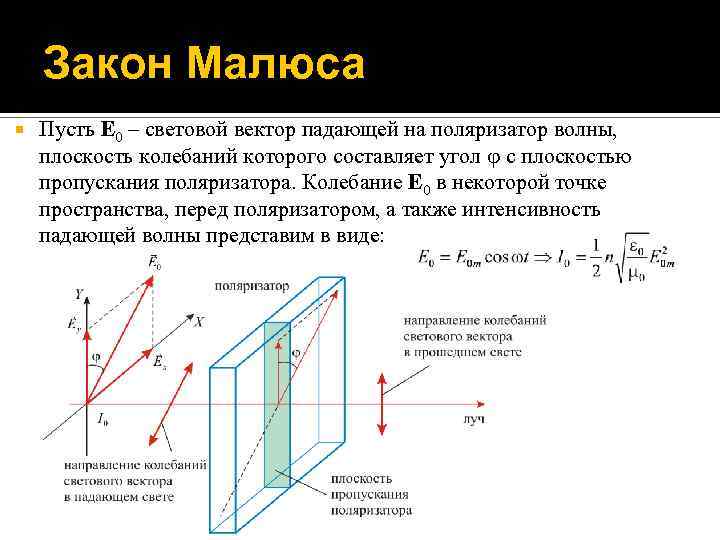Закон Малюса Пусть E 0 – световой вектор падающей на поляризатор волны, плоскость колебаний которого составляет угол с плоскостью пропускания поляризатора. Колебание E 0 в некоторой точке пространства, перед поляризатором, а также интенсивность падающей волны представим в виде:

Закон Малюса Направим оси координат Y и X соответственно параллельно и перпендикулярно плоскости пропускания поляризатора и разложим E 0 на составляющие вдоль этих осей: E 0 = Ex + Ey. Тогда колебания векторов Ex и Ey имеют вид:

Закон Малюса Составляющая Ex будет задержана поляризатором, а составляющая Ey, параллельная плоскости поляризатора, свободно пройдет через поляризатор. Интенсивность прошедшего света:

Прохождение естественного света через поляризатор Если на поляризатор падает естественный свет интенсивности I 0, то интенсивность прошедшей волны вдвое меньше интенсивности падающего света: Докажем это. Как известно, световой вектор E 0 падающей на поляризатор световой волны можно разложить на две некогерентные составляющие одинаковой амплитуды. Здесь E||, E - соответственно составляющие, параллельная и перпендикулярная плоскости пропускания поляризатора

Прохождение естественного света через поляризатор Колебания векторов E||, E задаются уравнениями: Здесь (t) – разность фаз этих составляющих, претерпевающая хаотические изменения. Амплитуды составляющих и, следовательно, интенсивности, одинаковы: I|| = I ; при этом, поскольку волны не когерентны, то I|| + I = I 0. Таким образом, находим: I|| = I = 0, 5 I 0. Поскольку поляризатор задерживает составляющую E и пропускает составляющую E||, то интенсивность прошедшей волны I = I|| = 0, 5 I 0.

ЛЕКЦИЯ 7. ПОЛЯРИЗАЦИЯ СВЕТА 7. 2 Поляризация при отражении и преломлении

Поляризация при отражении и преломлении Пусть естественная световая волна падает на границу раздела двух диэлектриков с абсолютными показателями преломления n 1 и n 2. Обозначим: i и r – соответственно угол падения (отражения) и преломления.

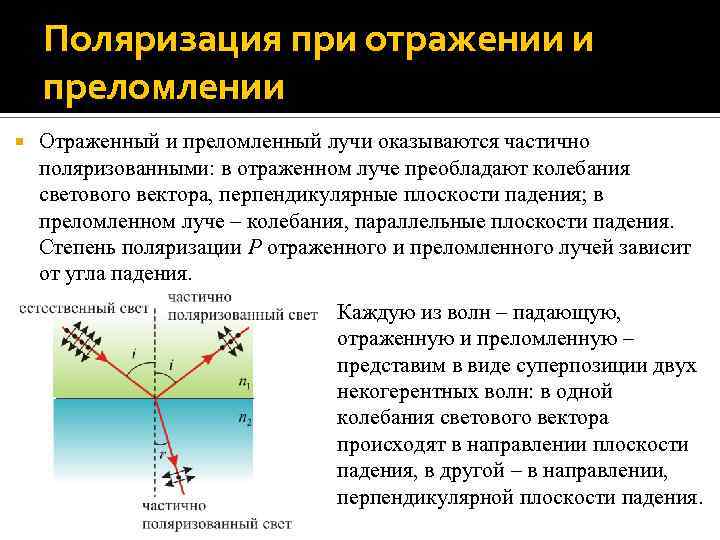Поляризация при отражении и преломлении Отраженный и преломленный лучи оказываются частично поляризованными: в отраженном луче преобладают колебания светового вектора, перпендикулярные плоскости падения; в преломленном луче – колебания, параллельные плоскости падения. Степень поляризации P отраженного и преломленного лучей зависит от угла падения. Каждую из волн – падающую, отраженную и преломленную – представим в виде суперпозиции двух некогерентных волн: в одной колебания светового вектора происходят в направлении плоскости падения, в другой – в направлении, перпендикулярной плоскости падения.

Поляризация при отражении и преломлении Обозначим: I|| и I - интенсивности этих составляющих в падающей волне, I || и I - в отраженной волне, I || и I - в преломленной волне.

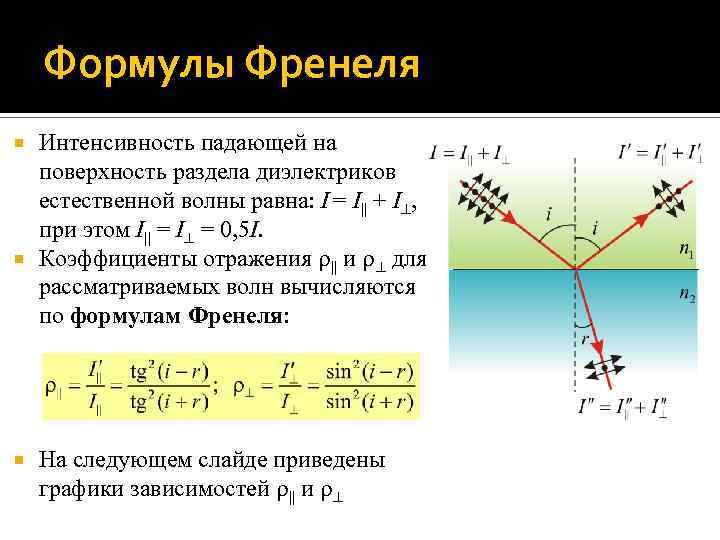Формулы Френеля Интенсивность падающей на поверхность раздела диэлектриков естественной волны равна: I = I|| + I , при этом I|| = I = 0, 5 I. Коэффициенты отражения || и для рассматриваемых волн вычисляются по формулам Френеля: На следующем слайде приведены графики зависимостей || и

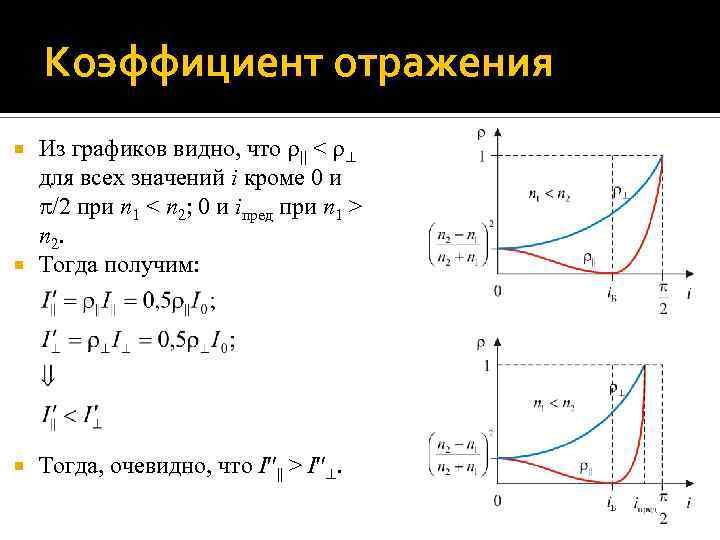Коэффициент отражения Из графиков видно, что || < для всех значений i кроме 0 и /2 при n 1 < n 2; 0 и iпред при n 1 > n 2. Тогда получим: Тогда, очевидно, что I || > I .

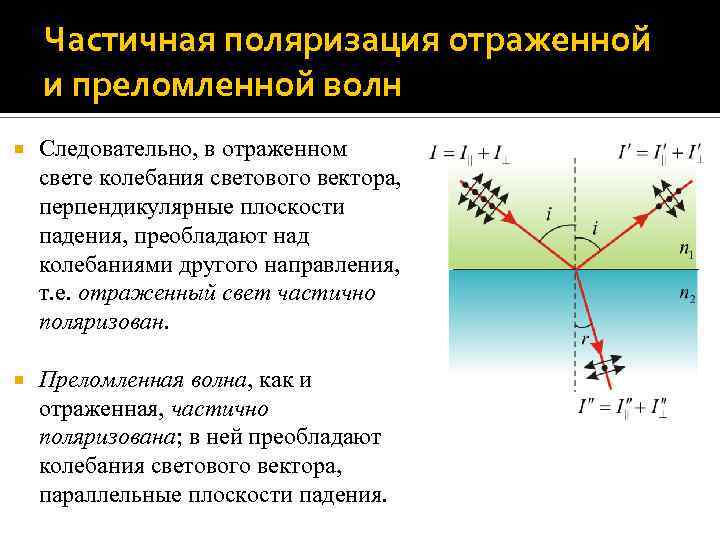Частичная поляризация отраженной и преломленной волн Следовательно, в отраженном свете колебания светового вектора, перпендикулярные плоскости падения, преобладают над колебаниями другого направления, т. е. отраженный свет частично поляризован. Преломленная волна, как и отраженная, частично поляризована; в ней преобладают колебания светового вектора, параллельные плоскости падения.

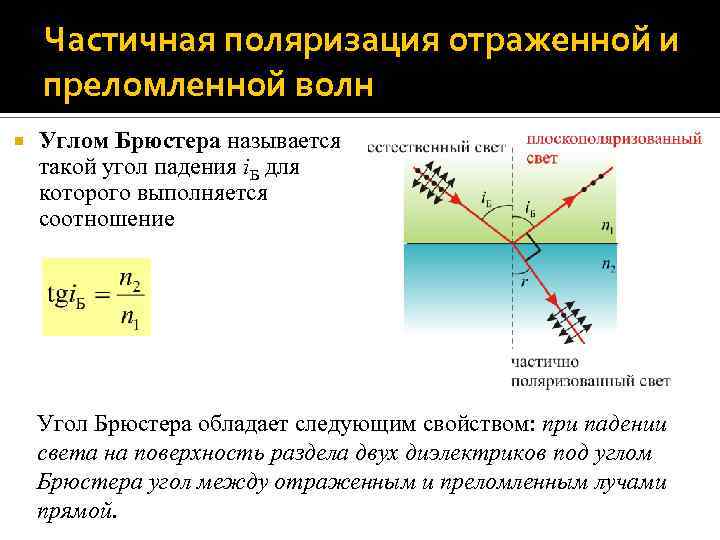Частичная поляризация отраженной и преломленной волн Углом Брюстера называется такой угол падения i. Б для которого выполняется соотношение Угол Брюстера обладает следующим свойством: при падении света на поверхность раздела двух диэлектриков под углом Брюстера угол между отраженным и преломленным лучами прямой.

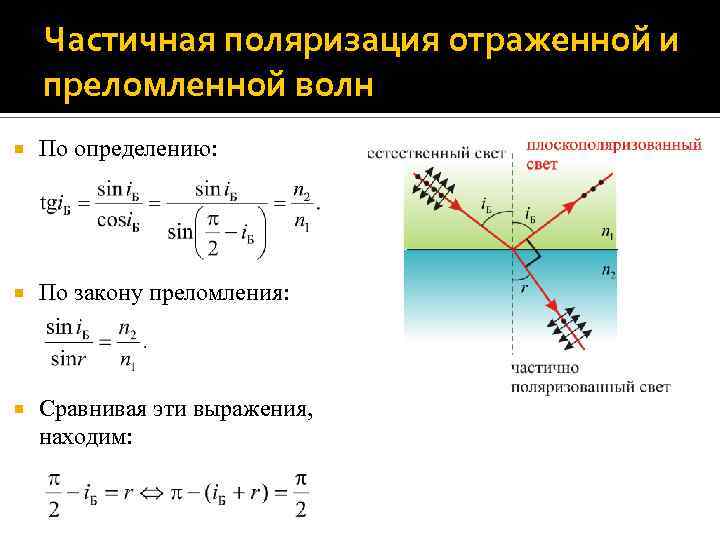Частичная поляризация отраженной и преломленной волн По определению: По закону преломления: Сравнивая эти выражения, находим:

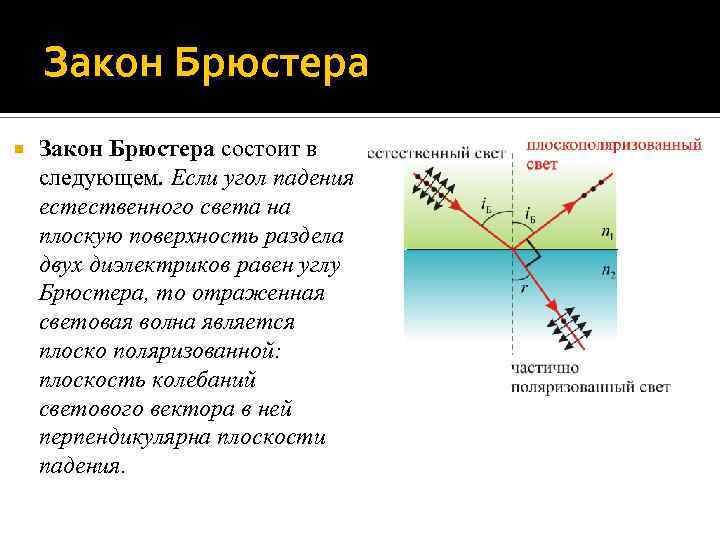Закон Брюстера состоит в следующем. Если угол падения естественного света на плоскую поверхность раздела двух диэлектриков равен углу Брюстера, то отраженная световая волна является плоско поляризованной: плоскость колебаний светового вектора в ней перпендикулярна плоскости падения.

Закон Брюстера Таким образом, если i = i. Б, то i. Б + r = /2 и коэффициент отражения: Тогда отраженная волна полностью поляризована, в ней колебания светового вектора перпендикулярны к плоскости падения.

ЛЕКЦИЯ 7. ПОЛЯРИЗАЦИЯ СВЕТА 7. 3 Двойное лучепреломление

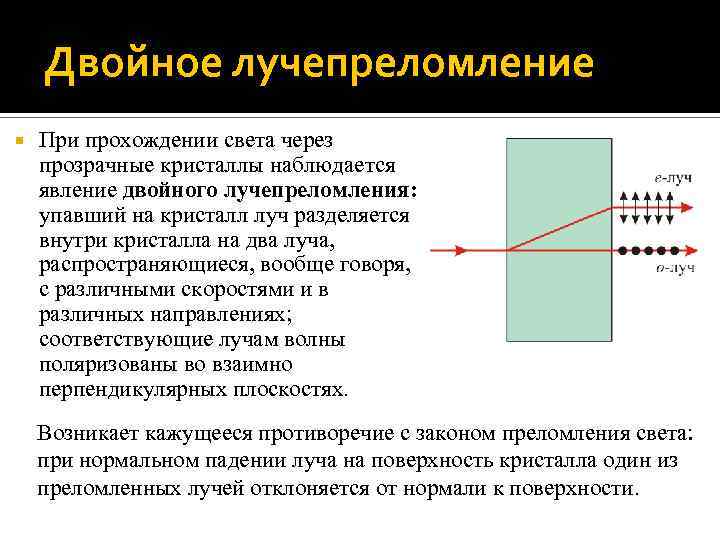Двойное лучепреломление При прохождении света через прозрачные кристаллы наблюдается явление двойного лучепреломления: упавший на кристалл луч разделяется внутри кристалла на два луча, распространяющиеся, вообще говоря, с различными скоростями и в различных направлениях; соответствующие лучам волны поляризованы во взаимно перпендикулярных плоскостях. Возникает кажущееся противоречие с законом преломления света: при нормальном падении луча на поверхность кристалла один из преломленных лучей отклоняется от нормали к поверхности.

Изотропные кристаллы Двойное лучепреломление объясняется анизотропией кристаллов. Для находящегося в электрическом поле с напряженностью E изотропного кристалла связь между поляризованностью P, электрической индукцией и напряженностью E устанавливается соотношениями: Здесь – диэлектрическая восприимчивость, = + 1 – диэлектрическая проницаемость вещества. Данные соотношения выполняются при произвольной ориентации вектора E в кристалле, причем P и D E.

Анизотропные кристаллы В анизотропных кристаллах, помещенных в электрическое поле, векторы P и D, вообще говоря, не коллинеарны с E. Связь между D и E следующая: Здесь элементами матрицы 3 3 являются компоненты ij так называемого тензора диэлектрической проницаемости.

Главные направления анизотропного кристалла Всегда можно выбрать оси X, Y и Z декартовой системы координат таким образом, что матрица станет диагональной: Такие направления координатных осей X, Y и Z в кристалле, для которых матрица тензора диэлектрической проницаемости является диагональной, называются главными направлениями.

Двойное лучепреломление Если вектор E совпадает с одним из главных направлений, то D E. Если, например, E = Ei, то D = 0 x. E X. Если, например, E = Ej, то D = 0 y. E Y. Если же E = Ek, то D = 0 z. E Z. Трем компонентам x, y, z диагонального тензора диэлектрической проницаемости соответствуют три различных показателя преломления: Фазовые скорости волн, в которых световой вектор E параллелен осям X, Y и Z соответственно: vx, y, z = c/nx, y, z.

Одно- и двуосные кристаллы. Главная оптическая ось кристалла Кристаллы, для которых все три диагональных элемента x, y, z тензора диэлектрической проницаемости различны, называются двуосными (слюда, гипс). Кристаллы, для которых nx = ny, но nx nz, называются одноосными (кварц, ирландский шпат, турмалин). В одноосных кристаллах ось Z, которой соответствует отличный от двух других одинаковых главных показателей преломления nx и ny главный показатель преломления nz называется оптической осью кристалла.

Положительные и отрицательные кристаллы Главный показатель преломления nz обозначается символом ne. Таким образом, ne – показатель преломления для распространяющихся в кристалле волн, у которых колебания светового вектора E происходят параллельно оптической оси. Два других одинаковых главных показателя преломления nx = ny обозначают символом no. Итак, no – показатель преломления для волн в кристалле, у которых колебания светового вектора E происходят в перпендикулярном к оптической оси направлении. Положительными называют кристаллы, у которых ne > no, отрицательными – кристаллы, у которых ne < no.

Главное сечение кристалла. Обыкновенный и необыкновенный лучи Главной плоскостью (главным сечением) кристалла называется плоскость, в которой лежит оптическая ось. Очевидно, что главных сечений бесконечно много, поэтому часто главным сечением называют плоскость, в которой лежат оптическая ось и световой луч. Если вектор E световой волны принадлежит главному сечению, волна называется необыкновенной, соответствующий луч также называется необыкновенным и обозначается буквой e; волна, у которой колебания вектора E происходят в направлении, перпендикулярном главному сечению, называется обыкновенной, которой соответствует так называемый обыкновенный луч, обозначаемый буквой o.

Двойное лучепреломление Пусть в точке O внутри кристалла находится точечный источник естественного света; через точку O проходит ось кристалла – ось Z, и при этом плоскость чертежа является одним из главных сечений. В любом выходящем из точки O луче естественного света колебания вектора E происходят во всевозможных направлениях, перпендикулярных лучу. Всякий выходящий из точки O луч можно рассматривать как суперпозицию двух совпадающих по направлению распространения лучей – обыкновенного и необыкновенного.

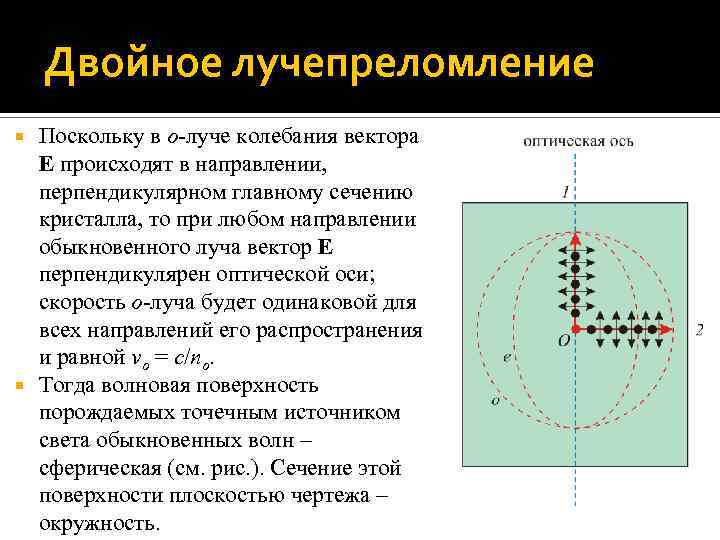Двойное лучепреломление Поскольку в о-луче колебания вектора E происходят в направлении, перпендикулярном главному сечению кристалла, то при любом направлении обыкновенного луча вектор E перпендикулярен оптической оси; скорость о-луча будет одинаковой для всех направлений его распространения и равной vo = c/no. Тогда волновая поверхность порождаемых точечным источником света обыкновенных волн – сферическая (см. рис. ). Сечение этой поверхности плоскостью чертежа – окружность.

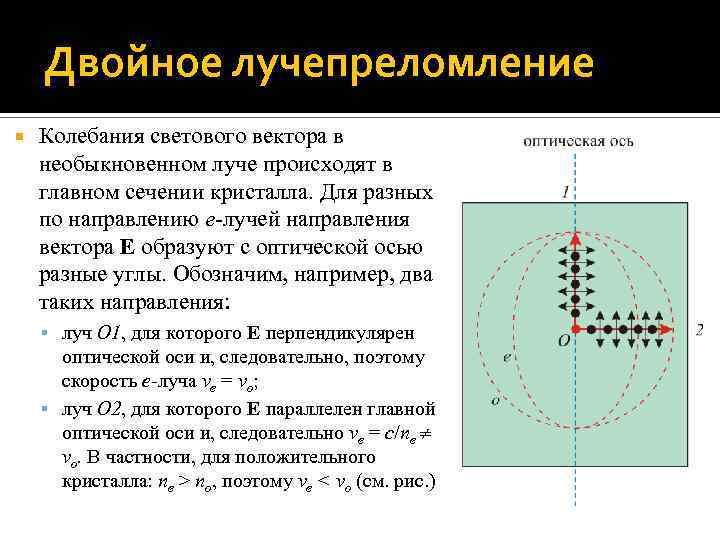Двойное лучепреломление Колебания светового вектора в необыкновенном луче происходят в главном сечении кристалла. Для разных по направлению e-лучей направления вектора E образуют с оптической осью разные углы. Обозначим, например, два таких направления: луч O 1, для которого E перпендикулярен оптической оси и, следовательно, поэтому скорость e-луча ve = vo; луч O 2, для которого E параллелен главной оптической оси и, следовательно ve = c/ne vo. В частности, для положительного кристалла: ne > no, поэтому ve < vo (см. рис. )

Двойное лучепреломление Для всех других лучей, кроме O 1 и O 2, фазовые скорости имеют промежуточные значения между vo и ve. Если изобразить множество точек, до которых дошла необыкновенная волна к определенному моменту времени, то полученная волновая поверхность представляет собой эллипсоид вращения. Сечение этого эллипсоида плоскостью чертежа – эллипс.

Примеры двойного лучепреломления Пример 1. Пусть на поверхность кристалла нормально падает естественная световая волна; оптическая ось кристалла лежит в плоскости чертежа, образуя угол с преломляющей поверхностью кристалла; таким образом, плоскость чертежа – главное сечение кристалла. Падающий на кристалл луч представим как совокупность двух волн, поляризованных в двух взаимно перпендикулярных плоскостях.

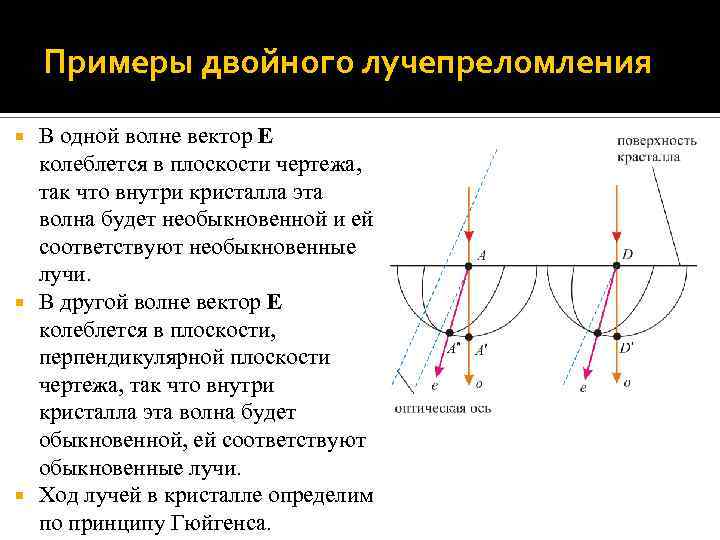Примеры двойного лучепреломления В одной волне вектор E колеблется в плоскости чертежа, так что внутри кристалла эта волна будет необыкновенной и ей соответствуют необыкновенные лучи. В другой волне вектор E колеблется в плоскости, перпендикулярной плоскости чертежа, так что внутри кристалла эта волна будет обыкновенной, ей соответствуют обыкновенные лучи. Ход лучей в кристалле определим по принципу Гюйгенса.

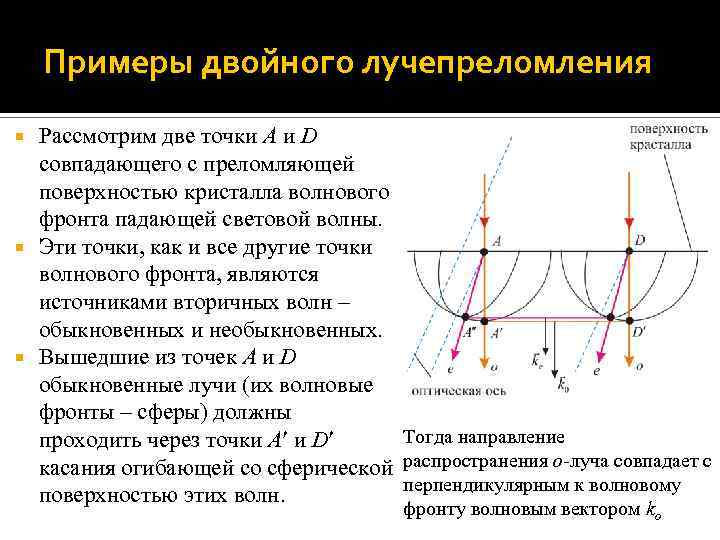Примеры двойного лучепреломления Рассмотрим две точки A и D совпадающего с преломляющей поверхностью кристалла волнового фронта падающей световой волны. Эти точки, как и все другие точки волнового фронта, являются источниками вторичных волн – обыкновенных и необыкновенных. Вышедшие из точек A и D обыкновенные лучи (их волновые фронты – сферы) должны Тогда направление проходить через точки A и D касания огибающей со сферической распространения о-луча совпадает с перпендикулярным к волновому поверхностью этих волн. фронту волновым вектором ko

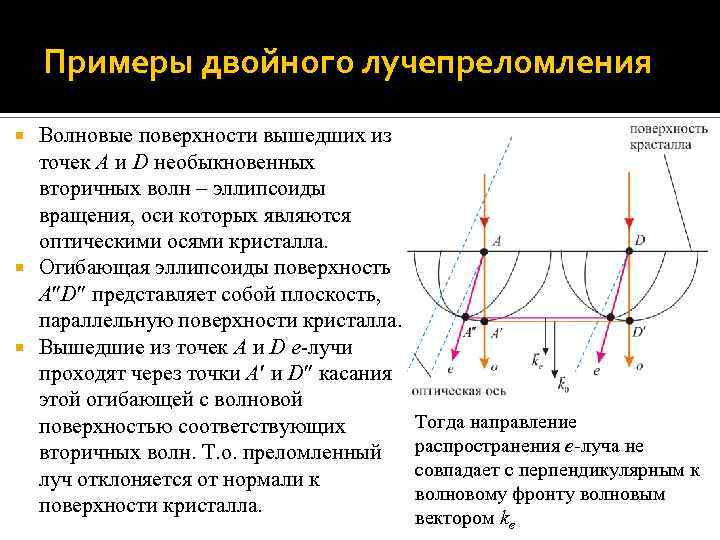Примеры двойного лучепреломления Волновые поверхности вышедших из точек A и D необыкновенных вторичных волн – эллипсоиды вращения, оси которых являются оптическими осями кристалла. Огибающая эллипсоиды поверхность A D представляет собой плоскость, параллельную поверхности кристалла. Вышедшие из точек A и D e-лучи проходят через точки A и D касания этой огибающей с волновой поверхностью соответствующих вторичных волн. Т. о. преломленный луч отклоняется от нормали к поверхности кристалла. Тогда направление распространения e-луча не совпадает с перпендикулярным к волновому фронту волновым вектором ke

Примеры двойного лучепреломления Напомним, что лучами называются линии, вдоль которых распространяется энергия световой волны. Как видно из рассмотренного примера с необыкновенным лучом, направление переноса энергии (направление необыкновенного луча) не обязательно совпадает с направлением вектора ke необыкновенной волны, который всегда перпединкулярен волновой поверхности

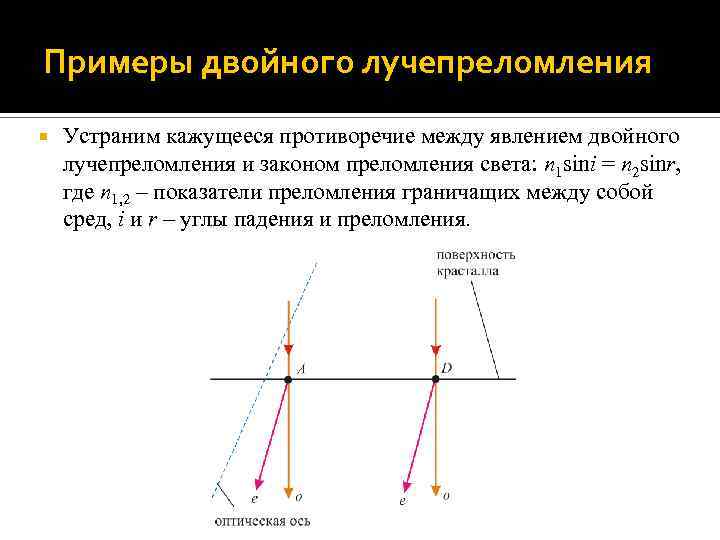Примеры двойного лучепреломления Устраним кажущееся противоречие между явлением двойного лучепреломления и законом преломления света: n 1 sini = n 2 sinr, где n 1, 2 – показатели преломления граничащих между собой сред, i и r – углы падения и преломления.

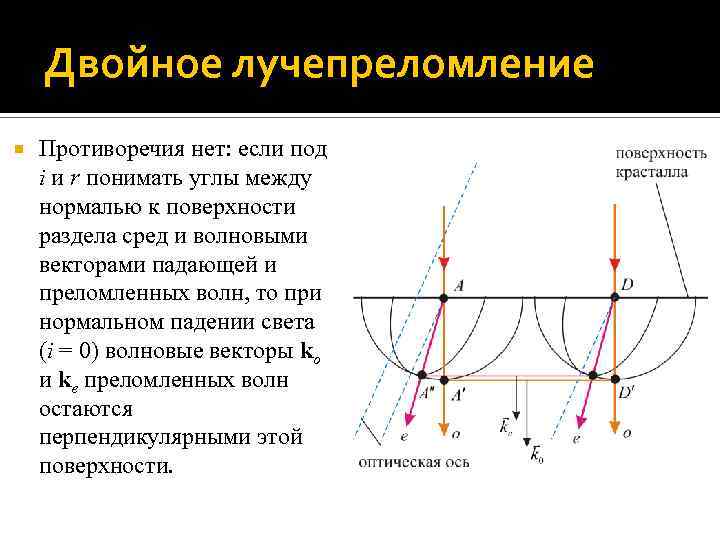Двойное лучепреломление Противоречия нет: если под i и r понимать углы между нормалью к поверхности раздела сред и волновыми векторами падающей и преломленных волн, то при нормальном падении света (i = 0) волновые векторы ko и ke преломленных волн остаются перпендикулярными этой поверхности.

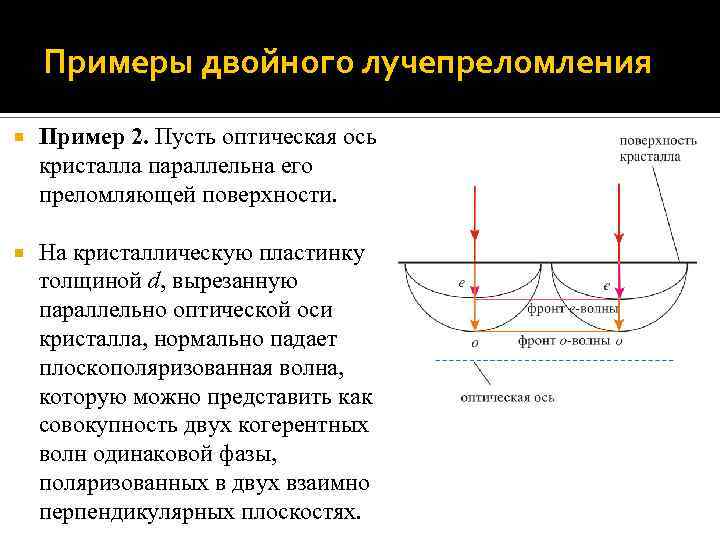Примеры двойного лучепреломления Пример 2. Пусть оптическая ось кристалла параллельна его преломляющей поверхности. На кристаллическую пластинку толщиной d, вырезанную параллельно оптической оси кристалла, нормально падает плоскополяризованная волна, которую можно представить как совокупность двух когерентных волн одинаковой фазы, поляризованных в двух взаимно перпендикулярных плоскостях.

Примеры двойного лучепреломления Т. о. , направление колебаний светового вектора одной из волн лежит в плоскости чертежа и принадлежит главному сечению кристалла; этой волне соответствует e-луч. В другой волне направление колебаний светового вектора перпендикулярно плоскости чертежа; этой волне соответствует распространяющийся в кристалле o-луч. Оба луча распространяются по одному и тому же направлению, но с разными скоростями

Примеры двойного лучепреломления Если бы в момент падения на поверхность кристалла поляризованные в двух взаимно перпендикулярных плоскостях волны обладали одинаковой фазой, то при выходе из пластинки между ними возникнет разность фаз В частности, если = /2, то на выходе из пластинки кристалла поучается эллиптический поляризованный свет; если = , то выходящий из кристалла свет остается плоскополяризованным, но положение плоскости поляризации меняется.

Примеры двойного лучепреломления Вырезанная параллельно оптической оси кристалла пластинка, для которой выполняется условие или иначе называется пластинкой в четверть волны. С помощью такой пластинки из падающего на кристалл плоскополяризованного света получается эллиптически поляризованный свет.

Примеры двойного лучепреломления Вырезанная параллельно оптической оси кристалла пластинка, для которой выполняется условие или иначе называется пластинкой в полволны. В результате прохождения плоскополяризованного света через такую пластинку свет остается плоскополяризованным, но положение плоскости поляризации изменяется.

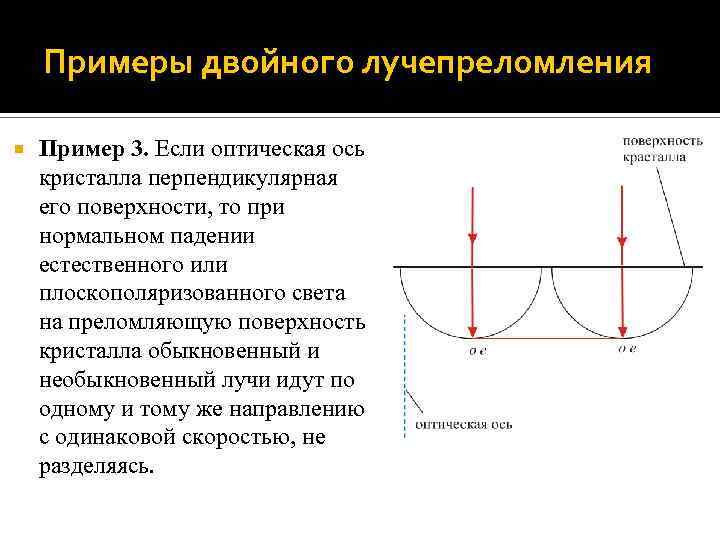Примеры двойного лучепреломления Пример 3. Если оптическая ось кристалла перпендикулярная его поверхности, то при нормальном падении естественного или плоскополяризованного света на преломляющую поверхность кристалла обыкновенный и необыкновенный лучи идут по одному и тому же направлению с одинаковой скоростью, не разделяясь.

ЛЕКЦИЯ 7. ПОЛЯРИЗАЦИЯ СВЕТА 7. 4 Искусственная оптическая анизотропия

Искусственная оптическая анизотропия Естественная оптическая анизотропия для ряда кристаллов связана с пространственной и ориентационной упорядоченностью их атомов, молекул или ионов, т. е. анизотропией среды. В общем случае такая упорядоченность отсутствует у аморфных тел и жидкостей (за исключение жидких кристаллов). Поэтому эти вещества являются оптически изотропными, т. е. их оптические свойства одинаковы по всем направлениям.

Искусственная оптическая анизотропия Оказывается, что оптические изотропные вещества приобретают анизотропные свойства под действием: одностороннего сжатия (или растяжения); электрического или магнитного полей В этом случае вещество приобретает свойства одноосных кристаллов, оптическая ось которых совпадает с направлением деформации, электрического или магнитного полей.

Искусственная оптическая анизотропия при деформациях Мерой возникающей оптической анизотропии служит разность показателей преломления обыкновенного no и необыкновенного ne лучей, распространяющихся в направлении, перпендикулярном к оптической оси. При механических воздействиях где k 1 – коэффициент, характеризующий вещество; – механическое напряжение.

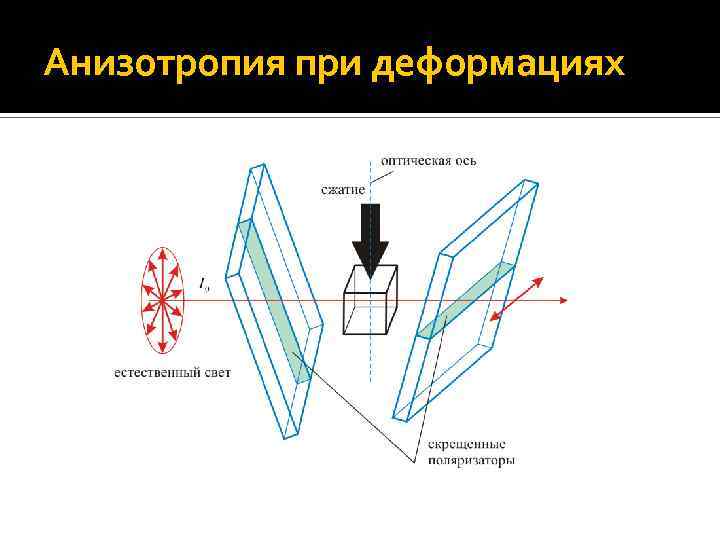
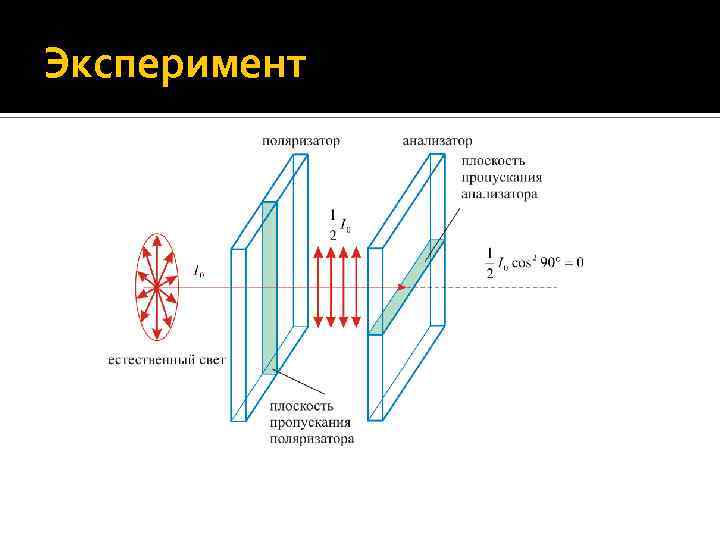
Искусственная оптическая анизотропия при деформациях Явление оптической анизотропии при деформации вещества широко используемся для изучения распределения напряжений в моделях сооружений и устройств. Пусть плоскости пропускания поляризатора и анализатора взаимно перпендикулярны (см. следующий слайд), поэтому при отсутствии механических сил свет через систему не проходит. Интенсивность прошедшего света зависит от разности no – ne, а значит, от механического напряжения.

Анизотропия при деформациях

Эффект Керра Оптическая анизотропия, возникающая под действием электрического поля, зависит от напряженности E этого поля. Это явление было открыто в 1875 г. английским физиком Д. Керром и называется эффектом Керра. Мера анизотропии в этом случае определяется соотношением где k 2 – коэффициент, характеризующий вещество, E – модуль напряженности приложенного электрического поля

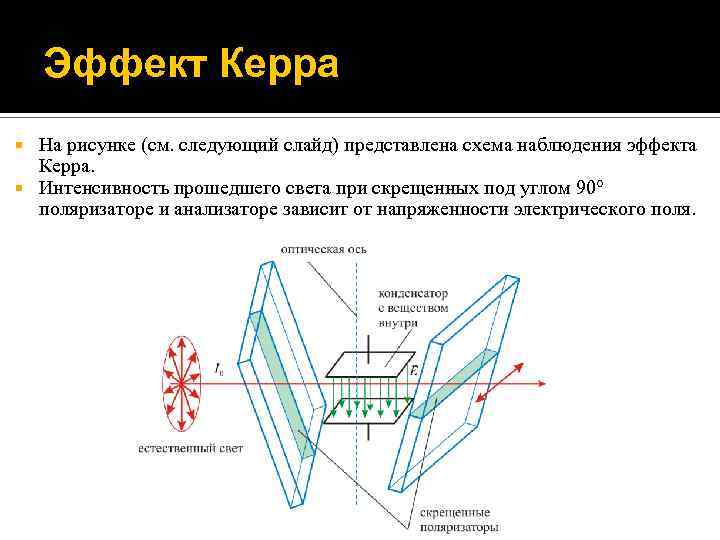Эффект Керра На рисунке (см. следующий слайд) представлена схема наблюдения эффекта Керра. Интенсивность прошедшего света при скрещенных под углом 90 поляризаторе и анализаторе зависит от напряженности электрического поля.

Эффект Керра находит широкое применение. Возникновение и исчезновение оптической анизотропии при включении/выключении внешнего электрического поля практически безынерционно (составляет примерно 10 -10 с). Поэтому ячейка Керра используется как хороший световой затвор и применяется в быстро протекающих процессах (запись и воспроизведение звука, скоростная фото- и киносъемка, оптическая телефония и т. д. )

Эффект Коттона – Муттона Оптическая анизотропия, возникающая под действием магнитного поля (эффект Коттона - Муттона), описывается соотношением Здесь k 3 – коэффициент, характеризующий вещество, H – напряженность приложенного магнитного поля. Исследование эффектов, связанных с искусственной анизотропией среды, позволяет получить информацию о структуре и ориентационной подвижности молекул в веществе.

Лазерная искусственная оптическая анизотропия В заключение отметим возникновение оптической анизотропии под действием мощного светового (лазерного) потока. Электрическое поле световой поляризованной волны также способно поляризовать молекулы или атомы вещества и обусловливать оптическую анизотропию среды. Большие успехи в применении этого метода для изучения быстро протекающих процессов в жидкостях достигнуты благодаря использованию пикосекундных и фемтосекундных лазерных потоков (длительность светового импульса 10 -12 – 10 -15 с).

ЛЕКЦИЯ 7. ПОЛЯРИЗАЦИЯ СВЕТА 7. 5 Вращение плоскости поляризации

Вращение плоскости поляризации Если плоскополяризованный свет проходит через плоскопараллельный слой вещества, то в некоторых случаях плоскость поляризации света оказывается повернутой относительно своего исходного положения. Это явление называется вращением плоскости поляризации или оптической активностью. Если вещество при этом не находится во внешнем магнитном поле, то оптическая активность и вращение плоскости поляризации называются естественными. В противном случае говорят о магнитном вращении плоскости поляризации или эффекте Фарадея.

Оптически активные вещества. Угол поворота плоскости поляризации в кристаллах К числу оптически активных веществ принадлежат кристаллические тела (кварц), чистые жидкости (никотин, скипидар), растворы оптически активных веществ в неактивных растворителях (водный раствор сахара). Экспериментально установлено, что угол поворота плоскости поляризации пропорционален пути l, пройденному лучом в кристалле: где коэффициент называется постоянной вращения и зависит от материала вещества и длины волны света.

Угол поворота плоскости поляризации в растворах В растворах угол поворота плоскости поляризации пропорционален пути l луча в растворе и концентрации C растворенного оптически активного вещества: где уд – удельная постоянная вращения, зависящая от рода вещества и длины волны света. Если луч, прошедший через оптически активный кристалл вдоль оптической оси, отразить зеркалом и заставить пройти через кристалл еще раз в обратном направлении, то первоначальное положение плоскости поляризации восстанавливается.

Эксперимент

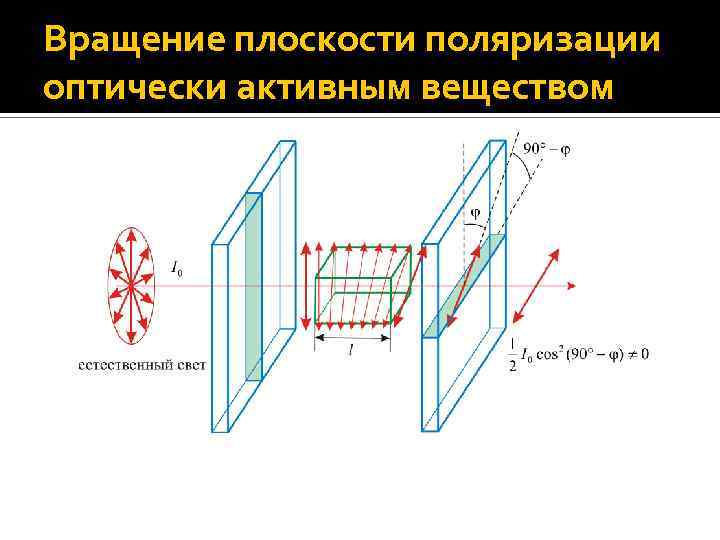Вращение плоскости поляризации оптически активным веществом

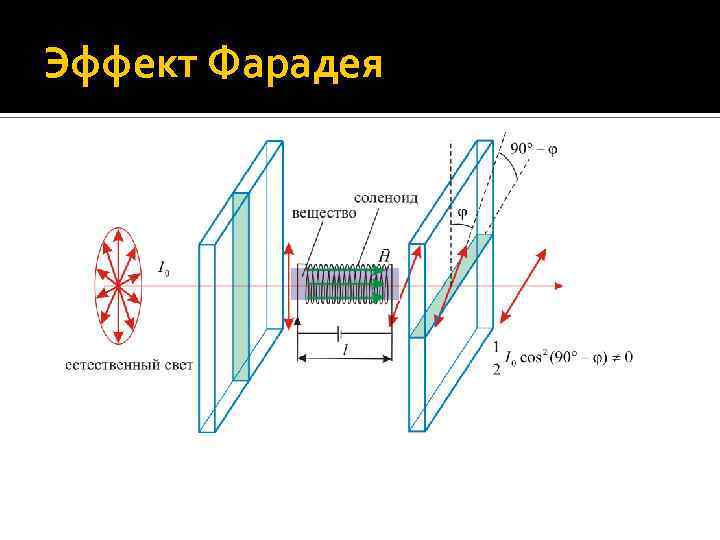
Угол поворота плоскости поляризации в растворах Оптические неактивные вещества приобретают способность вращать плоскость поляризации под действием магнитного поля (эффект Фарадея). Этот эффект наблюдается только при распространении света вдоль направления внешнего магнитного поля. Угол поворота плоскости поляризации пропорционален пути l, пройденному светом в веществе, и напряженности H магнитного поля: Здесь V – коэффициент, называемый постоянной Верде. На следующем слйде приведена схема наблюдения эффекта Фарадея

Эффект Фарадея

Угол поворота плоскости поляризации в растворах Если, отразив луч зеркалом, заставить его пройти через намагниченное вещество еще раз в обратном направлении, величина поворота плоскости поляризации удвоится. Постоянная Верде зависит от длины волны света.