Лекция 7 Пересечение поверхностей Метод секущих

Лекция 7 • Пересечение поверхностей. • Метод секущих плоскостей уровня. • Метод концентрических сфер. • Метод эксцентрических сфер.

Пересечение поверхностей Чтобы построить линию пересечения поверхностей, необходимо рассечь заданные поверхности вспомогательной поверхностью (плоскостью).

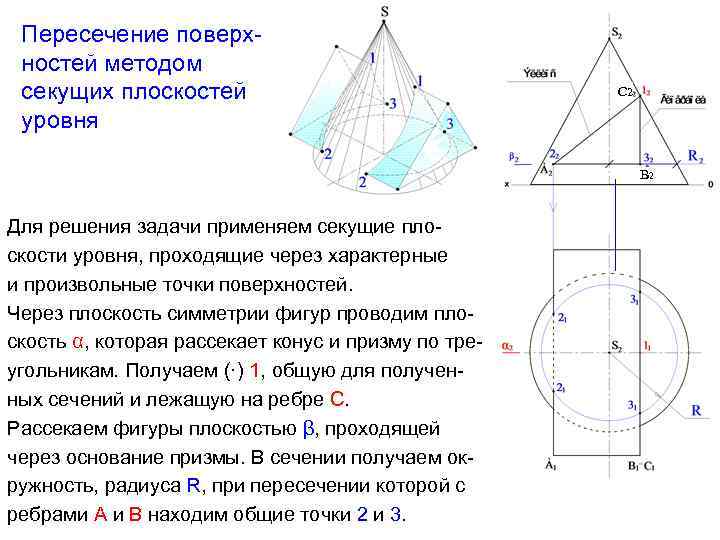Пересечение поверхностей методом секущих плоскостей уровня С 2 В 2 Для решения задачи применяем секущие плоскости уровня, проходящие через характерные и произвольные точки поверхностей. Через плоскость симметрии фигур проводим плоскость α, которая рассекает конус и призму по треугольникам. Получаем (·) 1, общую для полученных сечений и лежащую на ребре С. Рассекаем фигуры плоскостью β, проходящей через основание призмы. В сечении получаем окружность, радиуса R, при пересечении которой с ребрами А и В находим общие точки 2 и 3.

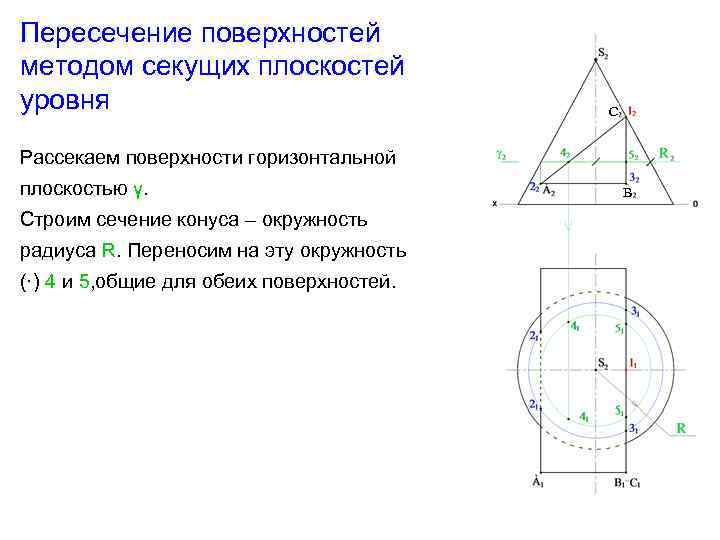Пересечение поверхностей методом секущих плоскостей уровня С Рассекаем поверхности горизонтальной плоскостью γ. Строим сечение конуса – окружность радиуса R. Переносим на эту окружность (·) 4 и 5, общие для обеих поверхностей. В

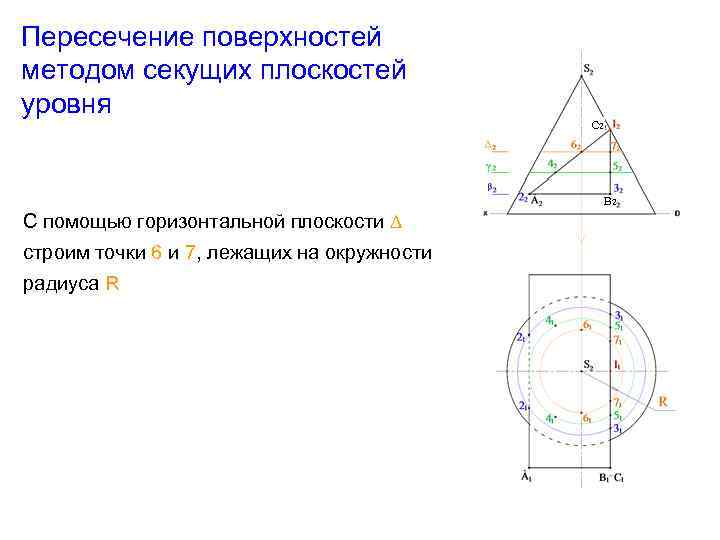Пересечение поверхностей методом секущих плоскостей уровня C 2 В 2 С помощью горизонтальной плоскости ∆ строим точки 6 и 7, лежащих на окружности радиуса R

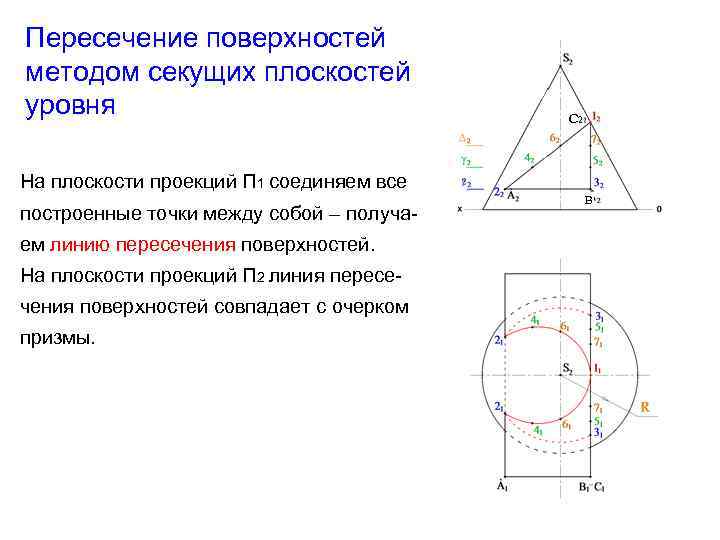Пересечение поверхностей методом секущих плоскостей уровня С 2 На плоскости проекций П 1 соединяем все построенные точки между собой – получаем линию пересечения поверхностей. На плоскости проекций П 2 линия пересечения поверхностей совпадает с очерком призмы. В

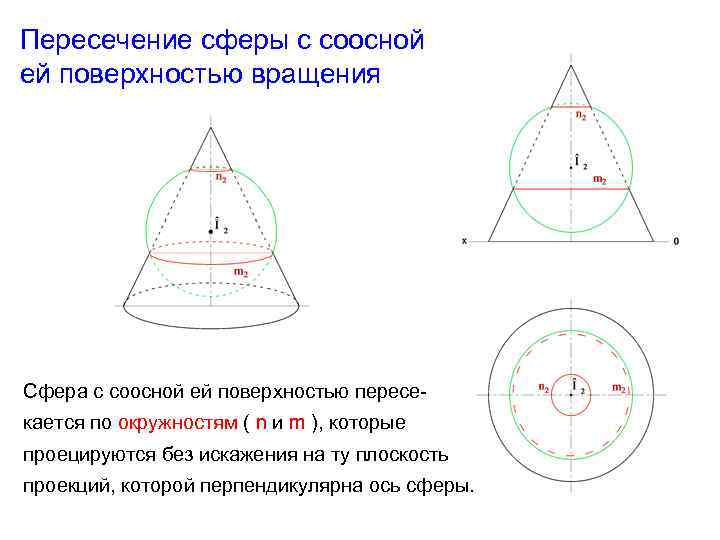Пересечение сферы с соосной ей поверхностью вращения Сфера с соосной ей поверхностью пересекается по окружностям ( n и m ), которые проецируются без искажения на ту плоскость проекций, которой перпендикулярна ось сферы.

Пересечение поверхностей вращения методом концентрических сфер Метод концентрических сфер применяется в том случае, когда: 1. Пересекаются две поверхности вращения. 2. Поверхности имеют общую плоскость симметрии. 3. Оси поверхностей пересекаются и параллельны одной из плоскостей проекций. 4. Одна из осей перпендикулярна другой плоскости проекций.

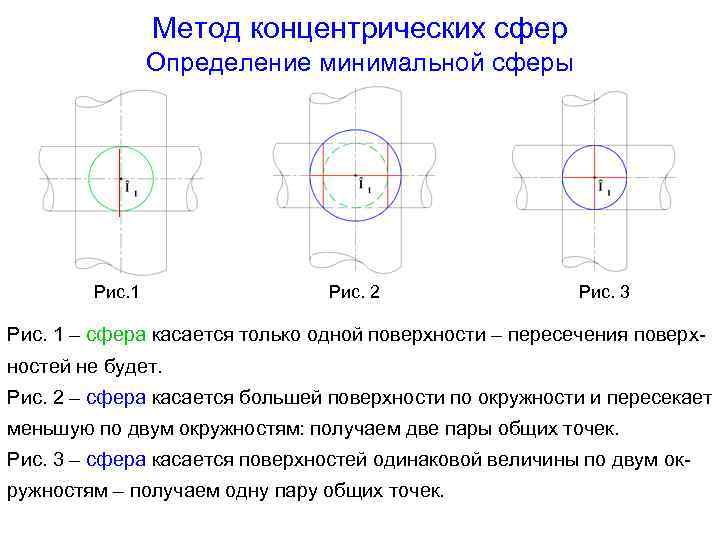Метод концентрических сфер Определение минимальной сферы Рис. 1 Рис. 2 Рис. 3 Рис. 1 – сфера касается только одной поверхности – пересечения поверхностей не будет. Рис. 2 – сфера касается большей поверхности по окружности и пересекает меньшую по двум окружностям: получаем две пары общих точек. Рис. 3 – сфера касается поверхностей одинаковой величины по двум окружностям – получаем одну пару общих точек.

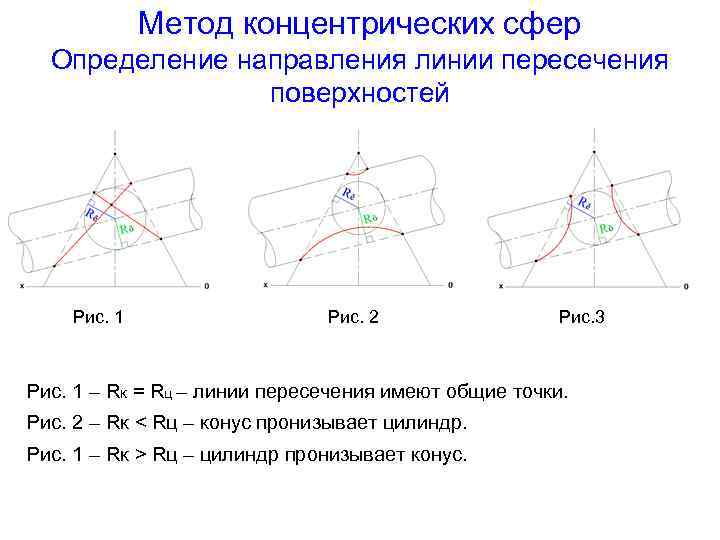Метод концентрических сфер Определение направления линии пересечения поверхностей Рис. 1 Рис. 2 Рис. 3 Рис. 1 – Rк = Rц – линии пересечения имеют общие точки. Рис. 2 – Rк < Rц – конус пронизывает цилиндр. Рис. 1 – Rк > Rц – цилиндр пронизывает конус.

Пересечение поверхностей вращения методом концентрических сфер Рассекаем поверхности плоскостью α, проходящей по плоскости симметрии поверхностей. При пересечении очерков поверхностей получаем (·) 1 и 2. Определяем радиус минимальной сферы. Это сфера, вписанная в конус. Определяем радиус максимальной сферы. Это сфера, проходящая через наиболее удаленную (·) 2. Rк > R ц 12

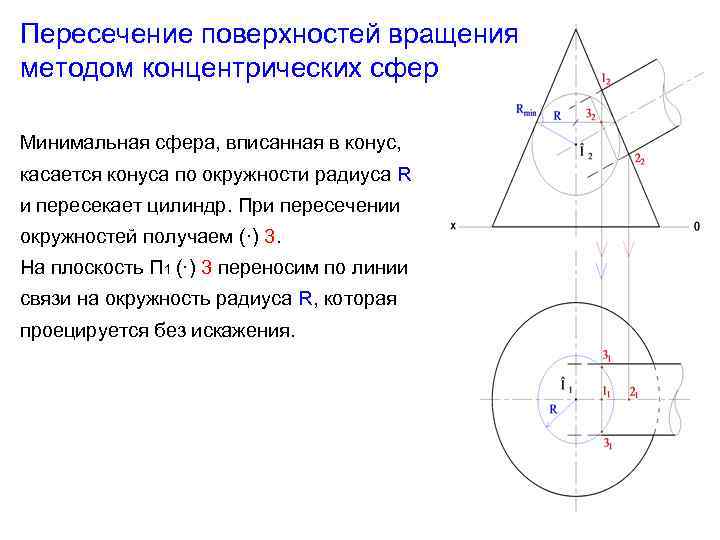Пересечение поверхностей вращения методом концентрических сфер Минимальная сфера, вписанная в конус, касается конуса по окружности радиуса R и пересекает цилиндр. При пересечении окружностей получаем (·) 3. На плоскость П 1 (·) 3 переносим по линии связи на окружность радиуса R, которая проецируется без искажения.

Пересечение поверхностей вращения методом концентрических сфер Задаем сферу произвольного радиуса, больше минимальной, но меньше максимальной. Она рассекает конус по двум окружностям, и цилиндр по одной. Окружности, пересекаясь, дают (·) 4 и 5.

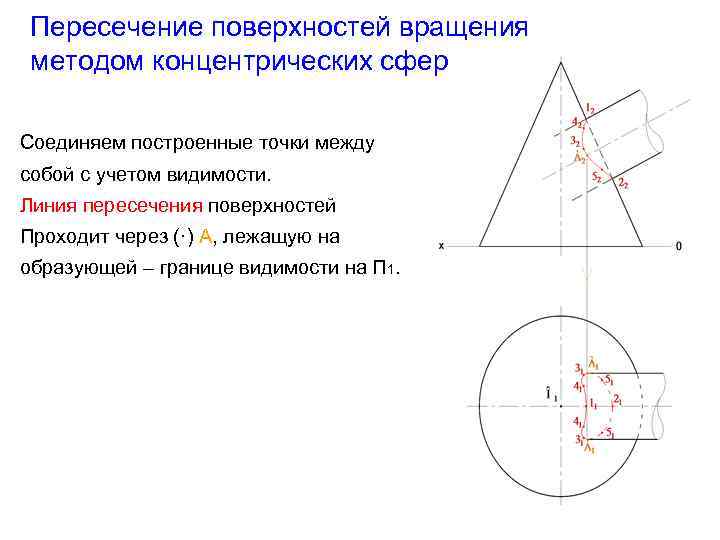Пересечение поверхностей вращения методом концентрических сфер Соединяем построенные точки между собой с учетом видимости. Линия пересечения поверхностей Проходит через (·) А, лежащую на образующей – границе видимости на П 1.

Пересечение поверхностей вращения методом эксцентрических сфер Метод эксцентрических сфер применяется в том случае, когда: 1. Пересекаются две поверхности вращения, или одна из них – циклическая. 2. Оси поверхностей скрещиваются. 3. Поверхности имеют общую плоскость симметрии.

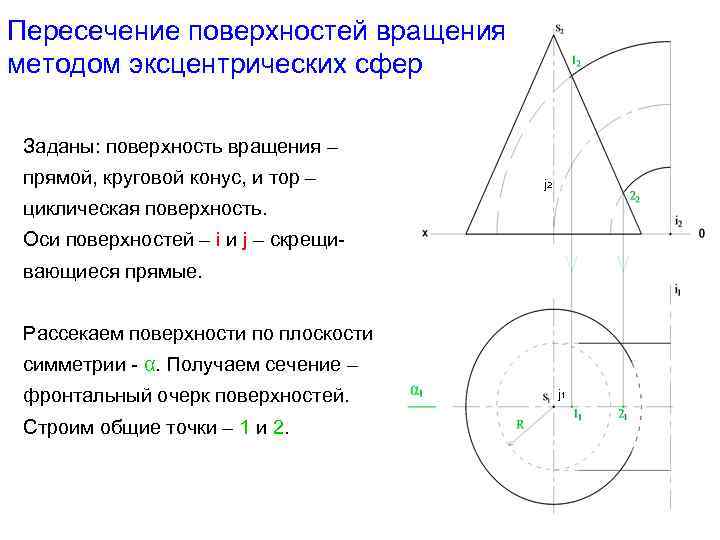Пересечение поверхностей вращения методом эксцентрических сфер Заданы: поверхность вращения – прямой, круговой конус, и тор – j 2 циклическая поверхность. Оси поверхностей – i и j – скрещивающиеся прямые. Рассекаем поверхности по плоскости симметрии - α. Получаем сечение – фронтальный очерк поверхностей. Строим общие точки – 1 и 2. j 1

Пересечение поверхностей вращения методом эксцентрических сфер Рассекаем поверхности фронтальноплоскостью β, проходящей через ось вращения тора i. В сечении тора получаем окружность. Из центра окружности (·) А восстанавливаем перпендикуляр до пересечения с осью конуса j в (·) А‘ является центром сферы, которая рассекает тор по указанной ранее окружности, и конус – по окружности радиуса R. Пересечением построенных окружностей является (·) 3.

Пересечение поверхностей вращения методом эксцентрических сфер Соединяем построенные точки между собой с учетом видимости. Линия пересечения поверхностей Проходит через (·) А, лежащую на образующей – границе видимости на П 1.