Лекция 7 Линейные Модели динамики авиационного двигателя

Лекция 7 Линейные Модели динамики авиационного двигателя

Применение линейных динамических моделей объясняется следующими причинами: 1. Многие динамические процессы в элементах САУ можно описать линейными моделями. 2. При малых отклонениях в сложных нелинейных системах относительно установившегося режима динамика системы является линейной. 3. Разработаны надежные и достаточно простые методы анализа и синтеза систем. 4. Легкость реализации линейного управления. 5. Для решения типовых задач управления используется единообразный математический аппарат. 6. Разработано обширное программное обеспечение анализа и синтеза линейных систем.

Формы представления линейной динамической модели 1. 2. 3. 4. Модель «Вход-Выход» Передаточная функция Частотная характеристика Модель в форме пространства состояния.

I. Модель «Вход-выход»

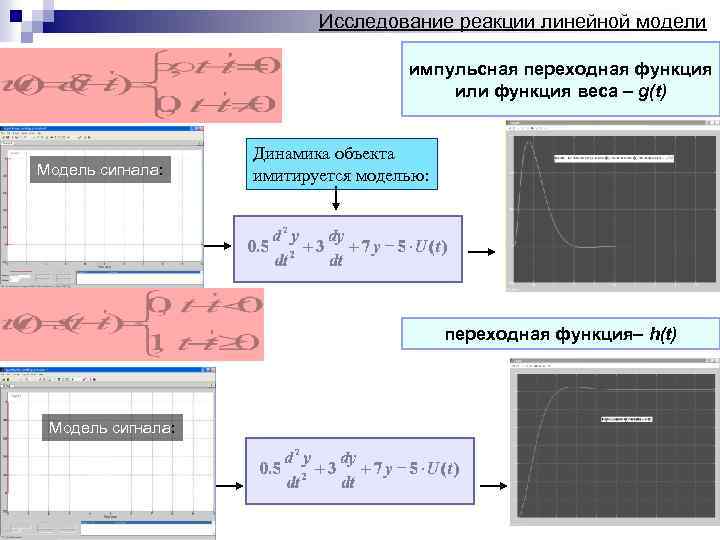Исследование реакции линейной модели импульсная переходная функция или функция веса – g(t) Модель сигнала: Динамика объекта имитируется моделью: переходная функция– h(t) Модель сигнала:

1. Решение дифференциального уравнения при условии, что входное воздействие есть дельта функция, будет представлять собой выходной сигнал, называемый импульсная переходная функция или функция веса – g(t) 2. Решение дифференциального уравнения при условии, что входное воздействие есть единичная ступенчатая функция, будет представлять собой выходной сигнал, называемый переходная функция – h(t) s(t) Свойство нормировки: h(t)

II. Передаточная функция динамической системы может быть получена как результат преобразования Лапласа ее импульсной переходной функции - g(t) , где p=с+jω комплексная переменная

Функция W(p) называется передаточной функцией динамической системы, модель которой задается линейным дифференциальным уравнением и представляет собой отношение изображений по Лапласу выходной координаты Y к входной координате U при нулевых начальных условиях. Модель динамической системы, представленной в форме передаточной функции удобна при исследовании и преобразовании структур динамических систем.

III. Частотная характеристика динамической системы может быть получена как результат преобразования Фурье ее импульсной переходной функции g(t) В теории управления рассматриваются только функции f(t), которые при t<0 f(t)=0. Поэтому интеграл преобразования Фурье приводится к виду:

Сравнение интегралов преобразования Лапласа и Фурье для диапазона (0 ) дает формальное равенство Учитывая формулу Эйлера преобразование Фурье импульсной переходной функции можно представить: (0<ω< )

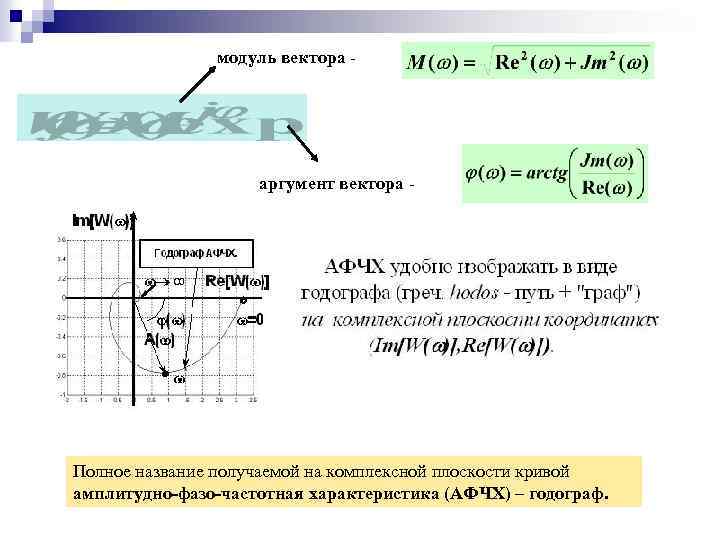модуль вектора - аргумент вектора - Полное название получаемой на комплексной плоскости кривой амплитудно-фазо-частотная характеристика (АФЧХ) – годограф.

Алгоритм построения частотной характеристики: 1. Выбрать модель объекта p = (jω) 2. Исключить мнимую единицу в знаменателе путем умножения W(jω) на комплексносопряженное число. 3. Найти модуль и аргумент:

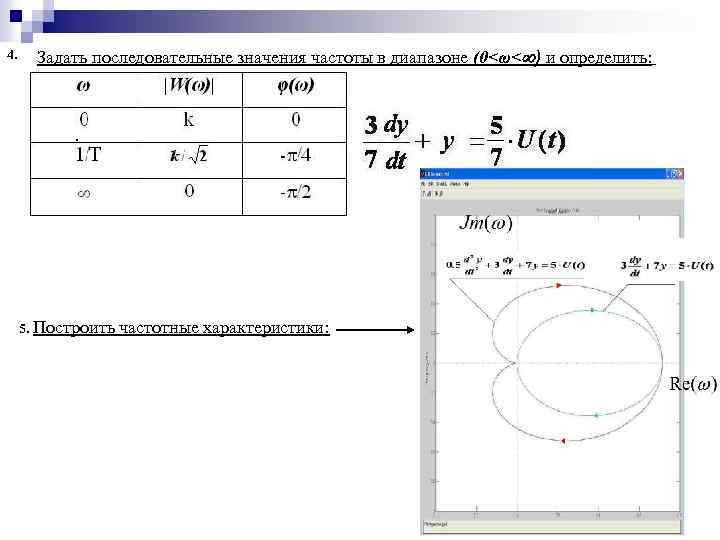4. Задать последовательные значения частоты в диапазоне (0<ω< ) и определить: . 5. Построить частотные характеристики:

Модель в форме пространства состояния Удобство представления модели в форме пространства состояния объясняется тем, что структура уравнений состояния совпадает с формой Коши, используемой при реализации численных процедур интегрирования во временной области.

Алгоритм преобразования

Алгоритм приведения к уравнениям состояния 1. Ввести фазовые переменные X=(x 1, x 2, …. . , xn) 2. Вычислить все производные по переменной y

3. Подставить вычисленные производные по переменной y в исходное дифференциальное уравнение 4. Вычислить значения неизвестных коэффициентов qi из условия исключения производных по переменной управления в правой части дифференциальной модели. Это достигается путем приравнивания коэффициентов уравнения в п. 3 при одинаковых производных по переменной управления. рекуррентные формулы определения коэффициентов qi:

5. Записать уравнение для старшей фазовой переменной xn , которое получается из уравнения, составленного в п. 3, после сокращений, выполненных в п. 4 6. Записать полученные уравнения состояния в стандартном матричном виде, который для уравнения третьего порядка имеет следующую структуру:

Матричный вид уравнений состояния

Y U U Y