Лекция 7 Кафедра физики ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ ПЛАН

Лекция 7 Кафедра физики ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ ПЛАН ЛЕКЦИИ 1. Распределение Максвелла • Средняя скорость молекулы • Средняя квадратичная скорость молекулы • Средняя кинетическая энергия поступательного движения 2. Распределение Больцмана 3. Барометрическая формула 4. Распределение Максвелла - Больцмана Общая физика. "Основы статистической физики" 1

Распределение Максвелла Перейдем от v к относительной скорости u, которая определяется формулой Как и абсолютная скорость v, относительная u – случайная величина. Функция распределения относительной скорости 2

ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ Определим с помощью закона усреднения среднюю скорость молекулы . 3

Кафедра физики ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ Вычислим последний интеграл. Сделаем замену переменной 4

Кафедра физики ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ Интеграл по х равен 1/2. В итоге получаем: Общая физика. "Основы статистической физики" 5

Кафедра физики ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ Используя закон усреднения, вычислим среднюю кинетическую энергию поступательного движения молекулы < > ▲Кинетическая энергия является однозначной функцией модуля скорости Применим общую формулу закона усреднения , 6

ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ Интеграл в этом выражении равен , Это средняя кинетическая энергия поступательного движения каждой молекулы 7

ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ Какой скоростью обладает молекула, кинетическая энергия которой равна средней кинетической энергии, то есть , Эта скорость называется “средняя квадратичная скорость” 8

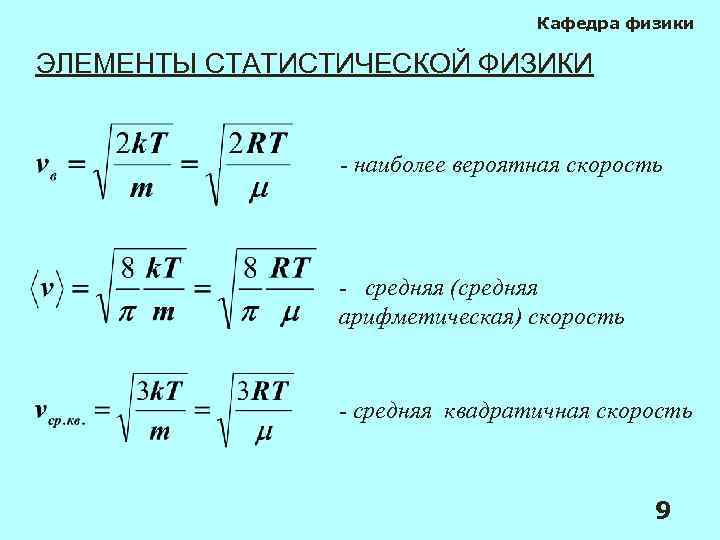Кафедра физики ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ - наиболее вероятная скорость , - средняя (средняя арифметическая) скорость - средняя квадратичная скорость 9

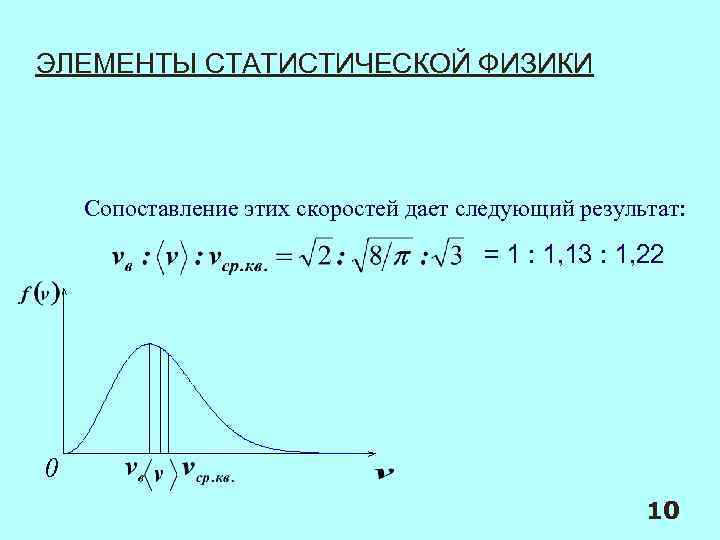ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ Сопоставление этих скоростей дает следующий результат: = 1 : 1, 13 : 1, 22 0 10

ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ Распределение Больцмана Займёмся функциями распределения координат Функция распределения координаты x – это такая функция f(x), умножение которой на ширину dx бесконечно малого интервала (x, x + dx) даёт вероятность d. W(x) того, что координата молекулы x попадёт в этот интервал (x, x + dx). Это вероятность попадания хаотически блуждающей в пространстве молекулы в фиксированную область пространства между двумя параллельными плоскостями, расположенными на расстоянии dx друг от друга. Это бесконечно малая область. 11

ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ Распределение Больцмана Рассмотрим бесконечно малую область пространства в виде параллелепипеда (элементарный объём). Определим вероятность d. W(x, y, z) попадания молекулы в фиксированный элементарный объём, расположенный в окрестности точки с координатами (x, y, z). Размеры элементарного объема - dx dy dz , объём - d. V = dx dy dz 12

ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ Распределение Больцмана Событие, вероятность которого мы собираемся определить, можно представить как три события: A – координата молекулы x попадает в интервал (x, x+dx), B – координата молекулы y попадает в интервал (y, y+dy), C – координата молекулы z попадает в интервал (z, z+dz). f 1(x), f 2 (y), f 3(z) – функции распределения координат молекулы (x, y, z) x, y и z – независимые характеристики микросостояния молекулы, поэтому события A, B и C – это независимые случайные события. 13

Распределение Больцмана Используя закон умножения вероятностей, найдем вероятность того, что события А, В, С произойдут одновременно: Определим вид произведения функций распределения 14

Распределение Больцмана Координаты и скорости – независимые параметры микросостояния частиц газа. Предположим, что функции распределения этих микропараметров похожи друг на друга (постулат № 1) Перемножим функции распределения проекций скорости 15

Распределение Больцмана Функция fм(vx, vy, vz), зависит от скоростей (vx, vy, vz) через кинетическую энергию . Разумно предположить, что произведение функций распределения координат f(x, y, z) тоже зависит от координат (x, y, z) через какую-то энергию, вероятнее всего, через потенциальную Wп (постулат № 2) Естественно предположить, что зависимость f(x, y, z) от Wп такая же, как и зависимость fм(vx, vy, vz) от , то есть экспоненциальная (постулат № 3) B – некоторый коэффициент 16

Распределение Больцмана Зная эту вероятность, можно по формуле для среднего числа событий определить среднее число молекул в элементарном объёме, находящемся в окрестности точки с координатами (x, y, z) N – полное число молекул в газе 17

Распределение Больцмана Отношение /d. V – это концентрация молекул n Пусть при n( x 0 , y 0 , z 0 ) Wп (x, y, z) =0. Тогда n( x 0 , y 0 , z 0 )= NB Это распределение Больцмана. 18

Распределение Больцмана. Барометрическая формула Построим модель атмосферы: 1. Температура воздуха с ростом высоты не меняется. 2. Воздух – это чистый идеальный газ. 3. Атмосфера – равновесная система. p = nk. T n 0 – концентрация молекул на уровне Земли Это барометрическая формула. p 0 – давление у поверхности Земли 19

Распределение Максвелла - Больцмана. Число молекул, компоненты скорости которых лежат в пределах от vx, vy, vz до vx + dvx , vy+dvy, vz+dvz , а координаты - в пределах от x, y, z до x+dx, y+dy, z+dz , равно - нормировочный множитель; 20