ЛЕКЦИЯ 7 ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ 4 1 Векторное уравнение

ЛЕКЦИЯ 7. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ 4. 1 Векторное уравнение для электромагнитного поля

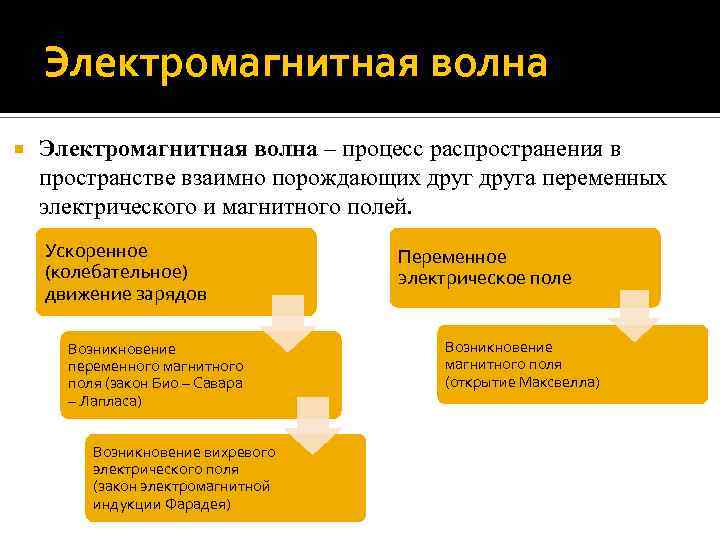Электромагнитная волна – процесс распространения в пространстве взаимно порождающих друга переменных электрического и магнитного полей. Ускоренное (колебательное) движение зарядов Возникновение переменного магнитного поля (закон Био – Савара – Лапласа) Возникновение вихревого электрического поля (закон электромагнитной индукции Фарадея) Переменное электрическое поле Возникновение магнитного поля (открытие Максвелла)

Уравнения Максвелла Покажем, что из уравнений Максвелла можно вывести волновое уравнение, которое описывает распространение в пространстве электромагнитной волны. Исходя из волнового уравнения найдем фазовую скорость электромагнитных волн. Система уравнений Максвелла в дифференциальной форме: здесь E – напряженность электрического поля, H – напряженность магнитного поля, B – вектор магнитной индукции, D – вектор электрической индукции, j – плотность тока проводимости, – объемная плотность сторонних электрических зарядов.

Уравнения Максвелла Пусть среда, в которой распространяется электромагнитная волна, является однородной и изотропной, электрически нейтральной ( = 0) и непроводящей (j = 0), кроме того, электрическая и магнитная проницаемости постоянны. Тогда справедливы соотношения (материальные уравнения): Тогда система уравнений Максвелла примет вид:

Вывод волнового уравнения из уравнений Максвелла Возьмем операцию rot от обеих частей первого уравнения. Ротор левой части равен: (в преобразованиях учтено, что E = div E = 0). Ротор правой части, с учетом третьего уравнения системы:

Вывод волнового уравнения из уравнений Максвелла Приравняем другу полученные выражения: Это равенство представляет собой волновое уравнение для вектора напряженности электрического поля E (электрической составляющей электромагнитной волны). Волновое уравнение для вектора H (магнитной составляющей волны) получается аналогично с помощью применения операции rot к третьему равнению системы:

Фазовая скорость электромагнитной волны Множитель при второй производной по времени векторов E и H равен квадрату величины, обратной фазовой скорости волны: Отсюда фазовая скорость электромагнитных волн:

Фазовая скорость электромагнитной волны Здесь введены следующие обозначения: - фазовая скорость электромагнитной волны в вакууме; - абсолютный показатель преломления среды; эта величина показывает, во сколько раз фазовая скорость электромагнитной волны в среде меньше ее скорости в вакууме.

ЛЕКЦИЯ 7. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ 4. 2 Плоская электромагнитная волна и ее свойства

Свойства электромагнитных волн Имея в виду, что: E = Exi + Eyj + Ezk, H = Hxi + Hyj + Hzk, представим уравнения Максвелла в виде:

Свойства электромагнитных волн Предположим, что э/м поле существует в виде плоской волны, распространяющейся в положительном направлении оси X. Тогда векторы E и H э/м поля зависят только от координаты x и не зависят от y и z: При этом производные от компонент векторов E и H по координатам x и y равны нулю:

Свойства электромагнитных волн Используя приведенные выше обстоятельства, упростим оператор «набла» : Подставим теперь векторы E и H в уравнения Максвелла. В результате получим следующую систему уравнений (см. следующий слайд):

Система уравнений Максвелла Вычислим определители и перемножим соответствующие компоненты векторов с скалярных произведениях

Система уравнений Максвелла Приравняем соответствующие множители при векторах i, j, k

Система уравнений Максвелла Проанализируем получившиеся 8 уравнений

Поперечность электромагнитной волны Из уравнений (3) и (4) следует, что Hx не зависит ни от x, ни от t, т. е. Hx = const. Аналогично, из уравнений (7) и (8) слудет, что и Ex = const. Поскольку Hx и Ex не меняются с течением времени и одинаковы во всех точках пространства, то эти поля являются статическими и не представляют собой колебательный процесс. Следовательно, Hx = 0 и Ex = 0. Таким образом, не равны нулю лишь компоненты Hy, Ez, Hz и Ey

Поперечность электромагнитных волн Таким образом, мы доказали первое свойство электромагнитных волн: электромагнитная волна является поперечной (в ней составляющие электрического и магнитного полей, параллельные направлению распространения волны, отсутствуют; векторы E и H перпендикулярны направлению ее распространения).

Взаимная перпендикулярность векторов E, H и K В не использованных пока уравнениях (1), (2), (5) и (6) содержатся переменные Ey, Hz, Ez, Hy. Эти уравнения могут быть представлены в виде 2 -х независимых систем уравнений, каждое из которых содержит только 2 переменные: (I) (II)

Взаимная перпендикулярность векторов E, H и K Эти системы описывают электромагнитные волны, которые возникают и существуют независимо одна от другой. Для дальнейшего изучения свойств волны достаточно ограничиться решением одной из систем. Рассмотрим первую.

Взаимная перпендикулярность векторов E, H и K Продифференцируем первое уравнение системы по переменной x и подставляя величину Hz/ x из второго уравнения системы, получим:

Взаимная перпендикулярность векторов E, H и K Дифференцируя второе уравнение системы по переменной x и подставляя величину Ez/ x из первого уравнения системы, аналогично получим:

Взаимная перпендикулярность векторов E, H и K Эти уравнения представляют собой частные случаи векторных волновых уравнений. Видно, что компоненты Ey и Hz удовлетворяют одному и тому же волновому уравнению. Э/м поле, являющееся решением этих двух уравнений, – плоская э/м волна, распространяющаяся вдоль оси X со скоростью

Взаимная перпендикулярность векторов E, H и K Волновой вектор K э/м волны коллинеарен оси X. Электрическую и магнитную составляющие э/м волны можно представить в виде: E = Eyj и H = Hzk. Таким образом, векторы E и H перпендикулярны друг к другу и к направлению распространения волны, т. е. волновому вектору K. Мы доказали второе свойство электромагнитных волн: в электромагнитной волне электрическая E и магнитная H составляющие перпендикулярны друг к другу и к волновому вектору K

Соотношения между модулями векторов E и H Решениями волновых уравнений являются, в частности, гармонические функции: Здесь - циклическая частота колебаний векторов E и H, k = /v – волновое число, v – фазовая скорость волны, 1, 2 – начальные фазы векторов E и H в точках с координатой x = 0 (начальные фазы колебаний источника волны)

Соотношения между модулями векторов E и H Найдем соотношения между компонентами Ey и Hz в данной точке пространства в определенный момент времени. Для этого подставим решения в первое уравнение системы:

Соотношения между модулями векторов E и H Для того, чтобы это равенство удовлетворялось при любых значениях x и t, необходимо, чтобы начальные фазы колебаний компонент Ey и Hz были одинаковы: 1 = 2. Тогда Таким образом, согласно третьему свойству электромагнитных волн, фазы колебаний их составляющих E и H одинаковы, а их амплитуды связаны соотношением

Правовинтовая система векторов E, H, K Итак, в э/м волне, распространяющейся в положительном направлении оси X, электрическая E и магнитная H составляющие изменяются с координатой x и временем t по закону:

Правая тройка векторов E, Н, k Итак, в э/м волне, распространяющейся в положительном направлении оси X, электрическая E и магнитная H составляющие изменяются с координатой x и временем t по закону: Причем, поскольку фазы компонент одинаковы, то в любой момент времени и в любой точке пространства векторы E, H и K образуют правую тройку (четвертое свойство электромагнитных волн).

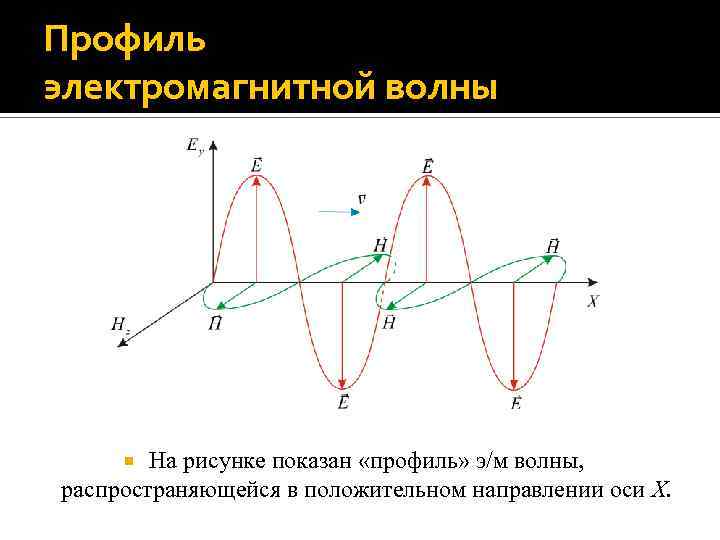Профиль электромагнитной волны На рисунке показан «профиль» э/м волны, распространяющейся в положительном направлении оси X.

ЛЕКЦИЯ 7. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ 4. 3 Энергия и импульс электромагнитных волн

Объемная плотность энергии электромагнитной волны Пусть электромагнитная волна (далее – ЭМВ) распространяется в вакууме ( = = 1). Энергия ЭМВ складывается из энергии электрического и магнитного полей, при этом объемная плотность энергии w складывается из двух слагаемых – объемных плотностей энергии электрического we и магнитного wm полей: Учтем третье свойство ЭМВ – соотношение между амплитудами электрической и магнитной составляющих (в вакууме):

Объемная плотность энергии электромагнитной волны Имеем: Таким образом, объемная плотность энергии ЭМВ равна Здесь E и H – модели векторов напряженностей электрического и магнитного полей соответственно, c – скорость ЭМВ в вакууме.

Вектор Умова - Пойнтинга Вектор плотности потока энергии, переносимой ЭМВ, или иначе вектор Умова – Пойнтинга, как и соответствующий вектор для упругой волны, равен произведению объемной плотности энергии w ЭМВ на скорость c ее распространения: Здесь вектор n – нормаль к волновой поверхности. Учитывая четвертое свойство ЭМВ, S || K , т. е. S E и H. Тогда

Интенсивность электромагнитной волны В соответствии с определением, интенсивность I ЭМВ равна модулю среднего по временем значения вектора плотности потока энергии (вектора Умова - Пойнтинга): Если направление ЭМВ в пространстве не изменяется, то n = const и

Интенсивность электромагнитной волны С учетом третьего свойства ЭМВ, Таким образом, интенсивность ЭМВ пропорциональна квадрату амплитуды Em колебаний вектора напряженности магнитного поля.

Давление электромагнитного поля на вещество Падая на поверхность вещества, ЭМВ производит давление, передавая поверхности импульс, равный импульсу единица объема вещества: Электрическая компонента E ЭМВ, согласно закону Ома, вызывает в веществе ток плотностью j = (1/ уд)E При этом заряды будут двигаться по вектору j (или E). Магнитная составляющая H ЭМВ действует на них с силой Ампера FА = [j 0 H]d. V, направленной внутрь вещества, вызывая давление на поверхность.

Давление электромагнитной волны на вещество Величина давления p, оказываемого ЭМВ на поверхность вещества: Давление ЭМВ в рассматриваемом случае полного поглощения ЭМВ поверхностью тела равно объемной плотности энергии w волны.