Лекция 7 Экономико-математические модели применяемые в землеустройстве Денисова

Лекция 7. Экономико-математические модели, применяемые в землеустройстве Денисова С. Т. Старший преподаватель n кафедры ММи. МЭ. n n 1

План 1. Формирование экономико-математической модели задач, решаемых симплексным методом. 2. Определение расстояний между основными полосами 3. Дробно- линейные критерии оптимальности. 4. Экономико-математическое моделирование производственного процесса

Экономико-математические модели, применяемые в землеустройстве n Экономико-математические методы и моделирование в землеустройстве позволяют решать большой круг задач, связанных с оптимизацией территориальной организации с/х производства с учетом агроэкологических свойств земли, установлением рациональных размеров и структуры землевладений и землепользований, оптимизацией трансформации и улучшения угодий, размещением севооборотов, повышения плодородия почв, проектированием системы противоэрозионных мероприятий, моделированием производственного процесса.

1. Формирование экономико-математической модели задач, решаемых симплексным методом. • Ограничение по земельным ресурсам можно разбить на n две подгруппы. • В первую подгруппу входят ограничения, связанные с использованием пашни, естественных сенокосов и пастбищ, многолетних насаждений. • где xj –площади искомых с/х культур • bik – площади с/х угодий i-го вида • xki – площадь k- го вида угодий, подлежащая трансформации в i – ый вид. 4

• Во вторую группу ограничений по земельным ресурсам входят ограничения по структуре использованию пашни. Здесь необходимо учесть агробиологические и n агротехнические требования к возделываемым культурам, их чередованию в схемах севооборотов. Для этого по основным культурам необходимо учесть удельный вес их к общей площади посевов, по ряду культур необходимо соблюдение определенных пропорций. Условия, учитывающие требования севооборотов, могут быть выражены различными способами, взаимно дополняющими друга. • Отдельными ограничениями могут быть выражены соотношения между группами культур или отдельными культурами, если они связаны между собой. 5

2. Определение расстояний между основными полосами В ходе землеустройства ставится задача установить оптимальную ширину межполосного пространства, от которой зависит каркас организации территории в районах, где защитные лесные полосы имеют значительную агрохозяйственную ценность. Наиболее полно данный вопрос с использованием производственных функций исследован И. М. Стативкой. Для оценки зависимости прибавки урожая кукурузы (У) от высоты лесной полосы (Х) была использована производственная функция, имеющая вид логарифмической параболы. Применив метод наименьших квадратов, вычисляют коэффициенты. 6

3. Дробно- линейные критерии оптимальности n К задачам дробно- линейного программирования приводятся задачи, в которых критерием оптимальности служат себестоимость продукции, рентабельность производства, производительность труда. 7

n Ввели новые переменные, след-о: 8

Экономико-математическое моделирование производственного процесса n n Постановку экономико-математической задачи в данном проекте можно сформулировать как определение количества трудовых ресурсов определенной квалификации и материально-технических средств, вовлеченных в проект. Выполнение работ производилось силами двух основных отделов предприятия: землеустроительного (ЗО) и отдела цифровой картографии (ОЦК). Средний уровень оклада составляет: для инженера первой категории 24 тысячи рублей, инженера второй категории 17 тысяч рублей, техника 11 тысяч рублей. . Средняя стоимость рабочего места, оборудованного современной картографической станцией составляет 2000 условных единиц, Pentium 4 – 1000, Pentium 3 – 500.

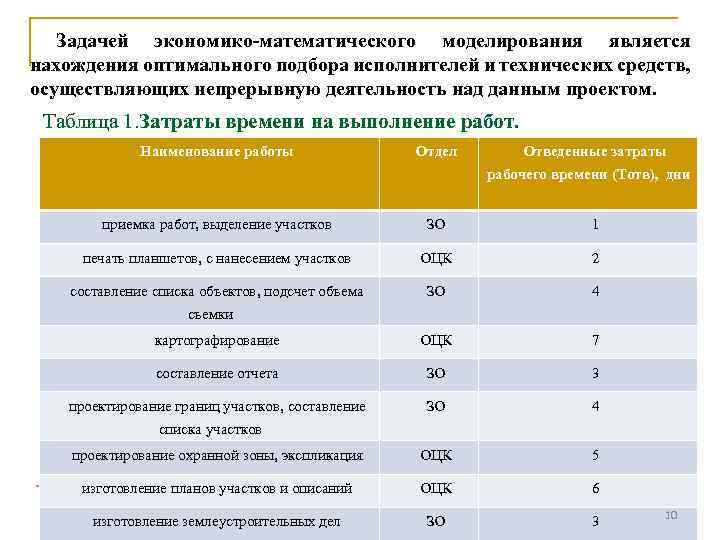Задачей экономико-математического моделирования является нахождения оптимального подбора исполнителей и технических средств, осуществляющих непрерывную деятельность над данным проектом. Таблица 1. Затраты времени на выполнение работ. Наименование работы Отдел Отведенные затраты рабочего времени (Тотв), дни приемка работ, выделение участков ЗО 1 печать планшетов, с нанесением участков ОЦК 2 составление списка объектов, подсчет объема ЗО 4 картографирование ОЦК 7 составление отчета ЗО 3 проектирование границ участков, составление ЗО 4 проектирование охранной зоны, экспликация ОЦК 5 изготовление планов участков и описаний ОЦК 6 изготовление землеустроительных дел ЗО 3 съемки списка участков 10

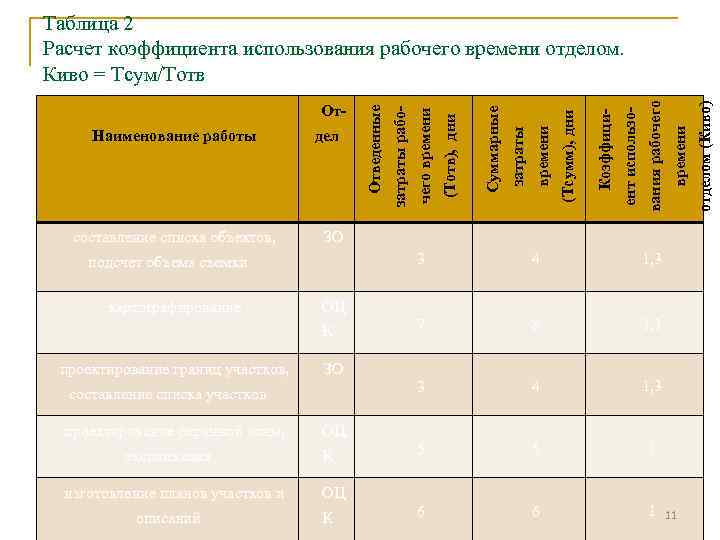составление списка объектов, экспликация изготовление планов участков и описаний 1, 3 7 8 1, 1 3 4 1, 3 5 5 1 6 6 1 ЗО ОЦ К 11 отделом (Киво) времени вания рабочего ент использо- Коэффици- (Тсумм), дни времени 4 ОЦ составление списка участков проектирование охранной зоны, затраты 3 К проектирование границ участков, Суммарные ЗО подсчет объема съемки картографирование (Тотв), дни дел чего времени Наименование работы затраты рабо- Отведенные Таблица 2 Расчет коэффициента использования рабочего времени отделом. Киво = Тсум/Тотв

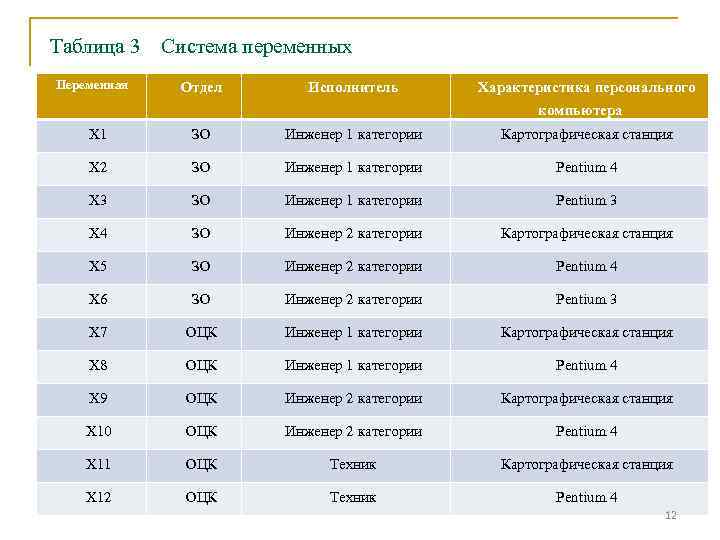Таблица 3 Переменная Система переменных Отдел Исполнитель Характеристика персонального компьютера Х 1 ЗО Инженер 1 категории Картографическая станция Х 2 ЗО Инженер 1 категории Pentium 4 Х 3 ЗО Инженер 1 категории Pentium 3 Х 4 ЗО Инженер 2 категории Картографическая станция Х 5 ЗО Инженер 2 категории Pentium 4 Х 6 ЗО Инженер 2 категории Pentium 3 Х 7 ОЦК Инженер 1 категории Картографическая станция Х 8 ОЦК Инженер 1 категории Pentium 4 Х 9 ОЦК Инженер 2 категории Картографическая станция Х 10 ОЦК Инженер 2 категории Pentium 4 Х 11 ОЦК Техник Картографическая станция Х 12 ОЦК Техник Pentium 4 12

Составление экономико-математической модели n n n В качестве критерия оптимальности данной модели выступает минимум ресурсных затрат. Стоимость привлечения исполнителя равна величине его заработной платы на расчетный период (5 месяцев), вовлечение технических средств оценивается рыночной стоимостью их приобретения. Таким образом, целевая функция примет вид: Z(X)=84*Х 1+54*Х 2+39*Х 3+77*Х 4+47*Х 5+32*Х 6+84*Х 7+54*Х 8+ 77*Х 9+47*Х 10+71*Х 11+41*Х 12 → min (1) Систему ограничений можно сформулировать следующим образом: ∑Кирim * Хi ≥ ∑ Кивоm (2) где: m – вид работы, соответствующий номеру ограничения, i – исполнитель, обеспеченный конкретным рабочим местом. 13

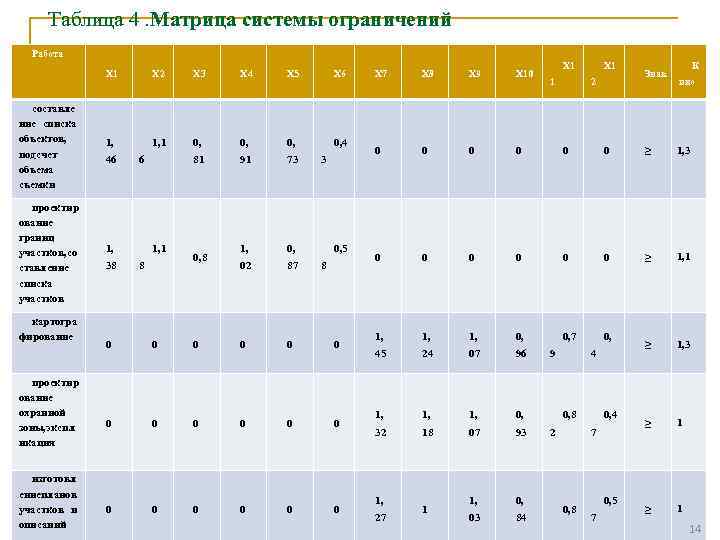Таблица 4. Матрица системы ограничений Работа Х 1 Х 2 Х 3 Х 4 Х 5 Х 6 составле ние списка объектов, подсчет объема съемки 1, 1 0, 0, 4 81 91 73 проектир ование границ участков, со ставление списка участков 1, 0, 02 87 картогра фирование проектир ование охранной зоны, экспл икация изготовл ениепланов участков и описаний 46 38 6 1, 1 8 0, 8 3 0, 5 8 0 0 0 0 0 Х 1 Х 8 Х 9 Х 10 0 0 0 ≥ 1, 3 0 0 0 ≥ 1, 1 1, 1, 0, 7 0, 45 24 07 96 ≥ 1, 3 1, 1, 0, 32 18 07 93 ≥ 1 1, 03 84 ≥ 1 1, 27 1 1 2 9 4 0, 8 2 0, 4 7 0, 8 0, 5 7 Знак К Х 7 иво 14

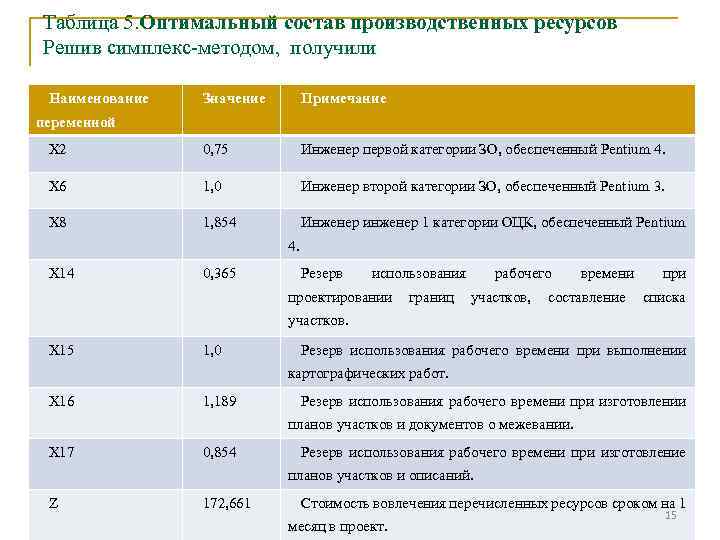Таблица 5. Оптимальный состав производственных ресурсов Решив симплекс-методом, получили Наименование Значение Примечание Х 2 0, 75 Инженер первой категории ЗО, обеспеченный Pentium 4. X 6 1, 0 Инженер второй категории ЗО, обеспеченный Pentium 3. Х 8 1, 854 Инженер инженер 1 категории ОЦК, обеспеченный Pentium переменной 4. Х 14 0, 365 Резерв использования проектировании границ рабочего участков, времени составление при списка участков. Х 15 1, 0 Резерв использования рабочего времени при выполнении картографических работ. Х 16 1, 189 Резерв использования рабочего времени при изготовлении планов участков и документов о межевании. Х 17 0, 854 Резерв использования рабочего времени при изготовление планов участков и описаний. Z 172, 661 Стоимость вовлечения перечисленных ресурсов сроком на 1 месяц в проект. 15