Лекция 7 Дельта-электроны Их характеристики 1 Ионизационные потери

Лекция 7 Дельта-электроны. Их характеристики 1. Ионизационные потери с учетом макс. передачи энергии 2. δ-электроны 3. Кривая Ландау Процесс многократного рассеяния 1. Упругое рассеяние частиц на ядрах 2. Сопоставление рассеяние тяжелой частицы на электроне и на ядре 3. Процесс многократного рассеяния в слое вещества 4. Оценка среднего значения квадрата угла рассеяния 5. Среднеквадратичный угол многократного рассеяния 6. Движение заряженных частиц в магнитном поле 7. Влияние многократного рассеяния

Ионизационные потери с учетом макс. передачи энергии удельных ионизационные потери Переданная энергия электрону среды , вылетающему под углом ψ: Те = M 1 e Энергия максимальна (Temax ) для угла вылета Если Т 1 >> M 1 с2, максимальная передача энергии электрону может быть близка значению Tеmax = Т 1 Несмотря на малую передачу энергии электрону, которая в среднем составляет десятки э. В, возможны значительные флуктуации в сторону энергий, значительно превышающих потенциал ионизации атомов.

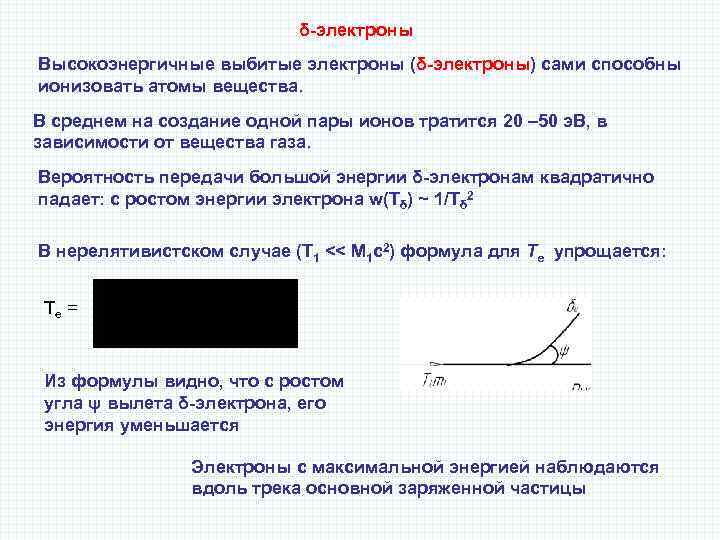δ-электроны Высокоэнергичные выбитые электроны (δ-электроны) сами способны ионизовать атомы вещества. В среднем на создание одной пары ионов тратится 20 – 50 э. В, в зависимости от вещества газа. Вероятность передачи большой энергии δ-электронам квадратично падает: с ростом энергии электрона w(Тδ) ~ 1/Tδ 2 В нерелятивистском случае (Т 1 << M 1 c 2) формула для Те упрощается: Те = Из формулы видно, что с ростом угла ψ вылета δ-электрона, его энергия уменьшается Электроны с максимальной энергией наблюдаются вдоль трека основной заряженной частицы

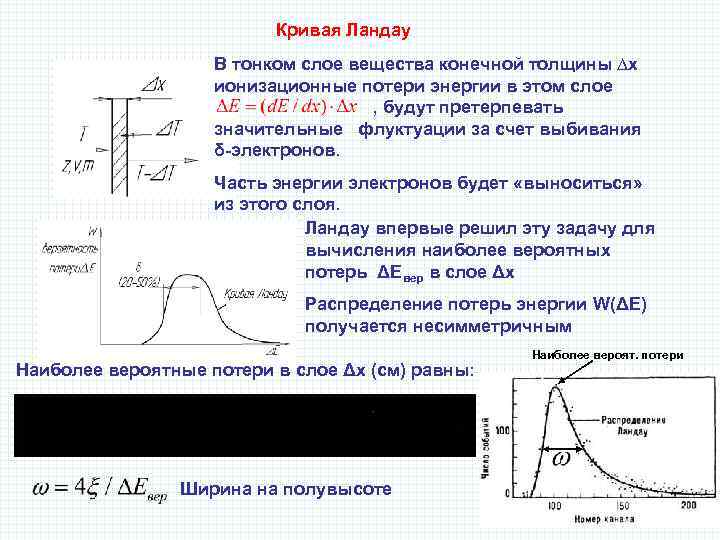Кривая Ландау В тонком слое вещества конечной толщины ∆х ионизационные потери энергии в этом слое , будут претерпевать значительные флуктуации за счет выбивания δ-электронов. Часть энергии электронов будет «выноситься» из этого слоя. Ландау впервые решил эту задачу для вычисления наиболее вероятных потерь ΔΕвер в слое Δх Распределение потерь энергии W(ΔE) получается несимметричным Наиболее вероятные потери в слое Δх (см) равны: Ширина на полувысоте Наиболее вероят. потери

Применимость распределения Ландау • • Потери энергии флуктуируют по нормальному закону, если средняя величина потери энергии во всем слое будет значительно больше максимальной энергии дельта-электрона. Для тяжелых налетающих частиц и не слишком высоких энергий можно получить значение: • Нормальный закон применим, если • В противном случае получается условие применимости распределения Ландау - сильные флуктуации потерь энергии в конечном слое вещества-детектора.

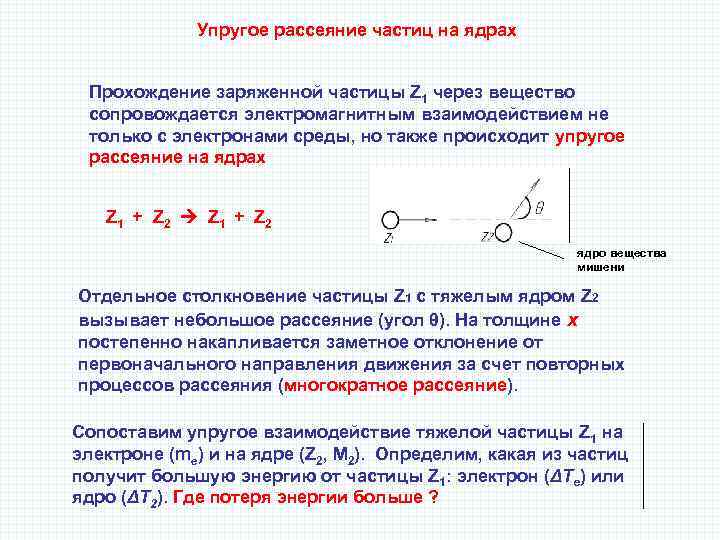Упругое рассеяние частиц на ядрах Прохождение заряженной частицы Z 1 через вещество сопровождается электромагнитным взаимодействием не только с электронами среды, но также происходит упругое рассеяние на ядрах Z 1 + Z 2 ядро вещества мишени Отдельное столкновение частицы Z 1 с тяжелым ядром Z 2 вызывает небольшое рассеяние (угол θ). На толщине х постепенно накапливается заметное отклонение от первоначального направления движения за счет повторных процессов рассеяния (многократное рассеяние). Сопоставим упругое взаимодействие тяжелой частицы Z 1 на электроне (me) и на ядре (Z 2, M 2). Определим, какая из частиц получит большую энергию от частицы Z 1: электрон (ΔΤе) или ядро (ΔΤ 2). Где потеря энергии больше ?

Упругое рассеяние тяжелой частицы на электроне и на ядре Сопоставим упругое взаимодействие тяжелой частицы Z 1 на электроне (me) и на ядре (Z 2, M 2). Определим, какая из частиц получит большую энергию от частицы Z 1: электрон (ΔΤе) или ядро (ΔΤ 2). частица Z 1 пролетает мимо электрона и ядра с одинаковым прицельным параметром ρ и с одинаковой скоростью V 1

Упругого рассеяния тяжелой частицы на электроне и на ядре

Процесс многократного рассеяния в слое вещества Условия расчета: Частица, проходя толстый слой, не должна заметно терять энергию: T 1(x =0) ≈ T 1(x). Импульс частицы р1 при этом остается практически постоянным по глубине. Это ограничивает верхнее значение толщины вещества и применимость используемых приближений. Суммарный угол θ =Σ θi, где θi – рассеяние в i-ом взаимодействии, не может служить мерой рассеяния. Его величина, с учетом знака углов отклонений θi, равна нулю. Принято оценивать квадратичный угол: = Σ θi 2 Для учета взаимодействия частицы Z 1 с отдельным ядром i можно использовать формулу Резерфорда

Оценка среднего значения квадрата угла рассеяния Для отдельного столкновения с ядром Расчет в приближении малых углов - в расчетах взято Значения предельных углов связаны с размерами ядра (Rяд) и атома (Rат) и зависят от материала вещества-мишени .

Среднеквадратичный угол многократного рассеяния m = σ·n·x Суммарный среднеквадратичный угол многократного рассеяния получается как сумма значений по полному числу отдельных i независимых столкновений m на толщине х. σ(см 2) – полное резерфордовское сечение рассеяния n(1/cм 3) – концентрация ядер мишени Х (см) – толщина мишени L - длина взаимодействия Получается функциональная зависимость вида: Заряженная частица (Z 1), движущаяся с импульсом р1 (скорость v 1) через вещество толщиной х, приобретает среднеквадратичный угол Точные расчеты дают подобную зависимость:

Движение заряженных частиц в магнитном поле Заряженная частица q с импульсом р1, попадает в однородное магнитное поле перпендикулярно вектору Н. Частица будет двигаться равномерно по окружности с радиусом R. На эту частицу действует сила Лоренца (запись в системе единиц CGSE) и центростремительная сила Их равенство позволяет вычислить величину радиуса вращения в магнитном поле Эта запись справедлива и для релятивистского случая Получаем:

Влияние многократного рассеяния Пусть, например заряженная частица попадает в магнитный спектрометр (заполненный веществом) и проходит расстояние d перпендикулярно направлению поля Н по дуге окружности. При этом она поворачивается на угол На толщине спектрометра d отношение угла многократного рассеяния к углу поворота в магнитном поле запишется в виде Скорость частицы через импульс выражается При определенных сочетаниях параметров частицы, поля и характеристик среды искажающее влияние многократного рассеяния может быть минимизировано.