 Лекция 7(2 ч). Симметрия и ее связь с законами сохранения
Лекция 7(2 ч). Симметрия и ее связь с законами сохранения
 Вопросы: § Принципы симметрии в неживой и живой природе § Симметрия кристаллов § Симметрия пространства и времени § Внутренние симметрии § Общие и частные законы сохранения § Связь законов сохранения со свойствами симметрии физических систем
Вопросы: § Принципы симметрии в неживой и живой природе § Симметрия кристаллов § Симметрия пространства и времени § Внутренние симметрии § Общие и частные законы сохранения § Связь законов сохранения со свойствами симметрии физических систем
 Принципы симметрии в неживой и живой природе • Обобщенное понятие симметрии • Симметрия - это инвариантность (неизменность) свойств некоторой (физической) системы при изменении (преобразовании) ее параметров. • Если законы, устанавливающие соотношение между величинами, характеризующими систему (или определяющие изменение этих величин со временем) не меняются при определенных преобразованиях, которым может быть подвергнута система, то говорят, что эти законы обладают симметрией (или инвариантны) относительно данных преобразований. В естествознании преобладают определения категорий симметрии и асимметрии, основанные на перечислении определенных признаков. Например, симметрия определяется через совокупность свойств порядка, однородности, соразмерности, гармоничности.
Принципы симметрии в неживой и живой природе • Обобщенное понятие симметрии • Симметрия - это инвариантность (неизменность) свойств некоторой (физической) системы при изменении (преобразовании) ее параметров. • Если законы, устанавливающие соотношение между величинами, характеризующими систему (или определяющие изменение этих величин со временем) не меняются при определенных преобразованиях, которым может быть подвергнута система, то говорят, что эти законы обладают симметрией (или инвариантны) относительно данных преобразований. В естествознании преобладают определения категорий симметрии и асимметрии, основанные на перечислении определенных признаков. Например, симметрия определяется через совокупность свойств порядка, однородности, соразмерности, гармоничности.
 Симметрия кристаллов • Элементы теории групп Наиболее разработана теория симметрии у кристаллов. Здесь под симметрией понимается свойство кристаллов "совмещаться" самим с собой при поворотах, отражениях, параллельных переносах, либо при выполнении части или комбинации этих действий (операций). Симметрия внешней формы (иногда говорят, огранки) кристалла определяется симметрией его атомного (т. е. дискретного трехмерно-периодического) строения, которая, в свою очередь, обусловливает также и симметрию физических свойств кристалла. Поскольку кристаллы – это объекты трехмерного пространства, то теория их симметрии – это теория симметричных преобразований самого пространства в себя с учетом вида конкретной кристаллической решетки. Причем, при этих преобразованиях само пространство не деформируется, а преобразуется как жесткое целое; такие преобразования называются ортогональными (или изометрическими).
Симметрия кристаллов • Элементы теории групп Наиболее разработана теория симметрии у кристаллов. Здесь под симметрией понимается свойство кристаллов "совмещаться" самим с собой при поворотах, отражениях, параллельных переносах, либо при выполнении части или комбинации этих действий (операций). Симметрия внешней формы (иногда говорят, огранки) кристалла определяется симметрией его атомного (т. е. дискретного трехмерно-периодического) строения, которая, в свою очередь, обусловливает также и симметрию физических свойств кристалла. Поскольку кристаллы – это объекты трехмерного пространства, то теория их симметрии – это теория симметричных преобразований самого пространства в себя с учетом вида конкретной кристаллической решетки. Причем, при этих преобразованиях само пространство не деформируется, а преобразуется как жесткое целое; такие преобразования называются ортогональными (или изометрическими).
 Симметрия кристаллов
Симметрия кристаллов
 Симметрия кристаллов
Симметрия кристаллов
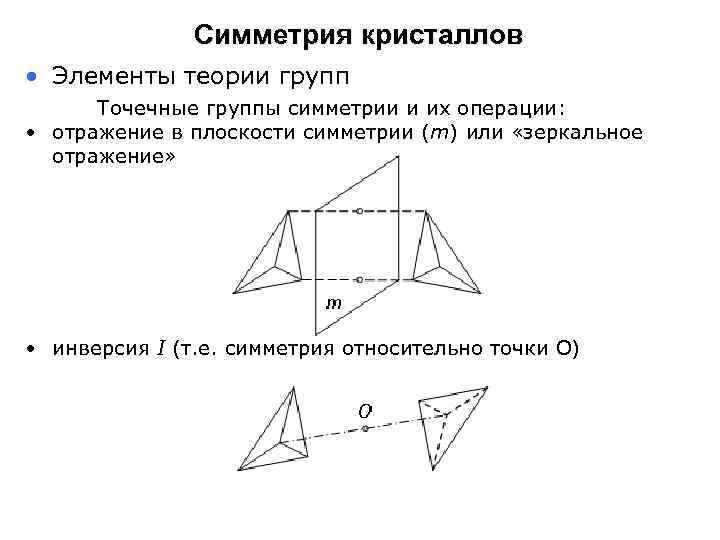 Симметрия кристаллов • Элементы теории групп Точечные группы симметрии и их операции: • отражение в плоскости симметрии (m) или «зеркальное отражение» • инверсия I (т. е. симметрия относительно точки О)
Симметрия кристаллов • Элементы теории групп Точечные группы симметрии и их операции: • отражение в плоскости симметрии (m) или «зеркальное отражение» • инверсия I (т. е. симметрия относительно точки О)
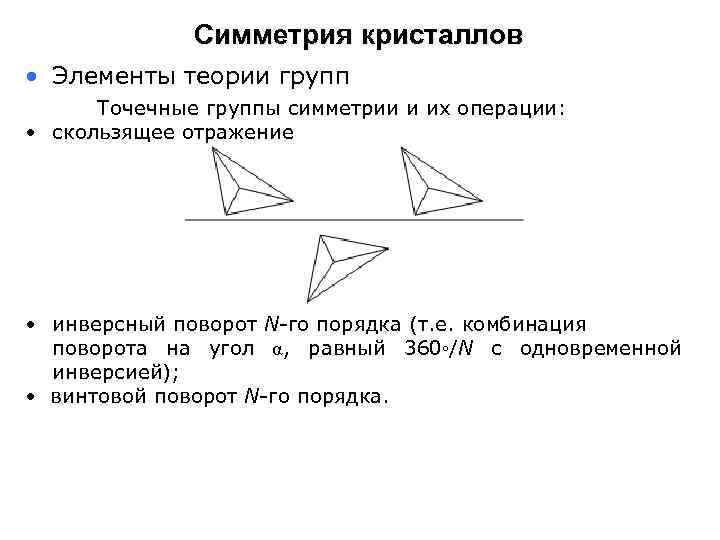 Симметрия кристаллов • Элементы теории групп Точечные группы симметрии и их операции: • скользящее отражение • инверсный поворот N-го порядка (т. е. комбинация поворота на угол α, равный 360◦/N с одновременной инверсией); • винтовой поворот N-го порядка.
Симметрия кристаллов • Элементы теории групп Точечные группы симметрии и их операции: • скользящее отражение • инверсный поворот N-го порядка (т. е. комбинация поворота на угол α, равный 360◦/N с одновременной инверсией); • винтовой поворот N-го порядка.
 Симметрия кристаллов Точечные группы описывают симметрию не только кристаллов, но и любых конечных объектов (фигур). В живой природе часто наблюдается запрещенная в кристаллографии симметрия с осями 5 -го, 7 -го порядков. Например, для описания регулярной структуры сферических вирусов оказалась важной икосаэдрическая точечная группа « 532» (с пятиугольником в основании).
Симметрия кристаллов Точечные группы описывают симметрию не только кристаллов, но и любых конечных объектов (фигур). В живой природе часто наблюдается запрещенная в кристаллографии симметрия с осями 5 -го, 7 -го порядков. Например, для описания регулярной структуры сферических вирусов оказалась важной икосаэдрическая точечная группа « 532» (с пятиугольником в основании).
 Симметрия кристаллов
Симметрия кристаллов
 Симметрия кристаллов
Симметрия кристаллов
 Симметрия пространства и времени • Непрерывные преобразования пространствавремени Опыт показывает, что физические законы симметричны относительно следующих наиболее общих преобразований пространства-времени. • Перенос (сдвиг) системы как целого в пространстве. Замечание. Это и последующие пространственновременные преобразования будем рассматривать в двух аспектах: 1) как активное преобразование, т. е. реальный перенос физической системы относительно выбранной системы отсчета; 2) или как пассивное преобразование, т. е. параллельный перенос самой системы отсчета. Симметрия физических законов относительно сдвигов в пространстве означает эквивалентность всех точек пространства, т. е. – предполагает однородность пространства (отсутствие в нем особых, выделенных точек со специальными свойствами).
Симметрия пространства и времени • Непрерывные преобразования пространствавремени Опыт показывает, что физические законы симметричны относительно следующих наиболее общих преобразований пространства-времени. • Перенос (сдвиг) системы как целого в пространстве. Замечание. Это и последующие пространственновременные преобразования будем рассматривать в двух аспектах: 1) как активное преобразование, т. е. реальный перенос физической системы относительно выбранной системы отсчета; 2) или как пассивное преобразование, т. е. параллельный перенос самой системы отсчета. Симметрия физических законов относительно сдвигов в пространстве означает эквивалентность всех точек пространства, т. е. – предполагает однородность пространства (отсутствие в нем особых, выделенных точек со специальными свойствами).
 Симметрия пространства и времени • Непрерывные преобразования пространствавремени • Поворот системы как целого в пространстве. Симметрия физических законов относительно поворотов в пространстве означает эквивалентность всех направлений в пространстве, т. е. – предполагает изотропность пространства. • Изменение начала отсчета времени (сдвиг во времени). Симметрия относительно сдвига во времени означает, что физические законы не меняются со временем. • Переход к системе отсчета, движущейся относительно данной системы с постоянной скоростью. Симметрия относительно этого преобразования означает, в частности, эквивалентность всех инерциальных систем отсчета. Замечание. Все указанные выше симметрии отражают псевдоевклидову геометрию четырехмерного пространствавремени (пространственно-временного континуума).
Симметрия пространства и времени • Непрерывные преобразования пространствавремени • Поворот системы как целого в пространстве. Симметрия физических законов относительно поворотов в пространстве означает эквивалентность всех направлений в пространстве, т. е. – предполагает изотропность пространства. • Изменение начала отсчета времени (сдвиг во времени). Симметрия относительно сдвига во времени означает, что физические законы не меняются со временем. • Переход к системе отсчета, движущейся относительно данной системы с постоянной скоростью. Симметрия относительно этого преобразования означает, в частности, эквивалентность всех инерциальных систем отсчета. Замечание. Все указанные выше симметрии отражают псевдоевклидову геометрию четырехмерного пространствавремени (пространственно-временного континуума).
 Симметрия пространства и времени • Дискретные преобразования пространствавремени Создание релятивистской квантовой теории привело к открытию нового типа симметрии, являющейся, в отличие от перечисленных выше, дискретной. • С – означает, что все законы физики одинаковы для частиц и соответствующих им античастиц, т. е. , как говорят, должно - выполняться зарядовое сопряжение; • Р – означает, что законы инвариантны для любого явления (объекта) и его «зеркального» образа (отражения), т. е. допускается, как говорят, пространственная инверсия; • Т – означает возможность обращения времени, т. е. законы одинаковы при движении системы (из частиц и античастиц) как вперед, так и назад. При изменении направления движения всех частиц и античастиц на обратное – система вернется в исходное состояние.
Симметрия пространства и времени • Дискретные преобразования пространствавремени Создание релятивистской квантовой теории привело к открытию нового типа симметрии, являющейся, в отличие от перечисленных выше, дискретной. • С – означает, что все законы физики одинаковы для частиц и соответствующих им античастиц, т. е. , как говорят, должно - выполняться зарядовое сопряжение; • Р – означает, что законы инвариантны для любого явления (объекта) и его «зеркального» образа (отражения), т. е. допускается, как говорят, пространственная инверсия; • Т – означает возможность обращения времени, т. е. законы одинаковы при движении системы (из частиц и античастиц) как вперед, так и назад. При изменении направления движения всех частиц и античастиц на обратное – система вернется в исходное состояние.
 Симметрия пространства и времени • Дискретные преобразования пространствавремени Относительно отдельных дискретных С-, Р- и Тпреобразований оказываются симметричными процессы, обусловленные сильными и электромагнитными взаимодействиями. В процессах слабого взаимодействия нарушается симметрия относительно пространственной инверсии (Р) и зарядового сопряжения (С), однако сохраняется симметрия относительно преобразования комбинированной инверсии (СР), а, следовательно, согласно «СРТ-теореме» , и относительно обращения времени (Т). Формулировка СРТ-теоремы была дана в 1954 г. Г. Людерсом, а – доказана в 1955 г. В. Паули. • Если в природе происходит некоторый процесс, то точно также в ней может происходить и «СРТ-сопряженный процесс» , в котором все частицы заменены на античастицы, проекции спинов – изменили знак, а начальные и конечные состояния процесса – поменялись местами.
Симметрия пространства и времени • Дискретные преобразования пространствавремени Относительно отдельных дискретных С-, Р- и Тпреобразований оказываются симметричными процессы, обусловленные сильными и электромагнитными взаимодействиями. В процессах слабого взаимодействия нарушается симметрия относительно пространственной инверсии (Р) и зарядового сопряжения (С), однако сохраняется симметрия относительно преобразования комбинированной инверсии (СР), а, следовательно, согласно «СРТ-теореме» , и относительно обращения времени (Т). Формулировка СРТ-теоремы была дана в 1954 г. Г. Людерсом, а – доказана в 1955 г. В. Паули. • Если в природе происходит некоторый процесс, то точно также в ней может происходить и «СРТ-сопряженный процесс» , в котором все частицы заменены на античастицы, проекции спинов – изменили знак, а начальные и конечные состояния процесса – поменялись местами.
 Симметрия пространства и времени
Симметрия пространства и времени
 Внутренние симметрии • Под внутренними симметриями понимают симметрии между частицами и полями с различными квантовыми числами (характеристиками). К внутренним симметриям относят: 1) изотопическую инвариантность, которая наблюдается при сильных взаимодействиях, симметричных относительно поворотов в особом «изотопическом пространстве» (одним из проявлений этой симметрии является зарядовая независимость ядерных сил); следует заметить, что изотопическая инвариантность не является строгой симметрией: она нарушается электромагнитным взаимодействием частиц и различием в массах u- и dкварков; 2) «цветовую» симметрию, которая свойственна сильному взаимодействию между кварками в ходе образования адронов; 3) симметрию между кварками и лептонами, которая была на опыте замечена в ходе изучения их электрослабого взаимодействия.
Внутренние симметрии • Под внутренними симметриями понимают симметрии между частицами и полями с различными квантовыми числами (характеристиками). К внутренним симметриям относят: 1) изотопическую инвариантность, которая наблюдается при сильных взаимодействиях, симметричных относительно поворотов в особом «изотопическом пространстве» (одним из проявлений этой симметрии является зарядовая независимость ядерных сил); следует заметить, что изотопическая инвариантность не является строгой симметрией: она нарушается электромагнитным взаимодействием частиц и различием в массах u- и dкварков; 2) «цветовую» симметрию, которая свойственна сильному взаимодействию между кварками в ходе образования адронов; 3) симметрию между кварками и лептонами, которая была на опыте замечена в ходе изучения их электрослабого взаимодействия.
 Общие и частные законы сохранения
Общие и частные законы сохранения
 • Общие и частные законы сохранения Частные и общие (фундаментальные) законы Деформация нарушает их внутреннее равновесие, которое после снятия нагрузки – восстанавливается. Таким образом, силы упругости – по сути электромагнитные силы и по существу отражают электрический эффект. Также закон валентности при образовании химических соединений – определяет создание общих электронных пар, т. е. внутренне это тоже – электрический эффект. Однако в приведенных примерах обычно не прибегают к рассмотрению уравнений электродинамики, а ограничиваются для описания внешнего поведения системы перечисленными законами. Такие законы называются частными, т. е. выполняются для определенной частной области естествознания. Когда же исследователи абстрагируются от внешней стороны эффекта и раскрывают его внутренний механизм, то целый ряд на первый взгляд не связанных явлений – объединяются в системы и классы. И уже эти системы могут быть описаны одним, общим законом, который называют фундаментальным.
• Общие и частные законы сохранения Частные и общие (фундаментальные) законы Деформация нарушает их внутреннее равновесие, которое после снятия нагрузки – восстанавливается. Таким образом, силы упругости – по сути электромагнитные силы и по существу отражают электрический эффект. Также закон валентности при образовании химических соединений – определяет создание общих электронных пар, т. е. внутренне это тоже – электрический эффект. Однако в приведенных примерах обычно не прибегают к рассмотрению уравнений электродинамики, а ограничиваются для описания внешнего поведения системы перечисленными законами. Такие законы называются частными, т. е. выполняются для определенной частной области естествознания. Когда же исследователи абстрагируются от внешней стороны эффекта и раскрывают его внутренний механизм, то целый ряд на первый взгляд не связанных явлений – объединяются в системы и классы. И уже эти системы могут быть описаны одним, общим законом, который называют фундаментальным.
 Общие и частные законы сохранения • Фундаментальные законы сохранения для изолированных систем Если рассматриваются так называемые законы сохранения, то они не теряют своего смысла при замене одной системы на другую. • Законы сохранения – это физические закономерности, согласно которым численные значения некоторых физических величин не изменяются со временем в любых процессах или в определенном классе процессов. Так как во многих случаях динамический закон для данной системы – неизвестен (или слишком сложен), то в этом случае именно закон сохранения позволяет сделать некоторые заключения о характере поведения системы (о ее возможных состояниях).
Общие и частные законы сохранения • Фундаментальные законы сохранения для изолированных систем Если рассматриваются так называемые законы сохранения, то они не теряют своего смысла при замене одной системы на другую. • Законы сохранения – это физические закономерности, согласно которым численные значения некоторых физических величин не изменяются со временем в любых процессах или в определенном классе процессов. Так как во многих случаях динамический закон для данной системы – неизвестен (или слишком сложен), то в этом случае именно закон сохранения позволяет сделать некоторые заключения о характере поведения системы (о ее возможных состояниях).
 Общие и частные законы сохранения
Общие и частные законы сохранения
 Общие и частные законы сохранения • Законы сохранения в микромире Большую роль законы сохранения играют в микромире, в квантовой теории поля, в физике элементарных частиц. Здесь работают правила отбора, согласно которым реакции с элементарными частицами, которые привели бы к нарушению того или иного закона сохранения, - не могут осуществляться в природе. В дополнение к перечисленным выше фундаментальным законам сохранения, имеющимся в макромире, в физике элементарных частиц сформулировано много специфических законов сохранения, позволяющих интерпретировать наблюдаемые на опыте правила отбора. К строгим законам сохранения в микромире относят: • закон сохранения барионного заряда, выполняющийся во всех, известных на сегодня, видах взаимодействий, и которому соответствует правило отбора ΔB = 0; • закон сохранения лептонного заряда и выполнение соответствующего правила отбора ΔL = 0.
Общие и частные законы сохранения • Законы сохранения в микромире Большую роль законы сохранения играют в микромире, в квантовой теории поля, в физике элементарных частиц. Здесь работают правила отбора, согласно которым реакции с элементарными частицами, которые привели бы к нарушению того или иного закона сохранения, - не могут осуществляться в природе. В дополнение к перечисленным выше фундаментальным законам сохранения, имеющимся в макромире, в физике элементарных частиц сформулировано много специфических законов сохранения, позволяющих интерпретировать наблюдаемые на опыте правила отбора. К строгим законам сохранения в микромире относят: • закон сохранения барионного заряда, выполняющийся во всех, известных на сегодня, видах взаимодействий, и которому соответствует правило отбора ΔB = 0; • закон сохранения лептонного заряда и выполнение соответствующего правила отбора ΔL = 0.
 • Общие и частные законы сохранения Законы сохранения в микромире К нестрогим законам сохранения относят: • закон сохранения изотопического спина (т. е. должно соблюдаться ΔI= 0), который выполняется только при сильном взаимодействии; • законы сохранения «странности» (Δs = 0), «шарма» (Δc = 0), «красоты» (Δb = 0), т. е. , в целом, сохранение «аромата» , которые выполняются при сильном и электромагнитном взаимодействиях, но нарушаются в слабых взаимодействиях. Замечание. Таким образом, и исследования в физике элементарных частиц также напоминают о необходимости проверки известных законов сохранения в каждой области явлений природы. Некоторые современные мыслители, например, акад. Н. Ф. Овчинников, считают, что абсолютны не законы сохранения, а сама идея сохранения.
• Общие и частные законы сохранения Законы сохранения в микромире К нестрогим законам сохранения относят: • закон сохранения изотопического спина (т. е. должно соблюдаться ΔI= 0), который выполняется только при сильном взаимодействии; • законы сохранения «странности» (Δs = 0), «шарма» (Δc = 0), «красоты» (Δb = 0), т. е. , в целом, сохранение «аромата» , которые выполняются при сильном и электромагнитном взаимодействиях, но нарушаются в слабых взаимодействиях. Замечание. Таким образом, и исследования в физике элементарных частиц также напоминают о необходимости проверки известных законов сохранения в каждой области явлений природы. Некоторые современные мыслители, например, акад. Н. Ф. Овчинников, считают, что абсолютны не законы сохранения, а сама идея сохранения.
 • Связь законов сохранения со свойствами симметрии физических систем Теорема Нётер Наличие той или иной симметрии приводит к тому, что для данной системы существует некоторая сохраняющаяся физическая величина. Если известны свойства (параметры) симметрии некоторой физической системы, то, как правило, можно установить для нее законы сохранения, и наоборот. Здесь очень важна теорема, сформулированная немецким математиком Эмми Нётер в 1918 г. и устанавливающая связь между симметрией и законами сохранения. Формулировка. Для физической системы (уравнения движения которой имеют форму системы дифференциальных уравнений и могут быть получены из вариационного принципа механики) каждому, непрерывно зависящему от одного параметра, преобразованию, оставляющему инвариантным действие (D), соответствует закон сохранения.
• Связь законов сохранения со свойствами симметрии физических систем Теорема Нётер Наличие той или иной симметрии приводит к тому, что для данной системы существует некоторая сохраняющаяся физическая величина. Если известны свойства (параметры) симметрии некоторой физической системы, то, как правило, можно установить для нее законы сохранения, и наоборот. Здесь очень важна теорема, сформулированная немецким математиком Эмми Нётер в 1918 г. и устанавливающая связь между симметрией и законами сохранения. Формулировка. Для физической системы (уравнения движения которой имеют форму системы дифференциальных уравнений и могут быть получены из вариационного принципа механики) каждому, непрерывно зависящему от одного параметра, преобразованию, оставляющему инвариантным действие (D), соответствует закон сохранения.
 Связь законов сохранения со свойствами симметрии физических систем
Связь законов сохранения со свойствами симметрии физических систем
 Связь законов сохранения со свойствами симметрии физических систем • Теорема Нётер Так, согласно теореме Нетер, - • из инвариантности относительно сдвига во времени следует закон сохранения энергии; • из инвариантности относительно пространственных сдвигов (это обусловлено однородностью самого пространства) следует закон сохранения импульса; • из инвариантности относительно пространственного вращения (это обусловлено изотропностью пространства) следует закон сохранения момента импульса.
Связь законов сохранения со свойствами симметрии физических систем • Теорема Нётер Так, согласно теореме Нетер, - • из инвариантности относительно сдвига во времени следует закон сохранения энергии; • из инвариантности относительно пространственных сдвигов (это обусловлено однородностью самого пространства) следует закон сохранения импульса; • из инвариантности относительно пространственного вращения (это обусловлено изотропностью пространства) следует закон сохранения момента импульса.
 Связь законов сохранения со свойствами симметрии физических систем • Теорема Нётер распространяется не только на пространственно-временные симметрии, но и на внутренние симметрии, обусловленные внутренними свойствами элементарных частиц (так называемые калибровочные симметрии). Пример. Так, из независимости динамики заряженных частиц в электромагнитных полях от соответствующих калибровочных преобразований следует закон сохранения электрического заряда. Релятивистская инвариантность заряда и закон сохранения заряда изолированной системы – взаимно обусловливают друга и принимаются в качестве исходного положения классической электродинамики.
Связь законов сохранения со свойствами симметрии физических систем • Теорема Нётер распространяется не только на пространственно-временные симметрии, но и на внутренние симметрии, обусловленные внутренними свойствами элементарных частиц (так называемые калибровочные симметрии). Пример. Так, из независимости динамики заряженных частиц в электромагнитных полях от соответствующих калибровочных преобразований следует закон сохранения электрического заряда. Релятивистская инвариантность заряда и закон сохранения заряда изолированной системы – взаимно обусловливают друга и принимаются в качестве исходного положения классической электродинамики.


