Лекция 7 1 Транспортная задача Экономико-математическая модель задачи

Лекция 7 1. Транспортная задача. Экономико-математическая модель задачи. 2. Составление первого плана перевозок методом наименьших затрат 3. Проверка оптимальности плана перевозок методом потенциалов (алгоритм метода потенциалов). 4. Обоснование алгоритма метода потенциалов. 5. Решение транспортной задачи в системе Mathcad.

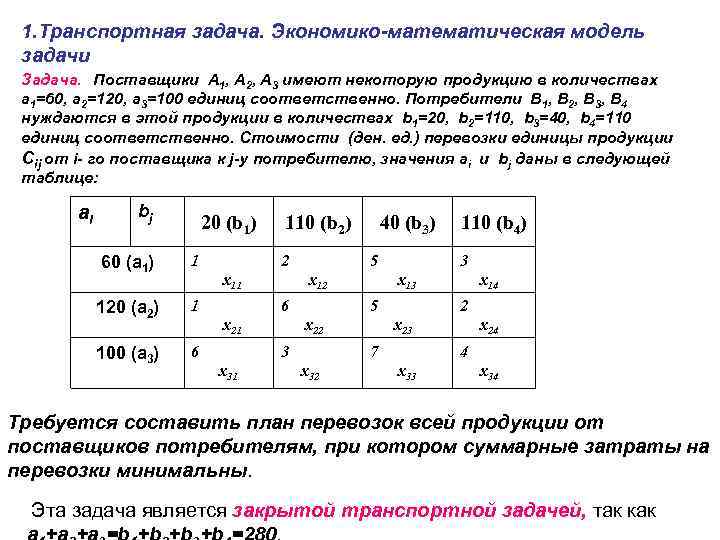1. Транспортная задача. Экономико-математическая модель задачи Задача. Поставщики А 1, А 2, А 3 имеют некоторую продукцию в количествах а 1=60, а 2=120, а 3=100 единиц соответственно. Потребители В 1, В 2, В 3, В 4 нуждаются в этой продукции в количествах b 1=20, b 2=110, b 3=40, b 4=110 единиц соответственно. Стоимости (ден. ед. ) перевозки единицы продукции Cij от i- го поставщика к j-у потребителю, значения ai и bj даны в следующей таблице: ai bj 20 (b 1) 60 (a 1) 1 120 (a 2) 1 100 (a 3) 6 110 (b 2) 2 x 11 5 x 12 6 x 21 x 13 x 22 x 14 2 x 23 7 x 32 110 (b 4) 3 5 3 x 31 40 (b 3) x 24 4 x 33 x 34 Требуется составить план перевозок всей продукции от поставщиков потребителям, при котором суммарные затраты на перевозки минимальны. Эта задача является закрытой транспортной задачей, так как

Пусть xij - объем перевозки от i -го поставщика к j -у потребителю Мощности поставщиков должны быть реализованы ai bj 20 (b 1) 60 (a 1) (7. 2) 120 (a 2) 1 100 (a 3) (7. 1) 1 6 110 (b 2) 2 x 11 5 x 12 6 x 21 110 (b 4) 3 x 13 5 x 22 3 x 31 40 (b 3) x 14 2 x 23 7 x 32 x 24 4 x 33 x 34 Спросы всех потребителей должны быть удовлетворены Суммарные затраты на перевозки должны быть минимальными (7. 3)

Математическая формулировка задачи На множестве неотрицательных решений системы уравнений (7. 1)(7. 2) найти такое решение при котором функция (7. 3) принимает наименьшее значение Замечание. Мы имеем задачу линейного программирования в канонической форме. В этой системы 6 линейно независимых уравнений (т. е. ранг системы равен 6). Это означает, что число базисных переменных равно 6. 2. Составление первого плана перевозок методом наименьших затрат Составим первый план перевозок. В этом плане отличными от нуля перевозками могут быть лишь m+n -1 = 3+4 -1=6 значений (базисные переменные), где m число поставщиков, n число потребителей. Остальные значения заведомо равны нулю (свободные переменные).

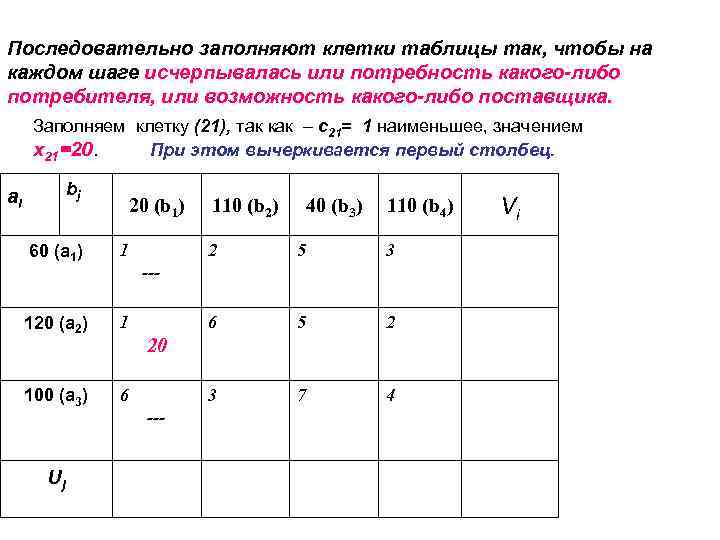Последовательно заполняют клетки таблицы так, чтобы на каждом шаге исчерпывалась или потребность какого-либо потребителя, или возможность какого-либо поставщика. Заполняем клетку (21), так как с21= 1 наименьшее, значением x 21=20. При этом вычеркивается первый столбец. bj ai 20 (b 1) 60 (a 1) 1 120 (a 2) 1 100 (a 3) 6 Uj 110 (b 2) 40 (b 3) 110 (b 4) 2 5 3 6 5 2 3 7 4 --- 20 --- Vi

Заполняем остальные клетки: (1, 2), (2, 4), (3, 2), (3, 4), (3, 3) ai bj 60 (a 1) 120 (a 2) 20 (b 1) 1 110 (b 2) 2 ___ 1 5 6 6 ___ 3 50 110 (b 4) ___ 60 20 100 (a 3) 40 (b 3) ___ 2 ___ 7 100 4 40 10

3. Проверка оптимальности плана перевозок методом потенциалов (алгоритм метода потенциалов). В чем заключается метод потенциалов? 1. Вводится строка потенциалов { Uj } и столбец потенциалов { V i }. Принимая, например, U 1 =0, остальные значения Uj и Vi определяются так, чтобы для заполненных клеток выполнялось равенство (7. 4) 2. Вычисляются оценки пустых (прочеркнутых) клеток по формуле: (7. 5) План является оптимальным, если оценки всех пустых клеток неотрицательны, т. е.

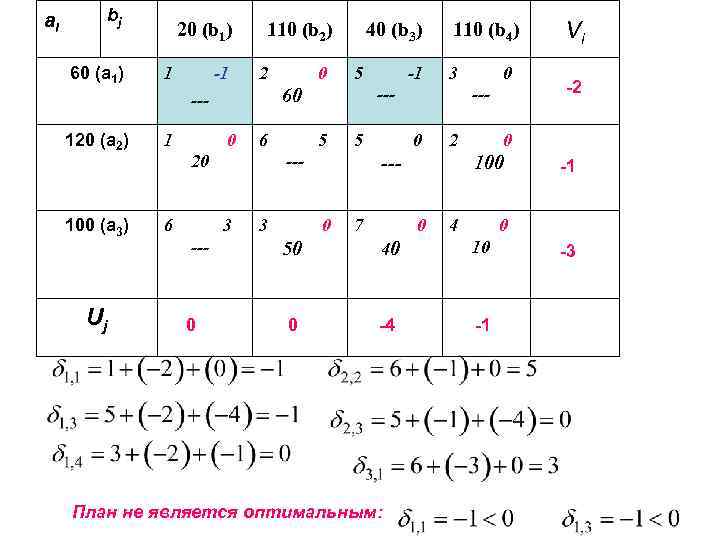ai bj 60 (a 1) 20 (b 1) 1 -1 110 (b 2) 2 100 (a 3) Uj 1 0 6 20 6 0 5 3 -1 110 (b 4) 3 --5 --3 --- 5 60 --120 (a 2) 0 40 (b 3) --0 2 --0 7 0 4 -1 0 50 40 10 0 -4 -1 План не является оптимальным: -2 0 100 0 Vi -3

Дадим поставку в клетку (1, 3) и построим цикл пересчета. Циклом в таблице называют ломаную с вершинами в клетках: 1. Ломаная должна быть связной; 2. В каждой вершине ломаной встречаются два звена, одно из которых располагается по строке, другое по столбцу; Циклом пересчета называют такой цикл в таблице с базисным распределением поставок, при котором одна из его вершин лежит в свободной клетке, остальные – в заполненных. Поставка, передаваемая по циклу, определяется как минимум среди поставок цикла в клетках со знаком « - » .

План не является оптимальным ! ai bj 60 (a 1) 20 (b 1) 1 -1 110 (b 2) 2 60 --120 (a 2) 1 100 (a 3) 6 Uj 0 0 6 20 40 (b 3) 5 - --- 5 5 --3 3 50 0 0 + Цикл пересчета Получаем новый план поставок 3 Vi 0 -2 --- + 0 2 0 100 -1 0 4 0 10 40 _ -3 --0 7 --- -1 110 (b 4) -4 -1

ai bj 20 (b 1) 60 (a 1) 1 120 (a 2) 1 100 (a 3) 6 Uj -1 110 (b 2) 2 0 40 (b 3) 5 6 20 5 5 --3 3 3 40 20 0 0 110 (b 4) 1 7 2 90 --- 0 0 -3 0 100 1 --- -2 --- --0 0 Vi -1 0 -3 4 10 -1 Методом потенциалов проверяем оптимальность плана План не является оптимальным.

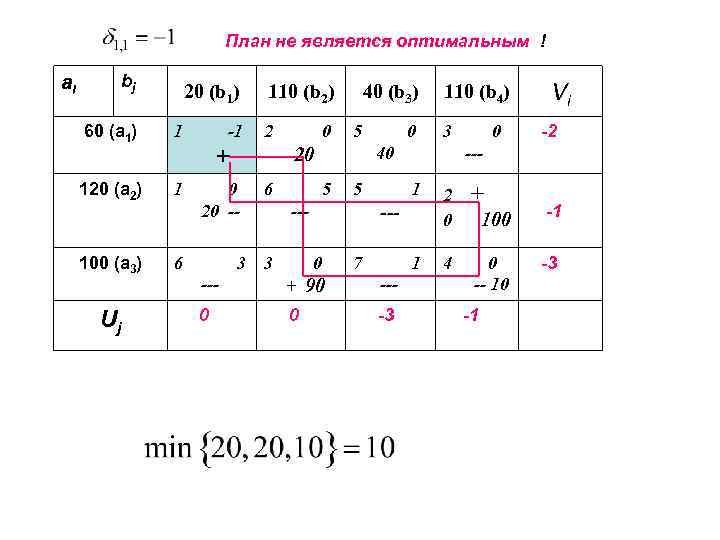План не является оптимальным ! ai bj 20 (b 1) 60 (a 1) 1 120 (a 2) 1 100 (a 3) Uj -1 110 (b 2) 2 5 0 20 -- 6 5 5 --- 3 3 0 110 (b 4) 1 7 1 --- + 90 --- 0 0 -3 -2 --- --0 Vi 0 3 40 -- 20 + 6 0 40 (b 3) 2 0 + 100 -1 4 0 -- 10 -3 -1

Новый базисный план поставок ai bj 60 (a 1) 20 (b 1) 1 110 (b 2) 2 100 (a 3) Uj 1 5 6 10 6 --- 3 5 --- 3 --7 100 110 (b 4) 40 10 10 120 (a 2) 40 (b 3) --2 110 4 --- Vi

ai bj 60 (a 1) 20 (b 1) 1 0 110 (b 2) 2 1 100 (a 3) 6 Uj 5 6 10 4 3 --- -1 2 --- 100 0 --0 7 -1 110 1 4 ---4 Vi -1 3 5 --4 110 (b 4) 40 10 10 120 (a 2) 40 (b 3) 1 --- -1 План является оптимальным Оптимальный план не является единственным ! -2

Оптимальный план не является единственным ! ai bj 60 (a 1) 20 (b 1) 1 0 110 (b 2) 2 100 (a 3) Uj 5 1 6 --- 6 4 3 --- -1 2 1 4 ---4 -1 110 10 100 0 --0 7 Vi -1 3 5 --4 110 (b 4) 30 10 20 120 (a 2) 40 (b 3) 1 --- -1 -2

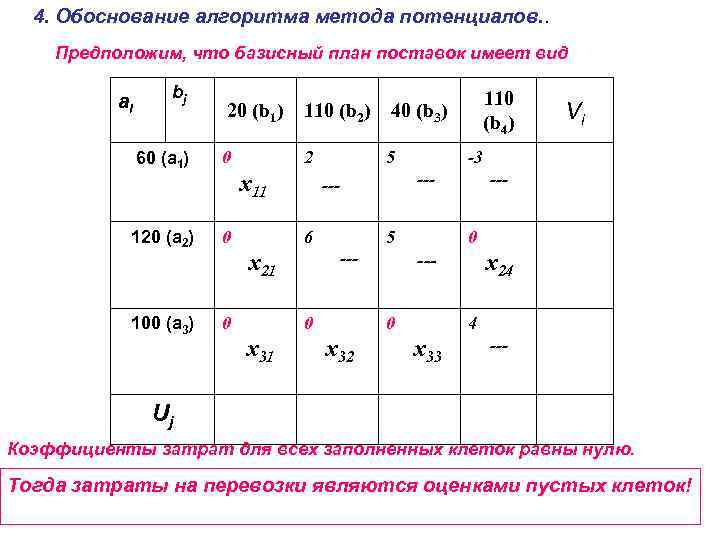4. Обоснование алгоритма метода потенциалов. . Предположим, что базисный план поставок имеет вид ai bj 60 (a 1) 20 (b 1) 0 110 (b 2) 2 x 11 120 (a 2) 0 100 (a 3) 0 5 6 5 --- 0 x 31 --0 x 32 Vi -3 --- x 21 110 (b 4) 40 (b 3) x 24 4 x 33 --- Uj Коэффициенты затрат для всех заполненных клеток равны нулю. Тогда затраты на перевозки являются оценками пустых клеток!

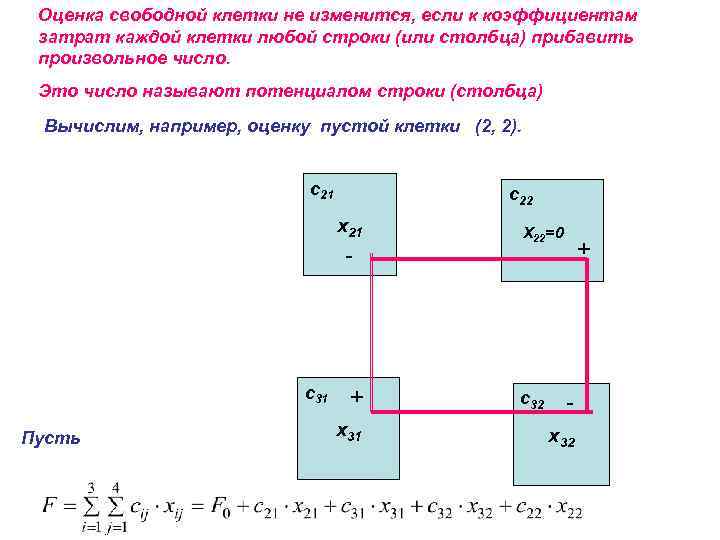Оценка свободной клетки не изменится, если к коэффициентам затрат каждой клетки любой строки (или столбца) прибавить произвольное число. Это число называют потенциалом строки (столбца) Вычислим, например, оценку пустой клетки (2, 2). c 21 c 22 x 21 - c 31 Пусть + x 31 X 22=0 c 32 + x 32

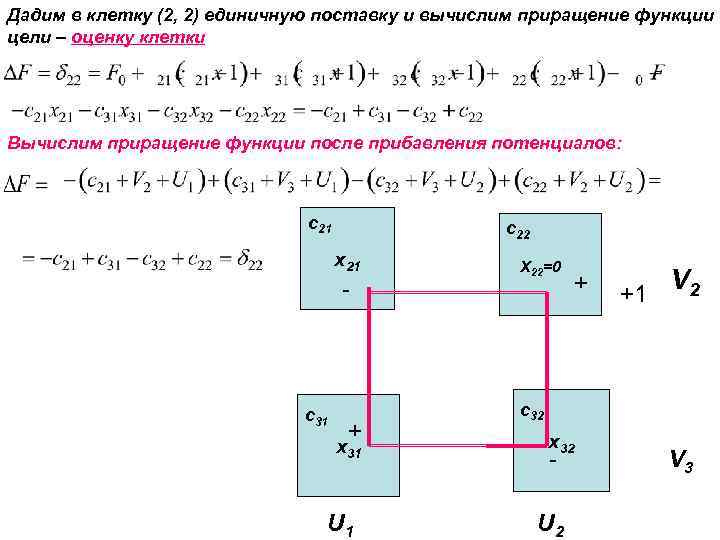Дадим в клетку (2, 2) единичную поставку и вычислим приращение функции цели – оценку клетки Вычислим приращение функции после прибавления потенциалов: c 21 c 22 x 21 - c 31 + x 31 U 1 X 22=0 + +1 V 2 c 32 x 32 - U 2 V 3

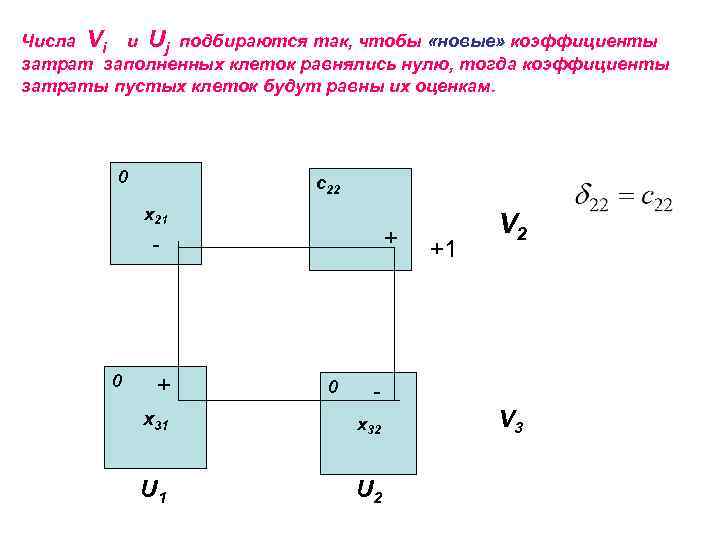Числа Vi и Uj подбираются так, чтобы «новые» коэффициенты затрат заполненных клеток равнялись нулю, тогда коэффициенты затраты пустых клеток будут равны их оценкам. 0 c 22 x 21 + - 0 +1 V 2 - x 31 x 32 U 1 U 2 V 3

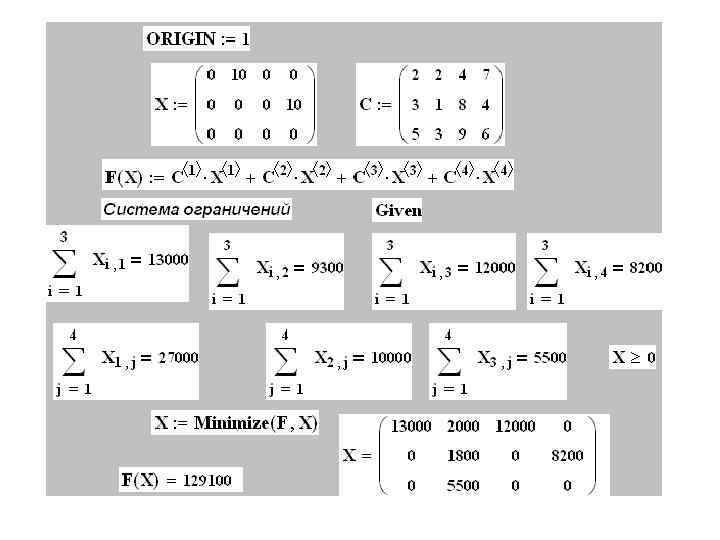
5. Решение транспортной задачи в системе Mathcad. Пример. В хозяйстве имеется 4 участка пастбищ площадью 130, 93, 120, 82 га соответственно. Средняя урожайность на этих пастбищах составляет 100 ц. зеленой массы с 1 га. В этом же хозяйстве есть 3 молочных фермы с потребностью в зеленых кормах 27000, 10000 и 5500 ц соответственно. Необходимо так распределить пастбища между фермами, чтобы суммарные потери молока в стоимостном выражении были минимальными. Исходные данные к задаче приведены в таблице. Замечание. На 1 км перегона коров расходуется столько энергии, сколько необходимо для получения 0, 1 кг молока. Если в день выгон составит 4 км, то за 180 дней при закупочной цене молока 1, 5 рублей за 1 кг потери продукции на 1 корову составят рублей При норме потребления зеленой массы 1 коровой за пастбищный период 54 ц. потери на 1 ц зеленой массы составляют 2 руб (108: 54 =2) С 11=2. Аналогично рассчитываются и другие значения Сij в зависимости от удаленности конкретных пастбищ от ферм.

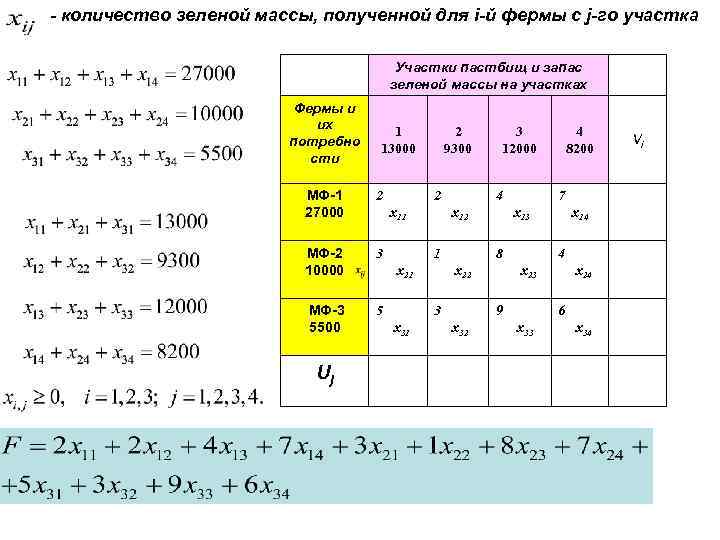- количество зеленой массы, полученной для i-й фермы с j-го участка Участки пастбищ и запас зеленой массы на участках Фермы и их потребно сти 1 13000 МФ-1 27000 2 МФ-2 10000 3 МФ-3 5500 5 Uj 2 9300 2 x 11 4 x 12 1 x 21 x 13 x 22 x 14 4 x 23 9 x 32 4 8200 7 8 3 x 31 3 12000 x 24 6 x 33 x 34 Vi

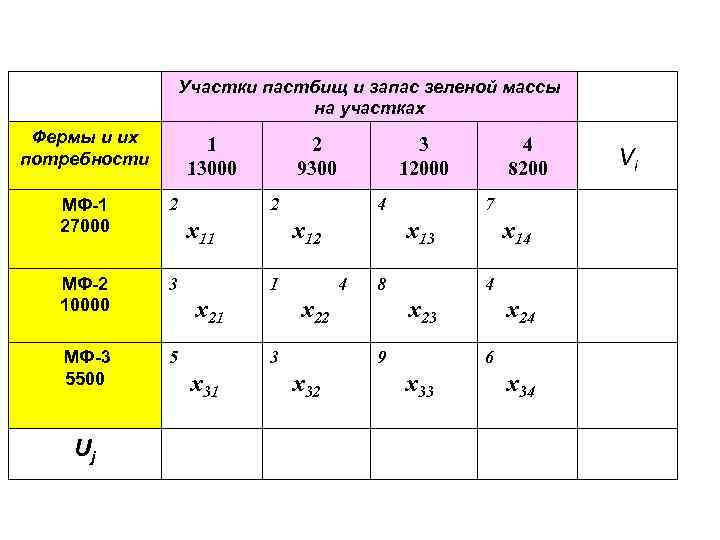Участки пастбищ и запас зеленой массы на участках Фермы и их потребности 1 13000 МФ-1 27000 2 МФ-2 10000 3 МФ-3 5500 5 Uj 2 9300 3 12000 2 x 11 4 x 12 1 x 21 x 31 7 x 13 4 8 x 22 3 x 14 4 x 23 9 x 32 4 8200 x 24 6 x 33 x 34 Vi

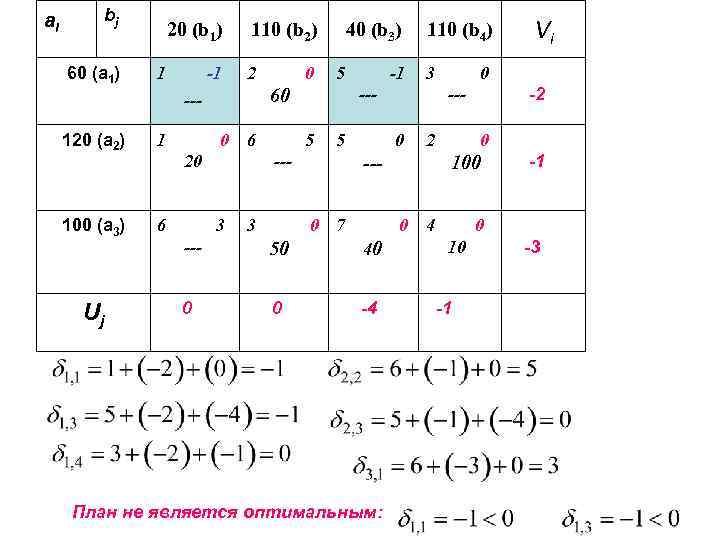ai bj 60 (a 1) 20 (b 1) 1 -1 110 (b 2) 2 1 100 (a 3) 6 Uj 5 0 6 20 5 5 --3 3 -1 110 (b 4) 3 --- 60 --120 (a 2) 0 40 (b 3) 2 --0 7 0 0 100 0 4 --- 50 40 0 0 -4 План не является оптимальным: -2 --0 Vi -1 0 10 -1 -3